4.4: Circular Motion- Linear and Angular Speed
- Page ID
- 3327
Radian measure and arc length can be applied to the study of circular motion. In physics the average speed of an object is defined as:
\[ \text{average speed} ~=~ \frac{\text{distance traveled}}{\text{time elapsed}}
\nonumber \]
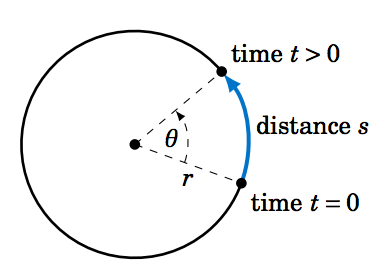
So suppose that an object moves along a circle of radius \(r \), traveling a distance \(s \) over a period of time \(t \), as in Figure 4.4.1. Then it makes sense to define the (average) linear speed \(\nu \) of the object as:
\[ \nu ~=~ \frac{s}{t}\label{eqn:linspeed} \]
Let \(\theta \) be the angle swept out by the object in that period of time. Then we define the (average) angular speed \(\omega \) of the object as:
\[ \omega ~=~ \frac{\theta}{t}\label{eqn:angspeed} \]
Angular speed gives the rate at which the central angle swept out by the object changes as the object moves around the circle, and it is thus measured in radians per unit time. Linear speed is measured in distance units per unit time (e.g. feet per second). The word linear is used because straightening out the arc traveled by the object along the circle results in a line of the same length, so that the usual definition of speed as distance over time can be used. We will usually omit the word average when discussing linear and angular speed here.
Since the length \(s \) of the arc cut off by a central angle \(\theta \) in a circle of radius \(r \) is \(s=r\,\theta \), we see that
\[ \nu ~=~ \frac{s}{t} ~=~ \frac{r\,\theta}{t} ~=~ \frac{\theta}{t} \;\cdot\; r ~,
\nonumber \]
so that we get the following relation between linear and angular speed:
\[ \nu ~=~ \omega\,r\label{eqn:linang} \]
An object sweeps out a central angle of \(\frac{\pi}{3} \) radians in \(0.5 \) seconds as it moves along a circle of radius \(3 \) m. Find its linear and angular speed over that time period.
Solution:
Here we have \(t=0.5 \) sec, \(r=3 \) m, and \(\theta = \frac{\pi}{3} \) rad. So the angular speed \(\omega \) is
\[ \omega ~=~ \frac{\theta}{t} ~=~ \frac{\dfrac{\pi}{3}~\text{rad}}{0.5~\text{sec}}
\quad\Rightarrow\quad \boxed{\omega ~=~ \frac{2\pi}{3}~\text{rad/sec}} ~,
\nonumber \]
and thus the linear speed \(\nu \) is
\[ \nu ~=~ \omega\,r ~=~ \left( \frac{2\pi}{3}~\text{rad/sec} \right) \,(3~\text{m})
\quad\Rightarrow\quad \boxed{\nu ~=~ 2\pi~\text{m/sec}} ~.
\nonumber \] Note that the units for \(\omega \) are rad/sec and the units of \(\nu \) are m/sec. Recall that radians are actually unitless, which is why in the Equation \(\nu=\omega\,r \) the radian units disappear.
An object travels a distance of \(35 \) ft in \(2.7 \) seconds as it moves along a circle of radius \(2 \) ft. Find its linear and angular speed over that time period.
Solution:
Here we have \(t=2.7 \) sec, \(r=2 \) ft, and \(s=35 \) ft. So the linear speed \(\nu \) is
\[ \nu ~=~ \frac{s}{t} ~=~ \frac{35~\text{feet}}{2.7~\text{sec}} \quad\Rightarrow\quad
\boxed{\nu ~=~ 12.96~\text{ft/sec}} ~,
\nonumber \]
and thus the angular speed \(\omega \) is given by
\[ \nonumber
\nu ~=~ \omega\,r \quad\Rightarrow\quad 12.96~\text{ft/sec} ~=~ \omega\,(2~\text{ft})
\quad\Rightarrow\quad \boxed{\omega ~=~ 6.48~\text{rad/sec}} ~.
\nonumber \]
An object moves at a constant linear speed of \(10 \) m/sec around a circle of radius \(4 \) m. How large of a central angle does it sweep out in \(3.1 \) seconds?
Solution:
Here we have \(t=3.1 \) sec, \(\nu=10 \) m/sec, and \(r=4 \) m. Thus, the angle \(\theta \) is given by
\[ s ~=~ r\,\theta \quad\Rightarrow\quad \theta ~=~ \frac{s}{r} ~=~ \frac{\nu\,t}{r} ~=~
\frac{(10~\text{m/sec})\,(3.1~\text{sec})}{4~\text{m}} ~=~ \boxed{7.75~\text{rad}} ~.
\nonumber \]
In many physical applications angular speed is given in revolutions per minute, abbreviated as rpm. To convert from rpm to, say, radians per second, notice that since there are \(2\pi \) radians in one revolution and \(60 \) seconds in one minute, we can convert \(N \) rpm to radians per second by "canceling the units'' as follows:
\[\require{cancel} \nonumber
N~\text{rpm} ~=~ N~\frac{\cancel{\text{rev}}}{\cancel{\text{min}}} \;\cdot\;
\frac{2\pi~\text{rad}}{1~\cancel{\text{rev}}}
\;\cdot\; \frac{1~\cancel{\text{min}}}{60~\text{sec}} ~=~ \frac{N \cdot 2\pi}{60}~\text{rad/sec}
\nonumber \]
This works because all we did was multiply by \(1 \) twice. Converting to other units for angular speed works in a similar way. Going in the opposite direction, say, from rad/sec to rpm, gives:
\[ N~\text{rad/sec} ~=~ \frac{N \cdot 60}{2\pi}~\text{rpm}
\nonumber \]
A gear with an outer radius of \(r_1 = 5 \) cm moves in the clockwise direction, causing an interlocking gear with an outer radius of \(r_2 = 4 \) cm to move in the counterclockwise direction at an angular speed of \(\omega_2 = 25 \) rpm. What is the angular speed \(\omega_1 \) of the larger gear?
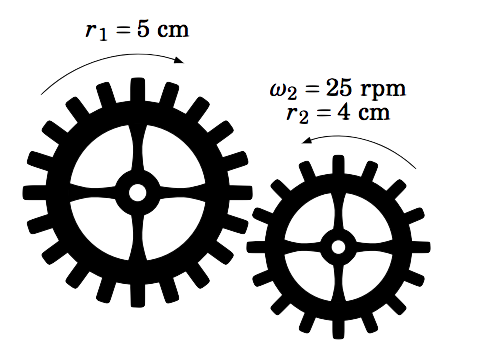
Figure 4.4.2
Solution:
Imagine a particle on the outer radius of each gear. After the gears have rotated for a period of time \(t>0 \), the circular displacement of each particle will be the same. In other words, \(s_1 = s_2 \), where \(s_1 \) and \(s_2 \) are the distances traveled by the particles on the gears with radii \(r_1 \) and \(r_2 \), respectively.
But \(s_1 = \nu_1 \,t \) and \(s_2 = \nu_2 \,t \), where \(\nu_1 \) and \(\nu_2 \) are the linear speeds of the gears with radii \(r_1 \) and \(r_2 \), respectively. Thus,
\[ \nu_1 \,t = \nu_2 \,t \quad\Rightarrow\quad \nu_1 = \nu_2 ~,
\nonumber \]
so by Equation \ref{eqn:linang} we get the fundamental relation between the two gears:
\[
\boxed{\omega_1 \,r_1 ~=~ \omega_2 \,r_2}\label{eqn:gears}
\nonumber \]
Note that this holds for any two gears. So in our case, we have
\[ \omega_1 \,(5) ~=~ (25) \,(4) \quad\Rightarrow\quad \boxed{\omega_1 ~=~ 20~\text{rpm}} ~.
\nonumber \]


