8.E: Further Applications of Trigonometry (Exercises)
- Page ID
- 6013
8.1: Non-right Triangles: Law of Sines
Verbal
1) Describe the altitude of a triangle.
- Answer
-
The altitude extends from any vertex to the opposite side or to the line containing the opposite side at a \(90^{\circ}\) angle.
2) Compare right triangles and oblique triangles.
3) When can you use the Law of Sines to find a missing angle?
- Answer
-
When the known values are the side opposite the missing angle and another side and its opposite angle.
4) In the Law of Sines, what is the relationship between the angle in the numerator and the side in the denominator?
5) What type of triangle results in an ambiguous case?
- Answer
-
A triangle with two given sides and a non-included angle.
Algebraic
For the exercises 6-10, assume \(\alpha\) is opposite side \(a\), \(\beta\) is opposite side \(b\), and \(\gamma\) is opposite side \(c\). Solve each triangle, if possible. Round each answer to the nearest tenth.
6) \(\alpha =43^{\circ}, \gamma =69^{\circ}, a=20\)
7) \(\alpha =35^{\circ}, \gamma =73^{\circ}, c=20\)
- Answer
-
\(\beta =72^{\circ}, a\approx 12.0, b\approx 19.9\)
8) \(\alpha =60^{\circ}, \beta =60^{\circ}, \gamma =60^{\circ}\)
9) \(a=4, \alpha =60^{\circ}, \beta =100^{\circ}\)
- Answer
-
\(\gamma =20^{\circ}, b\approx 4.5, c\approx 1.6\)
10) \(b=10, \beta =95^{\circ}, \gamma =30^{\circ}\)
11) Find side \(b\) when \(A=37^{\circ}, B=49^{\circ}, c=5\)
- Answer
-
\(b\approx 3.78\)
12) Find side \(a\) when \(A=132^{\circ}, C=23^{\circ}, b=10\)
13) Find side \(c\) when \(B=37^{\circ}, C=21^{\circ}, b=23\)
- Answer
-
\(c\approx 13.70\)
For the exercises 14-23, assume \(\alpha \) is opposite side \(a\), \(\beta\) is opposite side \(b\), and \(\gamma \) is opposite side \(c\). Determine whether there is no triangle, one triangle, or two triangles. Then solve each triangle, if possible. Round each answer to the nearest tenth.
14) \(\alpha =119^{\circ}, a=14, b=26\)
15) \(\gamma =113^{\circ}, b=10, c=32\)
- Answer
-
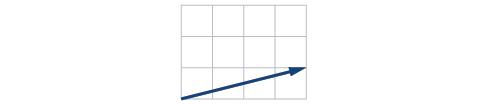
one triangle, \(\alpha \approx 50.3^{\circ}, \beta \approx 16.7^{\circ}, a\approx 26.7\)
16) \(b=3.5, c=5.3, \gamma =80^{\circ}\)
17) \(a=12, c=17, \alpha =35^{\circ}\)
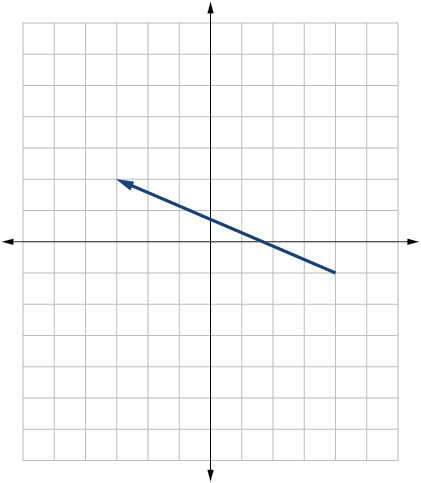
- Answer
-
two triangles, \(\gamma \approx 54.3^{\circ}, \beta \approx 90.7^{\circ}, b\approx 20.9\) or \(\gamma '\approx 125.7^{\circ}, \beta '\approx 19.3^{\circ}, b'\approx 6.9\)
18) \(a=20.5, b=35.0, \beta =25^{\circ}\)
19) \(a=7, c=9, \alpha =43^{\circ}\)
- Answer
-
two triangles, \(\beta \approx 75.7^{\circ}, \gamma \approx 61.3^{\circ}, b\approx 9.9\) or \(\beta '\approx 18.3^{\circ}, \gamma '\approx 118.7^{\circ}, b'\approx 3.2\)
20) \(a=7, b=3, \beta =24^{\circ}\)
21) \(b=13, c=5, \gamma =10^{\circ}\)
- Answer
-
two triangles, \(\alpha \approx 143.2^{\circ}, \beta \approx 26.8^{\circ}, a\approx 17.3\) or \(\alpha '\approx 16.8^{\circ}, \beta '\approx 153.2^{\circ}, a'\approx 8.3\)
22) \(a=2.3, c=1.8, \gamma =28^{\circ}\)
23) \(\beta =119^{\circ}, b=8.2, a=11.3\)
- Answer
-
no triangle possible
For the exercises 24-26, use the Law of Sines to solve, if possible, the missing side or angle for each triangle or triangles in the ambiguous case. Round each answer to the nearest tenth.
24) Find angle \(A\) when \(a=24, b=5, B=22^{\circ}\)
25) Find angle \(A\) when \(a=13, b=6, B=20^{\circ}\)
- Answer
-
\(A\approx 47.8^{\circ}\) or \(A'\approx 132.2^{\circ}\)
26) Find angle \(B\) when \(A=12^{\circ}, a=2, b=9\)
For the exercises 27-30, find the area of the triangle with the given measurements. Round each answer to the nearest tenth.
27) \(a=5, c=6, \beta =35^{\circ}\)
- Answer
-
\(8.6\)
28) \(b=11, c=8, \alpha =28^{\circ}\)
29) \(a=32, b=24, \gamma =75^{\circ}\)
- Answer
-
\(370.9\)
30) \(a=7.2, b=4.5, \gamma =43^{\circ}\)
Graphical
For the exercises 31-36, find the length of side \(x\). Round to the nearest tenth.
31)
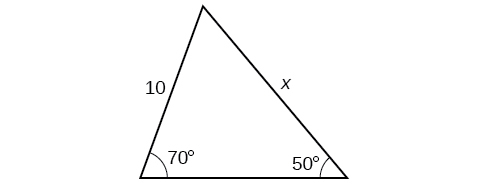
- Answer
-
\(12.3\)
32)
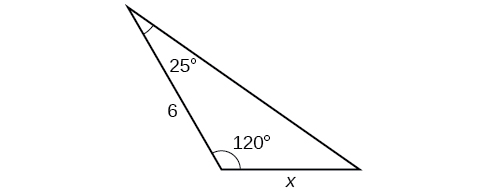
33)

- Answer
-
\(12.2\)
34)
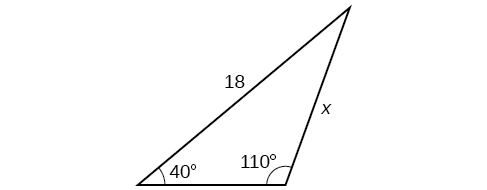
35)
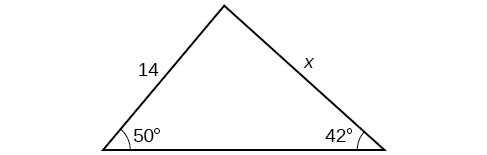
- Answer
-
\(16.0\)
36)
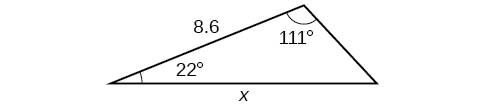
For the exercises 37-,42 find the measure of angle \(x\), if possible. Round to the nearest tenth.
37)
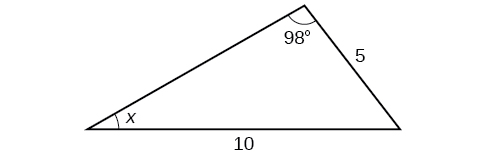
- Answer
-
\(29.7^{\circ}\)
38)
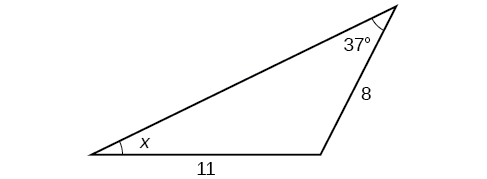
39)
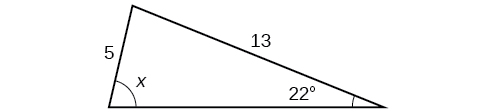
- Answer
-
\(x=76.9^{\circ}\) or \(x=103.1^{\circ}\)
40)
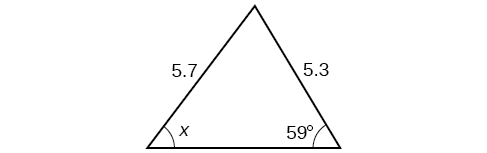
41) Notice that \(x\) is an obtuse angle.
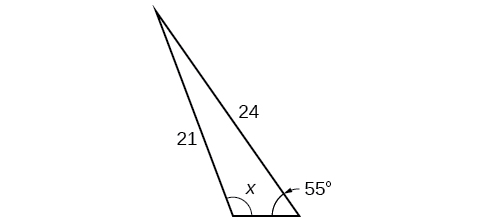
- Answer
-
\(110.6^{\circ}\)
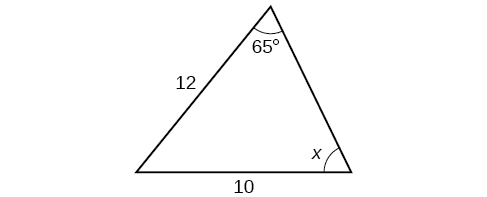
42)
For the exercises 43-49, find the area of each triangle. Round each answer to the nearest tenth.
43)
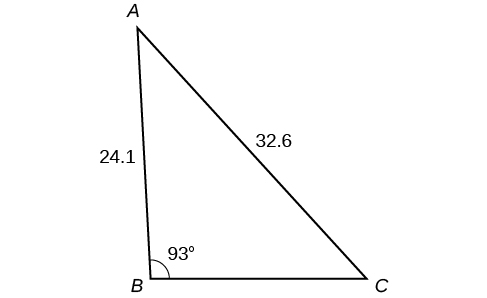
- Answer
-
\(A\approx 39.4, C\approx 47.6, BC\approx 20.7\)
44)
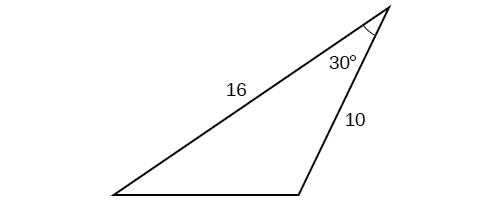
45)
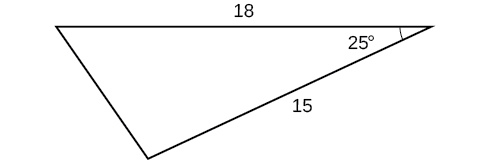
- Answer
-
\(57.1\)
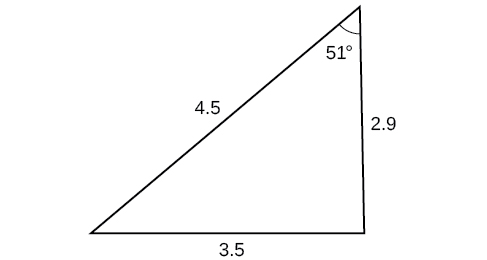
46)
47)
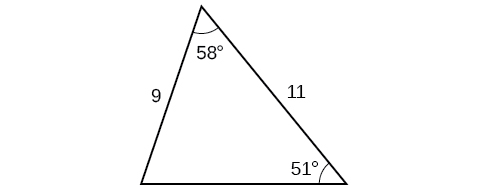
- Answer
-
\(42.0\)
48)
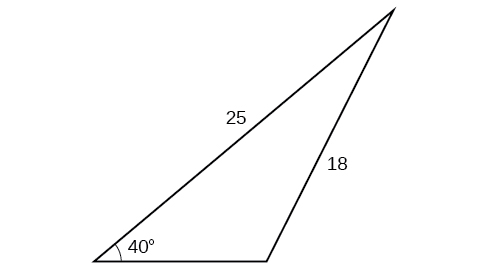
49)
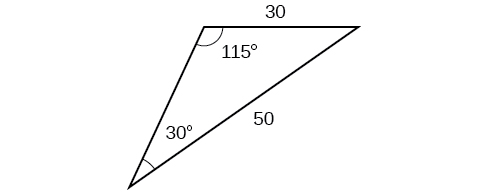
- Answer
-
\(430.2\)
Extensions
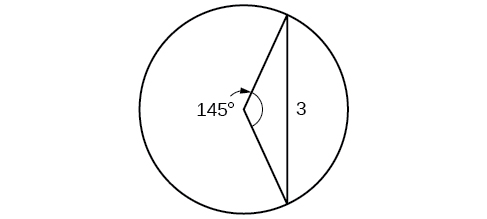
50) Find the radius of the circle in the Figure below. Round to the nearest tenth.
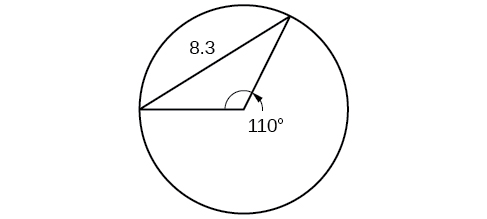
51) Find the diameter of the circle in the Figure below. Round to the nearest tenth.
- Answer
-
\(10.1\)
52) Find \(m\angle ADC\) in the Figure below. Round to the nearest tenth.
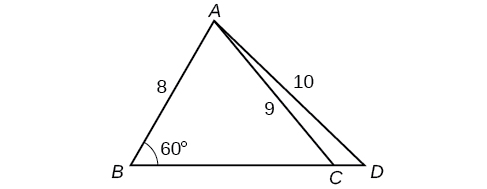
53) Find side \( AD\) in the Figure below. Round to the nearest tenth.
- Answer
-
\(AD\approx 13.8\)
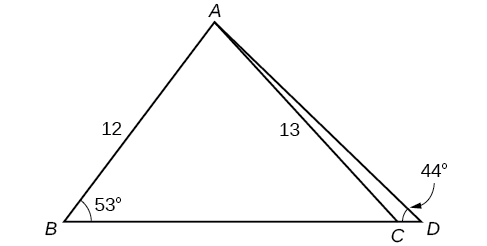
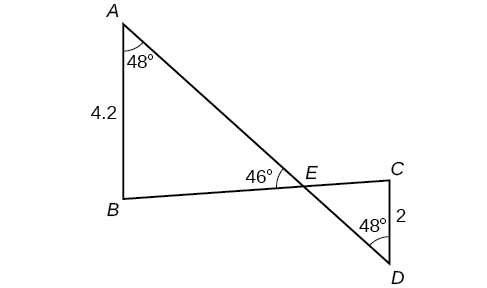
54) Solve both triangles in the Figure below. Round each answer to the nearest tenth.
55) Find side \( AB\) in the parallelogram shown below. Round to the nearest tenth.
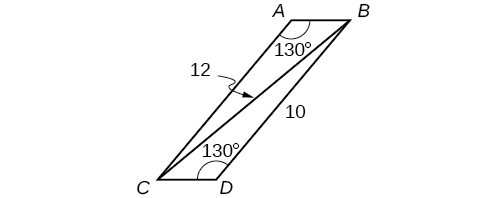
- Answer
-
\(AB\approx 2.8\)
56) Solve the triangle in the Figure below. (Hint: Draw a perpendicular from \(H\) to \(JK\). Round each answer to the nearest tenth.
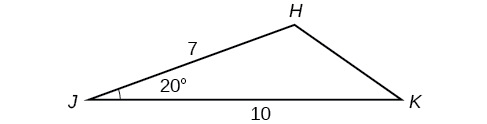
57) Solve the triangle in the Figure below. (Hint: Draw a perpendicular from \(N\) to \(LM\). Round each answer to the nearest tenth.
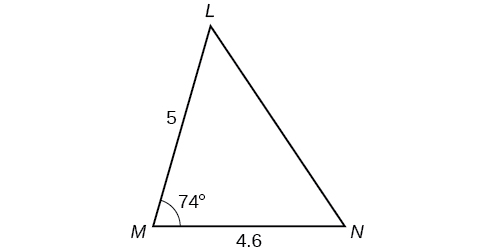
- Answer
-
\(L\approx 49.7 ^{\circ} , N\approx 56.3 ^{\circ} , LN\approx 5.8\)
58) In the Figure below, \(ABCD\) is not a parallelogram. \(\angle m\) is obtuse. Solve both triangles. Round each answer to the nearest tenth.
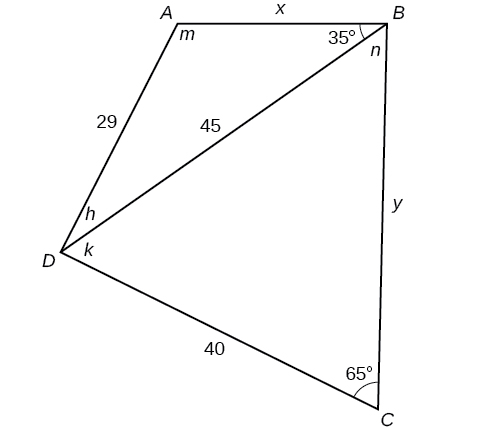
Real-World Applications
59) A pole leans away from the sun at an angle of \(7^{\circ}\) to the vertical, as shown in the Figure below. When the elevation of the sun is \(55^{\circ}\), the pole casts a shadow \(42\) feet long on the level ground. How long is the pole? Round the answer to the nearest tenth.
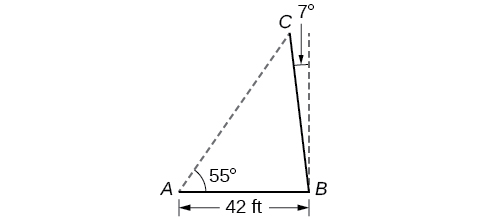
- Answer
-
\(51.4\) ft
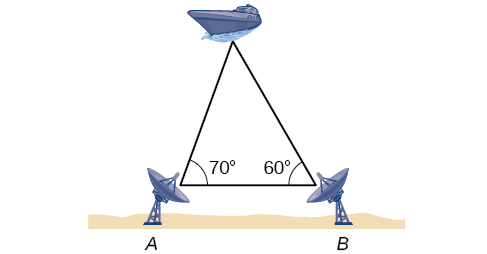
60) To determine how far a boat is from shore, two radar stations \(500\) feet apart find the angles out to the boat, as shown in the Figure below. Determine the distance of the boat from station \(A\) and the distance of the boat from shore. Round your answers to the nearest whole foot.
61) The Figure below shows a satellite orbiting Earth. The satellite passes directly over two tracking stations \(A\) and \(B\), which are \(69\) miles apart. When the satellite is on one side of the two stations, the angles of elevation at \(A\) and \(B\) are measured to be \(86.2^{\circ}\) and \(83.9^{\circ}\) respectively. How far is the satellite from station \(A\) and how high is the satellite above the ground? Round answers to the nearest whole mile.
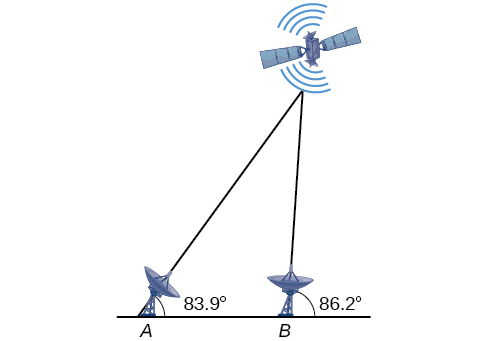
- Answer
-
The distance from the satellite to station \(A\) is approximately \(1716\) miles. The satellite is approximately \(1706\) miles above the ground.
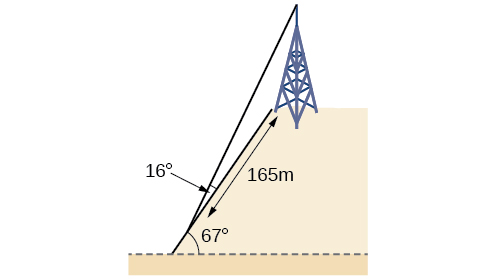
62) A communications tower is located at the top of a steep hill, as shown in the Figure below. The angle of inclination of the hill is \(67^{\circ}\). A guy wire is to be attached to the top of the tower and to the ground, \(165\) meters downhill from the base of the tower. The angle formed by the guy wire and the hill is \(16^{\circ}\). Find the length of the cable required for the guy wire to the nearest whole meter.
63) The roof of a house is at a \(20^{\circ}\) angle. An \(8\)-foot solar panel is to be mounted on the roof and should be angled \(38^{\circ}\) relative to the horizontal for optimal results. (See the Figure below). How long does the vertical support holding up the back of the panel need to be? Round to the nearest tenth.
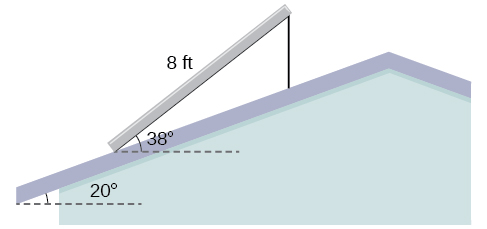
- Answer
-
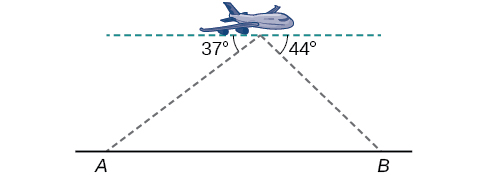
\(2.6\) ft
64) Similar to an angle of elevation, an angle of depression is the acute angle formed by a horizontal line and an observer’s line of sight to an object below the horizontal. A pilot is flying over a straight highway. He determines the angles of depression to two mileposts, \(6.6\) km apart, to be \(37^{\circ}\) and \(44^{\circ}\) as shown in the Figure below. Find the distance of the plane from point \(A\) to the nearest tenth of a kilometer.
65) A pilot is flying over a straight highway. He determines the angles of depression to two mileposts, \(4.3\) km apart, to be \(32^{\circ}\) and \(56^{\circ}\), as shown in the Figure below. Find the distance of the plane from point \(A\) to the nearest tenth of a kilometer.
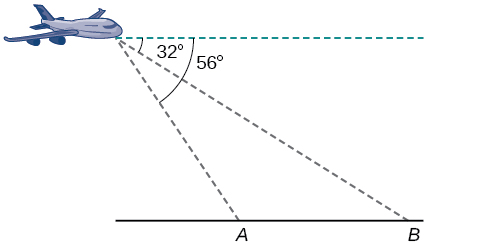
- Answer
-
\(5.6\) km
66) In order to estimate the height of a building, two students stand at a certain distance from the building at street level. From this point, they find the angle of elevation from the street to the top of the building to be \(39^{\circ}\). They then move \(300\) feet closer to the building and find the angle of elevation to be \(50^{\circ}\). Assuming that the street is level, estimate the height of the building to the nearest foot.
67) In order to estimate the height of a building, two students stand at a certain distance from the building at street level. From this point, they find the angle of elevation from the street to the top of the building to be \(35^{\circ}\). They then move \(250\) feet closer to the building and find the angle of elevation to be \(53^{\circ}\). Assuming that the street is level, estimate the height of the building to the nearest foot.
- Answer
-
\(371\) ft
68) Points \(A\) and \(B\) are on opposite sides of a lake. Point \(C\) is \(97\) meters from \(A\). The measure of \(\angle BAC\) is determined to be \(101^{\circ}\), and the measure of \(\angle ACB\) is determined to be \(53^{\circ}\). What is the distance from \(A\) to \(B\)
69) A man and a woman standing \(3\dfrac{1}{2}\) miles apart spot a hot air balloon at the same time. If the angle of elevation from the man to the balloon is \(27^{\circ}\), and the angle of elevation from the woman to the balloon is \(41^{\circ}\), find the altitude of the balloon to the nearest foot.
- Answer
-
\(5936\) ft
70) Two search teams spot a stranded climber on a mountain. The first search team is \(0.5\) miles from the second search team, and both teams are at an altitude of \(1\) mile. The angle of elevation from the first search team to the stranded climber is \(15^{\circ}\). The angle of elevation from the second search team to the climber is \(22^{\circ}\). What is the altitude of the climber? Round to the nearest tenth of a mile.
71) A street light is mounted on a pole. A \(6\)-foot-tall man is standing on the street a short distance from the pole, casting a shadow. The angle of elevation from the tip of the man’s shadow to the top of his head of \(28^{\circ}\). A \(6\)-foot-tall woman is standing on the same street on the opposite side of the pole from the man. The angle of elevation from the tip of her shadow to the top of her head is \(28^{\circ}\). If the man and woman are \(20\) feet apart, how far is the street light from the tip of the shadow of each person? Round the distance to the nearest tenth of a foot.
- Answer
-
\(24.1\) ft
72) Three cities, \(A\), \(B\), and \(C\), are located so that city \(A\) is due east of city \(B\). If city \(C\) is located \(35^{\circ}\) west of north from city \(B\) and is \(100\) miles from city \(A\) and \(70\) miles from city \(B\), how far is city \(A\) from city \(B\)? Round the distance to the nearest tenth of a mile.
73) Two streets meet at an \(80^{\circ}\) angle. At the corner, a park is being built in the shape of a triangle. Find the area of the park if, along one road, the park measures \(180\) feet, and along the other road, the park measures \(215\) feet.
- Answer
-
\(19,056\) ft2
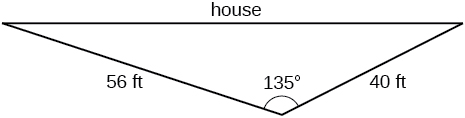
74) Brian’s house is on a corner lot. Find the area of the front yard if the edges measure \(40\) and \(56\) feet, as shown in the Figure below.
75) The Bermuda triangle is a region of the Atlantic Ocean that connects Bermuda, Florida, and Puerto Rico. Find the area of the Bermuda triangle if the distance from Florida to Bermuda is \(1030\) miles, the distance from Puerto Rico to Bermuda is \(980\) miles, and the angle created by the two distances is \(62^{\circ}\).
- Answer
-
\(445,624\) square miles
76) A yield sign measures \(30\) inches on all three sides. What is the area of the sign?
77) Naomi bought a modern dining table whose top is in the shape of a triangle. Find the area of the table top if two of the sides measure \(4\) feet and \(4.5\) feet, and the smaller angles measure \(32^{\circ}\) and \(42^{\circ}\), as shown in the Figure below.
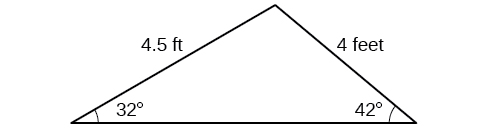
- Answer
-
\(8.65\) ft2
8.2: Non-right Triangles - Law of Cosines
Verbal
1) If you are looking for a missing side of a triangle, what do you need to know when using the Law of Cosines?
- Answer
-
two sides and the angle opposite the missing side.
2) If you are looking for a missing angle of a triangle, what do you need to know when using the Law of Cosines?
3) Explain what \(s\) represents in Heron’s formula.
- Answer
-
\(s\) is the semi-perimeter, which is half the perimeter of the triangle.
4) Explain the relationship between the Pythagorean Theorem and the Law of Cosines.
5) When must you use the Law of Cosines instead of the Pythagorean Theorem?
- Answer
-
The Law of Cosines must be used for any oblique (non-right) triangle.
Algebraic
For the exercises 6-15, assume \(\alpha \) is opposite side \(a\), \(\beta \) is opposite side \(b\), and \(\gamma \) is opposite side \(c\). If possible, solve each triangle for the unknown side. Round to the nearest tenth.
6) \(\gamma =41.2^{\circ}, a=2.49, b=3.13\)
7) \(\alpha =120^{\circ}, b=6, c=7\)
- Answer
-
\(11.3\)
8) \(\beta =58.7^{\circ}, a=10.6, c=15.7\)
9) \(\alpha =115^{\circ}, a=18, b=23\)
- Answer
-
\(34.7\)
10) \(\alpha =119^{\circ}, a=26, b=14\)
11) \(\gamma =113^{\circ}, b=10, c=32\)
- Answer
-
\(26.7\)
12) \(\beta =67^{\circ}, a=49, b=38\)
13) \(\alpha =43.1^{\circ}, a=184.2, b=242.8\)
- Answer
-
\(257.4\)
14) \(\alpha =36.6^{\circ}, a=186.2, b=242.2\)
15) \(\beta =50^{\circ}, a=105, b=45\)
- Answer
-
not possible
For the exercises 16-20, use the Law of Cosines to solve for the missing angle of the oblique triangle. Round to the nearest tenth.
16) \(a=42, b=19, c=30\); find angle \(A\).
17) \(a=14, b=13, c=20\); find angle \(C\).
- Answer
-
\(95.5^{\circ}\)
18) \(a=16, b=31, c=20\); find angle \(B\).
19) \(a=13, b=22, c=28\); find angle \(A\).
- Answer
-
\(26.9^{\circ}\)
20) \(a=108, b=132, c=160\); find angle \(C\).
For the exercises 21-26, solve the triangle. Round to the nearest tenth.
21) \(A=35^{\circ}, b=8, c=11\)
- Answer
-
\(B\approx 45.9^{\circ}, C\approx 99.1^{\circ}, a\approx 6.4\)
22) \(B=88^{\circ}, a=4.4, c=5.2\)
23) \(C=121^{\circ}, a=21, b=37\)
- Answer
-
\(A\approx 20.6^{\circ}, B\approx 38.4^{\circ}, c\approx 51.1\)
24) \(a=13, b=11, c=15\)
25) \(a=3.1, b=3.5, c=5\)
- Answer
-
\(A\approx 37.8^{\circ}, B\approx 43.8^{\circ}, C\approx 98.4\)
26) \(a=51, b=25, c=29\)
For the exercises 27-,31 use Heron’s formula to find the area of the triangle. Round to the nearest hundredth.
27) Find the area of a triangle with sides of length \(18\) in, \(21\) in, and \(32\) in. Round to the nearest tenth.
- Answer
-
\(177.56\) in2
28) Find the area of a triangle with sides of length \(20\) cm, \(26\) cm, and \(37\) cm. Round to the nearest tenth.
29) \(a=\dfrac{1}{2}\) m, \(b=\dfrac{1}{3}\) m, \(c=\dfrac{1}{4}\) m
- Answer
-
\(0.04\) m2
30) \(a=12.4\) ft, \(b=13.7\) ft, \(c=20.2\) ft
31) \(a=1.6\) yd, \(b=2.6\) yd, \(c=4.1\) yd
- Answer
-
\(0.91\) yd2
Graphical
For the exercises 32-37, find the length of side \(x\). Round to the nearest tenth.
32)
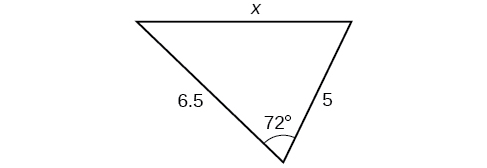
33)
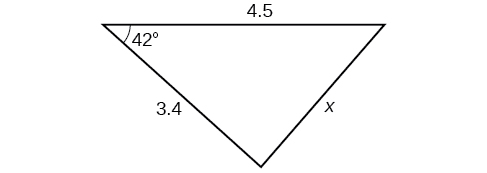
- Answer
-
\(3.0\)
34)
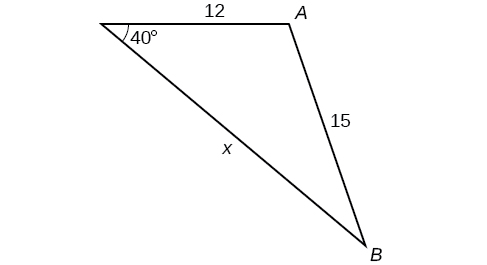
35)
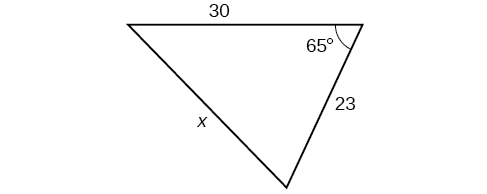
- Answer
-
\(29.1\)
36)
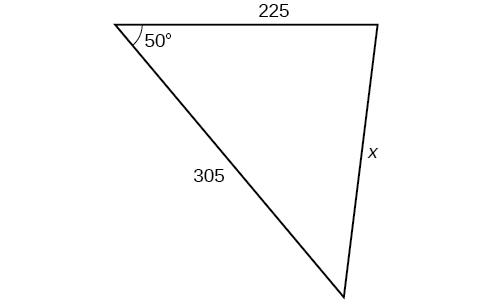
37)
- Answer
-
\(0.5\)
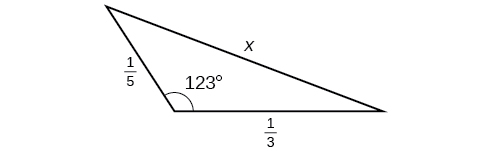
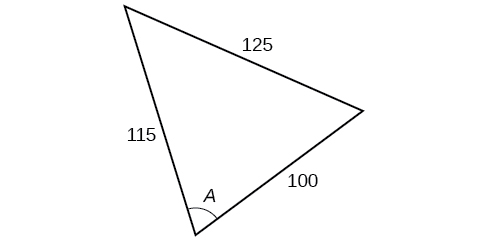
For the exercises 38-41, find the measurement of angle \(A\)
38)
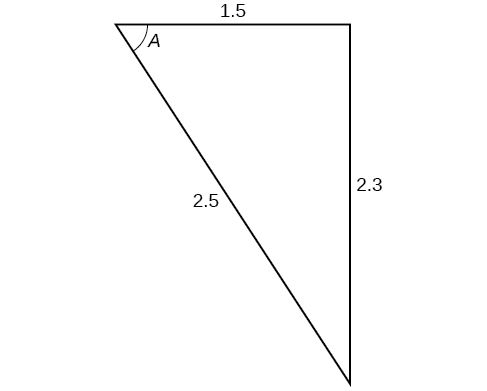
39)
- Answer
-
\(70.7^{\circ}\)
40)
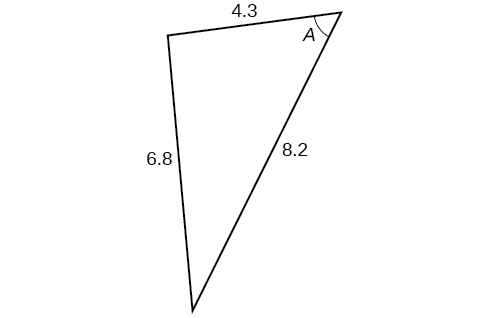
41)
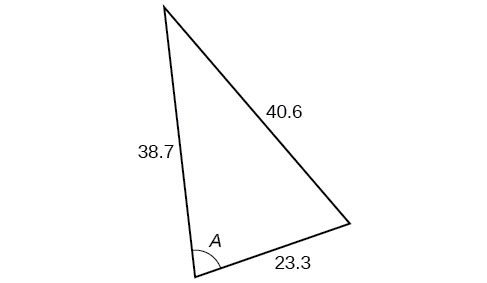
- Answer
-
\(77.4^{\circ}\)
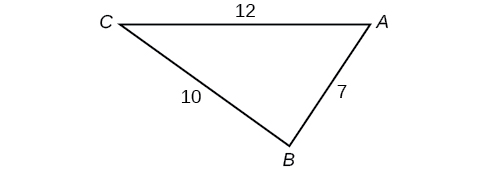
42) Find the measure of each angle in the triangle shown in the Figure below. Round to the nearest tenth.
For the exercises 43-46, solve for the unknown side. Round to the nearest tenth.
43)
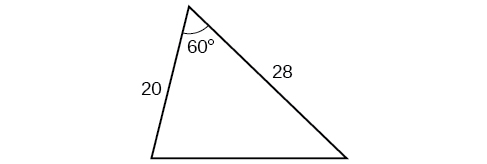
- Answer
-
\(25.0\)
44)
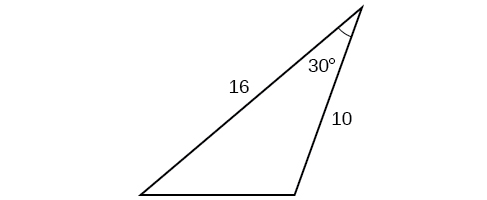
45)
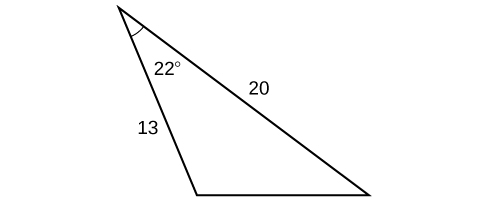
- Answer
-
\(9.3\)
46)
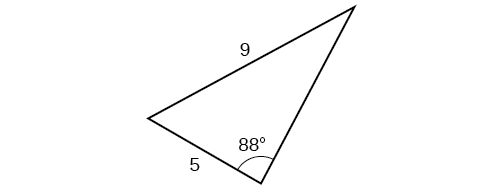
For the exercises 47-51, find the area of the triangle. Round to the nearest hundredth.
47)
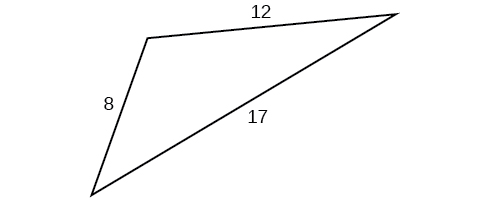
- Answer
-
\(43.52\)
48)
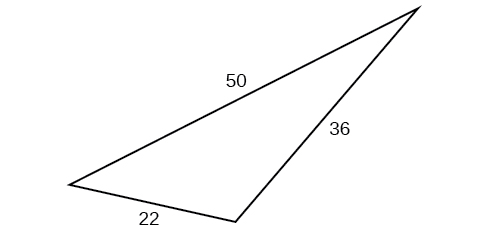
49)
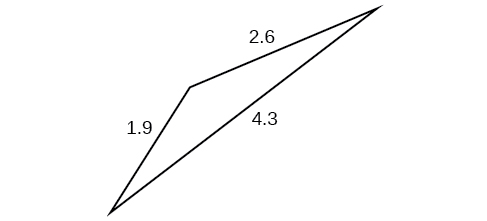
- Answer
-
\(1.41\)
50)
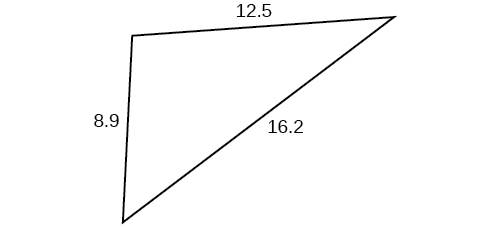
51)
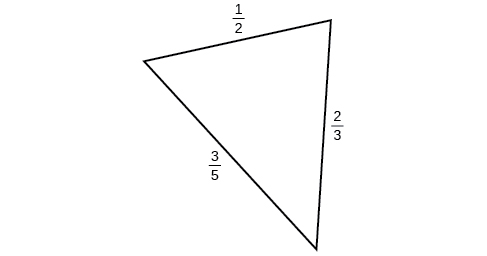
- Answer
-
\(0.14\)
Extensions
52) A parallelogram has sides of length \(16\) units and \(10\) units. The shorter diagonal is \(12\) units. Find the measure of the longer diagonal.
53) The sides of a parallelogram are \(11\) feet and \(17\) feet. The longer diagonal is \(22\) feet. Find the length of the shorter diagonal.
- Answer
-
\(18.3\)
54) The sides of a parallelogram are \(28\) centimeters and \(40\) centimeters. The measure of the larger angle is\(100^{\circ}\). Find the length of the shorter diagonal.
55) A regular octagon is inscribed in a circle with a radius of \(8\) inches. (See Figure below.) Find the perimeter of the octagon.
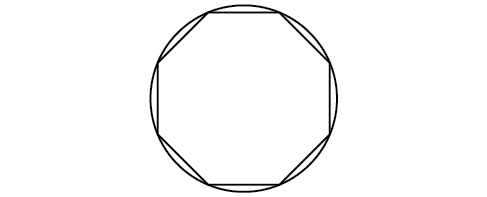
- Answer
-
\(48.98\)
56) A regular pentagon is inscribed in a circle of radius \(12\) cm. (See Figure below.) Find the perimeter of the pentagon. Round to the nearest tenth of a centimeter.

For the exercises 57-58, suppose that \(x^2=25+36-60\cos(52)\) represents the relationship of three sides of a triangle and the cosine of an angle.
57) Draw the triangle.
- Answer
-
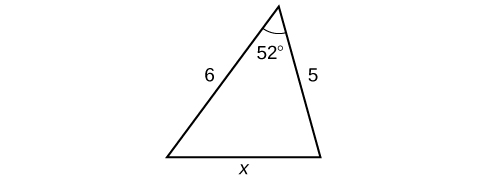
58) Find the length of the third side.
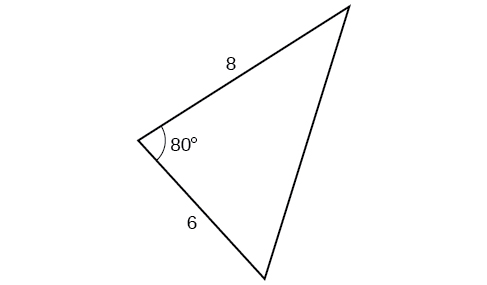
For the exercises 59-61, find the area of the triangle.
59)

- Answer
-
\(7.62\)
60)
61)
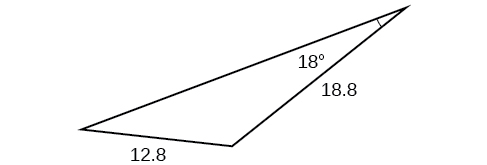
- Answer
-
\(85.1\)
Real-World Applications
62) A surveyor has taken the measurements shown in the Figure below. Find the distance across the lake. Round answers to the nearest tenth.
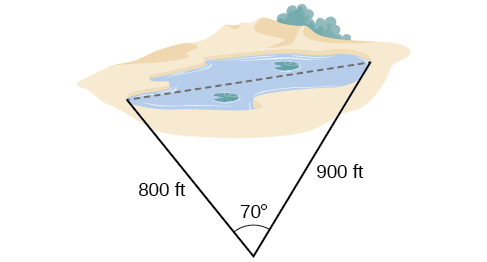
- Answer
-
\(24.0\) km
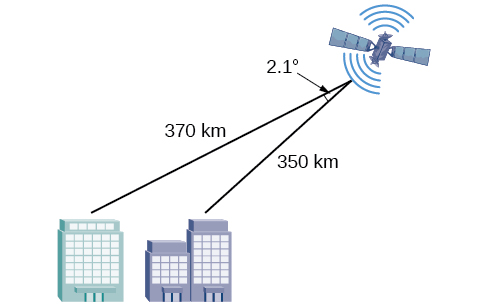
64) An airplane flies \(220\) miles with a heading of \(40^{\circ}\), and then flies \(180\) miles with a heading of \(170^{\circ}\). How far is the plane from its starting point, and at what heading? Round answers to the nearest tenth.
65) A \(113\)-foot tower is located on a hill that is inclined \(34^{\circ}\) to the horizontal, as shown in the Figure below. A guy-wire is to be attached to the top of the tower and anchored at a point \(98\) feet uphill from the base of the tower. Find the length of wire needed.
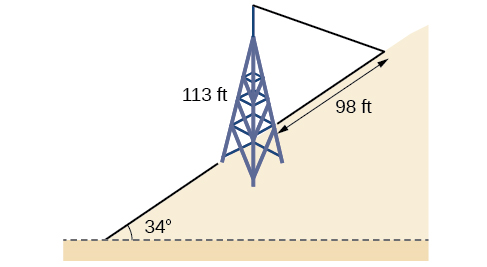
- Answer
-
\(99.9\) ft
66) Two ships left a port at the same time. One ship traveled at a speed of \(18\) miles per hour at a heading of \(320^{\circ}\). The other ship traveled at a speed of \(22\) miles per hour at a heading of \(194^{\circ}\). Find the distance between the two ships after \(10\) hours of travel.
67) The graph in the Figure below represents two boats departing at the same time from the same dock. The first boat is traveling at \(18\) miles per hour at a heading of \(327^{\circ}\) and the second boat is traveling at \(4\) miles per hour at a heading of \(60^{\circ}\). Find the distance between the two boats after \(2\) hours.
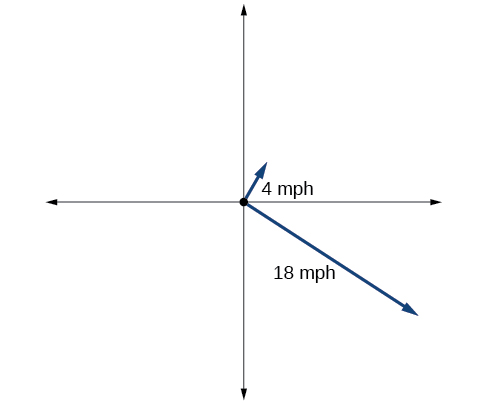
- Answer
-
\(37.3\) miles
68) A triangular swimming pool measures \(40\) feet on one side and \(65\) feet on another side. These sides form an angle that measures \(50^{\circ}\). How long is the third side (to the nearest tenth)?
69) A pilot flies in a straight path for \(1\) hour \(30\) min. She then makes a course correction, heading \(10^{\circ}\) to the right of her original course, and flies \(2\) hours in the new direction. If she maintains a constant speed of \(680\) miles per hour, how far is she from her starting position?
- Answer
-
\(2371\) miles
70) Los Angeles is \(1,744\) miles from Chicago, Chicago is \(714\) miles from New York, and New York is \(2,451\) miles from Los Angeles. Draw a triangle connecting these three cities, and find the angles in the triangle.
71) Philadelphia is \(140\) miles from Washington, D.C., Washington, D.C. is \(442\) miles from Boston, and Boston is \(315\) miles from Philadelphia. Draw a triangle connecting these three cities and find the angles in the triangle.
- Answer
-
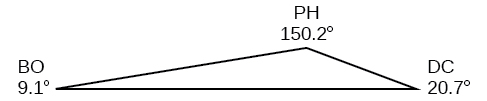
72) Two planes leave the same airport at the same time. One flies at \(20^{\circ}\) east of north at \(500\) miles per hour. The second flies at \(30^{\circ}\) east of south at \(600\) miles per hour. How far apart are the planes after \(2\) hours?
73) Two airplanes take off in different directions. One travels \(300\) mph due west and the other travels \(25^{\circ}\) north of west at \(420\) mph. After \(90\) minutes, how far apart are they, assuming they are flying at the same altitude?
- Answer
-
\(599.8\) miles
74) A parallelogram has sides of length \(15.4\) units and \(9.8\) units. Its area is \(72.9\) square units. Find the measure of the longer diagonal.
75) The four sequential sides of a quadrilateral have lengths \(4.5\) cm, \(7.9\) cm, \(9.4\) cm, and \(12.9\) cm. The angle between the two smallest sides is \(117^{\circ}\). What is the area of this quadrilateral?
- Answer
-
\(65.4\) cm2
76) The four sequential sides of a quadrilateral have lengths \(5.7\) cm, \(7.2\) cm, \(9.4\) cm, and \(12.8\) cm. The angle between the two smallest sides is \(106^{\circ}\). What is the area of this quadrilateral?
77) Find the area of a triangular piece of land that measures \(30\) feet on one side and \(42\) feet on another; the included angle measures \(132^{\circ}\). Round to the nearest whole square foot.
- Answer
-
\(468\) ft2
78) Find the area of a triangular piece of land that measures \(110\) feet on one side and \(250\) feet on another; the included angle measures \(85^{\circ}\). Round to the nearest whole square foot.
8.3: Polar Coordinates
Verbal
1) How are polar coordinates different from rectangular coordinates?
- Answer
-
For polar coordinates, the point in the plane depends on the angle from the positive \(x\)-axis and distance from the origin, while in Cartesian coordinates, the point represents the horizontal and vertical distances from the origin. For each point in the coordinate plane, there is one representation, but for each point in the polar plane, there are infinite representations
2) How are the polar axes different from the \(x\)- and \(y\)-axes of the Cartesian plane?
3) Explain how polar coordinates are graphed.
- Answer
-
Determine \(\theta \) for the point, then move \(r\) units from the pole to plot the point. If \(r\) is negative, move \(r\) units from the pole in the opposite direction but along the same angle. The point is a distance of \(r\) away from the origin at an angle of \(\theta \) from the polar axis.
4) How are the points \(\left ( 3,\dfrac{\pi }{2} \right )\) and \(\left ( -3,\dfrac{\pi }{2} \right )\) related?
5) Explain why the points \(\left ( -3,\dfrac{\pi }{2} \right )\) and \(\left ( 3,-\dfrac{\pi }{2} \right )\) are the same.
- Answer
-
The point \(\left ( -3,\dfrac{\pi }{2} \right )\) has a positive angle but a negative radius and is plotted by moving to an angle of \(\dfrac{\pi }{2}\) and then moving \(3\) units in the negative direction. This places the point \(3\) units down the negative \(y\)-axis. The point \(\left ( 3,-\dfrac{\pi }{2} \right )\) has a negative angle and a positive radius and is plotted by first moving to an angle of \(-\dfrac{\pi }{2}\) and then moving \(3\) units down, which is the positive direction for a negative angle. The point is also \(3\) units down the negative \(y\)-axis.
Algebraic
6) \(\left ( 7,\dfrac{7\pi }{6} \right )\)
7) \((5,\pi )\)
- Answer
-
\((-5,0)\)
8) \(\left ( 6,-\dfrac{\pi }{4} \right )\)
9) \(\left ( -3,\dfrac{\pi }{6} \right )\)
- Answer
-
\(\left ( -\dfrac{3\sqrt{3}}{2},-\dfrac{3}{2} \right )\)
10) \(\left ( 4,\dfrac{7\pi }{4} \right )\)
For the exercises 11-15, convert the given Cartesian coordinates to polar coordinates with \(r>0\) and \(0\leq \theta \leq 2\pi\). Remember to consider the quadrant in which the given point is located.
11) \((4,2)\)
- Answer
-
\((2\sqrt{5},0.464)\)
12) \((-4,6)\)
13) \((3,-5)\)
- Answer
-
\((\sqrt{34},5.253)\)
14) \((-10,-13)\)
15) \((8,8)\)
- Answer
-
\(\left(8\sqrt{2},\dfrac{\pi }{4}\right)\)
For the exercises 16-27, convert the given Cartesian equation to a polar equation.
16) \(x=3\)
17) \(y=4\)
- Answer
-
\(r=4\csc \theta \)
18) \(y=4x^2\)
19) \(y=2x^4\)
- Answer
-
\(r=\sqrt[3]{\dfrac{\sin \theta }{2\cos ^4\theta }}\)
20) \(x^2 + y^2 = 4y\)
21) \(x^2 + y^2 = 3x\)
- Answer
-
\(r=3\cos \theta \)
22) \(x^2 - y^2 = x\)
23) \(x^2 - y^2 = 3y\)
- Answer
-
\(r=\dfrac{3\sin \theta }{\cos (2\theta )}\)
24) \(x^2 + y^2 = 9\)
25) \(x^2 = 9y\)
- Answer
-
\(r=\dfrac{9\sin \theta }{\cos ^2\theta }\)
26) \(y^2 = 9x\)
27) \(9xy = 1\)
- Answer
-
\(r=\sqrt{\dfrac{1}{9\cos \theta \sin \theta }}\)
For the exercises 28-39, convert the given polar equation to a Cartesian equation. Write in the standard form of a conic if possible, and identify the conic section represented.
28) \(r=3\sin \theta\)
29) \(r=4\cos \theta\)
- Answer
-
\(x^2 + y^2 =4x\) or \(\dfrac{(x-2)^2}{4} + \dfrac{y^2}{4} = 1\); circle
30) \(r = \dfrac{4}{\sin \theta +7\cos \theta }\)
31) \(r = \dfrac{6}{\cos \theta +3\sin \theta }\)
- Answer
-
\(3y+x=6\); line
32) \(r=2\sec \theta\)
33) \(r=3\csc \theta\)
- Answer
-
\(y=3\); line
34) \(r = \sqrt{r\cos \theta +2}\)
35) \(r^2 = 4\sec \theta \csc \theta\)
- Answer
-
\(xy=4\); hyperbola
36) \(r =4\)
37) \(r^2 = 4\)
- Answer
-
\(x^2 + y^2 =4\); circle
38) \(r = \dfrac{1}{4\cos \theta - 3\sin \theta }\)
39) \(r = \dfrac{3}{\cos \theta - 5\sin \theta }\)
- Answer
-
\(x-5y=3\); line
Graphical
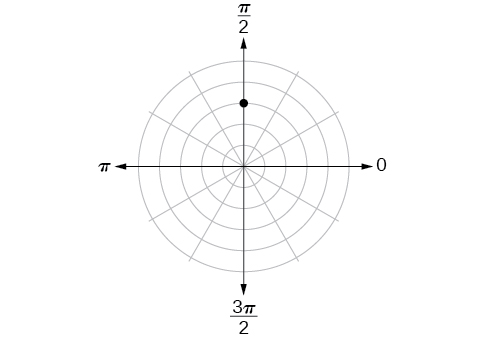
For the exercises 40-44, find the polar coordinates of the point.
40)
41)
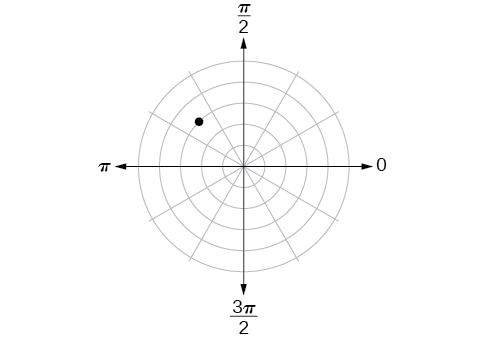
- Answer
-
\(\left (3,\dfrac{3\pi }{4} \right )\)
42)
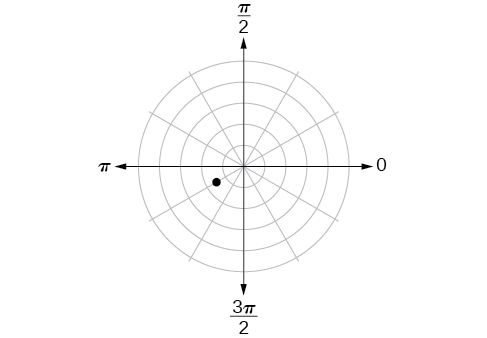
43)
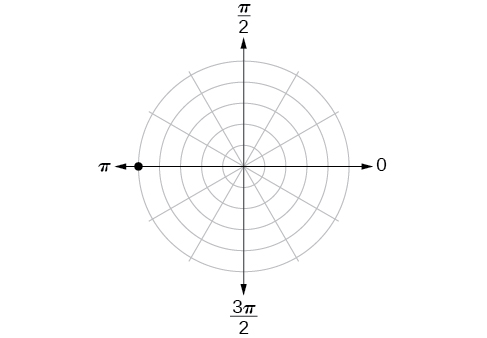
- Answer
-
\((5,\pi )\)
44)
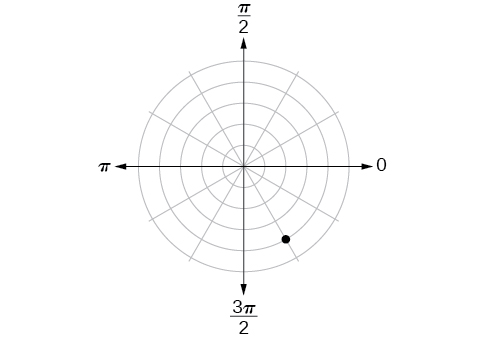
For the exercises 45-54, plot the points.
45) \(\left (-2,\dfrac{\pi }{3} \right )\)
- Answer
-
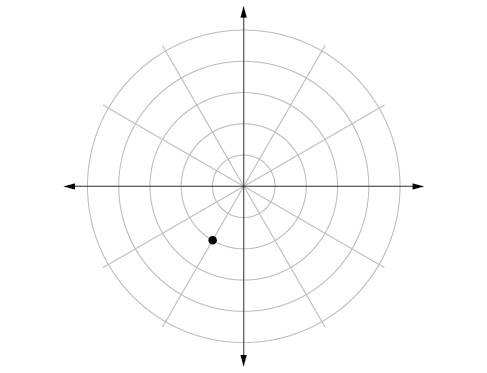
46) \(\left (-1,-\dfrac{\pi }{2} \right )\)
47) \(\left (3.5,\dfrac{7\pi }{4} \right )\)
- Answer
-
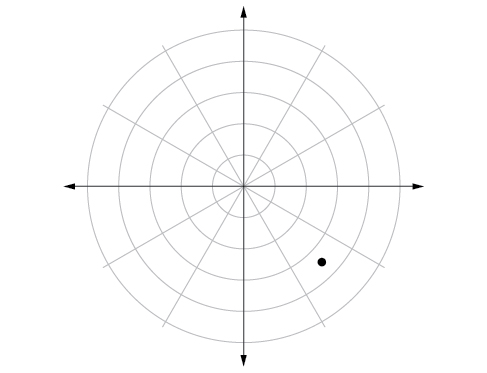
48) \(\left (-4,\dfrac{\pi }{3} \right )\)
49) \(\left (5,\dfrac{\pi }{2} \right )\)
- Answer
-
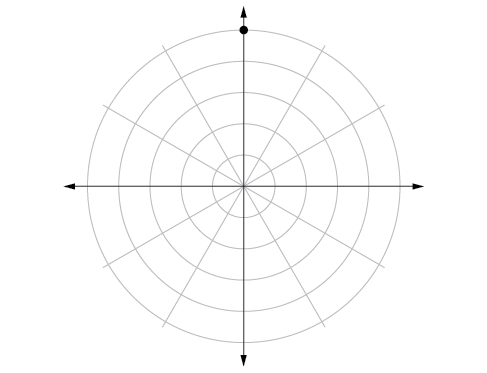
50) \(\left (4,\dfrac{-5\pi }{4} \right )\)
51) \(\left (3,\dfrac{5\pi }{6} \right )\)
- Answer
-
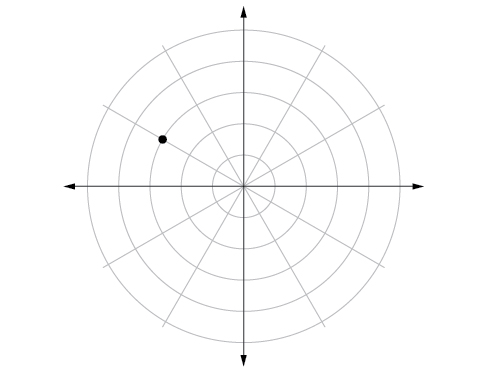
52) \(\left (-1.5,\dfrac{7\pi }{6} \right )\)
53) \(\left (-2,\dfrac{\pi }{4} \right )\)
- Answer
-
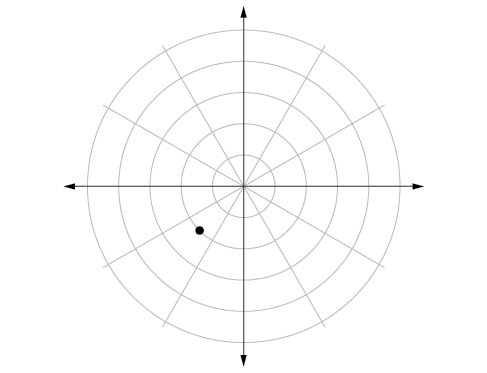
54) \(\left (1,\dfrac{3\pi }{2} \right )\)
For the exercises 55-61, convert the equation from rectangular to polar form and graph on the polar axis.
55) \(5x-y = 6\)
- Answer
-
\(r = \dfrac{6}{5\cos \theta - \sin \theta }\)
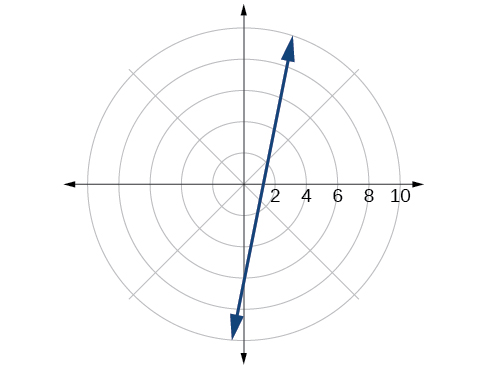
56) \(2x + 7y = -3\)
57) \(x^2 + (y-1)^2 = 1\)
- Answer
-
\(r = 2\sin \theta \)
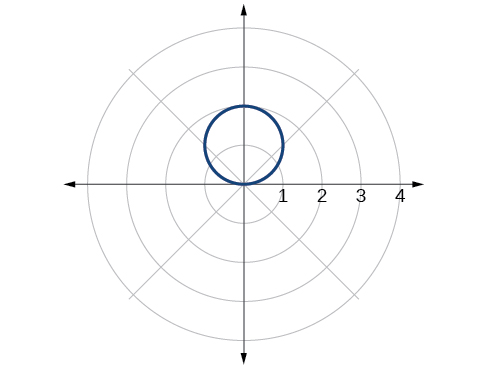
58) \((x+2)^2+(y+3)^2=13\)
59) \(x = 2\)
- Answer
-
\(r = \dfrac{2}{\cos \theta }\)
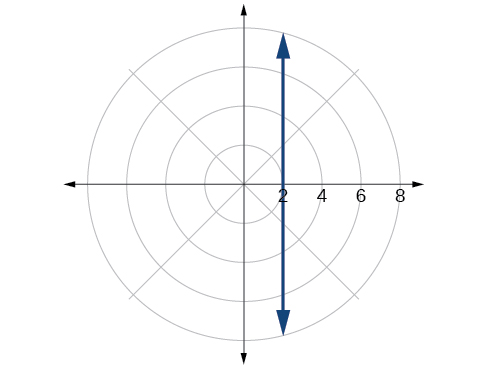
60) \(x^2 + y^2 =5y\)
61) \(x^2 + y^2 =3x\)
- Answer
-
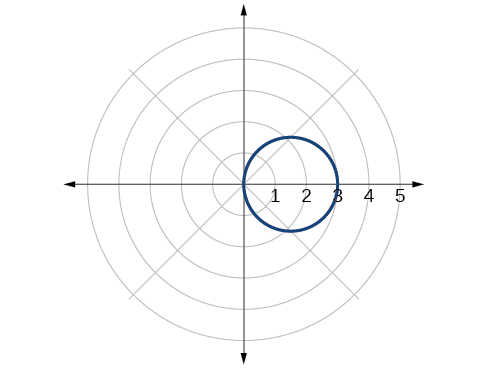
\(r = 3\cos \theta \)
For the exercises 62-68, convert the equation from polar to rectangular form and graph on the rectangular plane.
62) \(r = 6\)
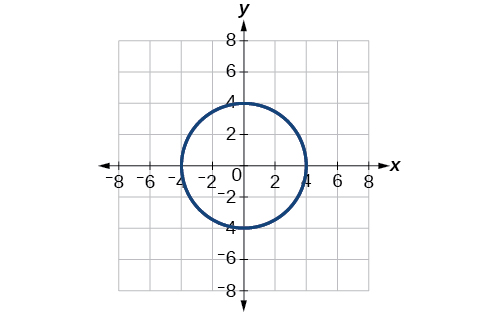
63) \(r = -4\)
- Answer
-
\(x^2 + y^2 =16\)
64) \(\theta = -\dfrac{2\pi }{3}\)
65) \(\theta = \dfrac{\pi }{4}\)
- Answer
-
\(y=x\)
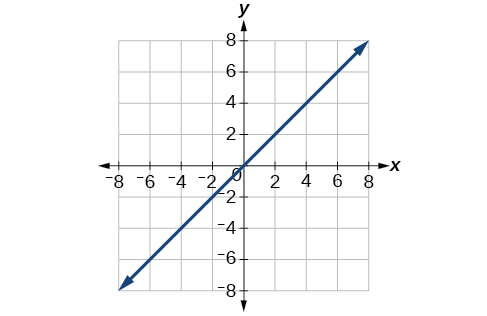
66) \(r = \sec \theta \)
67) \(r = -10\sin \theta \)
- Answer
-
\(x^2 + (y+5)^2 = 25\)
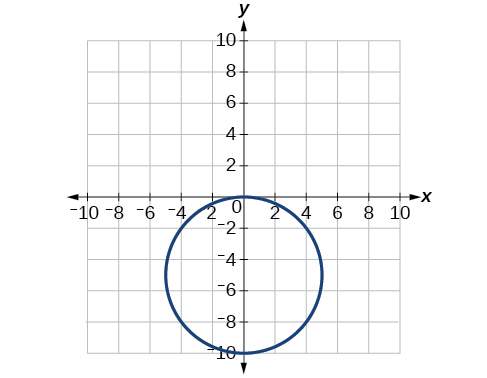
68) \(r = 3\cos \theta \)
Technology
69) Use a graphing calculator to find the rectangular coordinates of \(\left (2,-\dfrac{\pi }{5} \right )\)
- Answer
-
\((1.618,-1.176)\)
70) Use a graphing calculator to find the rectangular coordinates of \(\left (-3,\dfrac{3\pi }{7} \right )\). Round to the nearest thousandth.
71) Use a graphing calculator to find the polar coordinates of \((-7,8)\) in degrees. Round to the nearest thousandth.
- Answer
-
\((10.630,131.186^{\circ})\)
72) Use a graphing calculator to find the polar coordinates of \((3,-4)\) in degrees. Round to the nearest hundredth.
73) Use a graphing calculator to find the polar coordinates of \((-2,0)\) in degrees. Round to the nearest hundredth.
- Answer
-
\((2,3.14)\) or \((2,\pi )\)
Extensions
74) Describe the graph of \(r=a\sec \theta \); \(a>0\).
75) Describe the graph of \(r=a\sec \theta \); \(a<0\).
- Answer
-
A vertical line with \(a\) units left of the \(y\)-axis.
76) Describe the graph of \(r=a\csc \theta \); \(a>0\).
77) Describe the graph of \(r=a\csc \theta \); \(a<0\).
- Answer
-
A horizontal line with \(a\) units below the \(x\)-axis.
78) What polar equations will give an oblique line?
For the exercises 79-84, graph the polar inequality.
79) \(r<4\)
- Answer
-
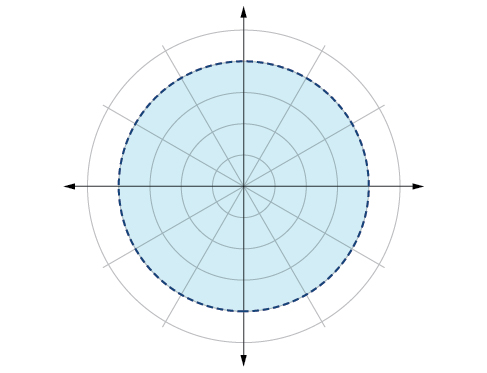
80) \(0\leq \theta \leq \dfrac{\pi }{4}\)
81) \(\theta = \dfrac{\pi }{4}, r\geq 2\)
- Answer
-
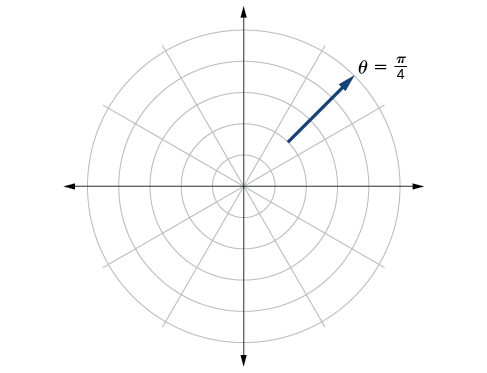
82) \(\theta = \dfrac{\pi }{4}, r\geq -3\)
83) \(0\leq \theta \leq \dfrac{\pi }{3}, r<2\)
- Answer
-
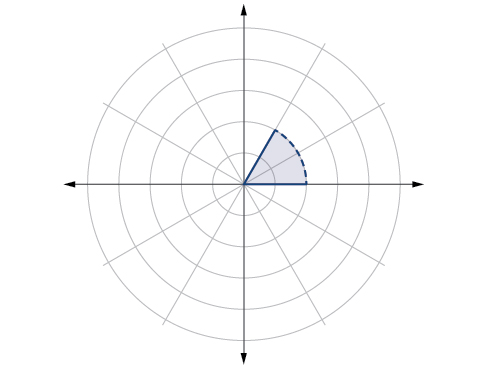
84) \(\dfrac{-\pi }{6} < \theta \leq \dfrac{\pi }{3}, -3<r<2\)
8.4: Polar Coordinates - Graphs
Verbal
1) Describe the three types of symmetry in polar graphs, and compare them to the symmetry of the Cartesian plane.
- Answer
-
Symmetry with respect to the polar axis is similar to symmetry about the \(x\)-axis, symmetry with respect to the pole is similar to symmetry about the origin, and symmetric with respect to the line \(\theta = \dfrac{\pi }{2}\) is similar to symmetry about the \(y\)-axis.
2) Which of the three types of symmetries for polar graphs correspond to the symmetries with respect to the \(x\)-axis, \(y\)-axis, and origin?
3) What are the steps to follow when graphing polar equations?
- Answer
-
Test for symmetry; find zeros, intercepts, and maxima; make a table of values. Decide the general type of graph, cardioid, limaçon, lemniscate, etc., then plot points at \(\theta = 0\), \(\dfrac{\pi }{2}\), \(\pi \), and \(\dfrac{3\pi }{2}\) and sketch the graph.
4) Describe the shapes of the graphs of cardioids, limaçons, and lemniscates.
5) What part of the equation determines the shape of the graph of a polar equation?
- Answer
-
The shape of the polar graph is determined by whether or not it includes a sine, a cosine, and constants in the equation.
Graphical
For the exercises 6-15, test the equation for symmetry.
6) \(r=5\cos 3\theta\)
7) \(r=3-3\cos \theta\)
- Answer
-
symmetric with respect to the polar axis
8) \(r=3+2\sin \theta\)
9) \(r=3\sin 2\theta\)
- Answer
-
symmetric with respect to the polar axis, symmetric with respect to the line \(\theta = \dfrac{\pi }{2}\)
,
10) \(r=4\)
11) \(r=2\theta \)
- Answer
-
no symmetry
12) \(r=4\cos \dfrac{\theta }{2}\)
13) \(r=\dfrac{2}{\theta }\)
- Answer
-
no symmetry
14) \(r=3\sqrt{1-\cos ^2\theta }\)
15) \(r=\sqrt{5\sin 2\theta }\)
- Answer
-
symmetric with respect to the pole
For the exercises 16-43, graph the polar equation. Identify the name of the shape.
16) \(r=3\cos \theta\)
17) \(r=4\sin \theta\)
- Answer
-
circle
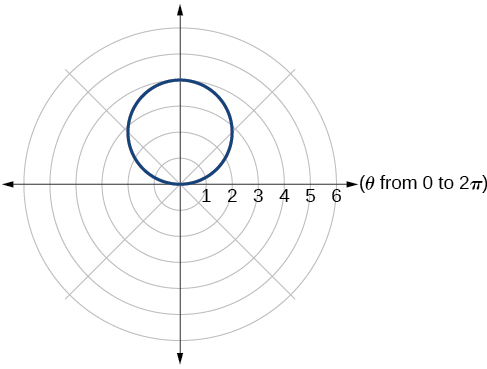
18) \(r=2+2\cos \theta\)
19) \(r=2-2\cos \theta\)
- Answer
-
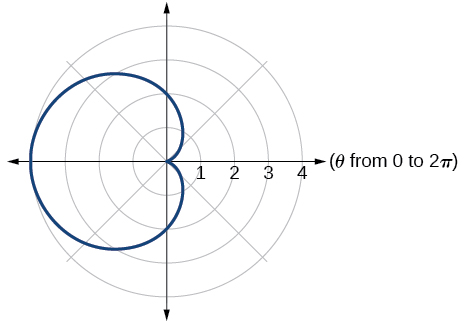
cardioid
20) \(r=5-5\sin \theta\)
21) \(r=3+3\sin \theta\)
- Answer
-
cardioid
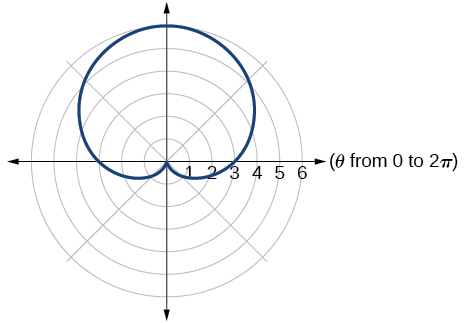
22) \(r=3+2\sin \theta\)
23) \(r=7+4\sin \theta\)
- Answer
-
one-loop/dimpled limaçon
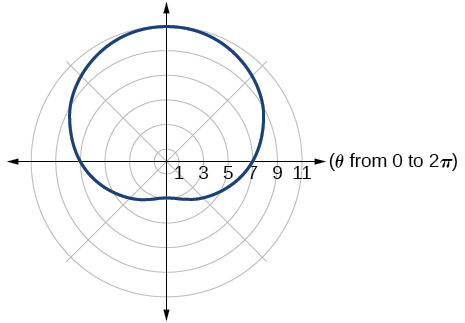
24) \(r=4+3\cos \theta\)
25) \(r=5+4cos \theta\)
- Answer
-
one-loop/dimpled limaçon
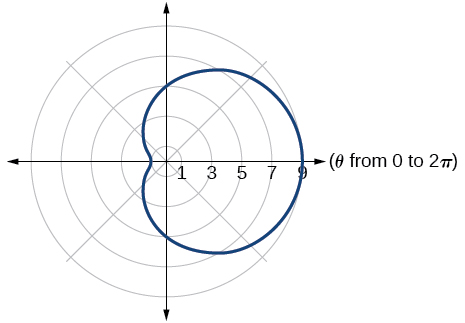
26) \(r=10+9\cos \theta\)
27) \(r=1+3\sin \theta\)
- Answer
-
inner loop/ two-loop limaçon
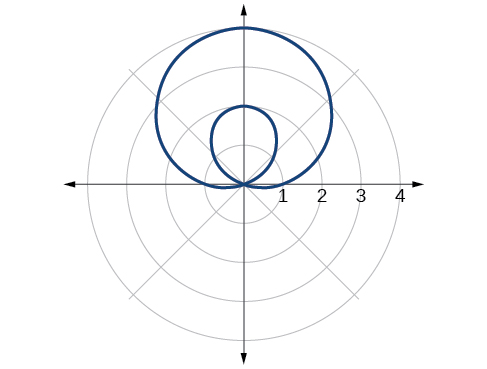
28) \(r=2+5\sin \theta\)
29) \(r=5+7\sin \theta\)
- Answer
-
inner loop/ two-loop limaçon
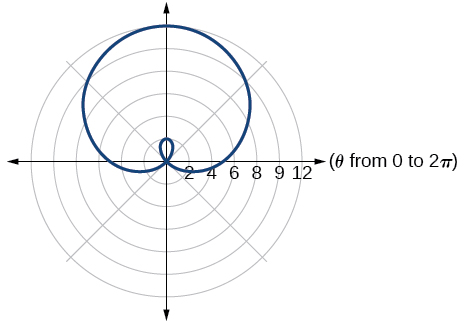
30) \(r=2+4\cos \theta\)
31) \(r=5+6\cos \theta\)
- Answer
-
inner loop/ two-loop limaçon
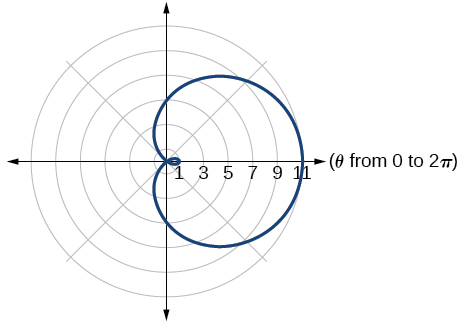
32) \(r^2=36\cos (2\theta )\)
33) \(r^2=10\cos (2\theta )\)
- Answer
-
lemniscate
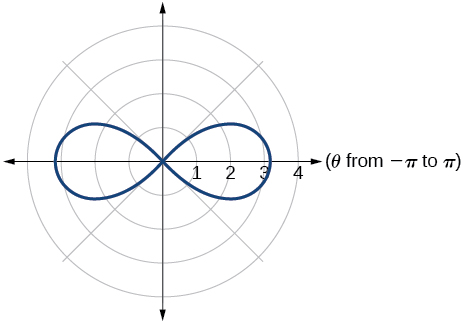
34) \(r^2=4\sin (2\theta )\)
35) \(r^2=10\sin (2\theta )\)
- Answer
-
lemniscate
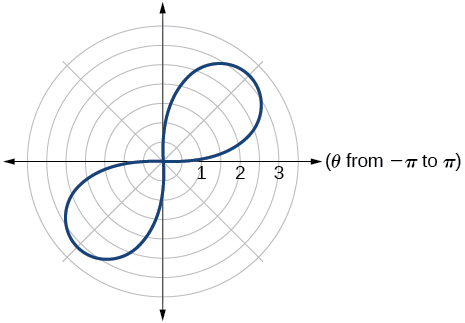
36) \(r=3\sin (2\theta )\)
37) \(r=3\cos (2\theta )\)
- Answer
-
rose curve
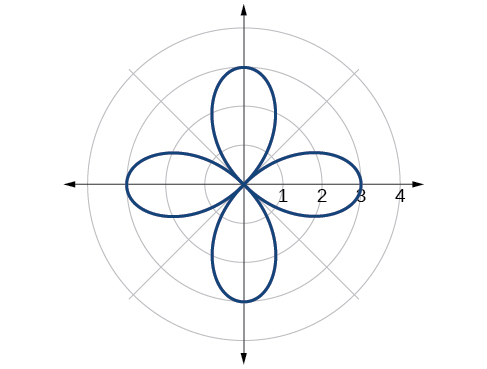
38) \(r=5\sin (3\theta )\)
39) \(r=4\sin (4\theta )\)
- Answer
-
rose curve
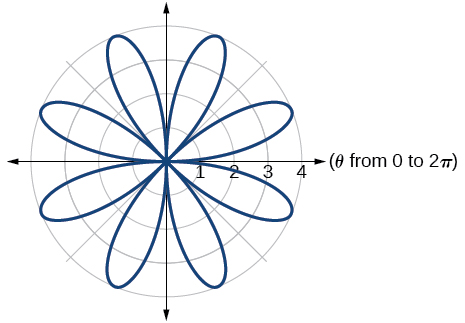
40) \(r=4\sin (5\theta )\)
41) \(r=-\theta\)
- Answer
-
Archimedes’ spiral
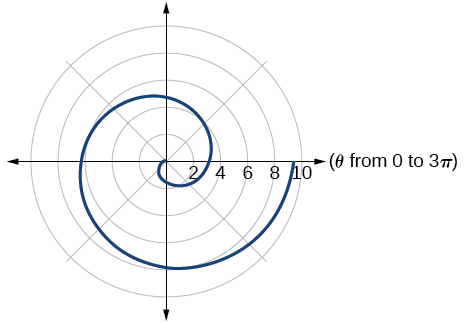
42) \(r=2\theta\)
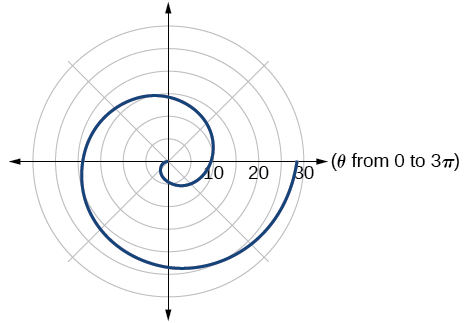
43) \(r=-3\theta\)
- Answer
-
Archimedes’ spiral
Technology
For the exercises 44-53, use a graphing calculator to sketch the graph of the polar equation.
44) \(r=\dfrac{1}{\theta }\)
45) \(r=\dfrac{1}{\sqrt{\theta }}\)
- Answer
-
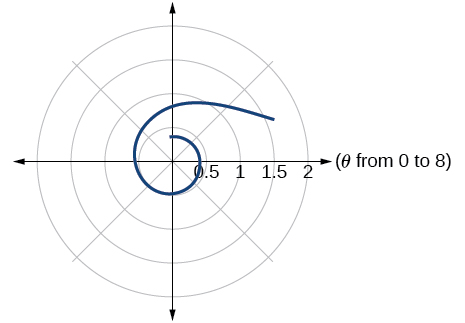
46) \(r=2\sin \theta \tan \theta\), a cissoid
47) \(r=2\sqrt{1-\sin ^2\theta }\), a hippopede
- Answer
-
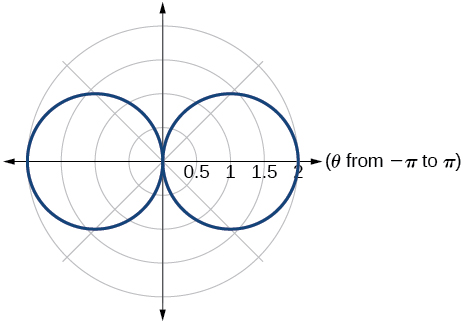
48) \(r=5+\cos (4\theta )\)
49) \(r=2-\sin (2\theta )\)
- Answer
-
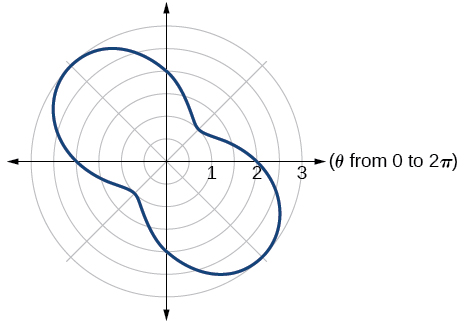
50) \(r=\theta ^2\)
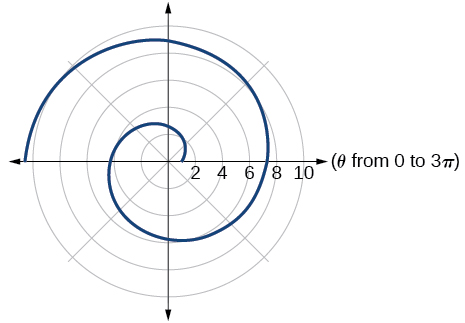
51) \(r=\theta +1\)
- Answer
-
52) \(r=\theta \sin \theta\)
53) \(r=\theta \cos \theta\)
- Answer
-
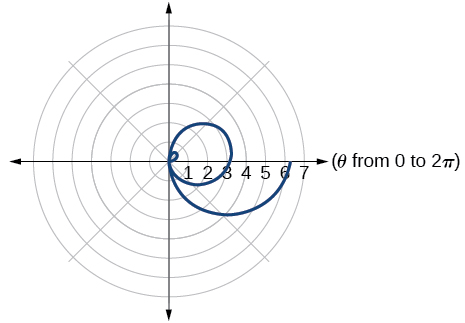
For the exercises 54-63, use a graphing utility to graph each pair of polar equations on a domain of \([0,4\pi ]\)and then explain the differences shown in the graphs.
54) \(r=\theta ,r=-\theta\)
55) \(r=\theta ,r=\theta +\sin \theta\)
- Answer
-
They are both spirals, but not quite the same.
56) \(r=\sin \theta +\theta ,r=\sin \theta -\theta\)
57) \(r=2\sin \left (\dfrac{\theta }{2} \right ),r=\theta \sin \left (\dfrac{\theta }{2} \right )\)
- Answer
-
Both graphs are curves with \(2\) loops. The equation with a coefficient of \(\theta \) has two loops on the left, the equation with a coefficient of \(2\) has two loops side by side. Graph these from \(0\) to \(4\pi \) to get a better picture.
58) \(r=\sin (\cos (3\theta )),r=\sin (3\theta )\)
59) On a graphing utility, graph \(r=\sin \left (\dfrac{16}{5}\theta \right )\) on \([0,4\pi ]\), \([0,8\pi ]\), \([0,12\pi ]\) and \([0,16\pi ]\)
- Answer
-
When the width of the domain is increased, more petals of the flower are visible.
60) On a graphing utility, graph and sketch \(r=\sin \theta + \left(\sin \left(\dfrac{5}{2}\theta \right) \right)^3\) on \([0,4\pi ]\).
61) On a graphing utility, graph each polar equation. Explain the similarities and differences you observe in the graphs. \[\begin{align*} r_1 &= 3\sin(3\theta )\\ r_2 &= 2\sin(3\theta )\\ r_3 &= \sin(3\theta ) \end{align*}\]
- Answer
-
The graphs are three-petal, rose curves. The larger the coefficient, the greater the curve’s distance from the pole.
62) On a graphing utility, graph each polar equation. Explain the similarities and differences you observe in the graphs. \[\begin{align*} r_1 &= 3+3\cos(\theta )\\ r_2 &= 2+2\cos(\theta )\\ r_3 &= 1+\cos(\theta ) \end{align*}\]
63) On a graphing utility, graph each polar equation. Explain the similarities and differences you observe in the graphs. \[\begin{align*} r_1 &= 3\theta \\ r_2 &= 2\theta \\ r_3 &= \theta \end{align*}\]
- Answer
-
The graphs are spirals. The smaller the coefficient, the tighter the spiral.
Extensions
For the exercises 64-72, draw each polar equation on the same set of polar axes, and find the points of intersection.
64) \(r_1=3+2\sin \theta , r_2=2\)
65) \(r_1=6-4\cos \theta , r_2=4\)
- Answer
-
\(\left ( 4,\dfrac{\pi }{3} \right ), \left ( 4,\dfrac{5\pi }{3} \right )\)
66) \(r_1=1+\sin \theta , r_2=3\sin \theta\)
67) \(r_1=1+\cos \theta , r_2=3\cos \theta\)
- Answer
-
\(\left ( \dfrac{3}{2},\dfrac{\pi }{3} \right ), \left ( \dfrac{3}{2},\dfrac{5\pi }{3} \right )\)
68) \(r_1=\cos (2\theta ), r_2=\sin (2\theta )\)
69) \(r_1=\sin ^2(2\theta ), r_2=1-\cos (4\theta )\)
- Answer
-
\(\left ( 0,\dfrac{\pi }{2} \right ), (0,\pi ), \left ( 0,\dfrac{3\pi }{2} \right ), (0,2\pi )\)
70) \(r_1=\sqrt{3}, r_2=2\sin (\theta )\)
71) \(r_1^2=\sin \theta , r_2^2=\cos \theta\)
- Answer
-
\(\left ( \dfrac{\sqrt[4]{8}}{2},\dfrac{\pi }{4} \right )\), \(\left ( \dfrac{\sqrt[4]{8}}{2},\dfrac{5\pi }{4} \right )\), and at \(\theta =\dfrac{3\pi }{4}\), \(\dfrac{7\pi }{4}\) since \(r\) is squared
72) \(r_1=1+\cos \theta , r_2=1-\sin \theta\)
8.5: Polar Form of Complex Numbers
Verbal
1) A complex number is \(a+bi\). Explain each part.
- Answer
-
\(a\) is the real part, \(b\) is the imaginary part, and \(i=\sqrt{-1}\)
2) What does the absolute value of a complex number represent?
3) How is a complex number converted to polar form?
- Answer
-
Polar form converts the real and imaginary part of the complex number in polar form using \(x=r\cos \theta\) and \(y=r\sin \theta\).
4) How do we find the product of two complex numbers?
5) What is De Moivre’s Theorem and what is it used for?
- Answer
-
\(z^n=r^n(\cos (n\theta )+i\sin (n\theta ))\)
It is used to simplify polar form when a number has been raised to a power.
Algebraic
For the exercises 6-11, find the absolute value of the given complex number.
6) \(5+3i\)
7) \(-7+i\)
- Answer
-
\(5\sqrt{2}\)
8) \(-3-3i\)
9) \(\sqrt{2}-6i\)
- Answer
-
\(\sqrt{38}\)
10) \(2i\)
11) \(2.2-3.1i\)
- Answer
-
\(\sqrt{14.45}\)
For the exercises 12-16, write the complex number in polar form.
12) \(2+2i\)
13) \(8-4i\)
- Answer
-
\(4\sqrt{5}\mathbf{cis}(333.4^{\circ})\)
14) \(-\dfrac{1}{2}-\dfrac{1}{2}i\)
15) \(\sqrt{3}+i\)
- Answer
-
\(2\mathbf{cis}\left ( \dfrac{\pi }{6} \right )\)
16) \(3i\)
For the exercises 17-22, convert the complex number from polar to rectangular form.
17) \(z=7\mathbf{cis}\left ( \dfrac{\pi }{6} \right )\)
- Answer
-
\(\dfrac{7\sqrt{3}}{2}+i\dfrac{7}{2}\)
18) \(z=2\mathbf{cis}\left ( \dfrac{\pi }{3} \right )\)
19) \(z=4\mathbf{cis}\left ( \dfrac{7\pi }{6} \right )\)
- Answer
-
\(-2\sqrt{3}-2i\)
20) \(z=7\mathbf{cis}(25^{\circ})\)
21) \(z=3\mathbf{cis}(240^{\circ})\)
- Answer
-
\(-1.5-i\dfrac{3\sqrt{3}}{2}\)
22) \(z=\sqrt{2}\mathbf{cis}(100^{\circ})\)
For the exercises 23-28, find \(z_1 z_2\) in polar form.
23) \(z_1=2\sqrt{3}\mathbf{cis}(116^{\circ}); z_2=2\mathbf{cis}(82^{\circ})\)
- Answer
-
\(4\sqrt{3}\mathbf{cis}(198^{\circ})\)
24) \(z_1=\sqrt{2}\mathbf{cis}(205^{\circ}); z_2=2\sqrt{2}\mathbf{cis}(118^{\circ})\)
25) \(z_1=3\mathbf{cis}(120^{\circ}); z_2=\dfrac{1}{4}\mathbf{cis}(60^{\circ})\)
- Answer
-
\(\dfrac{3}{4}\mathbf{cis}(180^{\circ})\)
26) \(z_1=3\mathbf{cis} \left(\dfrac{\pi }{4} \right); z_2=5\mathbf{cis}\left(\dfrac{\pi }{6} \right)\)
27) \(z_1=\sqrt{5}\mathbf{cis} \left(\dfrac{5\pi }{8} \right); z_2=\sqrt{15}\mathbf{cis}\left(\dfrac{\pi }{12} \right)\)
- Answer
-
\(5\sqrt{3}\mathbf{cis} \left(\dfrac{17\pi }{24} \right)\)
28) \(z_1=4\mathbf{cis} \left(\dfrac{\pi }{2} \right); z_2=2\mathbf{cis}\left(\dfrac{\pi }{4} \right)\)
For the exercises 29-,34 find \(\dfrac{z_1}{z_2}\) in polar form.
29) \(z_1=21\mathbf{cis}(135^{\circ}); z_2=3\mathbf{cis}(65^{\circ})\)
- Answer
-
\(7\mathbf{cis}(70^{\circ})\)
30) \(z_1=\sqrt{2}\mathbf{cis}(90^{\circ}); z_2=2\mathbf{cis}(60^{\circ})\)
31) \(z_1=15\mathbf{cis}(120^{\circ}); z_2=3\mathbf{cis}(40^{\circ})\)
- Answer
-
\(5\mathbf{cis}(80^{\circ})\)
32) \(z_1=6\mathbf{cis} \left(\dfrac{\pi }{3} \right); z_2=2\mathbf{cis}\left(\dfrac{\pi }{4} \right)\)
33) \(z_1=5\sqrt{2}\mathbf{cis} (\pi ); z_2=\sqrt{2}\mathbf{cis}\left(\dfrac{2\pi }{3} \right)\)
- Answer
-
\(5\mathbf{cis} \left(\dfrac{\pi }{3} \right)\)
34) \(z_1=2\mathbf{cis} \left(\dfrac{3\pi }{5} \right); z_2=3\mathbf{cis}\left(\dfrac{\pi }{4} \right)\)
For the exercises 35-40, find the powers of each complex number in polar form.
35) Find \(z^3\) when \(z=5\mathbf{cis} (45^{\circ})\).
- Answer
-
\(125\mathbf{cis} (135^{\circ})\)
36) Find \(z^4\) when \(z=2\mathbf{cis} (70^{\circ})\).
37) Find \(z^2\) when \(z=3\mathbf{cis} (120^{\circ})\).
- Answer
-
\(9\mathbf{cis} (240^{\circ})\)
38) Find \(z^2\) when \(z=4\mathbf{cis}\left(\dfrac{\pi }{4} \right)\).
39) Find \(z^4\) when \(z=\mathbf{cis}\left(\dfrac{3\pi }{16} \right)\).
- Answer
-
\(\mathbf{cis}\left(\dfrac{3\pi }{4} \right) \)
40) Find \(z^3\) when \(z=3\mathbf{cis}\left(\dfrac{5\pi }{3} \right)\).
For the exercises 41-45, evaluate each root.
41) Evaluate the cube root of \(z\) when \(z=27\mathbf{cis} (240^{\circ})\).
- Answer
-
\(3\mathbf{cis}(80^{\circ}), 3\mathbf{cis}(200^{\circ}), 3\mathbf{cis}(320^{\circ})\)
42) Evaluate the square root of \(z\) when \(z=16\mathbf{cis} (100^{\circ})\).
43) Evaluate the cube root of \(z\) when \(z=32\mathbf{cis} \left(\dfrac{2\pi }{3} \right)\).
- Answer
-
\(2\sqrt[3]{4}\mathbf{cis} \left(\dfrac{2\pi }{9} \right), 2\sqrt[3]{4}\mathbf{cis} \left(\dfrac{8\pi }{9} \right), 2\sqrt[3]{4}\mathbf{cis} \left(\dfrac{14\pi }{9} \right)\)
44) Evaluate the square root of \(z\) when \(z=32\mathbf{cis} (\pi )\).
45) Evaluate the cube root of \(z\) when \(z=8\mathbf{cis} \left(\dfrac{7\pi }{4} \right)\).
- Answer
-
\(2\sqrt{2}\mathbf{cis} \left(\dfrac{7\pi }{8} \right), 2\sqrt{2}\mathbf{cis} \left(\dfrac{15\pi }{8} \right)\)
Graphical
For the exercises 46-55, plot the complex number in the complex plane.
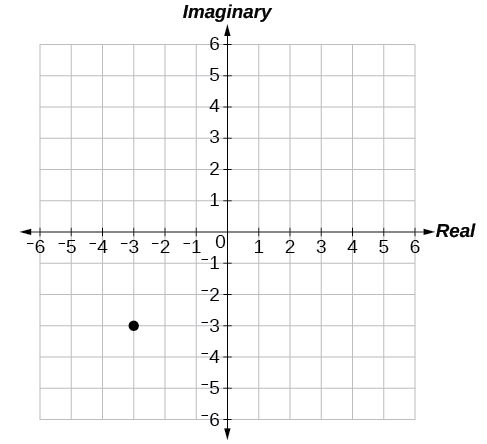
46) \(2+4i\)
47) \(-3-3i\)
- Answer
-
48) \(5-4i\)
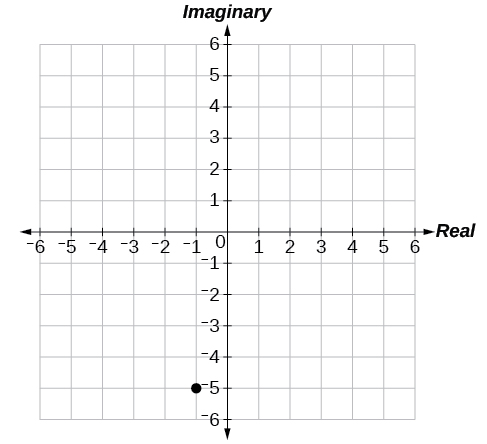
49) \(-1-5i\)
- Answer
-
50) \(3+2i\)
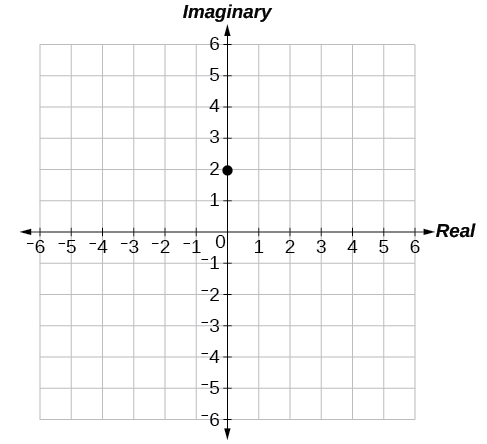
51) \(2i\)
- Answer
-
52) \(-4\)
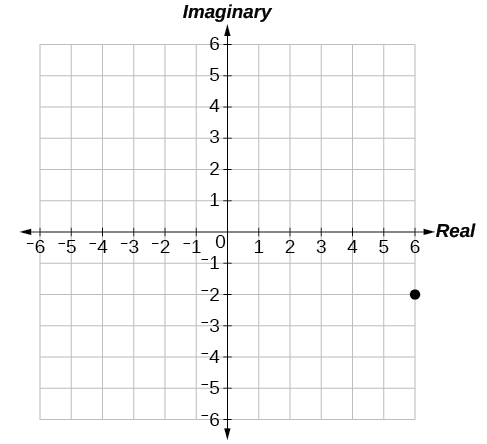
53) \(6-2i\)
- Answer
-
54) \(-2+i\)
55) \(1-4i\)
- Answer
-
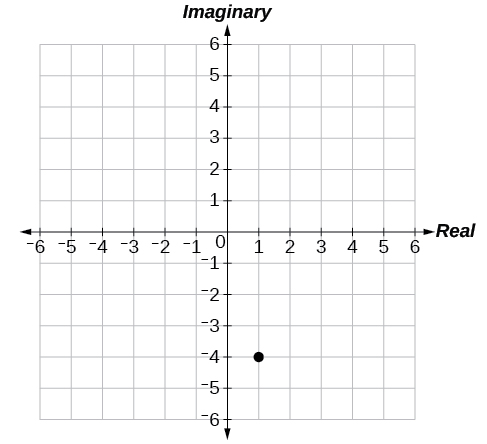
Technology
For the exercises 56-, find all answers rounded to the nearest hundredth.
56) Use the rectangular to polar feature on the graphing calculator to change \(5+5i\) to polar form.
57) Use the rectangular to polar feature on the graphing calculator to change \(3-2i\) to polar form.
- Answer
-
\(3.61e^{-0.59i}\)
58) Use the rectangular to polar feature on the graphing calculator to change \(-3-8i\) to polar form.
59) Use the polar to rectangular feature on the graphing calculator to change \(4\mathbf{cis} (120^{\circ})\) to rectangular form.
- Answer
-
\(-2+3.46i\)
60) Use the polar to rectangular feature on the graphing calculator to change \(2\mathbf{cis} (45^{\circ})\) to rectangular form.
61) Use the polar to rectangular feature on the graphing calculator to change \(5\mathbf{cis} (210^{\circ})\) to rectangular form.
- Answer
-
\(-4.33-2.50i\)
8.6: Parametric Equations
Verbal
1) What is a system of parametric equations?
- Answer
-
A pair of functions that is dependent on an external factor. The two functions are written in terms of the same parameter. For example, \(x=f(t)\) and \(y=f(t)\).
2) Some examples of a third parameter are time, length, speed, and scale. Explain when time is used as a parameter.
3) Explain how to eliminate a parameter given a set of parametric equations.
- Answer
-
Choose one equation to solve for \(t\), substitute into the other equation and simplify.
4) What is a benefit of writing a system of parametric equations as a Cartesian equation?
5) What is a benefit of using parametric equations?
- Answer
-
Some equations cannot be written as functions, like a circle. However, when written as two parametric equations, separately the equations are functions.
6) Why are there many sets of parametric equations to represent on Cartesian function?
Algebraic
For the exercises 7-25, eliminate the parameter \(t\) to rewrite the parametric equation as a Cartesian equation.
7) \(\begin{cases} & x(t)= 5-t\\ & y(t)= 8-2t \end{cases}\)
- Answer
-
\(y=-2+2x\)
8) \(\begin{cases} & x(t)= 6-3t\\ & y(t)= 10-t \end{cases}\)
9) \(\begin{cases} & x(t)= 2t+1\\ & y(t)= 3\sqrt{t} \end{cases}\)
- Answer
-
\(y=3\sqrt{\dfrac{x-1}{2}}\)
10) \(\begin{cases} & x(t)= 3t-1\\ & y(t)= 2t^2 \end{cases}\)
11) \(\begin{cases} & x(t)= 2e^t\\ & y(t)= 1-5t \end{cases}\)
- Answer
-
\(x=2e^{\tfrac{1-y}{5}}\) or \(y=1-5\ln \left ( \dfrac{x}{2} \right )\)
12) \(\begin{cases} & x(t)= e^{-2t}\\ & y(t)= 2e^{-t} \end{cases}\)
13) \(\begin{cases} & x(t)= 4\log (t)\\ & y(t)= 3+2t \end{cases}\)
- Answer
-
\(x=4\log \left ( \dfrac{y-3}{2} \right )\)
14) \(\begin{cases} & x(t)= \log (2t)\\ & y(t)= \sqrt{t-1} \end{cases}\)
15) \(\begin{cases} & x(t)= t^3-t\\ & y(t)= 2t \end{cases}\)
- Answer
-
\(x=\left ( \dfrac{y}{2} \right )^3-\dfrac{y}{2}\)
16) \(\begin{cases} & x(t)= t-t^4\\ & y(t)= t+2 \end{cases}\)
17) \(\begin{cases} & x(t)= e^{2t}\\ & y(t)= e^{6t} \end{cases}\)
- Answer
-
\(y=x^3\)
18) \(\begin{cases} & x(t)= t^{5}\\ & y(t)= t^{10} \end{cases}\)
19) \(\begin{cases} & x(t)= 4\cos t\\ & y(t)= 5\sin t \end{cases}\)
- Answer
-
\(\left ( \dfrac{x}{4} \right )^2+\left ( \dfrac{y}{5} \right )^2=1\)
20) \(\begin{cases} & x(t)= 3\sin t\\ & y(t)= 6\cos t \end{cases}\)
21) \(\begin{cases} & x(t)= 2\cos ^2t\\ & y(t)= -\sin t \end{cases}\)
- Answer
-
\(y^2=1-\dfrac{1}{2}x\)
22) \(\begin{cases} & x(t)= \cos t+4\\ & y(t)= 2\sin ^2t \end{cases}\)
23) \(\begin{cases} & x(t)= t-1\\ & y(t)= t^2 \end{cases}\)
- Answer
-
\(y=x^2+2x+1\)
24) \(\begin{cases} & x(t)= -t\\ & y(t)= t^3+1 \end{cases}\)
25) \(\begin{cases} & x(t)= 2t-1\\ & y(t)= t^3-2 \end{cases}\)
- Answer
-
\(y=\left ( \dfrac{x+1}{2} \right )^3 - 2\)
For the exercises 26-29, rewrite the parametric equation as a Cartesian equation by building an \(x-y\) table.
26) \(\begin{cases} & x(t)= 2t-1\\ & y(t)= t+4 \end{cases}\)
27) \(\begin{cases} & x(t)= 4-t\\ & y(t)= 3t+2 \end{cases}\)
- Answer
-
\(y=-3x+14\)
28) \(\begin{cases} & x(t)= 2t-1\\ & y(t)= 5t \end{cases}\)
29) \(\begin{cases} & x(t)= 4t-1\\ & y(t)= 4t+2 \end{cases}\)
- Answer
-
\(y=x+3\)
For the exercises 30-33, parameterize (write parametric equations for) each Cartesian equation by setting \(x(t)=t\) or by setting \(y(t)=t\).
30) \(y(x)=3x^2 + 3\)
31) \(y(x)=2\sin x + 1\)
- Answer
-
\(\begin{cases} & x(t)= t\\ & y(t)= 2\sin t + 1 \end{cases}\)
32) \(x(y)=3\log (y)+y\)
33) \(x(y)=\sqrt{y}+2y\)
- Answer
-
\(\begin{cases} & x(t)= \sqrt{t}+2t\\ & y(t)= t \end{cases}\)
For the exercises 34-41, parameterize (write parametric equations for) each Cartesian equation by using \(x(t)=a\cos t\) and \(y(t)=b\sin t\). Identify the curve.
34) \(\dfrac{x^2}{4}+\dfrac{x^2}{9}=1\)
35) \(\dfrac{x^2}{16}+\dfrac{x^2}{36}=1\)
- Answer
-
\(\begin{cases} & x(t)= 4\cos t\\ & y(t)= 6\sin t \end{cases}; \text{Ellipse}\)
36) \(x^2 + y^2 = 16\)
37) \(x^2 + y^2 = 10\)
- Answer
-
\(\begin{cases} & x(t)= \sqrt{10}\cos t\\ & y(t)= \sqrt{10}\sin t \end{cases}; \text{Circle}\)
38) Parameterize the line from \((3,0)\) to \((-2,-5)\) so that the line is at \((3,0)\) at \(t=0\), and at \((-2,-5)\) at \(t=1\).
39) Parameterize the line from \((-1,0)\) to \((3,-2)\) so that the line is at \((-1,0)\) at \(t=0\), and at \((3,-2)\) at \(t=1\).
- Answer
-
\(\begin{cases} & x(t)= -1+4t\\ & y(t)= -2t \end{cases}\)
40) Parameterize the line from \((-1,5)\) to \((2,3)\) so that the line is at \((-1,5)\) at \(t=0\), and at \((2,3)\) at \(t=1\).
41) Parameterize the line from \((4,1)\) to \((6,-2)\) so that the line is at \((4,1)\) at \(t=0\), and at \((6,-2)\) at \(t=1\).
- Answer
-
\(\begin{cases} & x(t)= 4+2t\\ & y(t)= 1-3t \end{cases}\)
Technology
For the exercises 42-43, use the table feature in the graphing calculator to determine whether the graphs intersect.
42) \(\begin{cases} & x_1(t)= 3t\\ & y_1(t)= 2t-1 \end{cases}\; \; \text{and}\; \; \begin{cases} & x_2(t)= t+3\\ & y_2(t)= 4t-4 \end{cases}\)
43) \(\begin{cases} & x_1(t)= t^2\\ & y_1(t)= 2t-1 \end{cases}\; \; \text{and}\; \; \begin{cases} & x_2(t)= -t+6\\ & y_2(t)= t+1 \end{cases}\)
- Answer
-
yes, at \(t=2\)
For the exercises 44-46, use a graphing calculator to complete the table of values for each set of parametric equations.
44) \(\begin{cases} & x_1(t)= 3t^2-3t+7\\ & y_1(t)= 2t+3 \end{cases}\)
| \(t\) | \(x\) | \(y\) |
|---|---|---|
| -1 | ||
| 0 | ||
| 1 |
45) \(\begin{cases} & x_1(t)= t^2-4\\ & y_1(t)= 2t^2-1 \end{cases}\)
| \(t\) | \(x\) | \(y\) |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 |
- Answer
-
\(t\) \(x\) \(y\) 1 -3 1 2 0 7 3 5 17
46) \(\begin{cases} & x_1(t)= t^4\\ & y_1(t)= t^3+4 \end{cases}\)
| \(t\) | \(x\) | \(y\) |
|---|---|---|
| -1 | ||
| 0 | ||
| 1 | ||
| 2 |
Extensions
47) Find two different sets of parametric equations for \(y=(x+1)^2\).
- Answer
-
answers may vary: \(\begin{cases} & x(t)= t-1\\ & y(t)= t^2 \end{cases}\; \; \text{and}\; \; \begin{cases} & x(t)= t+1\\ & y(t)= (t+2)^2 \end{cases}\)
48) Find two different sets of parametric equations for \(y=3x-2\).
49) Find two different sets of parametric equations for \(y=x^2-4x+4\).
- Answer
-
answers may vary: \(\begin{cases} & x(t)= t\\ & y(t)= t^2-4t+4 \end{cases}\; \; \text{and}\; \; \begin{cases} & x(t)= t+2\\ & y(t)= t^2 \end{cases}\)
8.7: Parametric Equations - Graphs
Verbal
1) What are two methods used to graph parametric equations?
- Answer
-
plotting points with the orientation arrow and a graphing calculator
2) What is one difference in point-plotting parametric equations compared to Cartesian equations?
3) Why are some graphs drawn with arrows?
- Answer
-
The arrows show the orientation, the direction of motion according to increasing values of \(t\).
4) Name a few common types of graphs of parametric equations.
5) Why are parametric graphs important in understanding projectile motion?
- Answer
-
The parametric equations show the different vertical and horizontal motions over time.
Graphical
For the exercises 6-11, graph each set of parametric equations by making a table of values. Include the orientation on the graph.
6) \(\begin{cases} & x(t)= t\\ & y(t)= t^2-1 \end{cases}\)
| \(t\) | \(x\) | \(y\) |
|---|---|---|
| -3 | ||
| -2 | ||
| -1 | ||
| 0 | ||
| 1 | ||
| 2 | ||
| 3 |
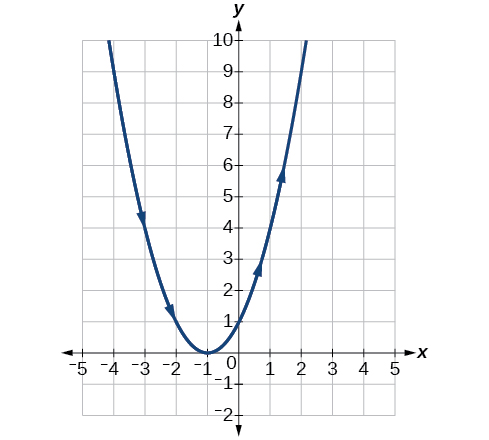
7) \(\begin{cases} & x(t)= t-1\\ & y(t)= t^2 \end{cases}\)
| \(t\) | -3 | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|---|
| \(x\) | ||||||
| \(y\) |
- Answer
-
8) \(\begin{cases} & x(t)= 2+t\\ & y(t)= 3-2t \end{cases}\)
| \(t\) | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|
| \(x\) | ||||||
| \(y\) |
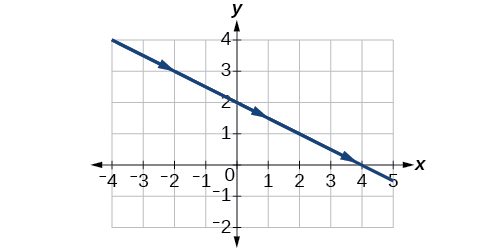
9) \(\begin{cases} & x(t)= -2-2t\\ & y(t)= 3+t \end{cases}\)
| \(t\) | -3 | -2 | -1 | 0 | 1 |
|---|---|---|---|---|---|
| \(x\) | |||||
| \(y\) |
- Answer
-
10) \(\begin{cases} & x(t)= t^3\\ & y(t)= t+2 \end{cases}\)
| \(t\) | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| \(x\) | |||||
| \(y\) |
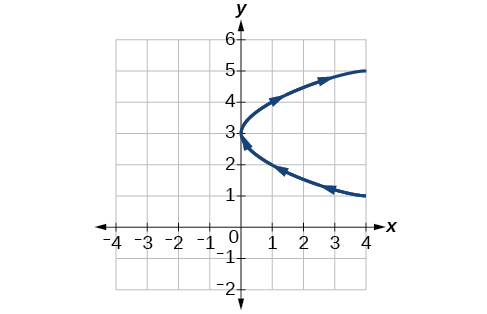
11) \(\begin{cases} & x(t)= t^2\\ & y(t)= t+3 \end{cases}\)
| \(t\) | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| \(x\) | |||||
| \(y\) |
- Answer
-
For the exercises 12-22, sketch the curve and include the orientation.
12) \(\begin{cases} & x(t)= t\\ & y(t)= \sqrt{t} \end{cases}\)
13) \(\begin{cases} & x(t)= -\sqrt{t}\\ & y(t)= t \end{cases}\)
- Answer
-
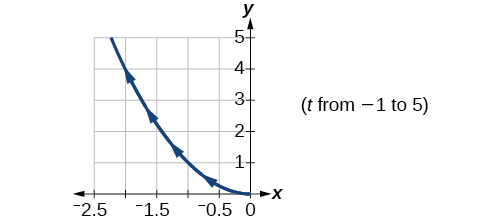
14) \(\begin{cases} & x(t)= 5-\left | t \right |\\ & y(t)= t+2 \end{cases}\)
15) \(\begin{cases} & x(t)= -t+2\\ & y(t)= 5-\left | t \right | \end{cases}\)
- Answer
-
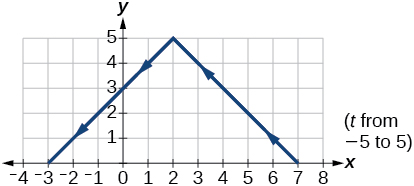
16) \(\begin{cases} & x(t)= 4\sin t\\ & y(t)= 2\cos t \end{cases}\)
17) \(\begin{cases} & x(t)= 2\sin t\\ & y(t)= 4\cos t \end{cases}\)
- Answer
-
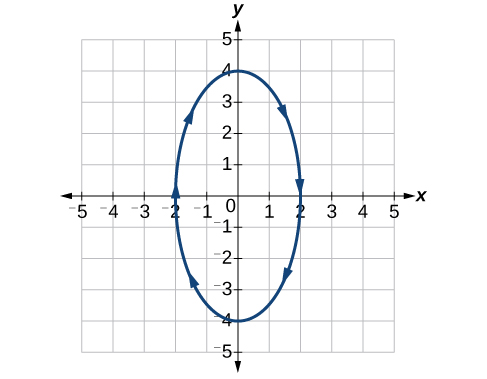
18) \(\begin{cases} & x(t)= 3\cos ^2t\\ & y(t)= -3\sin t \end{cases}\)
19) \(\begin{cases} & x(t)= 3\cos ^2t\\ & y(t)= -3\sin ^2t \end{cases}\)
- Answer
-
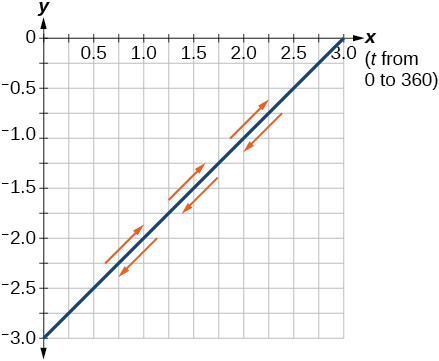
20) \(\begin{cases} & x(t)= \sec t\\ & y(t)= \tan t \end{cases}\)
21) \(\begin{cases} & x(t)= \sec t\\ & y(t)= \tan ^2t \end{cases}\)
- Answer
-
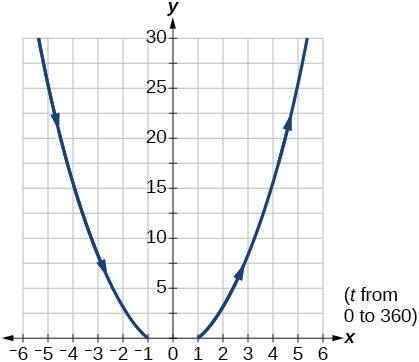
22) \(\begin{cases} & x(t)= \dfrac{1}{e^{2t}}\\ & y(t)= e^{-t} \end{cases}\)
For the exercises 23-27, graph the equation and include the orientation. Then, write the Cartesian equation.
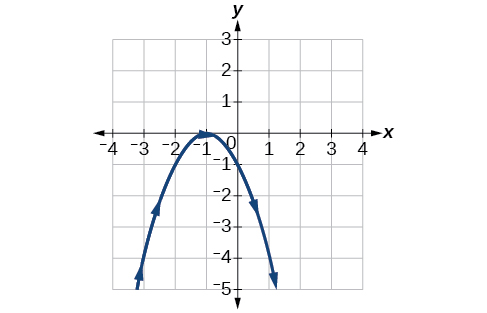
23) \(\begin{cases} & x(t)= t-1\\ & y(t)= -t^2 \end{cases}\)
- Answer
-
24) \(\begin{cases} & x(t)= t^3\\ & y(t)= t+3 \end{cases}\)
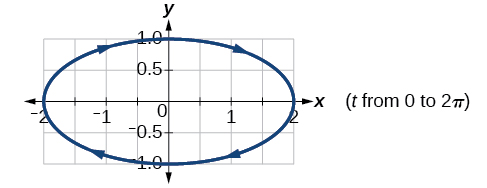
25) \(\begin{cases} & x(t)= 2\cos t\\ & y(t)= -\sin t \end{cases}\)
- Answer
-
26) \(\begin{cases} & x(t)= 7\cos t\\ & y(t)= 7\sin t \end{cases}\)
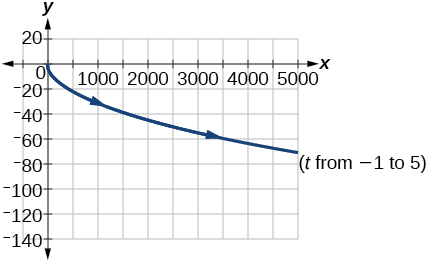
27) \(\begin{cases} & x(t)= e^{2t}\\ & y(t)= -e^{t} \end{cases}\)
- Answer
-
For the exercises 28-33, graph the equation and include the orientation.
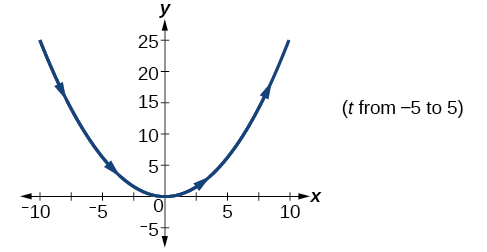
28) \(x=t^2, y = 3t, 0\leq t\leq 5\)
29) \(x=2t, y = t^2, -5\leq t\leq 5\)
- Answer
-
30) \(x=t, y=\sqrt{25-t^2}, 0<t\leq 5\)
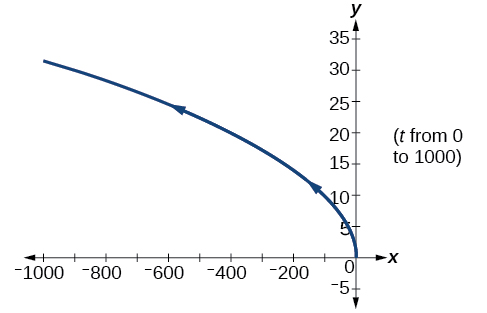
31) \(x(t)=-t,y(t)=\sqrt{t}, t\geq 0\)
- Answer
-
32) \(x=-2\cos t, y=6\sin t, 0\leq t\leq \pi\)
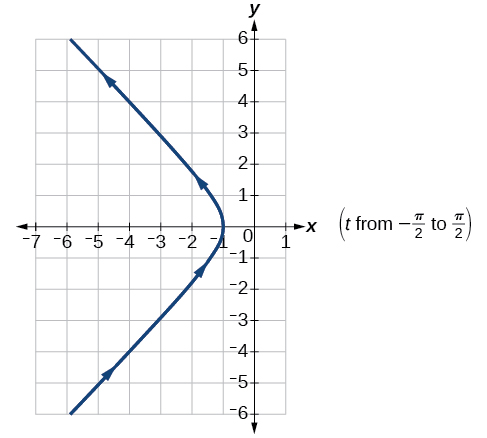
33) \(x=-\sec t, y=\tan t, -\dfrac{\pi }{2}< t< \dfrac{\pi }{2}\)
- Answer
-
For the exercises 34-41, use the parametric equations for integers \(a\) and \(b\): \[\begin{align*} x(t) &= a\cos ((a+b)t)\\ y(t) &= a\cos ((a-b)t) \end{align*} \nonumber\]
34) Graph on the domain \([-\pi ,0]\), where \(a=2\) and \(b=1\), and include the orientation.
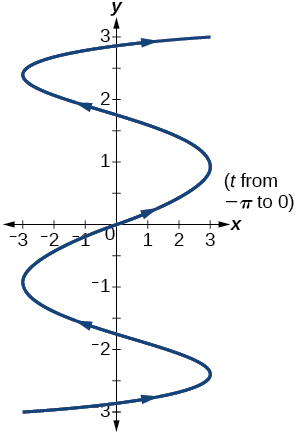
35) Graph on the domain \([-\pi ,0]\), where \(a=3\) and \(b=2\), and include the orientation.
- Answer
-
36) Graph on the domain \([-\pi ,0]\), where \(a=4\) and \(b=3\), and include the orientation.
37) Graph on the domain \([-\pi ,0]\), where \(a=5\) and \(b=4\), and include the orientation.
- Answer
-
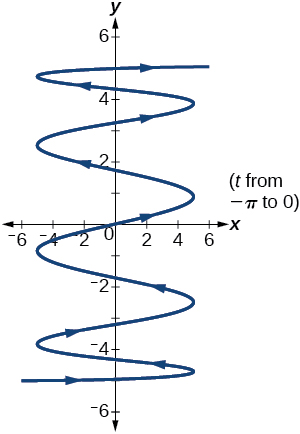
38) If \(a\) is \(1\) more than \(b\), describe the effect the values of \(a\) and \(b\) have on the graph of the parametric equations.
39) Describe the graph if \(a=100\) and \(b=99\).
- Answer
-
There will be \(100\) back-and-forth motions.
40) What happens if \(b\)
41) If the parametric equations \(x(t)=t^2\) and \(y(t)=6-3t\) have the graph of a horizontal parabola opening to the right, what would change the direction of the curve?
- Answer
-
Take the opposite of the \(x(t)\) equation.
For the exercises 42-46, describe the graph of the set of parametric equations.
42) \(x(t)=-t^2\) and \(y(t)\) is linear
43) \(y(t)=t^2\) and \(x(t)\) is linear
- Answer
-
The parabola opens up.
44) \(y(t)=-t^2\) and \(x(t)\) is linear
45) Write the parametric equations of a circle with center \((0,0)\)
- Answer
-
\(\begin{cases} & x(t)= 5\cos t\\ & y(t)= 5\sin t \end{cases}\)
46) Write the parametric equations of an ellipse with center \((0,0)\)
For the exercises 47-52, use a graphing utility to graph on the window \([-3,3]\) by \([-3,3]\) on the domain \([0,2\pi )\) for the following values of \(a\) and \(b\), and include the orientation. \[\begin{cases} & x(t)= \sin (at)\\ & y(t)= \sin (bt) \end{cases} \nonumber\]
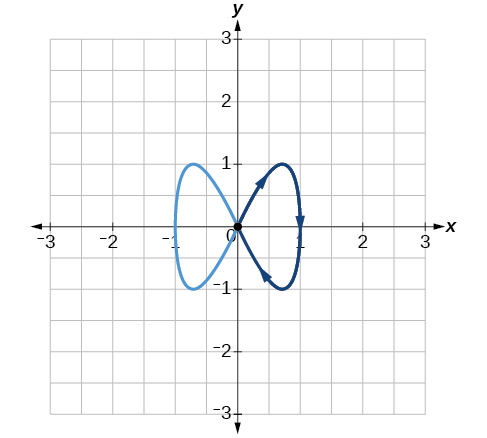
47) \(a=1,b=2\)
- Answer
-
48) \(a=2, b=1\)
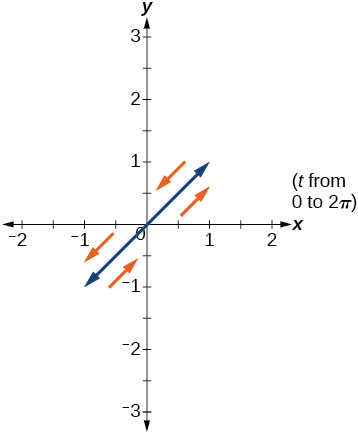
49) \(a=3, b=3\)
- Answer
-
50) \(a=5, b=5\)
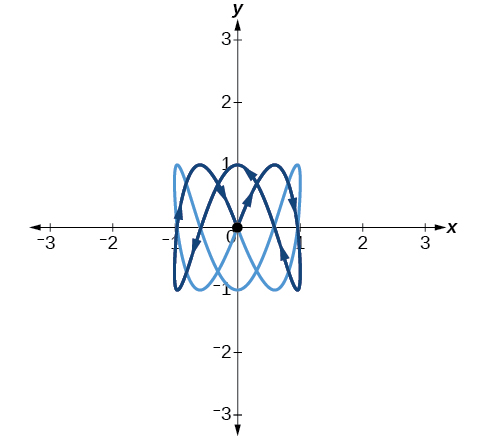
51) \(a=2, b=5\)
- Answer
-
52) \(a=5, b=2\)
Technology
For the exercises 53-56, look at the graphs that were created by parametric equations of the form \[\begin{cases} & x(t)= a\cos (bt)\\ & y(t)= c\sin (dt) \end{cases} \nonumber\]Use the parametric mode on the graphing calculator to find the values of \(a, b, c \), and \(d\) to achieve each graph.
53)
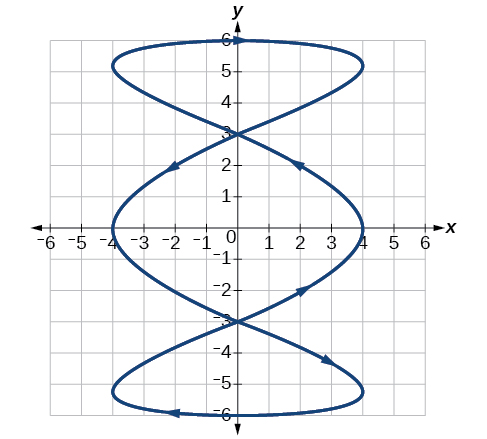
- Answer
-
\(a=4, b=3, c=6, d=1\)
54)
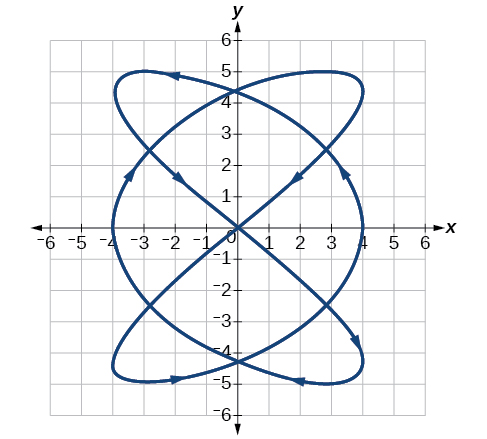
55)
- Answer
-
\(a=4, b=2, c=3, d=3\)
56)
For the exercises 57-62, use a graphing utility to graph the given parametric equations.
\[\begin{cases} & x(t)= \cos t-1\\ & y(t)= \sin t+t \end{cases} \nonumber\]
\[\begin{cases} & x(t)= \cos t+t\\ & y(t)= \sin t-1 \end{cases} \nonumber\]
\[\begin{cases} & x(t)= t-\sin t\\ & y(t)= \cos t-1 \end{cases} \nonumber\]
57) Graph all three sets of parametric equations on the domain \([0,2\pi ]\).
- Answer
-
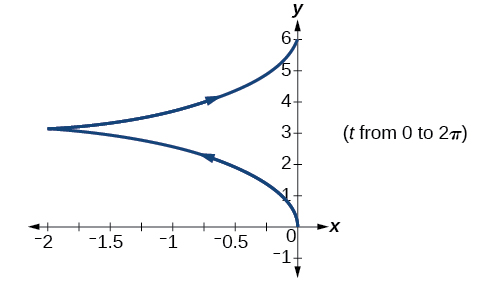
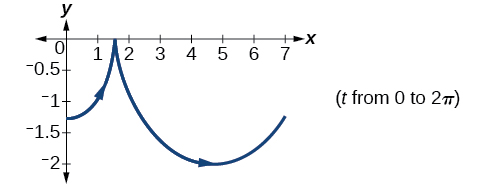
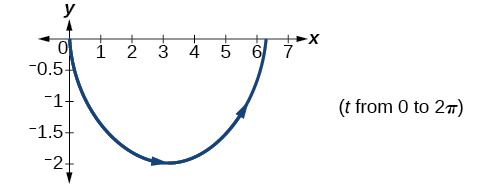
58) Graph all three sets of parametric equations on the domain \([0,4\pi]\).
59) Graph all three sets of parametric equations on the domain \([-4\pi ,6\pi]\).
- Answer
-
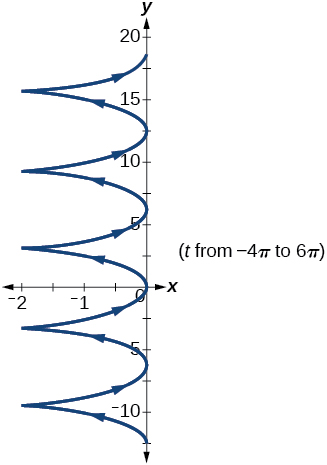
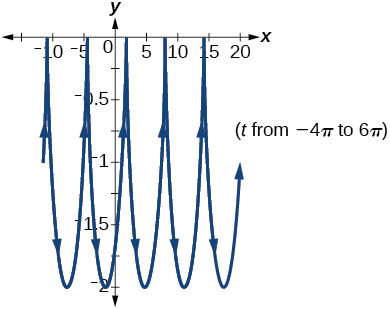
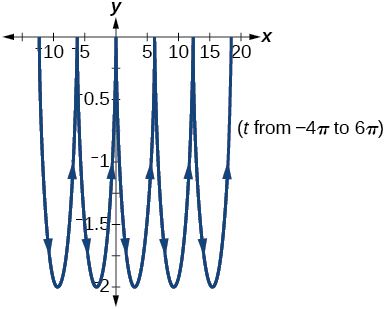
60) The graph of each set of parametric equations appears to “creep” along one of the axes. What controls which axis the graph creeps along?
61) Explain the effect on the graph of the parametric equation when we switched \(\sin t\) and \(\cos t\).
- Answer
-
The \(y\)-intercept changes.
62) Explain the effect on the graph of the parametric equation when we changed the domain.
Extensions
63) An object is thrown in the air with vertical velocity of \(20\) ft/s and horizontal velocity of \(15\) ft/s. The object’s height can be described by the equation \(y(t)=-16t^2+20t\), while the object moves horizontally with constant velocity \(15\) ft/s. Write parametric equations for the object’s position, and then eliminate time to write height as a function of horizontal position.
- Answer
-
\(y(x)=-16\left ( \dfrac{x}{15} \right )^2+20\left ( \dfrac{x}{15} \right )\)
64) A skateboarder riding on a level surface at a constant speed of \(9\) ft/s throws a ball in the air, the height of which can be described by the equation \(y(t)=-16t^2+10t+5\). Write parametric equations for the ball’s position, and then eliminate time to write height as a function of horizontal position.
For the exercises 65-69, use this scenario: A dart is thrown upward with an initial velocity of \(65\) ft/s at an angle of elevation of \(52^{\circ}\). Consider the position of the dart at any time \(t\). Neglect air resistance.
65) Find parametric equations that model the problem situation.
- Answer
-
\(\begin{cases} & x(t)= 64t\cos (52^{\circ})\\ & y(t)= -16t^2+64t\sin (52^{\circ}) \end{cases}\)
66) Find all possible values of \(x\) that represent the situation.
67) When will the dart hit the ground?
- Answer
-
approximately \(3.2\) seconds
68) Find the maximum height of the dart.
69) At what time will the dart reach maximum height?
- Answer
-
\(1.6\) seconds
For the exercises 70-73, look at the graphs of each of the four parametric equations. Although they look unusual and beautiful, they are so common that they have names, as indicated in each exercise. Use a graphing utility to graph each on the indicated domain.
70) \(\text{An epicycloid}\begin{cases} & x(t)= 14\cos t-\cos (14t)\\ & y(t)= 14\sin t+\sin (14t) \end{cases}\; \; \text{on the domain }[0,2\pi ]\)
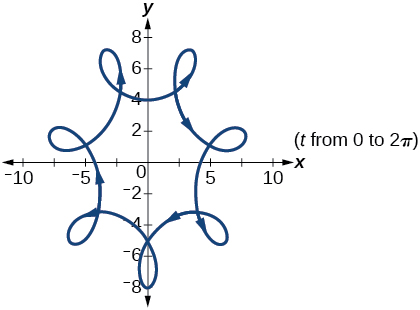
71) \(\text{An hypocycloid}\begin{cases} & x(t)= 6\sin t+2\sin (6t)\\ & y(t)= 6\cos t-2\cos (6t) \end{cases}\; \; \text{on the domain }[0,2\pi ]\)
- Answer
-
72) \(\text{An hypotrochoid}\begin{cases} & x(t)= 2\sin t+5\cos (6t)\\ & y(t)= 5\cos t-2\sin (6t) \end{cases}\; \; \text{on the domain }[0,2\pi ]\)
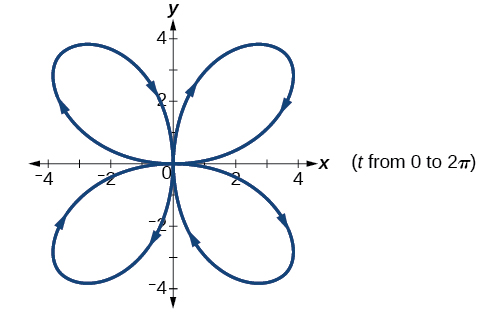
73) \(\text{A rose}\begin{cases} & x(t)= 5\sin (2t)\sin t\\ & y(t)= 5\sin (2t)\cos t \end{cases}\; \; \text{on the domain }[0,2\pi ]\)
- Answer
-
8.8: Vectors
Verbal
1) What are the characteristics of the letters that are commonly used to represent vectors?
- Answer
-
lowercase, bold letter, usually \(u, v, w\)
2) How is a vector more specific than a line segment?
3) What are \(i\) and \(j\), and what do they represent?
- Answer
-
They are unit vectors. They are used to represent the horizontal and vertical components of a vector. They each have a magnitude of \(1\).
4) What is component form?
5) When a unit vector is expressed as \(\left \langle a,b \right \rangle\) which letter is the coefficient of the \(i\) and which the \(j\)?
- Answer
-
The first number always represents the coefficient of the \(i\) and the second represents the \(j\).
Algebraic
6) Given a vector with initial point \((5,2)\) and terminal point \((-1,-3)\), find an equivalent vector whose initial point is \((0,0)\). Write the vector in component form \(\left \langle a,b \right \rangle\).
7) Given a vector with initial point \((-4,2)\) and terminal point \((3,-3)\), find an equivalent vector whose initial point is \((0,0)\). Write the vector in component form \(\left \langle a,b \right \rangle\).
- Answer
-
\(\left \langle 7,-5 \right \rangle\)
8) Given a vector with initial point \((7,-1)\) and terminal point \((-1,-7)\), find an equivalent vector whose initial point is \((0,0)\). Write the vector in component form \(\left \langle a,b \right \rangle\).
For the exercises 9-15, determine whether the two vectors \(u\) and \(v\) are equal, where \(u\) has an initial point \(P_1\) and a terminal point \(P_2\) and \(v\) has an initial point \(P_3\) and a terminal point \(P_4\).
9) \(P_1=(5,1), P_2=(3,-2), P_3=(-1,3), P4=(9,−4)\)
- Answer
-
not equal
10) \(P_1=(2,-3), P_2=(5,1), P_3=(6,-1), P_4=(9,3)\)
11) \(P_1=(-1,-1), P_2=(-4,5), P_3=(-10,6), P_4=(-13,12)\)
- Answer
-
equal
12) \(P_1=(3,7), P_2=(2,1), P_3=(1,2), P_4=(-1,-4)\)
13) \(P_1=(8,3), P_2=(6,5), P_3=(11,8), P4=(9,10)\)
- Answer
-
equal
14) Given initial point \(P_1=(-3,1)\) and terminal point \(P_2=(5,2)\), write the vector \(v\) in terms of \(i\) and \(j\).
15) Given initial point \(P_1=(6,0)\) and terminal point \(P_2=(-1,-3)\), write the vector \(v\) in terms of \(i\) and \(j\).
- Answer
-
\(7i-3j\)
For the exercises 16-17, use the vectors \(u = i+5j, v = -2i-3j, w = 4i-j\)
16) Find \(u+(v-w)\)
17) Find \(4v+2u\)
- Answer
-
\(-6i-2j\)
For the exercises 18-21, use the given vectors to compute \(u + v, u - v, 2u - 3v\)
18) \(u=\left \langle 2,-3 \right \rangle, v=\left \langle 1,5 \right \rangle\)
19) \(u=\left \langle -3,4 \right \rangle, v=\left \langle -2,1 \right \rangle\)
- Answer
-
\(u+v=\left \langle -5,5 \right \rangle,u-v=\left \langle -1,3 \right \rangle,2u-3v=\left \langle 0,5 \right \rangle\)
20) Let \(v = -4i + 3j\). Find a vector that is half the length and points in the same direction as \(v\).
21) Let \(v = 5i + 2j\). Find a vector that is twice the length and points in the opposite direction as \(v\).
- Answer
-
\(-10i-4j\)
For the exercises 22-27, find a unit vector in the same direction as the given vector.
22) \(a = 3i + 4j\)
23) \(b = -2i + 5j\)
- Answer
-
\(-\dfrac{2\sqrt{29}}{29}i+\dfrac{5\sqrt{29}}{29}j\)
24) \(c = 10i - j\)
25) \(d=-\dfrac{1}{3}i+\dfrac{5}{2}j\)
- Answer
-
\(-\dfrac{2\sqrt{229}}{229}i+\dfrac{15\sqrt{229}}{229}j\)
26) \(u = 100i + 200j\)
27) \(u = -14i + 2j\)
- Answer
-
\(-\dfrac{7\sqrt{2}}{10}i+\dfrac{\sqrt{2}}{10}j\)
For the exercises 28-35, find the magnitude and direction of the vector, \(0\leq \theta < 2\pi\).
28) \(\left \langle 0,4 \right \rangle\)
29) \(\left \langle 6,5 \right \rangle\)
- Answer
-
\(\left | v \right |=7.810, \theta =39.806^{\circ}\)
30) \(\left \langle 2,-5 \right \rangle\)
31) \(\left \langle -4,-6 \right \rangle\)
- Answer
-
\(\left | v \right |=7.211, \theta =236.310^{\circ}\)
32) Given \(u = 3i − 4j\) and \(v = −2i + 3j\), calculate \(u\cdot v\).
33) Given \(u = −i − j\) and \(v = i + 5j\), calculate \(u\cdot v\).
- Answer
-
\(-6\)
34) Given \(u=\left \langle -2,4 \right \rangle\) and \(v=\left \langle -3,1 \right \rangle\)
35) Given \(u=\left \langle -1,6 \right \rangle\) and \(v=\left \langle 6,-1 \right \rangle\)
- Answer
-
\(-12\)
Graphical
For the exercises 36-,38 given \(v\), draw \(v\), \(3v\), and \(\dfrac{1}{2}v\).
36) \(\left \langle 2,-1 \right \rangle\)
37) \(\left \langle -1,4 \right \rangle\)
- Answer
-

38) \(\left \langle -3,-2 \right \rangle\)
For the exercises 39-41, use the vectors shown to sketch \(u + v\), \(u − v\), and \(2u\).
39)
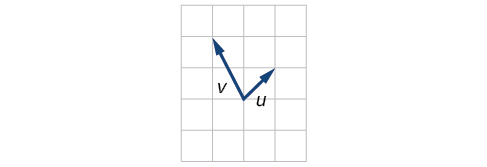
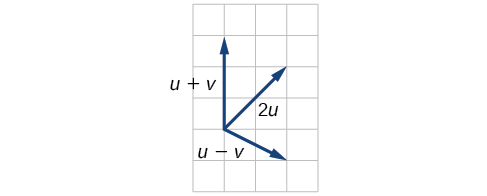
- Answer
-
40)
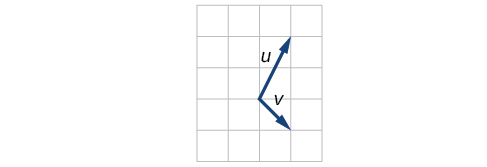
41)
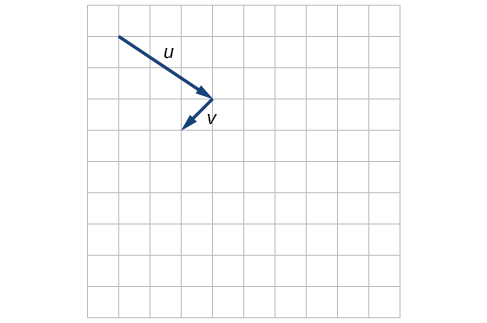
- Answer
-
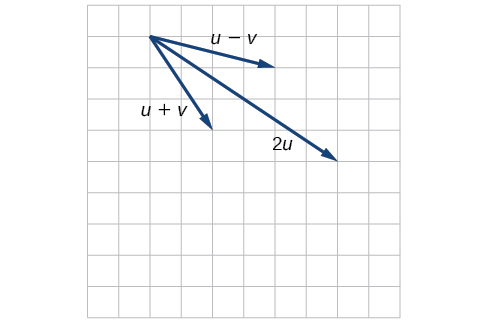
For the exercises 42-43, use the vectors shown to sketch \(2u + v\).
42)
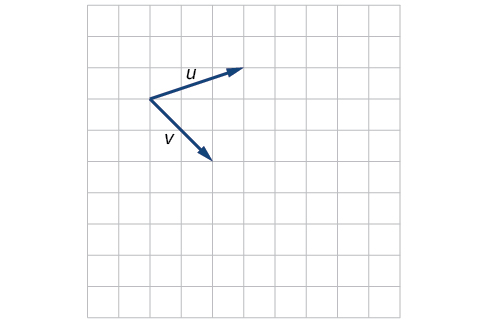
43)
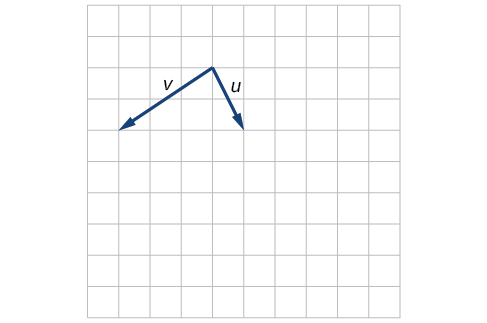
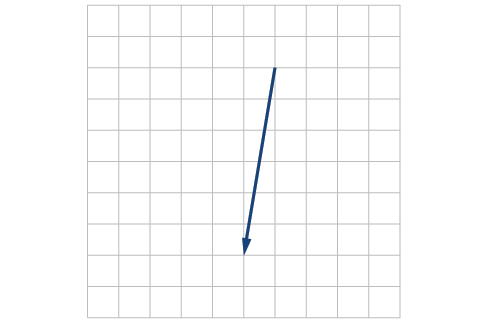
- Answer
-
For the exercises 44-45, use the vectors shown to sketch \(u − 3v\).
44)
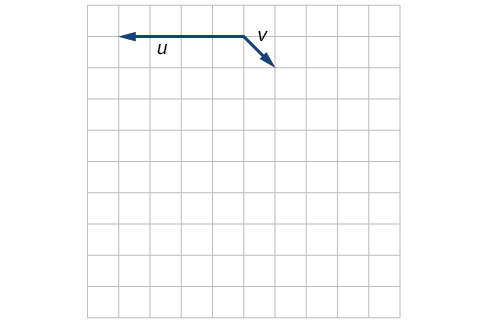
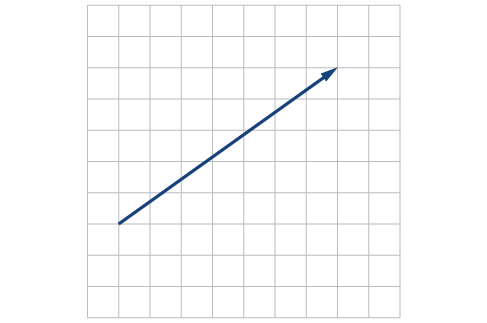
45)
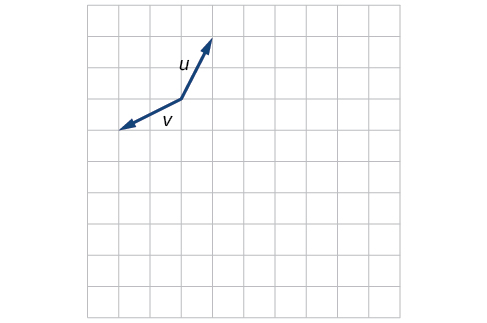
- Answer
-
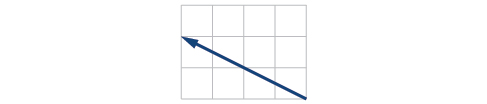
For the exercises 46-47, write the vector shown in component form.
46)
47)
- Answer
-
\(\left \langle 4,1 \right \rangle\)
48) Given initial point \(P_1=(2,1\) and terminal point \(P_2=(-1,2)\)
49) Given initial point \(P_1=(4,-1\) and terminal point \(P_2=(-3,2)\), write the vector \(v\) in terms of \(i\) and \(j\). Draw the points and the vector on the graph.
- Answer
-
\(v=-7i+3j\)
50) Given initial point \(P_1=(3,3\) and terminal point \(P_2=(-3,3)\), write the vector \(v\) in terms of \(i\) and \(j\). Draw the points and the vector on the graph.
Extensions
For the exercises 51-54, use the given magnitude and direction in standard position, write the vector in component form.
51) \(\left | v \right |=6, \theta =45^{\circ}\)
- Answer
-
\(3\sqrt{2}i+3\sqrt{2}j\)
52) \(\left | v \right |=8, \theta =220^{\circ}\)
53) \(\left | v \right |=2, \theta =300^{\circ}\)
- Answer
-
\(i-\sqrt{3}j\)
54) \(\left | v \right |=5, \theta =135^{\circ}\)
55) A \(60\)-pound box is resting on a ramp that is inclined \(12^{\circ}\). Rounding to the nearest tenth,
- Find the magnitude of the normal (perpendicular) component of the force.
- Find the magnitude of the component of the force that is parallel to the ramp.
- Answer
-
- \(58.7\)
- \(12.5\)
56) A \(25\)-pound box is resting on a ramp that is inclined \(8^{\circ}\). Rounding to the nearest tenth,
- Find the magnitude of the normal (perpendicular) component of the force.
- Find the magnitude of the component of the force that is parallel to the ramp.
57) Find the magnitude of the horizontal and vertical components of a vector with magnitude \(8\) pounds pointed in a direction of \(27^{\circ}\) above the horizontal. Round to the nearest hundredth.
- Answer
-
\(x=7.13\) pounds, \(y=3.63\) pounds
58) Find the magnitude of the horizontal and vertical components of the vector with magnitude \(4\) pounds pointed in a direction of \(127^{\circ}\) above the horizontal. Round to the nearest hundredth.
59) Find the magnitude of the horizontal and vertical components of a vector with magnitude \(5\) pounds pointed in a direction of \(55^{\circ}\) above the horizontal. Round to the nearest hundredth.
- Answer
-
\(x=2.87\) pounds, \(y=4.10\) pounds
60) Find the magnitude of the horizontal and vertical components of the vector with magnitude \(1\) pound pointed in a direction of \(8^{\circ}\) above the horizontal. Round to the nearest hundredth.
Real-World Applications
61) A woman leaves home and walks \(3\) miles west, then \(2\) miles southwest. How far from home is she, and in what direction must she walk to head directly home?
- Answer
-
\(4.635\) miles, \(17.764^{\circ}\) N of E
62) A boat leaves the marina and sails \(6\) miles north, then \(2\) miles northeast. How far from the marina is the boat, and in what direction must it sail to head directly back to the marina?
63) A man starts walking from home and walks \(4\) miles east, \(2\) miles southeast, \(5\) miles south, \(4\) miles southwest, and \(2\) miles east. How far has he walked? If he walked straight home, how far would he have to walk?
- Answer
-
\(17\) miles, \(10.318\) miles
64) A woman starts walking from home and walks \(4\) miles east, \(7\) miles southeast, \(6\) miles south, \(5\) miles southwest, and \(3\) miles east. How far has she walked? If she walked straight home, how far would she have to walk?
65) A man starts walking from home and walks \(3\) miles at \(20^{\circ}\) north of west, then \(5\) miles at \(10^{\circ}\) west of south, then \(4\) miles at \(15^{\circ}\) north of east. If he walked straight home, how far would he have to the walk, and in what direction?
- Answer
-
Distance: \(2.868\), Direction: \(86.474^{\circ}\) North of West, or \(3.526^{\circ}\) West of North
66) A woman starts walking from home and walks \(6\) miles at \(40^{\circ}\) north of east, then \(2\) miles at \(15^{\circ}\) east of south, then \(5\) miles at \(30^{\circ}\) south of west. If she walked straight home, how far would she have to walk, and in what direction?
67) An airplane is heading north at an airspeed of \(600\) km/hr, but there is a wind blowing from the southwest at \(80\) km/hr. How many degrees off course will the plane end up flying, and what is the plane’s speed relative to the ground?
- Answer
-
\(4.924^{\circ}\), 659 km/hr
68) An airplane is heading north at an airspeed of \(500\) km/hr, but there is a wind blowing from the northwest at \(50\) km/hr. How many degrees off course will the plane end up flying, and what is the plane’s speed relative to the ground?
69) An airplane needs to head due north, but there is a wind blowing from the southwest at \(60\) km/hr. The plane flies with an airspeed of \(550\) km/hr. To end up flying due north, how many degrees west of north will the pilot need to fly the plane?
- Answer
-
\(4.424^{\circ}\)
70) An airplane needs to head due north, but there is a wind blowing from the northwest at \(80\) km/hr. The plane flies with an airspeed of \(500\) km/hr. To end up flying due north, how many degrees west of north will the pilot need to fly the plane?
71) As part of a video game, the point \((5,7)\) is rotated counterclockwise about the origin through an angle of \(35^{\circ}\). Find the new coordinates of this point.
- Answer
-
\((0.081,8.602)\)
72) As part of a video game, the point \((7,3)\) is rotated counterclockwise about the origin through an angle of \(40^{\circ}\). Find the new coordinates of this point.
73) Two children are throwing a ball back and forth straight across the back seat of a car. The ball is being thrown \(10\) mph relative to the car, and the car is traveling \(25\) mph down the road. If one child doesn't catch the ball, and it flies out the window, in what direction does the ball fly (ignoring wind resistance)?
- Answer
-
\(21.801^{\circ}\), relative to the car’s forward direction
74) Two children are throwing a ball back and forth straight across the back seat of a car. The ball is being thrown \(8\) mph relative to the car, and the car is traveling \(45\) mph down the road. If one child doesn't catch the ball, and it flies out the window, in what direction does the ball fly (ignoring wind resistance)?
75) A \(50\)-pound object rests on a ramp that is inclined \(19^{\circ}\). Find the magnitude of the components of the force parallel to and perpendicular to (normal) the ramp to the nearest tenth of a pound.
- Answer
-
parallel: \(16.28\), perpendicular: \(47.28\) pounds
76) Suppose a body has a force of \(10\) pounds acting on it to the right, \(25\) pounds acting on it upward, and \(5\) pounds acting on it \(45^{\circ}\) from the horizontal. What single force is the resultant force acting on the body?
77) Suppose a body has a force of \(10\) pounds acting on it to the right, \(25\) pounds acting on it ─\(135^{\circ}\) from the horizontal, and \(5\) pounds acting on it directed \(150^{\circ}\) from the horizontal. What single force is the resultant force acting on the body?
- Answer
-
\(19.35\) pounds, \(231.54^{\circ}\) from the horizontal
78) The condition of equilibrium is when the sum of the forces acting on a body is the zero vector. Suppose a body has a force of \(2\) pounds acting on it to the right, \(5\) pounds acting on it upward, and \(3\) pounds acting on it \(45^{\circ}\) from the horizontal. What single force is needed to produce a state of equilibrium on the body?
79) Suppose a body has a force of \(3\) pounds acting on it to the left, \(4\) pounds acting on it upward, and \(2\) pounds acting on it \(30^{\circ}\) from the horizontal. What single force is needed to produce a state of equilibrium on the body? Draw the vector.
- Answer
-
\(5.1583\) pounds, \(75.8^{\circ}\) from the horizontal
Contributors and Attributions
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.


