9.R: Systems of Equations and Inequalities (Review)
- Page ID
- 18812
9.1: Systems of Linear Equations: Two Variables
For the exercises 1-2, determine whether the ordered pair is a solution to the system of equations.
1) \(\begin{align*} 3x-y &= 4\\ x+4y &= -3 \end{align*}\; \; \text{ and }\; (-1,1)\)
- Answer
-
No
2) \(\begin{align*} 6x-2y &= 24\\ -3x+3y &= 18 \end{align*}\; \; \text{ and }\; (9,15)\)
For the exercises 3-5, use substitution to solve the system of equations.
3) \(\begin{align*} 10x+5y &= -5\\ 3x-2y &= -12 \end{align*}\)
- Answer
-
\((-2,3)\)
4) \(\begin{align*} \dfrac{4}{7}x+\dfrac{1}{5}y &= \dfrac{43}{70}\\ \dfrac{5}{6}x-\dfrac{1}{3}y &= -\dfrac{2}{3} \end{align*}\)
5) \(\begin{align*} 5x+6y &= 14\\ 4x+8y &= 8 \end{align*}\)
- Answer
-
\((4,-1)\)
For the exercises 6-8, use addition to solve the system of equations.
6) \(\begin{align*} 3x+2y &= -7\\ 2x+4y &= 6 \end{align*}\)
7) \(\begin{align*} 3x+4y &= 2\\ 9x+12y &= 3 \end{align*}\)
- Answer
-
No solutions exist.
8) \(\begin{align*} 8x+4y &= 2\\ 6x-5y &= 0.7 \end{align*}\)
For the exercises 9-10, write a system of equations to solve each problem. Solve the system of equations.
9) A factory has a cost of production \(C(x)=150x+15,000\) and a revenue function \(R(x)=200x\). What is the break-even point?
- Answer
-
\((300,60,000)\)
10) A performer charges \(C(x)=50x+10,000\), where \(x\) is the total number of attendees at a show. The venue charges \(\$75\) per ticket. After how many people buy tickets does the venue break even, and what is the value of the total tickets sold at that point?
- Answer
-
\((400,30,000)\)
9.2: Systems of Linear Equations: Three Variables
For the exercises 1-8, solve the system of three equations using substitution or addition.
1) \(\begin{align*} 0.5x-0.5y &= 10\\ -0.2y+0.2x &= 4\\ 0.1x+0.1z &= 2 \end{align*}\)
- Answer
-
\((10,-10,10)\)
2) \(\begin{align*} 5x+3y-z &= 5\\ 3x-2y+4z &= 13\\ 4x+3y+5z &= 22 \end{align*}\)
3) \(\begin{align*} x+y+z &= 1\\ 2x+2y+2z &= 1\\ 3x+3y &= 2 \end{align*}\)
- Answer
-
No solutions exist.
4) \(\begin{align*} 2x-3y+z &= -1\\ x+y+z &= -4\\ 4x+2y-3z &= 33 \end{align*}\)
5) \(\begin{align*} 3x+2y-z &= -10\\ x-y+2z &= 7\\ -x+3y+z &= -2 \end{align*}\)
- Answer
-
\((-1,-2,3)\)
6) \(\begin{align*} 3x+4z &= -11\\ x-2y &= 5\\ 4y-z &= -10 \end{align*}\)
7) \(\begin{align*} 2x-3y+z &= 0\\ 2x+4y-3z &= 0\\ 6x-2y-z &= 0 \end{align*}\)
- Answer
-
\(\left (x, \dfrac{8x}{5}, \dfrac{14x}{5} \right )\)
8) \(\begin{align*} 6x-4y-2z &= 2\\ 3x+2y-5z &= 4\\ 6y-7z &= 5 \end{align*}\)
For the exercises 9-10, write a system of equations to solve each problem. Solve the system of equations.
9) Three odd numbers sum up to \(61\). The smaller is one-third the larger and the middle number is \(16\) less than the larger. What are the three numbers?
- Answer
-
\(11, 17, 33\)
10) A local theatre sells out for their show. They sell all \(500\) tickets for a total purse of \(\$8,070.00\). The tickets were priced at \(\$15\) for students, \(\$12\) for children, and \(\$18\) for adults. If the band sold three times as many adult tickets as children’s tickets, how many of each type was sold?
9.3: Systems of Nonlinear Equations and Inequalities: Two Variables
For the exercises 1-5, solve the system of nonlinear equations.
1) \(\begin{align*} y &= x^2 - 7\\ y &= 5x-13 \end{align*}\)
- Answer
-
\((2,−3),(3,2)\)
2) \(\begin{align*} y &= x^2 - 4\\ y &= 5x+10 \end{align*}\)
3) \(\begin{align*} x^2 + y^2 &= 16\\ y &= x-8 \end{align*}\)
- Answer
-
No solution
4) \(\begin{align*} x^2 + y^2 &= 25\\ y &= x^2 + 5 \end{align*}\)
5) \(\begin{align*} x^2 + y^2 &= 4\\ y - x^2 &= 3 \end{align*}\)
- Answer
-
No solution
For the exercises 6-7, graph the inequality.
6) \(y>x^2 - 1\)
7) \(\dfrac{1}{4}x^2 + y^2 < 4\)
- Answer
-
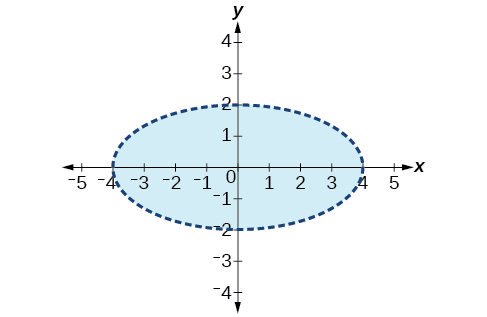
For the exercises 8-10, graph the system of inequalities.
8) \(\begin{align*} x^2 + y^2 +2x &<3 \\ y &>-x^2 - 3 \end{align*}\)
9) \(\begin{align*} x^2 -2x + y^2 - 4x &< 4\\ y &<-x+4 \end{align*}\)
- Answer
-
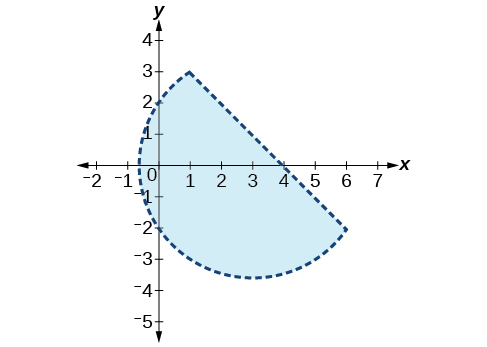
10) \(\begin{align*} x^2 + y^2 &< 1\\ y^2 &< x \end{align*}\)
9.4: Partial Fractions
For the exercises 1-8, decompose into partial fractions.
1) \(\dfrac{-2x+6}{x^2 +3x+2}\)
- Answer
-
\(\dfrac{2}{x+2}, \dfrac{-4}{x+1}\)
2) \(\dfrac{10x+2}{4x^2 +4x+1}\)
3) \(\dfrac{7x+20}{x^2 +10x+25}\)
- Answer
-
\(\dfrac{7}{x+5}, \dfrac{-15}{(x+5)^2}\)
4) \(\dfrac{x-18}{x^2 -12x+36}\)
5) \(\dfrac{-x^2 +36x + 70}{x^3 -125}\)
- Answer
-
\(\dfrac{3}{x-5}, \dfrac{-4x+1}{x^2 +5x+25}\)
6) \(\dfrac{-5x^2 +6x-2}{x^3 +27}\)
7) \(\dfrac{x^3 -4x^2 +3x+11}{(x^2 -2)^2}\)
- Answer
-
\(\dfrac{x-4}{(x^2 -2)}, \dfrac{5x+3}{(x^2 -2)^2}\)
8) \(\dfrac{4x^4 -2x^3 +22x^2 -6x+48}{x(x^2 +4)^2}\)
9.5: Matrices and Matrix Operations
For the exercises 1-12, perform the requested operations on the given matrices.
\[A=\begin{bmatrix} 4 & -2\\ 1 & 3 \end{bmatrix}, \begin{bmatrix} 6 & 7 & -3\\ 11 & -2 & 4 \end{bmatrix}, C=\begin{bmatrix} 6 & 7\\ 11 & -2\\ 14 & 0 \end{bmatrix} D=\begin{bmatrix} 1 & -4 & 9\\ 10 & 5 & -7\\ 2 & 8 & 5 \end{bmatrix} E=\begin{bmatrix} 7 & -14 & 3\\ 2 & -1 & 3\\ 0 & 1 & 9 \end{bmatrix} \nonumber\]
1) \(-4A\)
- Answer
-
\(\begin{bmatrix} -16 & 8\\ -4 & -12 \end{bmatrix}\)
2) \(10D-6E\)
3) \(B+C\)
- Answer
-
undefined; dimensions do not match
4) \(AB\)
5) \(BA\)
- Answer
-
undefined; inner dimensions do not match
6) \(BC\)
7) \(CB\)
- Answer
-
\(\begin{bmatrix} 113 & 28 & 10\\ 44 & 81 & -41\\ 84 & 98 & -42 \end{bmatrix}\)
8) \(DE\)
9) \(ED\)
- Answer
-
\(\begin{bmatrix} -127 & -74 & 176\\ -2 & 11 & 40\\ 28 & 77 & 38 \end{bmatrix}\)
10) \(EC\)
11) \(CE\)
- Answer
-
undefined; inner dimensions do not match
12) \(A^3\)
9.6: Solving Systems with Gaussian Elimination
For the exercises 1-2, write the system of linear equations from the augmented matrix. Indicate whether there will be a unique solution.
1) \(\left [ \begin{array}{ccc|c} 1 & 0 & -3 & 7 \\ 0 & 1 & 2 & -5\\ 0 & 0 & 0 & 0\\ \end{array} \right ]\)
- Answer
-
\(\begin{align*} x-3z &= 7\\ y+2z &= -5 \end{align*}\; \; \text{with infinite solutions}\)
2) \(\left [ \begin{array}{ccc|c} 1 & 0 & 5 & -9 \\ 0 & 1 & -2 & 4\\ 0 & 0 & 0 & 3\\ \end{array} \right ]\)
For the exercises 3-5, write the augmented matrix from the system of linear equations.
3) \(\begin{align*} -2x+2y+z &= 7\\ 2x-8y+5z &= 0\\ 19x-10y+22z &= 3 \end{align*}\)
- Answer
-
\(\left [ \begin{array}{ccc|c} -2 & 2 & 1 & 7 \\ 2 & -8 & 5 & 0\\ 19 & -10 & 22 & 3\\ \end{array} \right ]\)
4) \(\begin{align*} 4x+2y-3z &= 14\\ -12x+3y+z &= 100\\ 9x-6y+2z &= 31 \end{align*}\)
5) \(\begin{align*} x+3z &= 12\\ -x+4y &= 0\\ y+2z &= -7 \end{align*}\)
- Answer
-
\(\left [ \begin{array}{ccc|c} 1 & 0 & 3 & 12 \\ -1 & 4 & 0 & 0\\ 0 & 1 & 2 & -7\\ \end{array} \right ]\)
For the exercises 6-10, solve the system of linear equations using Gaussian elimination.
6) \(\begin{align*} 3x-4y &= -7\\ -6x+8y &= 14 \end{align*}\)
7) \(\begin{align*} 3x-4y &= 1\\ -6x+8y &= 6 \end{align*}\)
- Answer
-
No solutions exist.
8) \(\begin{align*} -1.1x-2.3y &= 6.2\\ -5.2x-4.1y &= 4.3 \end{align*}\)
9) \(\begin{align*} 2x+3y+2z &= 1\\ -4x-6y-4z &= -2\\ 10x+15y+10z &= 0 \end{align*}\)
- Answer
-
No solutions exist.
10) \(\begin{align*} -x+2y-4z &= 8\\ 3y+8z &= -4\\ -7x+y+2z &= 1 \end{align*}\)
9.7: Solving Systems with Inverses
For the exercises 1-4, find the inverse of the matrix.
1) \(\begin{bmatrix} -0.2 & 1.4\\ 1.2 & -0.4 \end{bmatrix}\)
- Answer
-
\(\dfrac{1}{8}\begin{bmatrix} 2 & 7\\ 6 & 1 \end{bmatrix}\)
2) \(\begin{bmatrix} \frac{1}{2} & -\frac{1}{2}\\ -\frac{1}{4} & \frac{3}{4} \end{bmatrix}\)
3) \(\begin{bmatrix} 12 & 9 & -6\\ -1 & 3 & 2\\ -4 & -3 & 2 \end{bmatrix}\)
- Answer
-
No inverse exists.
4) \(\begin{bmatrix} 2 & 1 & 3\\ 1 & 2 & 3\\ 3 & 2 & 1 \end{bmatrix}\)
For the exercises 5-8, find the solutions by computing the inverse of the matrix.
5) \(\begin{align*} 0.3x-0.1y &= -10\\ -0.1x+0.3y &= 14 \end{align*}\)
- Answer
-
\((-20,40)\)
6) \(\begin{align*} 0.4x-0.2y &= -0.6\\ -0.1x+0.05y &= 0.3 \end{align*}\)
7) \(\begin{align*} 4x+3y-3z &= -4.3\\ 5x-4y-z &= -6.1\\ x+z &= -0.7 \end{align*}\)
- Answer
-
\((-1, 0.2, 0.3)\)
8) \(\begin{align*} -2x-3y+2z &= 3\\ -x+2y+4z &= -5\\ -2y+5z &= -3 \end{align*}\)
For the exercises 9-10, write a system of equations to solve each problem. Solve the system of equations.
9) Students were asked to bring their favorite fruit to class. \(90\%\) of the fruits consisted of banana, apple, and oranges. If oranges were half as popular as bananas and apples were \(5\%\) more popular than bananas, what are the percentages of each individual fruit?
- Answer
-
\(17\%\) oranges, \(34\%\) bananas, \(39\%\) apples
10) A sorority held a bake sale to raise money and sold brownies and chocolate chip cookies. They priced the brownies at \(\$2\) and the chocolate chip cookies at \(\$1\). They raised \(\$250\) and sold \(175\) items. How many brownies and how many cookies were sold?
9.8: Solving Systems with Cramer's Rule
For the exercises 1-4, find the determinant.
1) \(\begin{vmatrix} 100 & 0\\ 0 & 0 \end{vmatrix}\)
- Answer
-
\(0\)
2) \(\begin{vmatrix} 0.2 & -0.6\\ 0.7 & -1.1 \end{vmatrix}\)
3) \(\begin{vmatrix} -1 & 4 & 3\\ 0 & 2 & 3\\ 0 & 0 & -3 \end{vmatrix}\)
- Answer
-
\(6\)
4) \(\begin{vmatrix} \sqrt{2} & 0 & 0\\ 0 & \sqrt{2} & 0\\ 0 & 0 & \sqrt{2} \end{vmatrix}\)
For the exercises 5-10, use Cramer’s Rule to solve the linear systems of equations.
5) \(\begin{align*} 4x-2y &= 23\\ -5x-10y &= -35 \end{align*}\)
- Answer
-
\(\left(6, \dfrac{1}{2} \right)\)
6) \(\begin{align*} 0.2x-0.1y &= 0\\ -0.3x+0.3y &= 2.5 \end{align*}\)
7) \(\begin{align*} -0.5x+0.1y &= 0.3\\ -0.25x+0.05y &= 0.15 \end{align*}\)
- Answer
-
\(x, 5x+3\)
8) \(\begin{align*} x+6y+3z &= 4\\ 2x+y+2z &= 3\\ 3x-2y+z &= 0 \end{align*}\)
9) \(\begin{align*} 4x-3y+5z &= -\dfrac{5}{2}\\ 7x-9y-3z &= \dfrac{3}{2}\\ x-5y-5z &= \dfrac{5}{2} \end{align*}\)
- Answer
-
\(\left(0, 0, -\dfrac{1}{2} \right)\)
10) \(\begin{align*} \dfrac{3}{10}x-\dfrac{1}{5}y-\dfrac{3}{10}z &= -\dfrac{1}{50}\\ \dfrac{1}{10}x-\dfrac{1}{10}y-\dfrac{1}{2}z &= -\dfrac{9}{50}\\ \dfrac{2}{5}x-\dfrac{1}{2}y-\dfrac{3}{5}z &= -\dfrac{1}{5} \end{align*}\)
Practice Test
1) Is the following ordered pair a solution to the system of equations? \[\begin{align*} -5x-y &= 12 \text{ with } (-3,3)\\ x+4y &= 9 \end{align*} \nonumber \]
- Answer
-
Yes
For the exercises 2-9, solve the systems of linear and nonlinear equations using substitution or elimination. Indicate if no solution exists.
2) \(\begin{align*} \dfrac{1}{2}x-\dfrac{1}{3}y &= 4\\ \dfrac{3}{2}x-y &= 0 \end{align*}\)
3) \(\begin{align*} -\dfrac{1}{2}x-4y &= 4\\ 2x+16y &= 2 \end{align*}\)
- Answer
-
No solutions exist.
4) \(\begin{align*} 5x-y &= 1\\ -10x+2y &= -2 \end{align*}\)
5) \(\begin{align*} 4x-6y-2z &= \dfrac{1}{10}\\ x-7y+5z &= -\dfrac{1}{4}\\ 3x+6y-9z &= \dfrac{6}{5} \end{align*}\)
- Answer
-
\(\dfrac{1}{20} (10, 5, 4)\)
6) \(\begin{align*} x+z &= 20\\ x+y+z &= 20\\ x+2y+z &= 10 \end{align*}\)
7) \(\begin{align*} 5x-4y-3z &= 0\\ 2x+y+2z &= 0\\ x-6y-7z &= 0 \end{align*}\)
- Answer
-
\(\left ( x, \dfrac{16x}{5} - \dfrac{13x}{5} \right )\)
8) \(\begin{align*} y &= x^2 +2x-3\\ y &= x-1 \end{align*}\)
9) \(\begin{align*} y^2 + x^2 &= 25\\ y^2 -2x^2 &= 1 \end{align*}\)
- Answer
-
\((-2\sqrt{2}, -\sqrt{17}), (-2\sqrt{2}, \sqrt{17}), (2\sqrt{2}, -\sqrt{17}), (2\sqrt{2}, \sqrt{17})\)
For the exercises 10-11, graph the following inequalities.
10) \(y < x^2 + 9\)
11) \(\begin{align*} x^2 + y^2 &> 4 \\ y &< x^2 + 1 \end{align*}\)
- Answer
-
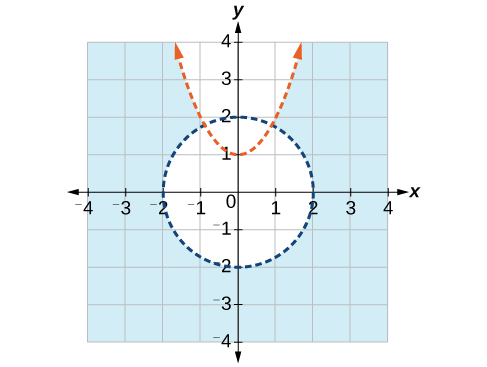
For the exercises 12-14, write the partial fraction decomposition.
12) \(\dfrac{-8x-30}{x^2 + 10x+25}\)
13) \(\dfrac{13x+2}{(3x+1)^2}\)
- Answer
-
\(\dfrac{5}{3x+1}-\dfrac{2x+3}{(3x+1)^2}\)
14) \(\dfrac{x^4 - x^3 +2x-1}{x(x^2+1)^2}\)
For the exercises 15-21, perform the given matrix operations.
15) \(5\begin{bmatrix} 4 & 9\\ -2 & 3 \end{bmatrix}+\dfrac{1}{2} \begin{bmatrix} -6 & 12\\ 4 & -8 \end{bmatrix}\)
- Answer
-
\(\begin{bmatrix} 17 & 51\\ -8 & 11 \end{bmatrix}\)
16) \(\begin{bmatrix} 1 & 4 & -7\\ -2 & 9 & 5\\ 12 & 0 & -4 \end{bmatrix} \begin{bmatrix} 3 & -4\\ 1 & 3\\ 5 & 10 \end{bmatrix}\)
17) \(\begin{bmatrix} \frac{1}{2} & \frac{1}{3}\\ \frac{1}{4} & \frac{1}{5} \end{bmatrix} ^{-1}\)
- Answer
-
\(\begin{bmatrix} 12 & -20\\ -15 & 30 \end{bmatrix}\)
18) \(\textbf{det}\begin{vmatrix} 0 & 0\\ 400 & 4,000 \end{vmatrix}\)
19) \(\textbf{det}\begin{vmatrix} \frac{1}{2} & -\frac{1}{2} & 0\\ -\frac{1}{2} & 0 & \frac{1}{2}\\ 0 & \frac{1}{2} & 0 \end{vmatrix}\)
- Answer
-
\(-\dfrac{1}{8}\)
20) If \(\textbf{det}(A)=-6\), what would be the determinant if you switched rows 1 and 3, multiplied the second row by \(12\), and took the inverse?
21) Rewrite the system of linear equations as an augmented matrix. \[\begin{align*} 14x-2y-13z &= 140\\ -2x+3y-6z &= -1\\ x-5y+12z &= 11 \end{align*} \nonumber\]
- Answer
-
\(\left [ \begin{array}{ccc|c} 14 & -2 & 13 & 140 \\ -2 & 3 & -6 & -1\\ 1 & -5 & 12 & 11\\ \end{array} \right ]\)
22) Rewrite the augmented matrix as a system of linear equations. \[\left [ \begin{array}{ccc|c} 1 & 0 & 3 & 12 \\ -2 & 4 & 9 & -5\\ -6 & 1 & 2 & 8\\ \end{array} \right ] \nonumber\]
For the exercises 23-24, use Gaussian elimination to solve the systems of equations.
23) \(\begin{align*} x-6y &= 4\\ 2x-12y &= 0 \end{align*}\)
- Answer
-
No solutions exist.
24) \(\begin{align*} 2x+y+z &= -3\\ x-2y+3z &= 6\\ x-y-z &= 6 \end{align*}\)
For the exercises 25-26, use the inverse of a matrix to solve the systems of equations.
25) \(\begin{align*} 4x-5y &= -50\\ -x+2y &= 80 \end{align*}\)
- Answer
-
\((100, 90)\)
26) \(\begin{align*} \dfrac{1}{100}x-\dfrac{3}{100}y+\dfrac{1}{20}z &= -49\\ \dfrac{3}{100}x-\dfrac{7}{100}y-\dfrac{1}{100}z &= 13\\ \dfrac{9}{100}x-\dfrac{9}{100}y-\dfrac{9}{100}z &= 99 \end{align*}\)
For the exercises 27-28, use Cramer’s Rule to solve the systems of equations.
27) \(\begin{align*} 200x-300y &= 2\\ 400x+715y &= 4 \end{align*}\)
- Answer
-
\(\left (\dfrac{1}{100}, 0 \right )\)
28) \(\begin{align*} 0.1x+0.1y-0.1z &= -1.2\\ 0.1x-0.2y+0.4z &= -1.2\\ 0.5x-0.3y+0.8z &= -5.9 \end{align*}\)
For the exercises 29-30, solve using a system of linear equations.
29) A factory producing cell phones has the following cost and revenue functions: \(C(x)=x^2+75x+2,688\) and \(R(x)=x^2+160x\). What is the range of cell phones they should produce each day so there is profit? Round to the nearest number that generates profit.
- Answer
-
\(32\) or more cell phones per day
30) A small fair charges \(\$1.50\) for students, \(\$1\) for children, and \(\$2\) for adults. In one day, three times as many children as adults attended. A total of \(800\) tickets were sold for a total revenue of \(\$1,050\). How many of each type of ticket was sold?
Contributors and Attributions
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.


