Skip to main content
Mathematics LibreTexts

3.3: Exercises

  1. Last updated
  2. Save as PDF
  • Page ID
    48963

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    Exercise \(\PageIndex{1}\)

    For each of the following functions,

    1. \(f(x)=3x+1\)
    2. \(f(x)=x^2-x\)
    3. \(f(x)=\sqrt{x^2-9}\)
    4. \(f(x)=\frac{1}{x}\)
    5. \(f(x)=\frac{x-5}{x+2}\)
    6. \(f(x)=-x^3\)

    calculate the function values

    1. \(f(3)\)
    2. \(f(5)\)
    3. \(f(-2)\)
    4. \(f(0)\)
    5. \(f(\sqrt{13})\)
    6. \(f(\sqrt{2}+3)\)
    7. \(f(-x)\)
    8. \(f(x+2)\)
    9. \(f(x)+h\)
    10. \(f(x+h)\)
    Answer
      1. \(10\)
      2. \(16\)
      3. \(-5\)
      4. \(1\)
      5. \(3 \sqrt{13}+1\)
      6. \(3 \sqrt{2}+10\)
      7. \(-3 x+1\)
      8. \(3 x+7\)
      9. \(3 x+1+h\)
      10. \(3 x+3 h+1\)
      1. \(6\)
      2. \(20\)
      3. \(6\)
      4. \(0\)
      5. \(13-\sqrt{13}\)
      6. \(8+5 \sqrt{2}\)
      7. \(x^{2}+x\)
      8. \(x^{2}+3 x+2\)
      9. \(x^{2}-x+h\)
      10. \(x^{2}+2 x h+h^{2}-x-h\)
      1. \(0\)
      2. \(4\)
      3. undefined
      4. undefined
      5. \(2\)
      6. \(\sqrt{2+6 \sqrt{2}}\)
      7. \(\sqrt{x^{2}-9}\)
      8. \(\sqrt{x^{2}+4 x-5}\)
      9. \(\sqrt{x^{2}-9}+h\)
      10. \(\sqrt{x^{2}+2 x h+h^{2}-9}\)
      1. \(\dfrac{1}{3}\)
      2. \(\dfrac{1}{5}\)
      3. \(-\dfrac{1}{2}\)
      4. undefined
      5. \(\dfrac{\sqrt{13}}{13}\)
      6. \(\dfrac{3-\sqrt{2}}{7}\)
      7. \(-\dfrac{1}{x}\)
      8. \(\dfrac{1}{x+2}\)
      9. \(\dfrac{1+x h}{x}\)
      10. \(\dfrac{1}{x+h}\)
      1. \(\dfrac{-2}{5}\)
      2. \(0\)
      3. undefined
      4. \(\dfrac{-5}{2}\)
      5. \(\dfrac{\sqrt{13}-5}{\sqrt{13}+2}=\dfrac{23-7 \sqrt{13}}{9}\)
      6. \(\dfrac{\sqrt{2}-2}{\sqrt{2}+5}=\dfrac{-12+7 \sqrt{2}}{23}\)
      7. \(\dfrac{-x-5}{-x+2}\)
      8. \(\dfrac{x-3}{x+4}\)
      9. \(\dfrac{x-5+h x+2 h}{x+2}\)
      10. \(\dfrac{x+h-5}{x+h+2}\)
      1. \(-27\)
      2. \(-125\)
      3. \(8\)
      4. \(0\)
      5. \(-\sqrt{2197}\)
      6. \(-45-29 \sqrt{2}\)
      7. \(x^{3}\)
      8. \(f(x+2)=-(x+2)^{3}\) or in descending order \(f(x+2)=-x^{3}-6 x^{2}-12 x-8\)
      9. \(-x^{3}+h\)
      10. \(-(x+h)^{3}\) or \(-x^{3}-3 x^{2} h-3 x h^{2}-h^{3}\)

    Exercise \(\PageIndex{2}\)

    Let \(f\) be the piecewise defined function

    \[f(x)=\left\{ \begin{matrix} x-5 & \text{, for}& -4<x< 3 \\ x^2 & \text{, for}& 3\leq x\leq 6 \end{matrix} \right. \nonumber \]

    1. State the domain of the function.

    Find the function values

    1. \(f(2)\)
    2. \(f(5)\)
    3. \(f(-3)\)
    4. \(f(3)\)
    Answer
    1. \(D=(-4,6]\)
    2. \(-3\)
    3. \(25\)
    4. \(-8\)
    5. \(9\)

    Exercise \(\PageIndex{3}\)

    Let \(f\) be the piecewise defined function

    \[f(x)=\left\{ \begin{matrix} |x|-x^2 & \text{, for}& x< 2 \\ 7 & \text{, for}& 2\leq x< 5 \\ x^2-4x+1 & \text{, for} & 5< x \end{matrix} \right. \nonumber \]

    1. State the domain of the function.

    Find the function values

    1. \(f(1)\)
    2. \(f(-2)\)
    3. \(f(3)\)
    4. \(f(2)\)
    5. \(f(5)\)
    6. \(f(7)\)
    Answer
    1. \(D=(-\infty, 5) \cup(5, \infty)\), or, alternatively, \(D=\mathbb{R}-\{5\}\)
    2. \(0\)
    3. \(-2\)
    4. \(7\)
    5. \(7\)
    6. undefined
    7. \(22\)

    Exercise \(\PageIndex{4}\)

    Find the difference quotient \(\dfrac{f(x+h)-f(x)}{h}\) for the following functions:

    1. \(f(x)=5x\)
    2. \(f(x)=2x-6\)
    3. \(f(x)=x^2\)
    4. \(f(x)=x^2+5x\)
    5. \(f(x)=x^2+3x+4\)
    6. \(f(x)=3-x^2\)
    7. \(f(x)=x^2+4x-9\)
    8. \(f(x)=3x^2-2x+7\)
    9. \(f(x)=x^3\)
    Answer
    1. \(5\)
    2. \(2\)
    3. \(2 x+h\)
    4. \(2 x+5+h\)
    5. \(2 x+3+h\)
    6. \(-2 x-h\)
    7. \(2 x+4+h\)
    8. \(6 x-2+3 h\)
    9. \(3 x^{2}+3 x h+h^{2}\)

    Exercise \(\PageIndex{5}\)

    Find the difference quotient \(\dfrac{f(x)-f(a)}{x-a}\) for the following functions:

    1. \(f(x)=3x\)
    2. \(f(x)=4x-7\)
    3. \(f(x)=x^2-3x\)
    4. \(f(x)=\dfrac{1}{x}\)
    Answer
    1. \(3\)
    2. \(4\)
    3. \(x+a-3\)
    4. \(\dfrac{-1}{a x}\)

    Exercise \(\PageIndex{6}\)

    Find the domains of the following functions.

    1. \(f(x)=x^2+3x+5\)
    2. \(f(x)=|x-2|\)
    3. \(f(x)=\sqrt{x-2}\)
    4. \(f(x)=\sqrt{8-2x}\)
    5. \(f(x)=\sqrt{|x+3|}\)
    6. \(f(x)=\dfrac{1}{x+6}\)
    7. \(f(x)=\dfrac{x-5}{x-7}\)
    8. \(f(x)=\dfrac{x+1}{x^2-7x+10}\)
    9. \(f(x)=\dfrac{x}{|x-2|}\)
    10. \(f(x)= \begin{cases}|x| & \text { for } 1<x<2 \\ 2 x & \text { for } 3 \leq x\end{cases}\)
    11. \(f(x)=\dfrac{\sqrt{x}}{x-9}\)
    12. \(f(x)=\dfrac{5}{\sqrt{x+4}}\)
    Answer
    1. \(D=\mathbb{R}\) all real numbers
    2. \(D=\mathbb{R}\)
    3. \(D=[2, \infty)\)
    4. \(D=(-\infty, 4]\)
    5. \(D=\mathbb{R}\)
    6. \(D=\mathbb{R}-\{-6\}\)
    7. \(D=\mathbb{R}-\{7\}\)
    8. \(D=\mathbb{R}-\{2,5\}\)
    9. \(D=\mathbb{R}-\{2\}\)
    10. \(D=(1,2) \cup[3, \infty)\)
    11. \(D=[0,9) \cup(9, \infty)\)
    12. \(D=(-4, \infty)\)

    Exercise \(\PageIndex{7}\)

    Below are three graphs for the functions \(f\), \(g\), and \(h\).

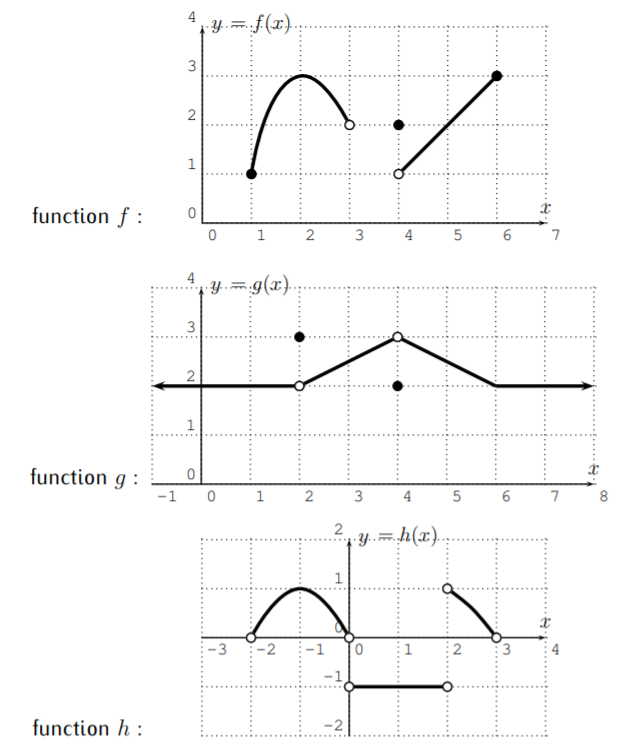
    clipboard_e357281d7371539d367611eb6f194860f.png

    1. Find the domain and range of \(f\).
    2. Find the domain and range of \(g\).
    3. Find the domain and range of \(h\).

    Find the following function values:

    1. \(f(1)\)
    2. \(f(2)\)
    3. \(f(3)\)
    4. \(f(4)\)
    5. \(f(5)\)
    6. \(f(6)\)
    7. \(f(7)\)
    8. \(g(0)\)
    9. \(g(1)\)
    10. \(g(2)\)
    11. \(g(3)\)
    12. \(g(4)\)
    13. \(g(6)\)
    14. \(g(13.2)\)
    15. \(h(-2)\)
    16. \(h(-1)\)
    17. \(h(0)\)
    18. \(h(1)\)
    19. \(h(2)\)
    20. \(h(3)\)
    21. \(h(\sqrt{2})\)
    Answer
    1. domain \(D_{f}=[1,3) \cup[4,6]\) and range \(R_{f}=[1,3]\)
    2. \(D_{g}=\mathbb{R}\) and \(R_{g}=[2,3]\)
    3. \(D_{h}=(-2,0) \cup(0,2) \cup(2,3)\) and \(R_{h}=\{-1\} \cup(0,1]\)
    4. \(1\)
    5. \(3\)
    6. undefined
    7. \(2\)
    8. \(2\)
    9. \(3\)
    10. undefined
    11. \(2\)
    12. \(2\)
    13. \(3\)
    14. \(2.5\)
    15. \(2\)
    16. \(2\)
    17. \(2\)
    18. undefined
    19. \(1\)
    20. undefined
    21. \(-1\)
    22. undefined
    23. undefined
    24. \(-1\)

    Exercise \(\PageIndex{8}\)

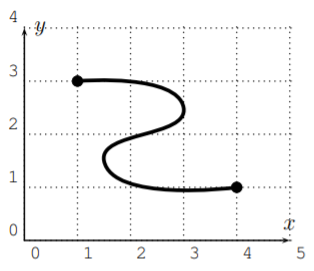
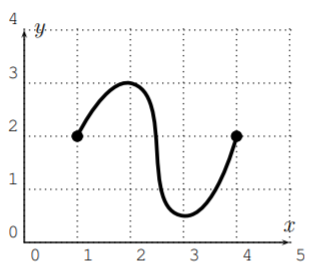
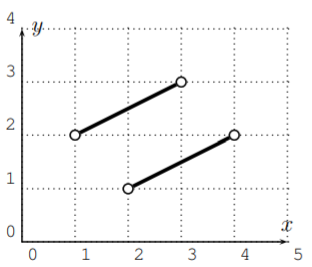
    Use the vertical line test to determine which of the following graphs are the graphs of functions?

    1. clipboard_e01c9b5cdc69b21e91ca337e91789cd95.png
    2. clipboard_e55e0164990bb9c8429617ddde82f6553.png
    3. clipboard_edb2b720df9b9f9ae9f1c89e8ed9cfbb1.png
    4. clipboard_e855824720648b8780cf7eee010c0b111.png
    Answer
    1. not a function
    2. this is a function
    3. not a function
    4. not a function

    Exercise \(\PageIndex{9}\)

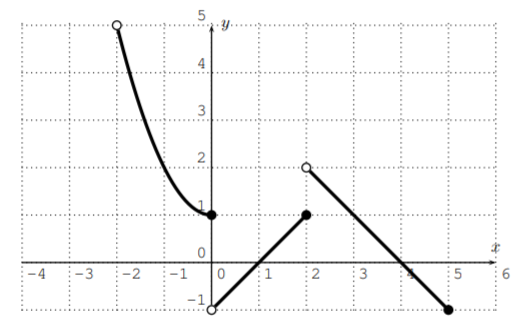
    Let \(f\) be the function given by the following graph.

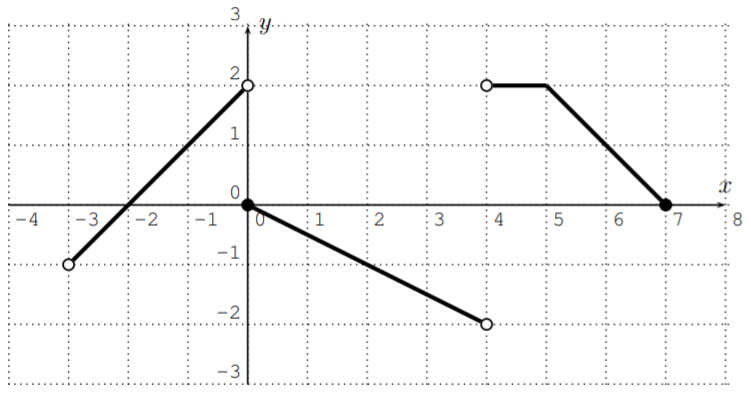
    clipboard_e255b5a52aafa856630204e40870c3073.png

    1. What is the domain of \(f\)?
    2. What is the range of \(f\)?
    3. For which \(x\) is \(f(x)=0\)?
    4. For which \(x\) is \(f(x)=2\)?
    5. For which \(x\) is \(f(x)\leq 1\)?
    6. For which \(x\) is \(f(x)> 0\)?
    7. Find \(f(2)\) and \(f(5)\).
    8. Find \(f(2)+f(5)\).
    9. Find \(f(2)+5\).
    10. Find \(f(2+5)\).
    Answer
    1. \(D=(-3,4) \cup(4,7]\)
    2. \(R=(-2,2]\)
    3. \(x=-2\) or \(x=0\) or \(x=7\)
    4. \(x \in(4,5]\)
    5. \(x \in(-3,-1] \cup[0,4) \cup[6,7]\)
    6. \(x \in(-2,0) \cup(4,7)\)
    7. \(f(2)=-1\), \(f(5)=2\)
    8. \(f(2)+f(5)=1\)
    9. \(f(2)+5=4\)
    10. \(f(2+5)=0\)

    Exercise \(\PageIndex{10}\)

    The graph below displays the number of students admitted to a college during the years 1995 to 2007.

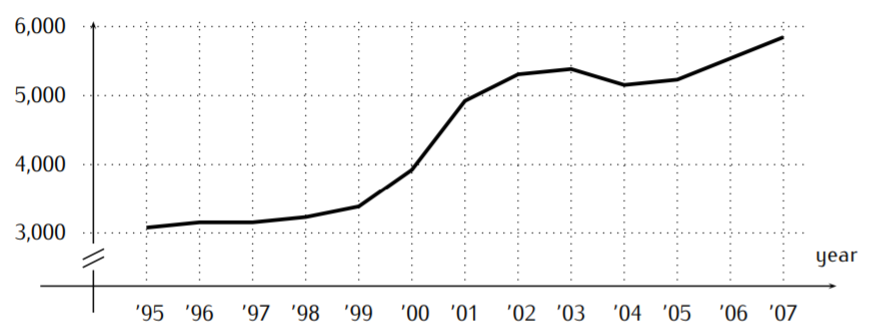
    clipboard_e06ef0d4fc3ad4b62b1f05cc7a61b8e87.png

    1. How many students were admitted in the year 2000?
    2. In what years were the most students admitted?
    3. In what years did the number of admitted students rise fastest?
    4. In what year(s) did the number of admitted students decline?
    Answer
    1. Approximately 3,900 students were admitted in the year 2000
    2. The most students were admitted in 2007
    3. In 2000, the number of admitted students rose fastest.
    4. In 2003 the number of admitted students declined.

    Exercise \(\PageIndex{11}\)

    Consider the function described by the following formula:

    \[f(x)=\left\{ \begin{matrix} x^2+1 & \text{, for}& -2< x\leq 0 \\ x-1 & \text{, for}& 0<x\leq 2 \\ -x+4 & \text{, for} & 2<x\leq 5 \end{matrix} \right. \nonumber \]

    What is the domain of the function \(f\)? Graph the function \(f\).

    Answer

    domain \(D=(-2,5]\)

    graph:

    clipboard_eb3e7986e38bd1172af3b9fa33a35092d.png

    This page titled 3.3: Exercises is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Thomas Tradler and Holly Carley (New York City College of Technology at CUNY Academic Works) via source content that was edited to the style and standards of the LibreTexts platform.