23.1: Introduction to Sequences and Series

Definition: Word

A sequence is an ordered list of numbers. We write a sequence in order as follows: \[a_1, a_2, a_3, a_4, \dots\]

In short we write the above sequence as \(\{a_n\}\) or \(\{a_n\}_{n\geq 1}\).

Note

You might wonder how this topic fits into the general theme of functions. We can alternatively define a sequence \(a\) to be a function \(a: \mathbb{N} \rightarrow R\), where the domain is all natural numbers, and the range \(R\) is a subset of the real or complex numbers. We write the \(n\)th term of the sequence as \(a_n=a(n)\).

Example \(\PageIndex{1}\)

Here are some examples of sequences.

1. \(4, 6, 8, 10, 12, 14, 16, 18, \dots\)
2. \(1, 3, 9, 27, 81, 243, \dots\)
3. \(+5, -5, +5, -5, +5, -5, \dots\)
4. \(1, 1, 2, 3, 5, 8, 13, 21, 34, 55, \dots\)
5. \(5, 8, -12, 4, 5.3, 7, -3, \sqrt{2}, 18, \dfrac{2}{3}, 9, \dots\)

For many of these sequences we can find rules that describe how to obtain the individual terms. For example, in (a), we always add the fixed number \(2\) to the previous number to obtain the next, starting from the first term \(4\). This is an example of an arithmetic sequence, and we will study those in more detail in section 23.2.

In (b), we start with the first element \(1\) and multiply by the fixed number \(3\) to obtain the next term. This is an example of a geometric sequence, and we will study those in more detail in chapter 24.

The sequence in (c) alternates between \(+5\) and \(-5\), starting from \(+5\). Note, that we can get from one term to the next by multiplying \((-1)\) to the term. Therefore, this is another example of a geometric sequence.

The sequence in (d) is called the Fibonacci sequence. In the Fibonacci sequence, each term is calculated by adding the previous two terms, starting with the first two terms \(1\) and \(1\):

\[1+1=2, \quad 1+2=3, \quad 2+3=5, \quad 3+5=8, \quad 5+8=13, \quad \dots \nonumber \]

Finally, the sequence in (e) does not seem to have any obvious rule by which the terms are generated.

In many cases, the sequence is given by a formula for the \(n\)th term \(a_n\).

Example \(\PageIndex{2}\)

Consider the sequence \(\{a_n\}\) with \(a_n=4n+3\). We can calculate the individual terms of this sequence:

\(\begin{array}{lll}
\text { first term: } & a_{1}= & 4 \cdot 1+3=7 \\
\text { second term: } & a_{2}= & 4 \cdot 2+3=11 \\
\text { third term: } & a_{3}= & 4 \cdot 3+3=15 \\
\text { fourth term: } & a_{4}= & 4 \cdot 4+3=19 \\
\text { fifth term: } & a_{5}= & 4 \cdot 5+3=23 \\
& \vdots &
\end{array} \)

Thus, the sequence is: \(7, 11, 15, 19, 23, 27, 31, 35, \dots\)

Furthermore, from the formula, we can directly calculate a higher term, for example the \(200\)th term is given by:

\[\quad\,\,\, 200\text{th term: }\quad\, a_{200}=\,\, 4\cdot 200+3 = 803 \nonumber \]

Example \(\PageIndex{3}\)

Find the first \(6\) terms of each sequence.

1. \(a_n=n^2\)
2. \(a_n=\dfrac{n}{n+1}\)
3. \(a_n=(-1)^n\)
4. \(a_n=(-1)^{n+1}\cdot 2^n\)

Solution

1. We can easily calculate the first \(6\) terms of \(a_n=n^2\) directly:

\[1, 4, 9, 16, 25, 36, \dots \nonumber \]

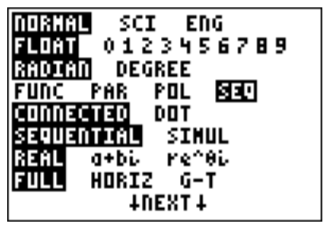
We can also use the calculator to produce the terms of a sequence. To this end, we switch the calculator from function mode to sequence mode in the mode menu (press \(\boxed{\text{mode}}\)):

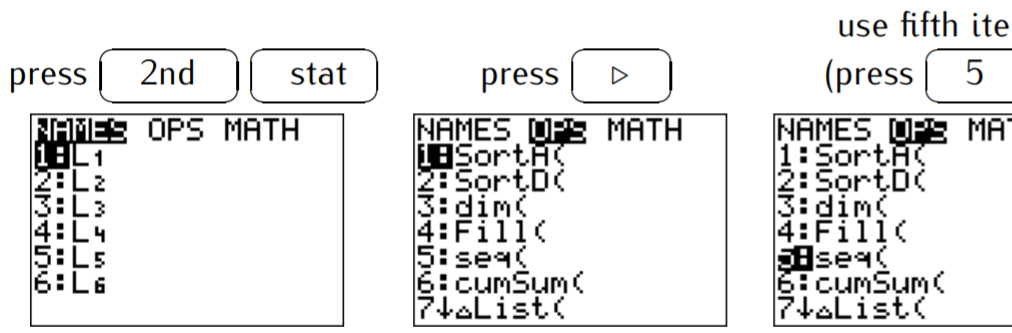
To enter the sequence, we need to use the LIST menu (press \(\boxed{\text{2nd}}\) and then \(\boxed{\text{stat}}\)), then go to the OPS menu (press \(\boxed{\triangleright }\)), and use the fifth item (press \(\boxed{\text{5}}\)):

For the sequence, we need to specify four pieces of information, where the index \(n\) can be entered via the \(\boxed{X, T, \theta, n}\) key.

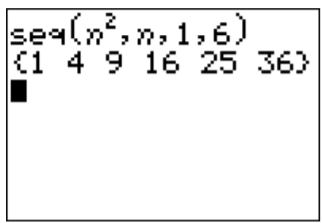
1st entry is the given formula for \(a_{n}=n^{2}\)

2nd entry is the index \(n\) of the sequence \(a_{n}\)

3rd and 4th entries are the first and last index 1 and 6 of the wanted sequence, here: \(a_{1}, \ldots, a_{6}\)

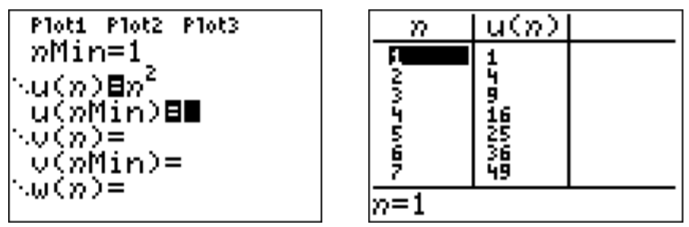
Alternatively, we can enter the function in the \(\boxed{y=}\) menu, starting from the first index \(n=1\), and with \(n\)th term given by \(a_n=n^2\). The values of the sequence are displayed in the table window (press \(\boxed{\text{2nd}}\) and \(\boxed{\text{graph}}\)).

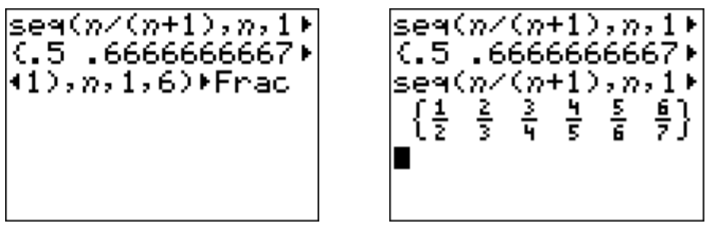
2. We calculate the lowest terms of \(a_n=\dfrac{n}{n+1}\):

\[a_1=\dfrac{1}{1+1}=\dfrac{1}{2}, \quad a_2=\dfrac{2}{2+1}=\dfrac{2}{3}, \quad a_3=\dfrac{3}{3+1}=\dfrac{3}{4}, \quad \dots \nonumber \]

Identifying the pattern, we can simply write \(a_1,\dots, a_6\) as follows:

\[\dfrac{1}{2}, \dfrac{2}{3}, \dfrac{3}{4}, \dfrac{4}{5}, \dfrac{5}{6}, \dfrac{6}{7} \nonumber \]

We can also use the calculator to find the sequence:

Note

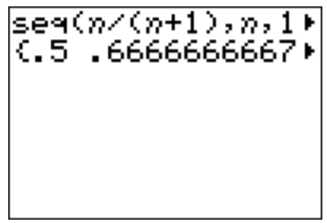
Fractions can be displayed with the calculator by adding “Frac” to it from the MATH menu (using and the top item). For example, the fraction \(\dfrac 2 7\) is displayed below without approximation.

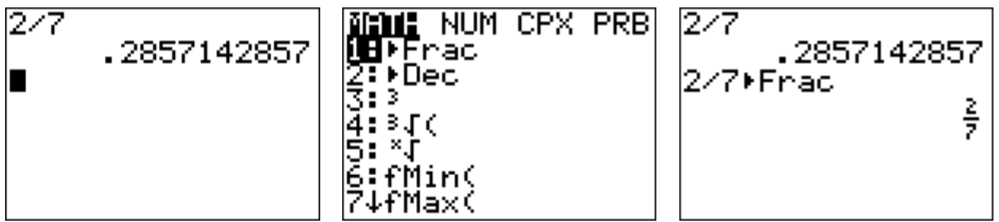
Adding “Frac” to the sequence displays it more appropriately as a sequence of fractions.

3. Since \((-1)^n\) is \(+1\) for even \(n\), but is \(-1\) for odd \(n\), the sequence \(a_n=(-1)^n\) is:

\[-1,+1,-1,+1,-1,+1 \nonumber \]

4. Similar to part (c), \((-1)^{n+1}\) is \(-1\) for even \(n\), and is \(+1\) for odd \(n\). This, together with the calculation \(2^1=2, 2^2=4, 2^3=8, 2^4=16\), etc., we get the first six terms of the sequence:

\[+2, -4, +8, -16, +32, -64 \nonumber \]

Another way to describe a sequence is by giving a recursive formula for the \(n\)th term \(a_n\) in terms of the lower terms. Here are some examples.

Example \(\PageIndex{4}\)

Find the first \(6\) terms in the sequence described below.

1. \(a_1=4\), and \(a_n=a_{n-1}+5\) for \(n>1\)
2. \(a_1=3\), and \(a_n=2\cdot a_{n-1}\) for \(n>1\)
3. \(a_1=1\), \(a_2=1\), and \(a_n=a_{n-1}+a_{n-2}\) for \(n>2\)

Solution

1. The first term is explicitly given as \(a_1=4\). Then, we can calculate the following terms via \(a_n=a_{n-1}+5\):

\[\begin{aligned} a_2 & = a_1+ 5= 4+5 =9 \\ a_3 & = a_2+ 5= 9+5 =14 \\ a_4 & = a_3+ 5= 14+5 =19 \\ a_5 & = a_4+ 5= 19+5 =24 \\ & \vdots &\end{aligned} \nonumber \]

2. We have \(a_1=3\), and calculate \(a_2=2\cdot a_1=2\cdot 3=6\), \(a_3=2\cdot a_2=2\cdot 6=12\), \(a_4=2\cdot a_3=2\cdot 12=24\), etc. We see that the effect of the recursive relation \(a_n=2\cdot a_{n-1}\) is to double the previous number. The sequence is:

\[3, 6, 12, 24, 48, 96, 192, \dots \nonumber \]

3. Starting from \(a_1=1\), and \(a_2=1\), we can calculate the higher terms:

\[\begin{aligned} a_3 & = a_1+ a_2= 1+1 =2 \\ a_4 & = a_2+ a_3= 1+2 =3 \\ a_5 & = a_3+ a_4= 2+3 =5 \\ a_6 & = a_4+ a_5= 3+5 =8 \\ & \vdots &\end{aligned} \nonumber \]

Studying the sequence for a short while, we see that this is precisely the Fibonacci sequence from example 23.1.1 (d).

Note

There is no specific reason for using the indexing variable \(n\) in the sequence \(\{a_n\}\). Indeed, we may use as well any other variable. For example, if the sequence \(\{a_n\}_{n\geq 1}\) is given by the formula \(a_n=4n+3\), then we can also write this as \(a_k=4k+3\) or \(a_i=4i+3\). In particular, the sequences \(\{a_n\}_{n\geq 1}=\{a_k\}_{k\geq 1}=\{a_i\}_{i\geq 1}=\{a_j\}_{j\geq 1}\) are all identical as sequences.

We will be concerned with the task of adding terms in a sequence, such as \(a_1+a_2+a_3+\dots+a_k\), for which we will use a standard summation notation.

Definition: Series

A series is a sum of terms in a sequence. We denote the sum of the first \(k\) terms in a sequence with the following notation:

\[\sum_{i=1}^k a_i = a_1+a_2+\dots + a_k\]

The summation symbol “\(\sum\)” comes from the greek letter \(\Sigma\), pronounced “sigma,” which is the greek letter for “S.”

Note

More generally, we denote the sum from the \(j\)th to the \(k\)th term (where \(j\leq k\)) in a sequence with the following notion:

\[\sum_{i=j}^k a_i = a_j+a_{j+1}+\dots + a_k \nonumber \]

Furthermore, the term \(\sum\limits_{i=j}^k a_i\) is sometimes also written in the form \(\sum\nolimits_{i=j}^k a_i\).

Example \(\PageIndex{5}\)

Find the sum.

1. \(\sum_{i=1}^4 a_i, \text{ for } a_i=7i +3\)
2. \(\sum_{j=1}^6 a_j, \text{ for } a_n=(-2)^n\)
3. \(\sum_{k=1}^5 \left(4+k^2\right)\)

Solution

1. The first four terms \(a_1, a_2, a_3, a_4\) of the sequence \(\{a_i\}_{i\geq 1}\) are:

\[10, 17, 24, 31 \nonumber \]

The sum is therefore:

\[\sum_{i=1}^4 a_i=a_1+a_2+a_3+a_4=10+17+24+31=82 \nonumber \]

We may also find the answer with the calculator. Before entering the sequence (via \(\boxed{\text{2nd}} \boxed{\text{stat}} \boxed{\triangleright } \boxed{\text{5}}\) as in example 23.1.4 (a) above), we have to put a sum symbol in the LIST menu and MATH submenu (with \(\boxed{\text{2nd}} \boxed{\text{stat}} \boxed{\triangleleft} \boxed{\text{5}}\)):

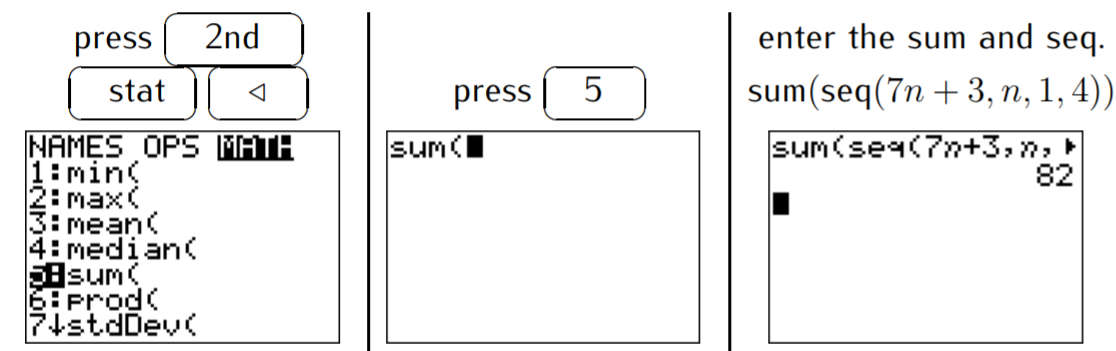
2. The first six terms of \(\{a_n\}\) with \(a_n=(-2)^n\) are:

\[(-2)^1=-2, \, (-2)^2=4, \,(-2)^3=-8, \, (-2)^4=16, \, (-2)^5=-32, \, (-2)^6=64 \nonumber \]

We calculate \(\sum_{j=1}^6 a_j\) by adding these first six terms. (Note that the sum is independent of the index \(j\) appearing in the sum \(\sum_{j=1}^6 a_j\), which we could as well replace by any other index \(\sum_{j=1}^6 a_j=\sum_{k=1}^6 a_k\), etc.) We get:

\[\begin{aligned} \sum_{j=1}^6 a_j &= a_1+a_2+a_3+a_4+a_5+a_6 \\ &= (-2)+4+(-8)+16+(-32)+64 = 42 \end{aligned} \nonumber \]

3. For the sum \(\sum_{k=1}^5 \left(4+k^2\right)\) we need to add the first four terms of the sequence \(a_k=4+k^2\). Calculating and adding the terms of this sequence, we obtain the sum:

\[\begin{aligned} \sum_{k=1}^5 \left(4+k^2\right) &= (4+1^2)+(4+2^2)+(4+3^2)+(4+4^2)+(4+5^2) \\ &= (4+1)+(4+4)+(4+9)+(4+16)+(4+25) \\ &= 5+8+13+20+29 \\ &= 75\end{aligned} \nonumber \]

This answer can of course also be confirmed with the calculator (after replacing the index \(k\) with \(n\)) as we did in part (a).