8.2: Density
- Page ID
- 7694
If we are comparing two populations, and we note that there are many actors in one that are not connected to any other ("isolates"), and in the other population most actors are embedded in at least one dyad - we would likely conclude that social life is very different in the two populations.
Measuring the density of a network gives use a ready index of the degree of dyadic connection in a population. For binary data, density is simply the ratio of the number of adjacencies that are present divided by the number of pairs - what proportion of all possible dyadic connections are actually present. If we have measured the ties among actors with values (strengths, closeness, probabilities, etc.) density is usually defined as the sum of the values of all ties divided by the number of possible ties. That is, with valued data, density is usually defined as the average strength of ties across all possible (not all actual) ties. Where the data are symmetric or undirected, density is calculated relative to the number of unique pairs \(\left( \left( n * n - 1 \right) / 2 \right)\); where the data are directed, density is calculated across the total number of pairs.
Network>Cohesion>Density is a useful tool for calculating the density of whole populations, or of partitions. A typical dialog is shown in Figure 8.1.
Figure 8.1: Dialog of Network>Cohesion>Density
In this dialog, we are again examining the Knoke information tie network. We have used an attribute or partition to divide the cases into three sub-populations (governmental agencies, non-governmental generalist, and welfare specialists) so that we can see the amount of connection within and between groups. This is done by creating a separate attribute data file (or a column in such a file), with the same row labels, and scores for each case on the "partitioning" variable. Partitioning is not necessary to calculate density. The results of the analysis are shown in Figure 8.2.
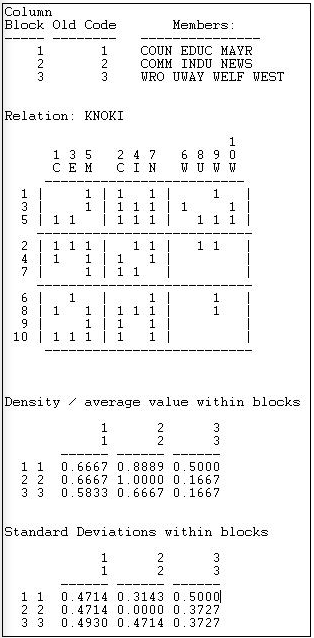
Figure 8.2: Density of three sub-populations in Knoke information network
After providing a map of the partitioning, a blocked (partitioned) matrix is provided showing the values of the connections between each pair of actors. Next, the within-block densities are presented. The density in the 1,1 block is 0.6667. That is, of the six possible directed ties among actors 1, 3, and 5, four are actually present (we have ignored the diagonal - which is the most common approach). We can see that the three sub-populations appear to have some differences. Governmental agencies (block 1) have quite dense in and out ties to one another, and to the other populations; non-governmental generalists (block 2) have out-ties among themselves and with block 1, and have high densities of in-ties with all three sub-populations. The welfare specialists have high density of information sending to the other two blocks (but not within their block), and receive more input from governmental than from non-governmental organizations.
The extent to which these simple characterizations of blocks characterize all the individuals within those blocks - essentially the validity of the blocking - can be assessed by looking at the standard deviations within the partitions. The standard deviations measure the lack of homogeneity within the partition, or the extent to which the actors vary.
A social structure in which individuals were highly clustered would display a pattern of high densities on the diagonal, and low densities elsewhere.


