8.7: Krackhardt's Graph Theoretical Dimensions of Hierarchy
- Page ID
- 9109
Embedding of actors in dyads, triads, neighborhoods, clusters, and groups are all ways in which the social structure of a population may display "texture". All of these forms of embedding structures speak to the issue of the "horizontal differentiation" of the population - separate, but not necessarily ranked or unequal groupings.
A very common form of embedding of actors in structures, though, does involve unequal rankings. Hierarchies, in which individuals or sub-populations are not only differentiated, but also ranked, are extremely common in social life. The degree of hierarchy in a population speaks to the issue of "vertical differentiation".
While we all have an intuitive sense of what it means for a structure to be a hierarchy, most would agree that structures can be "more or less" hierarchical. It is necessary to be quite precise about the meaning of the term if we are going to build indexes to measure the degree of hierarchy.
Krackhardt (1994) provided an elegant definition of the meaning of hierarchy, and developed measures of each of the four component dimensions of the concept that he identified. Krackhardt defines a pure, "ideal typical" hierarchy as an "out-tree" graph. An out-tree graph is a directed graph in which all points are connected, and all but one node (the "boss") has an in-degree of one. This means that all actors in the graph (except the ultimate "boss") have a single superior node. The simplest "hierarchy" is a directed line graph A to B to C to D... More complex hierarchies may have wider, and varying "spans of control" (out-degrees of points).
This very simple definition of the pure type of hierarchy can be deconstructed into four individually necessary and jointly sufficient conditions. Krackhardt develops index numbers to assess the extent to which each of the four dimensions deviates from the pure ideal type of an out-tree, and hence develops four measures of the extent to which a given structure resembles the ideal typical hierarchy.
1) Connectedness: To be a pure out-tree, a graph must be connected into a single component - all actors are embedded in the same structure. We can measure the extent to which this is not true by looking at the ratio of the number of pairs in the directed graph that are reachable relative to the number of ordered pairs. That is, what proportion of actors cannot be reached by other actors? Where a graph has multiple components - multiple un-connected sub-populations - the proportion not reachable can be high. If all the actors are connected in the same component, if there is a "unitary" structure, the graph is more hierarchical.
2) Hierarchy: To be a pure out-tree, there can be no reciprocated ties. Reciprocal relations between two actors imply equal status, and this denies pure hierarchy. We can assess the degree of deviation from pure hierarchy by counting the number of pairs that have reciprocated ties relative to the number of pairs where there is any tie; that is, what proportion of all tied pairs have reciprocated ties.
3) Efficiency: To be a pure out-tree each node must have an in-degree of one. That is, each actor (except the ultimate boss) has a single boss. This aspect of the ideal type is termed "efficiency" because structures with multiple bosses have unnecessary redundant communication of orders from superiors to subordinates. The amount of deviation from this aspect of the pure out-tree can be measured by counting the difference between the actual number of links (minus 1, since the ultimate boss has no boss) and the maximum possible number of links. The bigger the difference, the greater the inefficiency. This dimension then measures the extent to which actors have a "single boss".
4) Least upper bound (LUB): To be a pure out-tree, each pair of actors (except pairs formed between the ultimate boss and others) must have an actor that directs ties to both - that is, command must be unified. The deviation of a graph from this condition can be measured by counting the numbers of pairs of actors that do not have a common boss relative to the number of pairs that could (which depends on the number of actors and the span of control of the ultimate boss).
The Network>Network Properties>Krackhardt GTD algorithms calculate indexes of each of the four dimensions, where higher scores indicate greater hierarchy. Figure 8.13 shows the results for the Knoke information network.
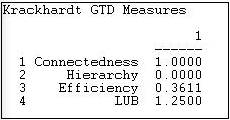
Figure 8.13: Output of Network>Network Properties>Krackhardt GTD for Knoke information network
The information network does form a single component, as there is at least one actor that can reach all others. So, the first dimension of pure hierarchy - that all the actors be embedded in a single structure - is satisfied. The ties in the information exchange network, though, are very likely to be reciprocal (at least insofar as they can be, given the limitations of the density). There are a number of nodes that receive information from multiple others, so the network is not "efficient". The least upper bound measure (the extent to which all actors have a boss in common) reports a value of 1.25, which would appear to be out of range and, frankly, is a puzzle.

