6.9: Discontinuous Forcing

Last updated
Save as PDF

Page ID: 388

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

In the last section we looked at the Heaviside function its Laplace transform. Now we will use this tool to solve differential equations.

Example $\PageIndex{1}$

A 1 kg bar is attached to a spring with spring constant 5 and damping constant 2. It is pulled down 3 inches from it equilibrium position and the released. After one second a constant force of 10 Newtons is exerted on the bar. The force remains turned on indefinitely. Determine the equation of motion of the bar.

Solution

We have the differential equation

\[ y'' + 2y' + 5y = 10u_1(t)\]

with

\[ y(0) = 3 \]

\[ y'(0) = 0 .\]

We solve this by the method of Laplace transforms. We have

\[ \begin{align} L\{y''\} + 2L\{y'\} + 5L\{y\} &= 10L\{u_1(t)\} \\ \implies s^2L\{y\} - 3s - 0 + 2(sL\{y\} - 3) + 5L\{y\} &= 10e^{-s} /s \\ \implies (s^2 + 2s + 5)L\{y\} - 3s - 6 &= 10e^{-s} /s \\ \implies L\{y\} &= \dfrac{3s + 6 }{s^2 + 2s + 5} + \dfrac{10 }{s(s^2 + 2s + 5)} . \end{align} \]

We use partial fractions on the second term

\[ \dfrac{10}{s(s^2 + 2s + 4)} = \dfrac{A}{s} + \dfrac{Bs+C}{s^2+2s+5} \]

\[ A(s^2 + 2s + 5) + (Bs + C)s = 10 \]

\[ (A + B)s^2 + (2A + C)s + 5A = 10 \]

The constant term gives

$ A =2 $

Thus

$ B = -2 $ $C = -4 $

We can complete the square

\[ s^2 + 2s + 5 = (s+1)^2 +4 \]

Putting all the algebra together we get

\[ \begin{align*} L\{y\} &= \dfrac{3s + 6}{(s + 1)^2 + 4} + e^{-s}\dfrac{2}{s} + e^{-s}\dfrac{-2s - 4}{ (s + 1)^2 + 4 } \\ &= 3\dfrac{s + 1 + 1}{(s + 1)^2 + 4} + e^{-s}\dfrac{2}{s} - 2e^{-s}\dfrac{(s + 1) + 1 }{(s + 1)^2 + 4 } \\ &= 3\dfrac{s + 1}{(s + 1)^2 + 4} + 3/2 \dfrac{2}{(s + 1)^2 + 4} + e^{-s}\dfrac{2}{s} - 2e^{-s}\dfrac{(s + 1) }{(s + 1)^2 + 4 } - e^{-s}\dfrac{2 }{(s + 1)^2 + 4 } \end{align*}\]

Now use the table to take the inverse Laplace transform to get

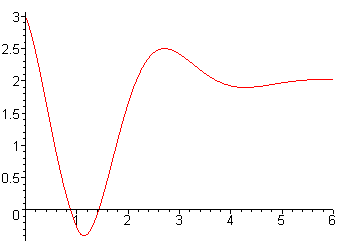
\[ y = 3e^{-t}\cos(2t) + 3/2 e^{-t -1}\sin(2t) + 2u_1 - 2u_1(t)e^{-t +1}\cos(2t - 2) - u_1(t)e^{-t +1} \sin(2t - 2). \]

Below is the graph

$discon2.gif$

Contributors and Attributions

Larry Green (Lake Tahoe Community College)
Integrated by Justin Marshall.