1.6: Lines and Planes
- Page ID
- 598
Lines
Our goal is to come up with the equation of a line given a vector v parallel to the line and a point (a,b,c) on the line. The figure (shown in 2D for simplicity) shows that if P is a point on the line then
\[ \langle x,y \rangle = P + tv\nonumber \]
for some number \(t\).
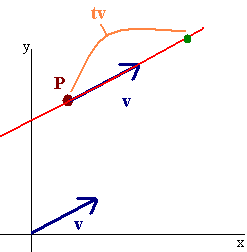
The picture is the same for 3D. The formula is given below.
Parametric Equations of a Line
The parametric equations for the line through the point \((a,b,c)\) and parallel to the vector v are
\[\langle x,y,z\rangle = \langle a,b,c\rangle + t\textbf{v}.\nonumber \]
Example \(\PageIndex{1}\)
Find the parametric equations of the line that passes through the point \((1, 2, 3)\) and is parallel to the vector \(\langle 4, -2, 1\rangle\).
Solution
We write:
\[\langle x, y, z\rangle = \langle 1, 2, 3\rangle + t \langle 4, -2, 1\rangle = \langle 1 + 4t, 2 - 2t, 3 + t\rangle \nonumber \]
or
\[ x(t) = 1 + 4t,\nonumber \]
\[y(t) = 2 - 2t,\nonumber \]
\[z(t) = 3 + t.\nonumber \]
Exercise \(\PageIndex{1}\)
Find the parametric equations of the line through the two points \((2,1,7)\) and \((1,3,5)\).
Hint: a vector parallel to the line has tail at \((2,1,7)\) and head at \((1,3,5)\).
Planes
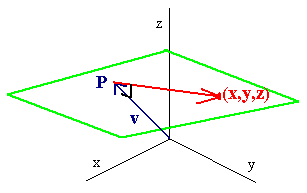
If S is a plane then a vector n is normal (perpendicular) to the plane if it is orthogonal to every vector that lies on the plane. Suppose that n is a normal vector to a plane and \((a,b,c)\) is a point on the plane. Let \((x,y,z)\) be a general point on the plane, then
\[ \langle x - a, y - b, z - c\rangle \nonumber \]
is parallel to the plane, hence
\[\vec{n} \cdot \langle x - a, y - b, z - c\rangle = 0.\nonumber \]
This defines the equation of the plane.
Example \(\PageIndex{2}\)
Find the equation of the plane that contains the point \((2,1,0)\) and has normal vector \(\langle 1,2,3\rangle \).
Solution
We have
\[\langle 1,2,3\rangle \cdot \langle x - 2,y - 1,z - 0\rangle = 0\nonumber \]
so that
\[1(x - 2) + 2(y - 1) + 3z = 0\nonumber \]
or
\[ x + 2y + 3z = 4.\nonumber \]
Example \(\PageIndex{3}\)
Find the equation of the plane through the points
- \(P = (0,0,1)\)
- \(Q = (2,1,0)\)
- \(R = (1,1,1)\)
Solution
Let
\[\textbf{v} = Q-P = \langle 2,1,-1\rangle \nonumber \]
and
\[\textbf{w} = R-P = \langle 1,1,0\rangle \nonumber \]
then to find a vector normal to the plane, we find the cross product of \(v\) and \(w\):
\[v \times w = \begin{vmatrix} \hat{\textbf{i}} & \hat{\textbf{i}} & \hat{\textbf{i}} \\ 2 & 1 &-1 \\ 1 &1 0 \end{vmatrix} = \hat{\textbf{i}} - \hat{\textbf{j}} + \hat{\textbf{k}} \nonumber \]
or
\[\langle 1, -1, 1\rangle .\nonumber \]
We can now use the formula:
\[\langle 1, -1, 1\rangle \cdot \langle x, y, z - 1\rangle = 0\nonumber \]
or
\[x - y + z - 1 = 0\nonumber \]
or
\[x - y + z = 1\nonumber \]
Distance Between a Point and a Plane
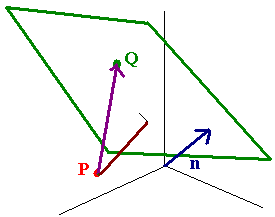
Let P be a point and Q be a point on a plane with normal vector n, then the distance between P and the plane is given by
Distance Between a Point \(P\) and a Plane With Normal Vector n
Let \(Q\) be a point on the plane with normal vector \(\vec{n}\). The the distance from the point \(P\) to this plane is given by
\[ Proj_nPQ = \dfrac{ ||PQ \cdot \vec{n}|| }{ || \vec{n}|| }.\nonumber \]
Example \(\PageIndex{4}\)
Find the distance between the point \((1,2,3)\) and the plane
\[2x - y - 2z = 5.\nonumber \]
Solution
The normal vector can be read off from the equation as
\[\vec{n} = \langle 2, -1, -2\rangle .\nonumber \]
Now find a convenient point on the plane such as \(Q = (0, -5, 0)\). We have
\[Q = \langle -1, -7, -3\rangle \nonumber \]
and
\[ \vec{n} \cdot PQ = -2 + 7 + 6 = 11.\nonumber \]
We find the magnitude of n by taking the square root of the sum of the squares. The sum is
\[4 + 1 + 4 = 9\nonumber \]
so
\[|| \vec{n} || = 3.\nonumber \]
Hence the distance from the point to the plane is \(\frac{11}{3}\).
The Angle Between Two Planes
The angle between two planes is given by the angle between the normal vectors.
Example \(\PageIndex{5}\)
Find the angle between the two planes
\[ 3x - 2y + 5z = 1\nonumber \]
and
\[4x + 2y - z = 4.\nonumber \]
We have the two normal vectors are
\[ \vec{n} = \langle 3,-2,5\rangle \nonumber \]
and
\[\vec{m} = \langle 4,2,-1\rangle .\nonumber \]
We have
\[\vec{n} \cdot \vec{ m} = 3\nonumber \]
\[ || \vec{n} || = \sqrt{38}\nonumber \]
\[ || \vec{m} || = \sqrt{21}\nonumber \]
hence the angle is
\[ \cos^{-1} \left(\dfrac{3}{\sqrt{38}\sqrt{21}} \right) = 1.46 \, rad.\nonumber \]
Contributors and Attributions
- Larry Green (Lake Tahoe Community College)
Integrated by Justin Marshall.


