4.4E: Exercises

Last updated
Save as PDF

Page ID: 18526

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

4.4: Graphs of Logarithmic Functions

Verbal

1) The inverse of every logarithmic function is an exponential function and vice-versa. What does this tell us about the relationship between the coordinates of the points on the graphs of each?

Answer: Since the functions are inverses, their graphs are mirror images about the line $y-x$So for every point $(a,b)$ on the graph of a logarithmic function, there is a corresponding point $(b,a)$ on the graph of its inverse exponential function.

2) What type(s) of translation(s), if any, affect the range of a logarithmic function?

Exercise $\PageIndex{3}$

What type(s) of translation(s), if any, affect the domain of a logarithmic function?

Answer: Shifting the function right or left and reflecting the function about the $y$-axis will affect its domain.

4) Consider the general logarithmic function $f(x)=\log _b(x)$Why can’t $x$ be zero?

5) Does the graph of a general logarithmic function have a horizontal asymptote? Explain.

Answer: No. A horizontal asymptote would suggest a limit on the range, and the range of any logarithmic function in general form is all real numbers.

Algebraic

For the following exercises, state the domain and range of the function.

6) $f(x)=\log _3(x+4)$

Exercise $\PageIndex{7}$

$h(x)=\ln \left ( \dfrac{1}{2}-x \right )$

Answer: Domain: $\left ( -\infty , \dfrac{1}{2} \right )$; Range: $(-\infty , \infty )$

8) $g(x)=\log _5(2x+9)-2$

9) $h(x)=\ln (4x+17)-5$

Answer: Domain: $\left ( -\dfrac{17}{4}, \infty \right )$; Range: $(-\infty , \infty )$

10) $f(x)=\log _2 (12-3x)-3$

For the following exercises, state the domain and the vertical asymptote of the function.

11) $f(x)=\log _b (x-5)$

Answer: Domain: $(5, \infty )$; Vertical asymptote: $x=5$

12) $g(x)=\ln (3-x)$

13) $f(x)=\log (3x+1)$

Answer: Domain: $\left ( -\dfrac{1}{3}, \infty \right )$; Vertical asymptote: $x=-\dfrac{1}{3}$

14) $f(x)=3\log (-x)+2$

15) $g(x)=-\ln (3x+9)-7$

Answer: Domain: $(-3, \infty )$; Vertical asymptote: $x=-3$

For the following exercises, state the domain, vertical asymptote, and end behavior of the function.

16) $f(x)=\ln (2-x)$

17) $f(x)=\log \left ( x-\dfrac{3}{7} \right )$

Answer

Domain: $\left ( \dfrac{3}{7},\infty \right )$

Vertical asymptote: $x=\dfrac{3}{7}$

End behavior: as $x\rightarrow \left (\dfrac{3}{7} \right )^+$, $f(x)\rightarrow -\infty$ and as $x\rightarrow \infty ,f(x)\rightarrow \infty$

18) $h(x)=-\log (3x-4)+3$

Exercise $\PageIndex{19}$

$g(x)=\ln (2x+6)-5$

Answer

Domain: $\left ( -3,\infty \right )$

Vertical asymptote: $x=-3$

End behavior: as $x\rightarrow -3^+$, $f(x)\rightarrow -\infty$ and as $x\rightarrow \infty ,f(x)\rightarrow \infty$

20) $f(x)=\log_3 (15-5x)+6$

For the following exercises, state the domain, range, and x- and y-intercepts, if they exist. If they do not exist, write DNE.

Exercise $\PageIndex{21}$

$h(x)=\log_4 (x-1)+1$

Answer

Domain: $\left (1,\infty \right )$

Range: $-\infty , \infty $

Vertical asymptote: $x=1$

$x$-intercept: $\left ( \dfrac{5}{4},0\right )$

$y$-intercept: DNE

22) $f(x)=\log (5x+10)+3$

23) $g(x)=\ln (-x)-2$

Answer

Domain: $\left (-\infty ,0 \right )$

Range: $-\infty , \infty $

Vertical asymptote: $x=0$

$x$-intercept: $\left ( -e^2,0 \right )$

$y$-intercept: DNE

24) $f(x)=\log_2 (x+2)-5$

25) $h(x)=3\ln (x)-9$

Answer

Domain: $\left (0,\infty \right )$

Range: $-\infty , \infty $

Vertical asymptote: $x=0$

$x$-intercept: $\left ( e^3,0 \right )$

$y$-intercept: DNE

Graphical

For the following exercises, match each function in Figure below with the letter corresponding to its graph.

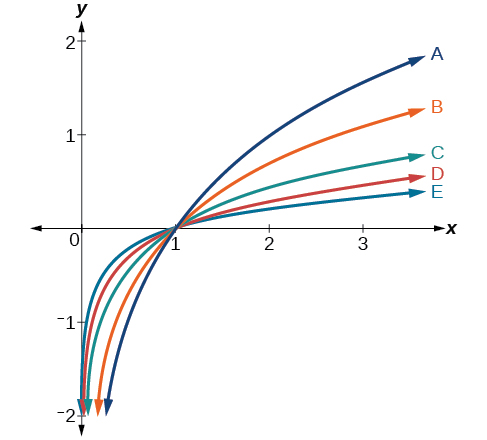
$Ex. 4.4.26.png$

26) $d(x)=\log (x)$

27) $f(x)=\ln (x)$

Answer: $B$

28) $g(x)=\log_2 (x)$

29) $h(x)=\log_5 (x)$

Answer: $C$

30) $j(x)=\log_{25} (x)$

For the following exercises, match each function in Figure with the letter corresponding to its graph.

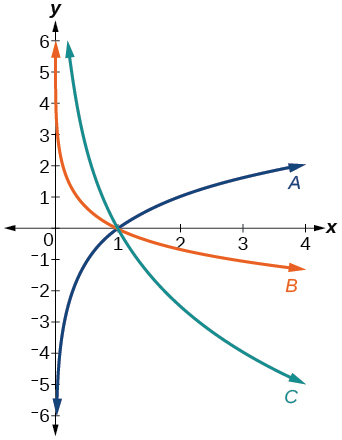
$Ex 4.4.31.png$

31) $f(x)=\log_{\frac{1}{3}} (x)$

Answer: $B$

32) $g(x)=\log_2 (x)$

33) $h(x)=\log_{\frac{3}{4}} (x)$

Answer: $C$

For the following exercises, sketch the graphs of each pair of functions on the same axis.

34) $f(x)=\log (x)$ and $g(x)=10^x$

35) $f(x)=e^x$ and $g(x)=\ln (x)$

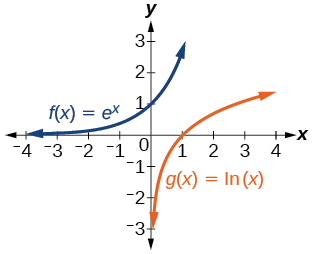
Answer: $Ex 4.4.35.png$

For the following exercises, match each function in Figure with the letter corresponding to its graph.

36) $f(x)=\log _4(-x+2)$

37) $g(x)=-\log _4(x+2)$

Answer: $C$

38) $h(x)=\log _4(x+2)$

For the following exercises, sketch the graph of the indicated function.

39) $f(x)=\log _2(x+2)$

Answer: $Ex 4.4.39.png$

40) $f(x)=2\log (x)$

Exercise $\PageIndex{41}$

$f(x)=\ln (-x)$

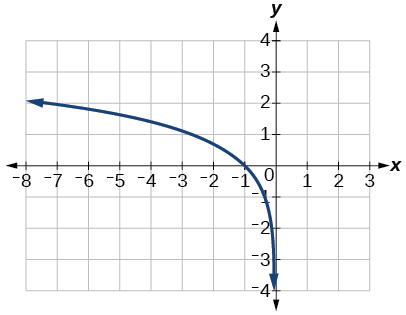
Answer: $Ex 4.4.41.png$

42) $g(x)=\log (4x+16)+4$

43) $g(x)=\log (6-3x)+1$

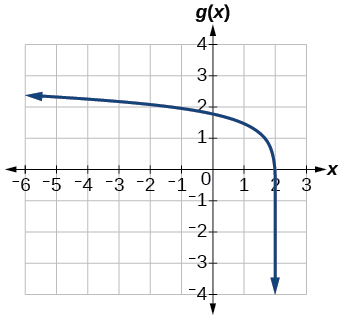
Answer: $Ex 4.4.43.png$

44) $h(x)=-\dfrac{1}{2}\log (x+1)-3$

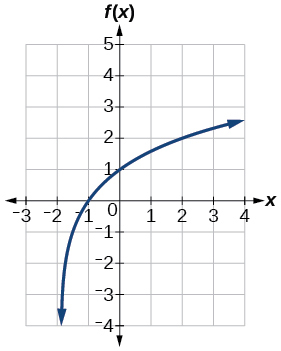
For the following exercises, write a logarithmic equation corresponding to the graph shown.

45) Use $y=\log _2(x)$as the parent function.

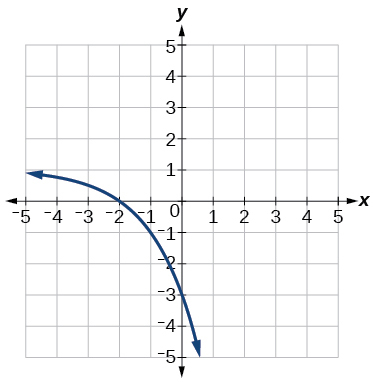
$CNX_PreCalc_Figure_04_02_214.jpg$

Answer: $f(x)=\log _2(-(x-1))$

46) Use $f(x)=\log _3(x)$ as the parent function.

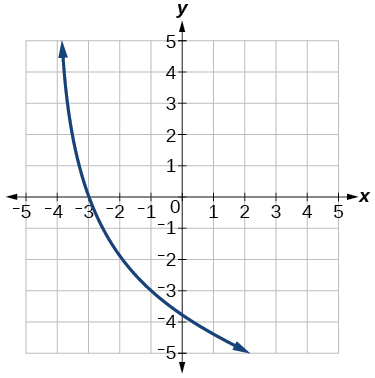
$CNX_PreCalc_Figure_04_04_215.jpg$

Exercise $\PageIndex{47}$

Use $f(x)=\log _4(x)$ as the parent function.

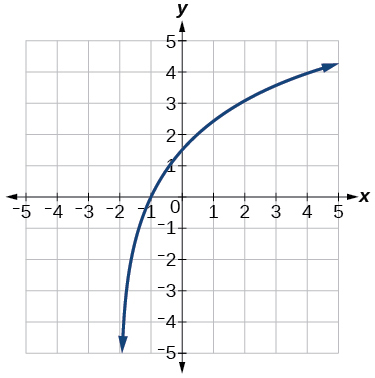
$CNX_PreCalc_Figure_04_04_216.jpg$

Answer: $f(x)=3\log _4(x+2)$

48) Use $f(x)=\log _5(x)$ as the parent function.

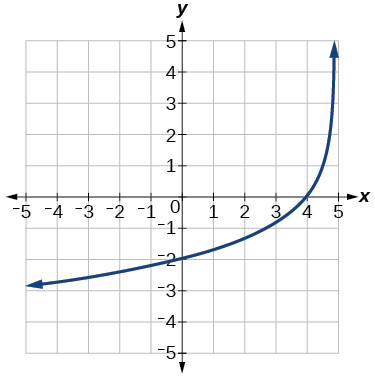
$CNX_PreCalc_Figure_04_04_217.jpg$

Technology

For the following exercises, use a graphing calculator to find approximate solutions to each equation.

49) $\log (x-1)+2=\ln (x-1)+2$

Answer: $x=2$

50) $\log (2x-3)+2=-\log (2x-3)+5$

51) $\ln (x-2)+2=-\ln (x+1)$

Answer: $x\approx 2.303$

52) $2\ln (5x+1)=\dfrac{1}{2}\ln (-5x)+1$

53) $\dfrac{1}{3}\log (1-x)=\log (x+1)+\dfrac{1}{3}$

Answer: $x\approx -0.472$

Extensions

54) Let $b$ be any positive real number such that $b\neq 1$What must $\log _b 1 $be equal to? Verify the result.

55) Explore and discuss the graphs of $f(x)=\log_{\frac{1}{2}}(x)$ and $g(x)=-\log _2(x)$Make a conjecture based on the result.

Answer

The graphs of $f(x)=\log_{\frac{1}{2}}(x)$ and $g(x)=-\log _2(x)$ appear to be the same;

Conjecture: for any positive base $b\neq 1$, $\log_{b}(x)=\log_{\frac{1}{b}}(x)$

56) Prove the conjecture made in the previous exercise.

57) What is the domain of the function $f(x)=\ln \left (\frac{x+2}{x-4} \right )$Discuss the result.

Answer

Recall that the argument of a logarithmic function must be positive, so we determine where $\frac{x+2}{x-4}> 0$. From the graph of the function $f(x)=\frac{x+2}{x-4}$ $,$ note that the graph lies above the $x$-axis on the interval $(-\infty ,-2)$ and again to the right of the vertical asymptote, that is $(4,\infty )$ Therefore, the domain is $(-\infty ,-2)\cup (4,\infty )$

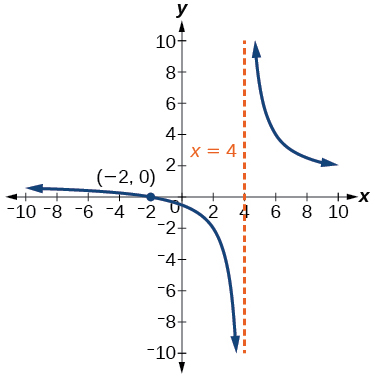
$CNX_Precalc_Figure_04_04_219.jpg$

58) Use properties of exponents to find the $x$-intercepts of the function $f(x)=\log \left ( x^2+4x+4 \right )$ algebraically. Show the steps for solving, and then verify the result by graphing the function.

Search

Text Color

Text Size

Margin Size

Font Type