2.8: Solve Absolute Value Inequalities
- Page ID
- 32415
Learning Objectives
By the end of this section, you will be able to:
- Solve absolute value equations
- Solve absolute value inequalities with “less than”
- Solve absolute value inequalities with “greater than”
- Solve applications with absolute value
Before you get started, take this readiness quiz.
- Evaluate: \(−|7|\).
If you missed this problem, review [link]. - Fill in \(<,>,<,>,\) or \(=\) for each of the following pairs of numbers.
ⓐ \(|−8|\text{___}−|−8|\) ⓑ \(12\text{___}−|−12|\) ⓒ \(|−6|\text{___}−6\) ⓓ \(−(−15)\text{___}−|−15|\)
If you missed this problem, review [link]. - Simplify: \(14−2|8−3(4−1)|\).
If you missed this problem, review [link].
Solve Absolute Value Equations
As we prepare to solve absolute value equations, we review our definition of absolute value.
ABSOLUTE VALUE
The absolute value of a number is its distance from zero on the number line.
The absolute value of a number n is written as \(|n|\) and \(|n|\geq 0\) for all numbers.
Absolute values are always greater than or equal to zero.
We learned that both a number and its opposite are the same distance from zero on the number line. Since they have the same distance from zero, they have the same absolute value. For example:
- \(−5\) is 5 units away from 0, so \(|−5|=5\).
- \(5\) is 5 units away from 0, so \(|5|=5\).
Figure \(\PageIndex{1}\) illustrates this idea.

For the equation |x|=5,|x|=5, we are looking for all numbers that make this a true statement. We are looking for the numbers whose distance from zero is 5. We just saw that both 5 and −5−5 are five units from zero on the number line. They are the solutions to the equation.
\(\begin{array} {ll} {\text{If}} &{|x|=5} \\ {\text{then}} &{x=−5\text{ or }x=5} \\ \end{array}\)
The solution can be simplified to a single statement by writing \(x=\pm 5\). This is read, “x is equal to positive or negative 5”.
We can generalize this to the following property for absolute value equations.
ABSOLUTE VALUE EQUATIONS
For any algebraic expression, u, and any positive real number, a,
\[\begin{array} {ll} {\text{if}} &{|u|=a} \\ {\text{then}} &{u=−a \text{ or }u=a} \\ \nonumber \end{array}\]
Remember that an absolute value cannot be a negative number.
Example \(\PageIndex{1}\)
Solve:
- \(|x|=8\)
- \(|y|=−6\)
- \(|z|=0\)
- Answer a
-
\(\begin{array} {ll} {} &{|x|=8} \\ {\text{Write the equivalent equations.}} &{x=−8 \text{ or } x=8} \\ {} &{x=\pn 8} \\ \end{array}\)
- Answer b
-
\(\begin{array} {ll} {} &{|y|=−6} \\ {} &{\text{No solution}} \\ \end{array}\)
Since an absolute value is always positive, there are no solutions to this equation. - Answer c
-
\(\begin{array} {ll} {} &{|z|=0} \\ {\text{Write the equivalent equations.}} &{z=−0\text{ or }z=0} \\ {\text{Since }−0=0,} &{z=0} \\ \end{array}\)
Both equations tell us that z=0z=0 and so there is only one solution.
Example \(\PageIndex{2}\)
Solve:
- \(|x|=2\)
- \(|y|=−4\)
- \(|z|=0\)
- Answer a
-
\(\pm 2\)
- Answer b
-
no solution
- Answer c
-
0
Example \(\PageIndex{3}\)
Solve:
- \(|x|=11\)
- \(|y|=−5\)
- \(|z|=0\)
- Answer a
-
\(\pm 11\)
- Answer b
-
no solution
- Answer c
-
0
To solve an absolute value equation, we first isolate the absolute value expression using the same procedures we used to solve linear equations. Once we isolate the absolute value expression we rewrite it as the two equivalent equations.
How to Solve Absolute Value Equations
Example \(\PageIndex{4}\)
Solve \(|5x−4|−3=8\).
- Answer
-




Example \(\PageIndex{5}\)
Solve: \(|3x−5|−1=6\).
- Answer
-
\(x=4, \space x=−\frac{2}{3}\)
Example \(\PageIndex{6}\)
Solve: \(|4x−3|−5=2\).
- Answer
-
\(x=−1,\space x=\frac{5}{2}\)
The steps for solving an absolute value equation are summarized here.
SOLVE ABSOLUTE VALUE EQUATIONS.
- Isolate the absolute value expression.
- Write the equivalent equations.
- Solve each equation.
- Check each solution.
Example \(\PageIndex{7}\)
Solve \(2|x−7|+5=9\).
- Answer
-
\(2|x−7|+5=9\) Isolate the absolute value expression. \(2|x−7|=4\) \(|x−7|=2\) Write the equivalent equations. \(x−7=−2\) or \(x−7=2\) Solve each equation. \(x=5\) or \(x=9\) Check:
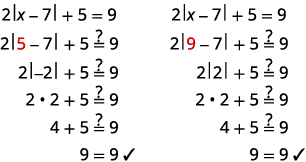
Example \(\PageIndex{8}\)
Solve: \(3|x−4|−4=8\).
- Answer
-
\(x=8,\space x=0\)
Example \(\PageIndex{9}\)
Solve: \(2|x−5|+3=9\).
- Answer
-
\(x=8,\space x=2\)
Remember, an absolute value is always positive!
Example \(\PageIndex{10}\)
Solve: \(|\frac{2}{3}x−4|+11=3\).
- Answer
-
\(\begin{array} {ll} {} &{|\frac{2}{3}x−4|=−8} \\ {\text{Isolate the absolute value term.}} &{|\frac{2}{3}x−4|=−8} \\ {\text{An absolute value cannot be negative.}} &{\text{No solution}} \\ \end{array}\)
Example \(\PageIndex{11}\)
Solve: \(|\frac{3}{4}x−5|+9=4\).
- Answer
-
No solution
Example \(\PageIndex{12}\)
Solve: \(|\frac{5}{6}x+3|+8=6\).
- Answer
-
No solution
Some of our absolute value equations could be of the form \(|u|=|v|\) where u and v are algebraic expressions. For example, \(|x−3|=|2x+1|\).
How would we solve them? If two algebraic expressions are equal in absolute value, then they are either equal to each other or negatives of each other. The property for absolute value equations says that for any algebraic expression, u, and a positive real number, a, if \(|u|=a\), then \(u=−a\) or \(u=a\).
This tell us that
\(\begin{array} {llllll} {\text{if}} &{|u|=|v|} &{} &{} &{} &{} \\ {\text{then]} &{u=−v} &{\text{or}} &{u=v} &{\text{or}} &{u=v} \\ \end{array}\)
This leads us to the following property for equations with two absolute values.
EQUATIONS WITH TWO ABSOLUTE VALUES
For any algebraic expressions, u and v,
\[\begin{array} {ll} {\text{if}} &{|u|=|v|} \\ {\text{then}} &{u=−v\text{ or }u=v} \\ \nonumber \end{array}\]
When we take the opposite of a quantity, we must be careful with the signs and to add parentheses where needed.
Example \(\PageIndex{13}\)
Solve: \(|5x−1|=|2x+3|\).
- Answer
-
\(\begin{array} {ll} {} &{} &{|5x−1|=|2x+3|} &{} \\ {} &{} &{} &{} \\ {\text{Write the equivalent equations.}} &{5x−1=−(2x+3)} &{\text{or}} &{5x−1=2x+3} \\ {} &{5x−1=−2x−3} &{\text{or}} &{3x−1=3} \\ {\text{Solve each equation.}} &{7x−1=−3} &{} &{3x=4} \\ {} &{7x=−2} &{} &{x=43} \\ {} &{x=−27} &{\text{or}} &{x=43} \\ {\text{Check.}} &{} &{} &{} \\ {\text{We leave the check to you.}} &{} &{} &{} \\ \end{array}\)
Example \(\PageIndex{14}\)
Solve: \(|7x−3|=|3x+7|\).
- Answer
-
\(x=−\frac{2}{5}, \space x=\frac{5}{2}\)
Example \(\PageIndex{15}\)
Solve: \(|6x−5|=|3x+4|\).
- Answer
-
\(x=3, x=19\)
Solve Absolute Value Inequalities with “Less Than”
Let’s look now at what happens when we have an absolute value inequality. Everything we’ve learned about solving inequalities still holds, but we must consider how the absolute value impacts our work. Again we will look at our definition of absolute value. The absolute value of a number is its distance from zero on the number line. For the equation \(|x|=5\), we saw that both 5 and \(−5\) are five units from zero on the number line. They are the solutions to the equation.
\[\begin{array} {lll} {} &{|x|=5} &{} \\ {x=−5} &{\text{or}} &{x=5} \\ \nonumber \end{array}\]
What about the inequality \(|x|\leq 5\)? Where are the numbers whose distance is less than or equal to 5? We know \(−5\) and 5 are both five units from zero. All the numbers between \(−5\) and 5 are less than five units from zero (Figure \(\PageIndex{2}\)).

In a more general way, we can see that if \(|u|\leq a\), then \(−a\leq u\leq a\) (Figure \(\PageIndex{3}\)).

This result is summarized here.
ABSOLUTE VALUE INEQUALITIES WITH \(<\) OR \(\leq\)
For any algebraic expression, u, and any positive real number, a,
\[ \text{if} \quad |u|<a, \quad \text{then} \space −a<u<a \\ \text{if} \quad |u|\leq a, \quad \text{then} \space−a\leq u\leq a \nonumber\]
After solving an inequality, it is often helpful to check some points to see if the solution makes sense. The graph of the solution divides the number line into three sections. Choose a value in each section and substitute it in the original inequality to see if it makes the inequality true or not. While this is not a complete check, it often helps verify the solution.
Example \(\PageIndex{16}\)
Solve \(|x|<7\). Graph the solution and write the solution in interval notation.
- Answer
-
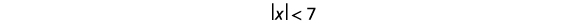
Write the equivalent inequality. 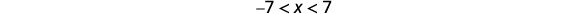
Graph the solution. 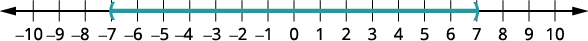
Write the solution using interval notation. 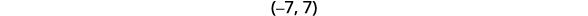
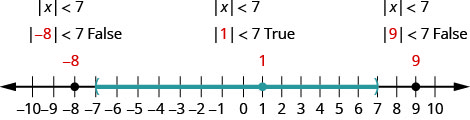
Check:
To verify, check a value in each section of the number line showing the solution. Choose numbers such as −8,−8, 1, and 9.
Example \(\PageIndex{17}\)
Graph the solution and write the solution in interval notation: \(|x|<9\).
- Answer
-
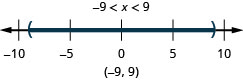
Example \(\PageIndex{18}\)
Graph the solution and write the solution in interval notation: \(|x|<1\).
- Answer
-
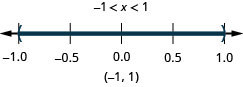
Example \(\PageIndex{19}\)
Solve \(|5x−6|\leq 4\). Graph the solution and write the solution in interval notation.
- Answer
-
Step 1. Isolate the absolute value expression.
It is isolated.\(|5x−6|\leq 4\) Step 2. Write the equivalent compound inequality. \(−4\leq 5x−6\leq 4\) Step 3. Solve the compound inequality. \(2\leq 5x\leq 10\)
\(\frac{2}{5}\leq x\leq 2\)Step 4. Graph the solution. 
Step 5. Write the solution using interval notation. \([\frac{2}{5}, 2]\) Check:
The check is left to you.
Example \(\PageIndex{20}\)
Solve \(|2x−1|\leq 5\). Graph the solution and write the solution in interval notation:
- Answer
-
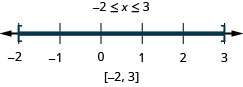
Example \(\PageIndex{21}\)
Solve \(|4x−5|\leq 3\). Graph the solution and write the solution in interval notation:
- Answer
-
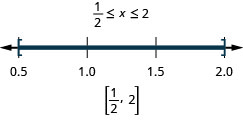
SOLVE ABSOLUTE VALUE INEQUALITIES WITH \(<\) OR \(\leq\)
- Isolate the absolute value expression.
- Write the equivalent compound inequality.
\[\begin{array} {lll} {|u|<a} &{\quad \text{is equivalent to}} &{−a<u<a} \\ {|u|\leq a} &{\quad \text{is equivalent to}} &{−a\leq u\leq a} \\ \nonumber \end{array}\]
- Solve the compound inequality.
- Graph the solution
- Write the solution using interval notation.
Solve Absolute Value Inequalities with “Greater Than”
What happens for absolute value inequalities that have “greater than”? Again we will look at our definition of absolute value. The absolute value of a number is its distance from zero on the number line.
We started with the inequality \(|x|\leq 5\). We saw that the numbers whose distance is less than or equal to five from zero on the number line were \(−5\) and 5 and all the numbers between \(−5\) and 5 (Figure \(\PageIndex{4}\)).

Now we want to look at the inequality \(|x|\geq 5\). Where are the numbers whose distance from zero is greater than or equal to five?
Again both \(−5\) and 5 are five units from zero and so are included in the solution. Numbers whose distance from zero is greater than five units would be less than \(−5\) and greater than 5 on the number line (Figure \(\PageIndex{5}\)).

In a more general way, we can see that if \(|u|\geq a\), then \(u\leq −a\) or \(u\leq a\). See Figure.

This result is summarized here.
ABSOLUTE VALUE INEQUALITIES WITH \(>\) OR \(\geq\)
For any algebraic expression, u, and any positive real number, a,
\[\begin{array} {lll} {\text{if}} &{\quad |u|>a,} &{\quad \text{then } u<−a \text{ or } u>a} \\ {\text{if}} &{\quad |u|\geq a,} &{\quad \text{then } u\leq −a \text{ or } u\geq a} \\ \nonumber \end{array}\]
Example \(\PageIndex{22}\)
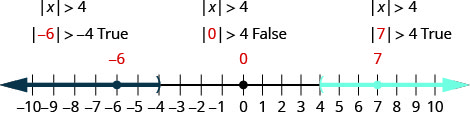
Solve \(|x|>4\). Graph the solution and write the solution in interval notation.
- Answer
-
\(|x|>4\) Write the equivalent inequality. \(x<−4\) or \(x>4\) Graph the solution. 
Write the solution using interval notation. \((−\inf ,−4)\cup (4,\inf )\) Check: To verify, check a value in each section of the number line showing the solution. Choose numbers such as −6,−6, 0, and 7.
Example \(\PageIndex{23}\)
Solve \(|x|>2\). Graph the solution and write the solution in interval notation.
- Answer
-
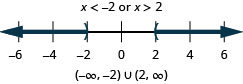
Example \(\PageIndex{24}\)
Solve \(|x|>1\). Graph the solution and write the solution in interval notation.
- Answer
-
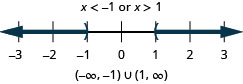
Example \(\PageIndex{25}\)
Solve \(|2x−3|\geq 5\). Graph the solution and write the solution in interval notation.
- Answer
-
\(|2x−3|\geq 5\) Step 1. Isolate the absolute value expression. It is isolated. Step 2. Write the equivalent compound inequality. \(2x−3\leq −5\) or \(2x−3\geq 5\) Step 3. Solve the compound inequality. \(2x\leq −2\) or \(2x\geq 8\)
\(x\leq −1\) or \(x\geq 4\)Step 4. Graph the solution. 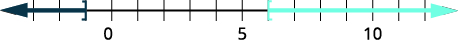
Step 5. Write the solution using interval notation. \((−\inf ,−1]\cup [4,\inf )\) Check:
The check is left to you.
Example \(\PageIndex{26}\)
Solve \(|4x−3|\geq 5\). Graph the solution and write the solution in interval notation.
- Answer
-
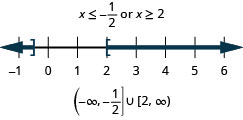
Example \(\PageIndex{27}\)
Solve \(|3x−4|\geq 2\). Graph the solution and write the solution in interval notation.
- Answer
-
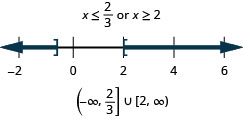
SOLVE ABSOLUTE VALUE INEQUALITIES WITH \(>\) OR \(\geq\).
- Isolate the absolute value expression.
- Write the equivalent compound inequality.
|u|>ais equivalent tou<−aoru>a|u|\geq ais equivalent tou\leq −aoru\geq a|u|>ais equivalent tou<−aoru>a|u|\geq ais equivalent tou\leq −aoru\geq a
- Solve the compound inequality.
- Graph the solution
- Write the solution using interval notation.
Solve Applications with Absolute Value
Absolute value inequalities are often used in the manufacturing process. An item must be made with near perfect specifications. Usually there is a certain tolerance of the difference from the specifications that is allowed. If the difference from the specifications exceeds the tolerance, the item is rejected.
\[|\text{actual-ideal}|\leq \text{tolerance} \nonumber\]
Example \(\PageIndex{28}\)
The ideal diameter of a rod needed for a machine is 60 mm. The actual diameter can vary from the ideal diameter by \(0.075\) mm. What range of diameters will be acceptable to the customer without causing the rod to be rejected?
- Answer
-
\(\begin{array} {ll} {} &{\text{Let }x=\text{ the actual measurement}} \\ {\text{Use an absolute value inequality to express this situation.}} &{|\text{actual-ideal}|\leq \text{tolerance}} \\ {} &{|x−60|\leq 0.075} \\ {\text{Rewrite as a compound inequality.}} &{−0.075\leq x−60\leq 0.075} \\ {\text{Solve the inequality.}} &{59.925\leq x\leq 60.075} \\ {\text{Answer the question.}} &{\text{The diameter of the rod can be between}} \\ {} &{59.925 mm \text{ and } 60.075 mm.} \\ \end{array}\)
Example \(\PageIndex{29}\)
The ideal diameter of a rod needed for a machine is 80 mm. The actual diameter can vary from the ideal diameter by 0.009 mm. What range of diameters will be acceptable to the customer without causing the rod to be rejected?
- Answer
-
The diameter of the rod can be between 79.991 and 80.009 mm.
Example \(\PageIndex{30}\)
The ideal diameter of a rod needed for a machine is 75 mm. The actual diameter can vary from the ideal diameter by 0.05 mm. What range of diameters will be acceptable to the customer without causing the rod to be rejected?
- Answer
-
The diameter of the rod can be between 74.95 and 75.05 mm.
Access this online resource for additional instruction and practice with solving linear absolute value equations and inequalities.
Key Concepts
- Absolute Value
The absolute value of a number is its distance from 0 on the number line.
The absolute value of a number n is written as \(|n|\) and \(|n|\geq 0\) for all numbers.
Absolute values are always greater than or equal to zero. - Absolute Value Equations
For any algebraic expression, u, and any positive real number, a,
\(\begin{array} {ll} {\text{if}} &{\quad |u|=a} \\ {\text{then}} &{\quad u=−a \text{ or } u=a} \\ \end{array}\)
Remember that an absolute value cannot be a negative number. - How to Solve Absolute Value Equations
- Isolate the absolute value expression.
- Write the equivalent equations.
- Solve each equation.
- Check each solution.
- Equations with Two Absolute Values
For any algebraic expressions, u and v,
\(\begin{array} {ll} {\text{if}} &{\quad |u|=|v|} \\ {\text{then}} &{\quad u=−v \text{ or } u=v} \\ \end{array}\) - Absolute Value Inequalities with \(<\) or \(\leq\)
For any algebraic expression, u, and any positive real number, a,
\(\begin{array} {llll} {\text{if}} &{\quad |u|=a} &{\quad \text{then}} &{−a<u<a} \\ {\text{if}} &{\quad |u|\leq a} &{\quad \text{then}} &{−a\leq u\leq a} \\ \end{array}\) - How To Solve Absolute Value Inequalities with \(<\) or \(\leq\)
- Isolate the absolute value expression.
- Write the equivalent compound inequality.
\(\begin{array} {lll} {|u|<a} &{\quad \text{is equivalent to}} &{\quad −a<u<a} \\ {|u|\leq a} &{\quad \text{is equivalent to}} &{\quad −a\leq u\leq a} \\ \end{array}\) - Solve the compound inequality.
- Graph the solution
- Write the solution using interval notation
- Absolute Value Inequalities with \(>\) or \(\geq\)
For any algebraic expression, u, and any positive real number, a,
\(\begin{array} {lll} {\text{if}} &{\quad |u|>a,} &{\text{then } u<−a\text{ or }u>a} \\ {\text{if}} &{\quad |u|\geq a,} &{\text{then } u\leq −a\text{ or }u\geq a} \\ \end{array}\) - How To Solve Absolute Value Inequalities with \(>\) or \(\geq\)
- Isolate the absolute value expression.
- Write the equivalent compound inequality.
\(\begin{array} {lll} {|u|>a} &{\quad \text{is equivalent to}} &{\quad u<−a\text{ or }u>a} \\ {|u|\geq a} &{\quad \text{is equivalent to}} &{\quad u\leq −a\text{ or }u\geq a} \\ \end{array}\) - Solve the compound inequality.
- Graph the solution
- Write the solution using interval notation

