9.3: “Seven Bridges of Konigsberg”

Through the city of Königsberg in Russia flowed the Pregel River. In this river were two large islands, which were part of the city. Joining the mainland either side of the river and those two islands there stood seven bridges.

Figure \(\PageIndex{1}\): Image is used under a CC-BY 3.0 license/Image by Leonhard Euler is in the public domain.

It was a popular exercise among the citizens to take a pleasure stroll across the bridges. The question naturally arose: was it possible to cross each bridge once and once only during the course of a single walk? More to the point: could this be done such that the walkers end up back at their starting point?

Solution

Leonhard Euler, a mathematician, solved the problem in 1735. This led to the beginning of graph theory and topology. Euler realized that the shape of the land and the positions of the bridges were irrelevant. What was important is the relationships between the land and the bridges. We can represent each of the landmasses as the vertices and the bridges as the edges of a multigraph:

Figure \(\PageIndex{2}\): Graph G: Konigsberg Bridges Graph. Image is used under a CC-BY 3.0 license.

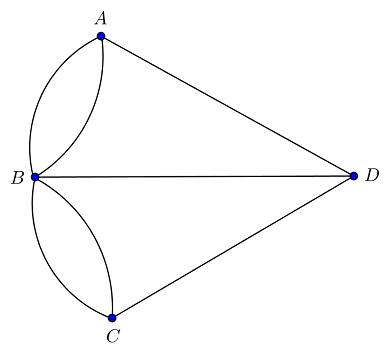
The question now evolves into: does this graph allow the construction of an Euler Path?

An Euler path is a trail T that passes through every edge of G exactly once. An Euler circuit is an Euler path that begins and ends at the same vertex (a loop).

Suppose you start at some vertex, say D, and end your trip at another, say A. Let’s say from D you sue the middle edge to reach B. You have to keep going, so you pick another edge from B to some other vertex. So, every time you enter B and leave B, you need two edges. When you come back to B, again you’ll have to leave B, so you need two more edges. In other words, B must have an even number of edges. In fact, every vertex needs an even number of edges, except at the starting point and the ending point.

In graph theory, the number of edges coming out of a vertex is called the “degree” (or “valence”) of the vertex and is denoted with “deg.” In this graph, deg (A)=3, deg (D)=3, deg (C)=3, and deg (B)=5. Remember, only the starting vertex and the ending vertex can have an odd degree. All other vertices are points to pass through, so they must have an even degree. Clearly, then, this graph G cannot have an Euler path.

In other words, one cannot take a stroll around Konigsberg crossing each bridge exactly once.

Now, if, in addition to crossing each bridge exactly once, you want to return to the starting vertex, then it is easy to see that EVERY vertex must have an even degree.

To summarize, here are the requirements so that an Euler path and an Euler circuit can exist for graph G:

1. G has an Euler path if exactly two vertices have an odd degree. An Euler path must begin and end at these two vertices.
2. G has an Euler circuit if and only if every vertex has an even degree.

Reference

1. References (23)

Contributors and Attributions

• Saburo Matsumoto
  CC-BY-4.0