3.1: Introduction to Systems of ODEs
- Last updated
- Save as PDF
- Page ID
- 32192
Often we do not have just one dependent variable and just one differential equation, we may end up with systems of several equations and several dependent variables even if we start with a single equation.
If we have several dependent variables, suppose \(y_1\), \(y_2\), ..., \(y_n\), then we can have a differential equation involving all of them and their derivatives. For example, \( y''_1= f(y'_1,y'_2,y_1,y_2,x)\). Usually, when we have two dependent variables we have two equations such as
\[\begin{align}\begin{aligned} y''_1&= f_1(y'_1,y'_2,y_1,y_2,x)\\ y''_2&= f_2(y'_1,y'_2,y_1,y_2,x)\end{aligned}\end{align} \nonumber \]
for some functions \(f_1\) and \(f_2\). We call the above a system of differential equations. More precisely, the above is a second order system of ODEs as second order derivatives appear. The system \[\begin{align}\begin{aligned} x_1' & = g_1(x_1,x_2,x_3,t) , \\ x_2' & = g_2(x_1,x_2,x_3,t) , \\ x_3' & = g_3(x_1,x_2,x_3,t) ,\end{aligned}\end{align} \nonumber \] is a first order system, where \(x_1,x_2,x_3\) are the dependent variables, and \(t\) is the independent variable.
The terminology for systems is essentially the same as for single equations. For the system above, a solution is a set of three functions \(x_1(t)\), \(x_2(t)\), \(x_3(t)\), such that \[\begin{align}\begin{aligned} x_1'(t) &= g_1\bigl(x_1(t),x_2(t),x_3(t),t\bigr) , \\ x_2'(t) &= g_2\bigl(x_1(t),x_2(t),x_3(t),t\bigr) , \\ x_3'(t) &= g_3\bigl(x_1(t),x_2(t),x_3(t),t\bigr) .\end{aligned}\end{align} \nonumber \]
We usually also have an initial condition. Just like for single equations we specify \(x_1\), \(x_2\), and \(x_3\) for some fixed \(t\). For example, \(x_1(0) = a_1\), \(x_2(0) = a_2\), \(x_3(0) = a_3\). For some constants \(a_1\), \(a_2\), and \(a_3\). For the second order system we would also specify the first derivatives at a point. And if we find a solution with constants in it, where by solving for the constants we find a solution for any initial condition, we call this solution the general solution. Best to look at a simple example.
Example \(\PageIndex{1}\)
Sometimes a system is easy to solve by solving for one variable and then for the second variable. Take the first order system
\[\begin{align} \begin{aligned} y'_1 &= y_1, \\ y'_2 &= y_1 - y_2,\end{aligned}\end{align} \nonumber \]
with initial conditions of the form \(y_1(0) = 1\) and \(y_2(0) = 2\).
Solution
We note that \( y_1 = C_1e^x\) is the general solution of the first equation. We then plug this \(y_1\) into the second equation and get the equation \(y'_2=C_1e^x-y_2\), which is a linear first order equation that is easily solved for \(y_2\). By the method of integrating factor we obtain
\[ e^xy_2 = \dfrac{C_1}{2}e^{2x} + C_2 \nonumber \] or \[ y_2 = \dfrac{C_1}{2}e^2 + C_2 e^{-x}. \nonumber \]
The general solution to the system is, therefore,
\[ y_1 = C_1e^e,\quad\text{and}\quad y_2 = \dfrac{C_1}{2}e^x + C_2e^{-x}. \nonumber \]
We now solve for \(C_1\) and \(C_2\) given the initial conditions. We substitute \(x=0\) and find that \(C_1 =1\) and \(C_2 =\frac{3}{2}\). Thus the solution is: \(y_1 = e^x,\) and \( y_2 = \dfrac{1}{2}e^x + \dfrac{3}{2}e^{-x}\).
Generally, we will not be so lucky to be able to solve for each variable separately as in the example above, and we will have to solve for all variables at once. While we won’t generally be able to solve for one variable and then the next, we will try to salvage as much as possible from this technique. It will turn out that in a certain sense we will still (try to) solve a bunch of single equations and put their solutions together. Let’s not worry right now about how to solve systems yet.
We will mostly consider the linear systems. The example above is a so-called linear first order system. It is linear as none of the dependent variables or their derivatives appear in nonlinear functions or with powers higher than one (\(x\), \(y\), \(x'\) and \(y'\), constants, and functions of \(t\) can appear, but not \(xy\) or \({(y')}^2\) or \(x^3\)). Another, more complicated, example of a linear system is \[\begin{align}\begin{aligned} y_1'' &= e^t y_1' + t^2 y_1 + 5 y_2 + \sin(t), \\ y_2'' &= t y_1'-y_2' + 2 y_1 + \cos(t).\end{aligned}\end{align} \nonumber \]
Applications
Let us consider some simple applications of systems and how to set up the equations.
Example \(\PageIndex{2}\)
First, we consider salt and brine tanks, but this time water flows from one to the other and back. We again consider that the tanks are evenly mixed.
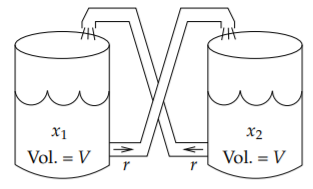
Suppose we have two tanks, each containing volume \(V\) liters of salt brine. The amount of salt in the first tank is \(x_1\) grams, and the amount of salt in the second tank is \(x_2\) grams. The liquid is perfectly mixed and flows at the rate \(r\) liters per second out of each tank into the other. See Figure \(\PageIndex{1}\).
The rate of change of \(x_1\), that is \(x_1'\), is the rate of salt coming in minus the rate going out. The rate coming in is the density of the salt in tank 2, that is \(\frac{x_2}{V}\), times the rate \(r\). The rate coming out is the density of the salt in tank 1, that is \(\frac{x_1}{V}\), times the rate \(r\). In other words it is \[x_1' = \frac{x_2}{V} r - \frac{x_1}{V} r = \frac{r}{V} x_2 - \frac{r}{V} x_1 = \frac{r}{V} (x_2-x_1). \nonumber \] Similarly we find the rate \(x_2'\), where the roles of \(x_1\) and \(x_2\) are reversed. All in all, the system of ODEs for this problem is \[\begin{align}\begin{aligned} x_1' & = \frac{r}{V} (x_2-x_1), \\ x_2' & = \frac{r}{V} (x_1-x_2).\end{aligned}\end{align} \nonumber \] In this system we cannot solve for \(x_1\) or \(x_2\) separately. We must solve for both \(x_1\) and \(x_2\) at once, which is intuitively clear since the amount of salt in one tank affects the amount in the other. We can’t know \(x_1\) before we know \(x_2\), and vice versa.
We don’t yet know how to find all the solutions, but intuitively we can at least find some solutions. Suppose we know that initially the tanks have the same amount of salt. That is, we have an initial condition such as \(x_1(0)=x_2(0) = C\). Then clearly the amount of salt coming and out of each tank is the same, so the amounts are not changing. In other words, \(x_1 = C\) and \(x_2 = C\) (the constant functions) is a solution: \(x_1' = x_2' = 0\), and \(x_2-x_1 = x_1-x_2 = 0\), so the equations are satisfied.
Let us think about the setup a little bit more without solving it. Suppose the initial conditions are \(x_1(0) = A\) and \(x_2(0) = B\), for two different constants \(A\) and \(B\). Since no salt is coming in or out of this closed system, the total amount of salt is constant. That is, \(x_1+x_2\) is constant, and so it equals \(A+B\). Intuitively if \(A\) is bigger than \(B\), then more salt will flow out of tank one than into it. Eventually, after a long time we would then expect the amount of salt in each tank to equalize. In other words, the solutions of both \(x_1\) and \(x_2\) should tend towards \(\frac{A+B}{2}\). Once you know how to solve systems you will find out that this really is so.
Example \(\PageIndex{3}\)
As an example application, let us think of mass and spring systems again.
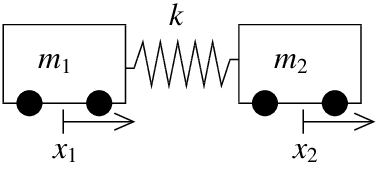
As an example application, let us think of mass and spring systems again. Suppose we have one spring with constant \(k\), but two masses \(m_1\) and \(m_2\). We can think of the masses as carts, and we will suppose that they ride along a straight track with no friction. Let \(x_1\) be the displacement of the first cart and \(x_2\) be the displacement of the second cart. That is, we put the two carts somewhere with no tension on the spring, and we mark the position of the first and second cart and call those the zero positions. Then \(x_1\) measures how far the first cart is from its zero position, and \(x_2\) measures how far the second cart is from its zero position. The force exerted by the spring on the first cart is \( k(x_2 - x_1)\), since \(x_2-x_1\) is how far the string is stretched (or compressed) from the rest position. The force exerted on the second cart is the opposite, thus the same thing with a negative sign.
Newton’s second law states that force equals mass times acceleration. So the system of equations governing the setup is
\[\begin{align}\begin{aligned} m_1x''_1 &= k(x_2 - x_1) \\ m_2x''_2&= -k(x_2 - x_1) \end{aligned}\end{align} \nonumber \]
In this system we cannot solve for the \(x_1\) or \(x_2\) variable separately. That we must solve for both \(x_1\) and \(x_2\) at once is intuitively clear, since where the first cart goes depends exactly on where the second cart goes and vice-versa.
Changing to First Order
Before we talk about how to handle systems, let us note that in some sense we need only consider first order systems. Let us take an \(n^{th}\) order differential equation
\[ y^{(n)} = F(y^{(n-1)}, ..., y', y, x ). \nonumber \]
We define new variables \(u_1, ..., u_n\) and write the system
\[\begin{align}\begin{aligned} u'_1 &= u_2 \\ u'_2 &= u_3 \\ &\vdots \\ u'_{n-1} &= u_n \\ u'_n &= F(u_n, u_{n-1}, \dots , u_2, u_1, x)\end{aligned}\end{align} \nonumber \]
We solve this system for \(u_1, u_2, \dots , u_n\). Once we have solved for the \(u\)’s, we can discard \(u_2\) through \(u_n\) and let \(y=u_1\). We note that this \(y\) solves the original equation.
Example \(\PageIndex{4}\)
Take \(x''' = 2x''+ 8x' + x + t\). Letting \(u_1 = x\), \(u_2 = x'\), \(u_3 = x''\), we find the system: \[u_1' = u_2, \qquad u_2' = u_3, \qquad u_3' = 2u_3 + 8u_2 + u_1 + t . \nonumber \]
A similar process can be followed for a system of higher order differential equations. For example, a system of \(k\) differential equations in \(k\) unknowns, all of order \(n\), can be transformed into a first order system of \(n \times k\) equations and \(n \times k\) unknowns.
Example \(\PageIndex{5}\)
Consider the system from the carts example, \[m_1 x_1'' = k(x_2-x_1), \qquad m_2 x_2'' = - k(x_2-x_1) . \nonumber \] Let \(u_1 = x_1\), \(u_2 = x_1'\), \(u_3 = x_2\), \(u_4 = x_2'\). The second order system becomes the first order system \[u_1' = u_2, \qquad m_1 u_2' = k(u_3-u_1), \qquad u_3' = u_4, \qquad m_2 u_4' = - k(u_3-u_1) . \nonumber \]
Example \(\PageIndex{6}\)
Sometimes we can use this idea in reverse as well. Let us take the system
\[ x' = 2y-x, \quad y'=x, \nonumber \]
where the independent variable is \(t\). We wish to solve for the initial conditions \(x(0)=1\) and \(y(0)=0\).
If we differentiate the second equation we get \(y''=x'\). We know what \(x'\) is in terms of \(x\) and \(y\), and we know that \(x=y'\).
\[ y''=x'=2y-x=2y-y'. \nonumber \]
We now have the equation \( y'' + y' - 2y = 0 \). We know how to solve this equation and we find that \( y = C_1e^{-2t} + C_2e^t \). Once we have \(y\) we use the equation \( y' = x\) to get \(x\).
\[ x = y' = -2C_1e^{-2t} + C_2e^t \nonumber \]
We solve for the initial conditions \( 1 = x(0) = -2C_1 + C_2 \) and \( 0 = y(0) = C_1 + C_2 \). Hence, \( C_1 = - C_2\) and \( 1 = 3C_2\). So \( C_1 = -\frac {1}{3} \) and \( C_2 = \frac {1}{3} \). Our solution is
\[ x = \frac {2e^{-2t} + e^t}{3}, \quad y = \frac {-e^{-2t} + e^t}{3} \nonumber \]
Exercise \(\PageIndex{1}\)
Plug in and confirm that this really is the solution.
It is useful to go back and forth between systems and higher order equations for other reasons. For example, software for solving ODE numerically (approximation) is generally for first order systems. To use it, you take whatever ODE you want to solve and convert it to a first order system. It is not very hard to adapt computer code for the Euler or Runge–Kutta method for first order equations to handle first order systems. We simply treat the dependent variable not as a number but as a vector. In many mathematical computer languages there is almost no distinction in syntax.
Autonomous Systems and Vector Fields
A system where the equations do not depend on the independent variable is called an autonomous system. For example the system \(x'=2y-x\), \(y'=x\) is autonomous as \(t\) is the independent variable but does not appear in the equations.
For autonomous systems we can draw the so-called direction field or vector field, a plot similar to a slope field, but instead of giving a slope at each point, we give a direction (and a magnitude). The previous example, \(x' = 2y-x\), \(y' = x\), says that at the point \((x,y)\) the direction in which we should travel to satisfy the equations should be the direction of the vector \(( 2y-x, x )\) with the speed equal to the magnitude of this vector. So we draw the vector \((2y-x,x)\) at the point \((x,y)\) and we do this for many points on the \(xy\)-plane. For example, at the point \((1,2)\) we draw the vector \(\bigl(2(2)-1,1\bigr) = (3,1)\), a vector pointing to the right and a little bit up, while at the point \((2,1)\) we draw the vector \(\bigl(2(1)-2,2\bigr) = (0,2)\) a vector that points straight up. When drawing the vectors, we will scale down their size to fit many of them on the same direction field. If we drew the arrows at the actual size, the diagram would be a jumbled mess once you would draw more than a couple of arrows. So we scale them all so that not even the longest one interferes with the others. We are mostly interested in their direction and relative size. See Figure \(\PageIndex{3}\).
We can draw a path of the solution in the plane. Suppose the solution is given by \(x = f(t)\), \(y=g(t)\). We pick an interval of \(t\) (say \(0 \leq t \leq 2\) for our example) and plot all the points \(\bigl(f(t),g(t)\bigr)\) for \(t\) in the selected range. The resulting picture is called the phase portrait (or phase plane portrait). The particular curve obtained is called the trajectory or solution curve. See an example plot in Figure \(\PageIndex{4}\). In the figure the solution starts at \((1,0)\) and travels along the vector field for a distance of 2 units of \(t\). We solved this system precisely, so we compute \(x(2)\) and \(y(2)\) to find \(x(2) \approx 2.475\) and \(y(2) \approx 2.457\). This point corresponds to the top right end of the plotted solution curve in the figure.
Notice the similarity to the diagrams we drew for autonomous systems in one dimension. But note how much more complicated things become when we allow just one extra dimension.
We can draw phase portraits and trajectories in the \(xy\)-plane even if the system is not autonomous. In this case, however, we cannot draw the direction field, since the field changes as \(t\) changes. For each \(t\) we would get a different direction field.


Picard’s theorem
Perhaps before going further, let us mention that Picard’s theorem on existence and uniqueness still holds for systems of ODE. Let us restate this theorem in the setting of systems. A general first order system is of the form \[ \begin{align} \begin{aligned} x_1' & = F_1(x_1,x_2,\ldots,x_n,t) , \\ x_2' & = F_2(x_1,x_2,\ldots,x_n,t) , \\ & \vdots \\ x_n' & = F_n(x_1,x_2,\ldots,x_n,t) . \end{aligned}\end{align} \label{eq:1} \]
Theorem \(\PageIndex{1}\)
Picard's Theorem on Existence and Uniqueness for Systems
If for every \(j=1,2,\ldots,n\) and every \(k = 1,2,\ldots,n\) each \(F_j\) is continuous and the derivative \(\frac{\partial F_j}{\partial x_k}\) exists and is continuous near some \((x_1^0,x_2^0,\ldots,x_n^0,t^0)\), then a solution to (3.1.21) subject to the initial condition \(x_1(t^0) = x_1^0\), \(x_2(t^0) = x_2^0\), …, \(x_n(t^0) = x_n^0\) exists (at least for \(t\) in some small interval) and is unique.
That is, a unique solution exists for any initial condition given that the system is reasonable (\(F_j\) and its partial derivatives in the \(x\) variables are continuous). As for single equations we may not have a solution for all time \(t\), but at least for some short period of time.
As we can change any \(n\)th order ODE into a first order system, then we notice that this theorem provides also the existence and uniqueness of solutions for higher order equations that we have until now not stated explicitly.


