6.4: Dirac delta and impulse response
- Last updated
- Save as PDF
- Page ID
- 32223
Rectangular Pulse
Often in applications we study a physical system by putting in a short pulse and then seeing what the system does. The resulting behavior is often called impulse response. Let us see what we mean by a pulse. The simplest kind of a pulse is a simple rectangular pulse defined by
\[ \varphi(t)= \left\{ \begin{array}{ccc} 0 & {\rm{if~}}~~~~t<a, \\ M & {\rm{if~}}a \leq t<b, \\ 0 & {\rm{if~}}b \leq t.\end{array} \right. \nonumber \]
Notice that \[\varphi (t) = M\left(u(t-a)-u(t-b)\right), \nonumber \] where \(u(t)\) is the unit step function (see Figure \(\PageIndex{1}\) for a graph).
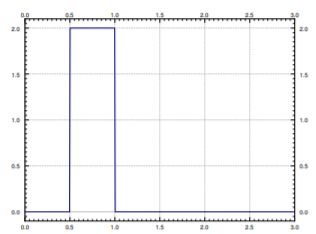
Let us take the Laplace transform of a square pulse,
\[\begin{align}\begin{aligned} \mathcal{L}\{ \varphi(t)\} &= \mathcal{L}\{ M(u(t-a)-u(t-b)) \} &= M \frac{e^{-as}-e^{-bs}}{s}.\end{aligned}\end{align} \nonumber \]
For simplicity we let \(a=0\) and it is convenient to set \(M= \dfrac{1}{b}\) to have
\[ \int _0 ^{\infty} \varphi (t) \; dt = 1 \nonumber \]
That is, to have the pulse have “unit mass.” For such a pulse we compute
\[ \mathcal{L}\{ \varphi(t)\}= \mathcal{L}\left\{ \frac{u(t)-u(t-b)}{b} \right\} = \frac{1-e^{-bs}}{bs}. \nonumber \]
We generally want \(b\) to be very small. That is, we wish to have the pulse be very short and very tall. By letting \(b\) go to zero we arrive at the concept of the Dirac delta function.
6.4.2Delta Function
The Dirac delta function\(^{1}\) is not exactly a function; it is sometimes called a generalized function. We avoid unnecessary details and simply say that it is an object that does not really make sense unless we integrate it. The motivation is that we would like a “function” \(\delta (t)\) such that for any continuous function \(f(t)\) we have
\[ \int_{-\infty}^{\infty} \delta (t) f(t) \, dt = f(0) \nonumber \]
The formula should hold if we integrate over any interval that contains 0, not just \((-\infty, \infty)\). So \(\delta (t)\) is a “function” with all its “mass” at the single point \(t=0\). In other words, for any interval \([c,d]\)
\[ \int_c^d \delta(t)= \left\{ \begin{array}{cl} 1 & {\rm{if~the~interval~}} [c,d]{\rm{~contains~}}0, {\rm{~i.e.~}}c \leq 0 \leq d, \\ 0 & {\rm{otherwise}}. \end{array} \right. \nonumber \]
Unfortunately there is no such function in the classical sense. You could informally think that \(\delta (t)\) is zero for \(t \neq 0\) and somehow infinite at \(t=0\).
A good way to think about \(\delta (t)\) is as a limit of short pulses whose integral is 1. For example, suppose that we have a square pulse \(\varphi (t)\) as above with \(a=0\), \(M=\dfrac{1}{b}\), that is \(\varphi (t) = \dfrac{u(t)-u(t-b)}{b} \).
Compute
\[ \int_{-\infty}^{\infty} \varphi (t) f(t) \, dt = \int_{-\infty}^{\infty} \dfrac{u(t)-u(t-b)}{b} f(t) \, dt =\dfrac{1}{b} \int_{0}^{b} f(t) \, dt. \nonumber \]
If \(f(t)\) is continuous at \(t=0\), then for very small \(b\), the function \(f(t)\) is approximately equal to \(f(0)\) on the interval \([0,b)\). We approximate the integral
\[ \dfrac{1}{b} \int_0^b f(t) \, dt \approx \dfrac{1}{b} \int_0^b f(t) \, dt = f(0). \nonumber \]
Therefore,
\[ \lim _{b \rightarrow 0} \int_{-\infty}^{\infty} \varphi (t) f(t) \, dt = \lim _{b \rightarrow 0} \dfrac{1}{b} \int_0^b f(t) \, dt = f(0) \nonumber \]
Let us therefore accept \(\delta (t)\) as an object that is possible to integrate. We often want to shift \(\delta\) to another point, for example \(\delta (t-a)\). In that case we have
\[ \int_{-\infty}^{\infty} \delta(t-a) f(t) \, dt = f(a). \nonumber \]
Note that \(\delta (a-t)\) is the same object as \(\delta (t-a)\). In other words, the convolution of \(\delta (t)\) with \(f(t)\) is again \(f(t)\),
\[ (f * \delta)(t) = \int _0^t \delta(t-s)f(s)\, ds = f(t) \nonumber \]
As we can integrate \(\delta (t)\), let us compute its Laplace transform.
\[ \mathcal{L} \{\delta (t-a) \} = \int_0^{\infty} e^{-st} \delta(t-a) \, dt = e^{-as}. \nonumber \]
In particular,
\[ \mathcal{L} \{\delta (t) \} = 1. \nonumber \]
Note
Notice that the Laplace transform of \(\delta (t-a)\) looks like the Laplace transform of the derivative of the Heaviside function \(u(t-a)\), if we could differentiate the Heaviside function. First notice
\[ \mathcal{L} \{\delta (t-a) \} = \dfrac{e^{-as}}{s}. \nonumber \]
To obtain what the Laplace transform of the derivative would be we multiply by \(s\), to obtain \(e^{-as}\), which is the Laplace transform of \(\delta (t-a)\). We see the same thing using integration,
\[ \int _0^{t} \delta (s-a) \,ds = u(t-a) \nonumber \]
So in a certain sense
\[ \dfrac{d}{dt} [u(t-a)] = \delta(t-a) \nonumber \]
This line of reasoning allows us to talk about derivatives of functions with jump discontinuities. We can think of the derivative of the Heaviside function \(u(t-a)\) as being somehow infinite at \(a\), which is precisely our intuitive understanding of the delta function.
Example \(\PageIndex{1}\)
Compute
\[ \mathcal{L}^{-1} \left\{ \dfrac{s+1}{s} \right\}. \nonumber \]
So far we have always looked at proper rational functions in the \(s\) variable. That is, the numerator was always of lower degree than the denominator. Not so with \(\dfrac{s+1}{s}\). We write,
\[ \mathcal{L}^{-1} \left\{ \dfrac{s+1}{s} \right\} = \mathcal{L}^{-1} \left\{ 1+ \dfrac{1}{s} \right\} = \mathcal{L}^{-1} \{1\} + \mathcal{L}^{-1} \left\{ \dfrac{1}{s} \right\} = \delta(t) + 1. \nonumber \]
The resulting object is a generalized function and only makes sense when put underneath an integral.
Impulse Response
As we said before, in the differential equation \( Lx = f(t)\), we think of \(f(t)\) as input, and \(x(t)\) as the output. Often it is important to find the response to an impulse, and then we use the delta function in place of \(f(t)\). The solution to
\[ Lx = \delta (t) \nonumber \]
is called the impulse response.
Example \(\PageIndex{2}\)
Solve (find the impulse response)
\[\label{eq:20} x'' + \omega_0^2x=\delta(t) ,\quad x(0)=0 ,\quad x'(0)=0. \]
We first apply the Laplace transform to the equation. Denote the transform of \(x(t)\) by \(X(s)\).
\[ s^2X(s) + \omega^2_0X(s) = 1,\quad\text{and so}\quad X(s) = \dfrac{1}{s^2+\omega^2_0}. \nonumber \]
Taking the inverse Laplace transform we obtain
\[x(t)=\frac{\sin (\omega_{0}t)}{\omega_{0}}. \nonumber \]
Let us notice something about the above example. In Example 6.3.4, we found that when the input was \(f(t)\), then the solution to \( Lx = f(t)\) was given by
\[ x(t) = \int_0^t f(\tau)\dfrac{\sin \left(\omega_0(t-\tau) \right)}{\omega_0} d\tau. \nonumber \]
Notice that the solution for an arbitrary input is given as convolution with the impulse response. Let us see why. The key is to notice that for functions \(x(t)\) and \(f(t)\),
\[ (x*f)''(t) = \dfrac{d^2}{dt^2} \left[ \int_0^t f(\tau)x(t-\tau)\,d\tau \right] = \int _0^t f(\tau)x''(t-\tau)\, d\tau = (x'' * f)(t). \nonumber \]
We simply differentiate twice under the integral,\(^{2}\) the details are left as an exercise. And so if we convolve the entire equation \(\eqref{eq:20}\), the left hand side becomes
\[ (x'' + \omega_0^2x)* f = (x'' * f) + \omega_0^2(x*f) = (x*f)'' + \omega_0^2(x*f). \nonumber \]
The right hand side becomes
\[ (\delta * f)(t) = f(t). \nonumber \]
Therefore \(y(t) = (x*f)(t)\) is the solution to
\[ y'' + \omega_0^2y = f(t). \nonumber \]
This procedure works in general for other linear equations \(Lx=f(t)\). If you determine the impulse response, you also know how to obtain the output \(x(t)\) for any input \(f(t)\) by simply convolving the impulse response and the input \(f(t)\).
Three-Point Beam Bending
Let us give another quite different example where the delta function turns up: Representing point loads on a steel beam. Consider a beam of length \(L\), resting on two simple supports at the ends. Let \(x\) denote the position on the beam, and let \(y(x)\) denote the deflection of the beam in the vertical direction. The deflection \(y(x)\) satisfies the Euler-Bernoulli equation,\(^{3}\) \[EI \frac{d^4 y}{dx^4} = F(x) , \nonumber \] where \(E\) and \(I\) are constants\(^{4}\) and \(F(x)\) is the force applied per unit length at position \(x\). The situation we are interested in is when the force is applied at a single point as in Figure \(\PageIndex{2}\).
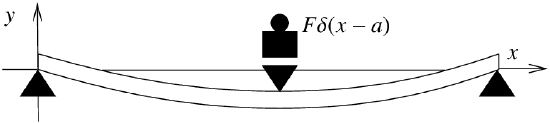
In this case the equation becomes
\[ EI\dfrac{d^4y}{dx^4}=-F\delta(x-a) \nonumber \]
where \(x=a\) is the point where the mass is applied. \(F\) is the force applied and the minus sign indicates that the force is downward, that is, in the negative \(y\) direction. The end points of the beam satisfy the conditions,
\[\begin{align}\begin{aligned} & y(0) = 0, \qquad y''(0) = 0, \\ & y(L) = 0, \qquad y''(L) = 0.\end{aligned}\end{align} \nonumber \]
See Section 5.2, for further information about endpoint conditions applied to beams.
Example \(\PageIndex{3}\)
Suppose that length of the beam is \(2\), and suppose that \(EI=1\) for simplicity. Further suppose that the force \(F=1\) is applied at \(x=1\). That is, we have the equation
\[ \dfrac{d^4y}{dx^4}=-\delta(x-1) \nonumber \]
and the endpoint conditions are
\[ y(0)=0,\quad y''(0)=0,\quad y(2)=0,\quad y''(2)=0. \nonumber \]
We could integrate, but using the Laplace transform is even easier. We apply the transform in the \(x\) variable rather than the \(t\) variable. Let us again denote the transform of \(y(x)\) as \(Y(s)\).
\[ s^4Y(s)-s^3y(0)-s^2y'(0)-sy''(0)-y'''(0)=-e^{-s}. \nonumber \]
We notice that \(y(0)=0\) and \(y''(0)=0\). Let us call \(C_1=y'(0)\) and \(C^2=y'''(0)\). We solve for \(Y(s)\),
\[ Y(s)=\frac{-e^{-s}}{s^4}+\frac{C_1}{s^2}+\frac{C_2}{s^4}. \nonumber \]
We take the inverse Laplace transform utilizing the second shifting property Equation (6.2.14) to take the inverse of the first term.
\[ y(x)=\frac{-(x-1)^3}{6}u(x-1)+C_1x+ \frac{C_2}{6}x^3. \nonumber \]
We still need to apply two of the endpoint conditions. As the conditions are at \(x=2\) we can simply replace \(u(x-1)=1\) when taking the derivatives. Therefore,
\[ 0=y(2)=\frac{-(2-1)^3}{6}+C_1(2)+ \frac{C_2}{6}2^3=\frac{-1}{6}+2C_1+\frac{4}{3C_2}, \nonumber \]
and
\[0 = y''(2) = \frac{-3\cdot 2 \cdot (2-1)}{6} + \frac{C_2}{6} 3\cdot 2 \cdot 2 = -1 + 2 C_2 \nonumber \]
Hence \(C_2 = \frac{1}{2}\) and solving for \(C_{1}\) using the first equation we obtain \(C_1 = \frac{-1}{4}\). Our solution for the beam deflection is \[y(x) = \frac{-{(x-1)}^3}{6} u(x-1) - \frac{x}{4} + \frac{x^3}{12}. \nonumber \]
Footnotes
[1] Named after the English physicist and mathematician Paul Adrien Maurice Dirac (1902–1984).
[2] You should really think of the integral going over \((-\infty , \infty )\) rather than over \([0,t]\) and simply assume that \(f(t)\) and \(x(t)\) are continuous and zero for negative .
[3] Named for the Swiss mathematicians Jacob Bernoulli (1654–1705), Daniel Bernoulli —nephew of Jacob— (1700–1782), and Leonhard Paul Euler (1707–1783).
[4] \(E\) is the elastic modulus and \(I\) is the second moment of area. Let us not worry about the details and simply think of these as some given constants.


