Skip to main content
Mathematics LibreTexts

8.7: Higher Roots

  1. Last updated
  2. Save as PDF
  • Page ID
    79525

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    Learning Objectives

    By the end of this section, you will be able to:

    • Simplify expressions with higher roots
    • Use the Product Property to simplify expressions with higher roots
    • Use the Quotient Property to simplify expressions with higher roots
    • Add and subtract higher roots
    Note
    1. Simplify: \(y^{5}y^{4}\).
      If you missed this problem, review Example 6.2.7.
    2. Simplify: \((n^2)^6\).
      If you missed this problem, review Example 6.2.19.
    3. Simplify: \(\frac{x^8}{x^3}\).
      If you missed this problem, review Example 6.5.1.

    Simplify Expressions with Higher Roots

    Up to now, in this chapter we have worked with squares and square roots. We will now extend our work to include higher powers and higher roots.

    Let’s review some vocabulary first.

    \[\begin{array}{cc} {}&{}\\ {\textbf{We write:}}&{\textbf{We say:}}\\ {n^2}&{\text{n squared}}\\ {n^3}&{\text{n cubed}}\\ {n^4}&{\text{n to the fourth}}\\ {n^5}&{\text{n to the fifth}}\\ \nonumber \end{array}\]

    The terms ‘squared’ and ‘cubed’ come from the formulas for area of a square and volume of a cube.

    It will be helpful to have a table of the powers of the integers from −5to5. See Figure \(\PageIdnex{1}\).

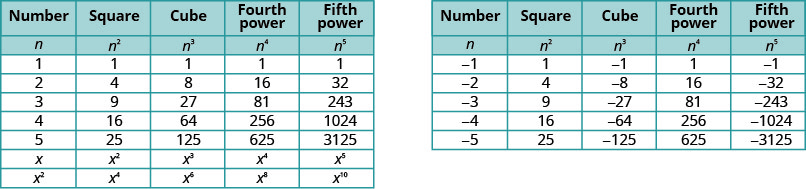
    This figure consists of two tables. The first table shows the results of raising the numbers 1, 2, 3, 4, 5, x, and x squared to the second, third, fourth, and fifth powers. The second table shows the results of raising the numbers negative one through negative five to the second, third, fourth, and fifth powers. The table first has five columns and nine rows. The second has five columns and seven rows. The columns in both tables are labeled, “Number,” “Square,” “Cube,” “Fourth power,” “Fifth power,” nothing, “Number,” “Square,” “Cube,” “Fourth power,” and “Fifth power.” In both tables, the next row reads: n, n squared, n cubed, n to the fourth power, n to the fifth power, nothing, n, n squared, n cubed, n to the fourth power, and n to the fifth power. In the first table, 1 squared, 1 cubed, 1 to the fourth power, and 1 to the fifth power are all shown to be 1. In the next row, 2 squared is 4, 2 cubed is 8, 2 to the fourth power is 16, and 2 to the fifth power is 32. In the next row, 3 squared is 9, 3 cubed is 27, 3 to the fourth power is 81, and 3 to the fifth power is 243. In the next row, 4 squared is 16, 4 cubed is 64, 4 to the fourth power is 246, and 4 to the fifth power is 1024. In the next row, 5 squared is 25, 5 cubed is 125, 5 to the fourth power is 625, and 5 to the fifth power is 3125. In the next row, x squared, x cubed, x to the fourth power, and x to the fifth power are listed. In the next row, x squared squared is x to the fourth power, x cubed squared is x to the fifth power, x squared to the fourth power is x to the eighth power, and x squared to the fifth power is x to the tenth power. In the second table, negative 1 squared is 1, negative 1 cubed is negative 1, negative 1 to the fourth power is 1, and negative 1 to the fifth power is negative 1. In the next row, negative 2 squared is 4, negative 2 cubed is negative 8, negative 2 to the fourth power is 16, and negative 2 to the fifth power is negative 32. In the next row, negative 4 squared is 16, negative 4 cubed is negative 64, negative 4 to the fourth power is 256, and negative 4 to the fifth power is negative 1024. In the next row, negative 5 squared is 25, negative 5 cubed is negative 125, negative 5 to the fourth power is 625, and negative 5 to the fifth power is negative 3125.
    Figure \(\PageIndex{1}\): First through fifth powers of integers from −5 to 5.

    Notice the signs in Figure \(\PageIndex{1}\). All powers of positive numbers are positive, of course. But when we have a negative number, the even powers are positive and the odd powers are negative. We’ll copy the row with the powers of −2 below to help you see this.

    This figure has five columns and two rows. The first row labels each column: n, n squared, n cubed, n to the fourth power, and n to the fifth power. The second row reads: negative 2, 4, negative 8, 16, and negative 32.

    Earlier in this chapter we defined the square root of a number.

    If \(n^2=m\),then n is a square root of m.

    And we have used the notation \(\sqrt{m}\) to denote the principal square root. So \(\sqrt{m} \ge 0\) always.

    We will now extend the definition to higher roots.

    Definition: NTH ROOT OF A NUMBER

    If \(b^n=a\), then b is an nth root of a number a.

    The principal nth root of a is written \(\sqrt[n]{a}=b\)

    n is called the index of the radical.

    We do not write the index for a square root. Just like we use the word ‘cubed’ for \(b^3\), we use the term ‘cube root’ for \(\sqrt[3]{a}\).

    We refer to Figure \(\PageIndex{1}\) to help us find higher roots.

    \[\begin{array}{cc} {4^3=64}&{\sqrt[3]{64}=4}\\ {3^4=81}&{\sqrt[4]{81}=3}\\ {(−2)^5=−32}&{\sqrt[5]{−32}=−2}\\ \nonumber \end{array}\]

    Could we have an even root of a negative number? No. We know that the square root of a negative number is not a real number. The same is true for any even root. Even roots of negative numbers are not real numbers. Odd roots of negative numbers are real numbers.

    Definition: PROPERTIES OF \(\sqrt[n]{a}\)

    When n is an even number and

    • \(a\ge 0\), then \(\sqrt[n]{a}\) is a real number
    • \(a < 0\), then \(\sqrt[n]{a}\) is not a real number

    When n is an odd number, \(\sqrt[n]{a}\) is a real number for all values of a.

    Example \(\PageIndex{1}\)

    Simplify:

    1. \(\sqrt[3]{8}\)
    2. \(\sqrt[4]{81}\)
    3. \(\sqrt[5]{32}\).
    Answer
    1. \(\sqrt[3]{8}\)
    Since \((2)^3=8\). 2
    2. \(\sqrt[4]{81}\)
    Since \((3)^4=81\). 3
    3. \(\sqrt[5]{32}\)
    Since \((2)^5=32\). 2
    Example \(\PageIndex{2}\)

    Simplify:

    1. \(\sqrt[3]{27}\)
    2. \(\sqrt[4]{256}\)
    3. \(\sqrt[5]{243}\).
    Answer
    1. 3
    2. 4
    3. 3
    Example \(\PageIndex{3}\)

    Simplify:

    1. \(\sqrt[3]{1000}\)
    2. \(\sqrt[4]{16}\)
    3. \(\sqrt[5]{32}\).
    Answer
    1. 10
    2. 2
    3. 2
    Example \(\PageIndex{4}\)

    Simplify:

    1. \(\sqrt[3]{−64}\)
    2. \(\sqrt[4]{−16}\)
    3. \(\sqrt[5]{−243}\).
    Answer
    1. \(\sqrt[3]{−64}\)
    Since \((−4)^3=−64\). −4
    2. \(\sqrt[4]{−16}\)
    Think, \((?)^4=−16\).No real number raised to the fourth power is positive. Not a real number.
    3. \(\sqrt[5]{−243}\)
    Since \((−3)^5=−243\). −3
    Example \(\PageIndex{5}\)

    Simplify:

    1. \(\sqrt[3]{−125}\)
    2. \(\sqrt[4]{−16}\)
    3. \(\sqrt[5]{−32}\).
    Answer
    1. −5
    2. not real
    3. −2
    Example \(\PageIndex{6}\)

    Simplify:

    1. \(\sqrt[3]{−216}\)
    2. \(\sqrt[4]{−81}\)
    3. \(\sqrt[5]{−1024}\).
    Answer
    1. −6
    2. not real
    3. −4
    When we worked with square roots that had variables in the radicand, we restricted the variables to non-negative values. Now we will remove this restriction.

    The odd root of a number can be either positive or negative. We have seen that \(\sqrt[3]{−64}=−4\).

    But the even root of a non-negative number is always non-negative, because we take the principal nth root.

    Suppose we start with a=−5.

    \[\begin{array}{cc} {(−5)^4=625}&{\sqrt[4]{625}=5}\\ \nonumber \end{array}\]

    How can we make sure the fourth root of −5 raised to the fourth power, \((−5)^4\) is 5? We will see in the following property.

    Definition: SIMPLIFYING ODD AND EVEN ROOTS

    For any integer \(n \ge 2\),

    \[\begin{array}{cc} {\text{when n is odd}}&{\sqrt[n]{a^n}=a}\\ {\text{when n is even}}&{\sqrt[n]{a^n}=|a|}\\ \nonumber \end{array}\]

    We must use the absolute value signs when we take an even root of an expression with a variable in the radical.

    Example \(\PageIndex{7}\)

    Simplify:

    1. \(\sqrt{x^2}\)
    2. \(\sqrt[3]{n^3}\)
    3. \(\sqrt[4]{p^4}\)
    4. \(\sqrt[5]{y^5}\).
    Answer

    We use the absolute value to be sure to get the positive root.

    1. \(\sqrt{x^2}\)
    Since \((x)^2=x^2\) and we want the positive root. |x|
    2. \(\sqrt[3]{n^3}\)
    Since \((n)^3=n^3\). It is an odd root so there is no need for an absolute value sign. n
    3. \(\sqrt[4]{p^4}\)
    Since \((p)^4=p^4\) and we want the positive root. |p|
    4. \(\sqrt[5]{y^5}\)
    Since \((y)^5=y^5\). It is an odd root so there is no need for an absolute value sign. y
    Example \(\PageIndex{8}\)

    Simplify:

    1. \(\sqrt{b^2}\)
    2. \(\sqrt[3]{w^3}\)
    3. \(\sqrt[4]{m^4}\)
    4. \(\sqrt[5]{q^5}\).
    Answer
    1. |b|
    2. w
    3. |m|
    4. q
    Example \(\PageIndex{9}\)

    Simplify:

    1. \(\sqrt{y^2}\)
    2. \(\sqrt[3]{p^3}\)
    3. \(\sqrt[4]{z^4}\)
    4. \(\sqrt[5]{q^5}\)
    Answer
    1. |y|
    2. p
    3. |z|
    4. q
    Example \(\PageIndex{10}\)

    Simplify:

    1. \(\sqrt[3]{y^{18}}\)
    2. \(\sqrt[4]{z^8}\).
    Answer
    1. \(\sqrt[3]{y^{18}}\)
    Since \((y^6)^3=y^18\). \(\sqrt[3]{(y^6)^3}\)
      \(y^6\)
    2. \(\sqrt[4]{z^8}\)
    Since \((z^2)^4=z^8\). \(\sqrt[4]{(z^2)^4}\)
    Since \(z^2\) is positive, we do not need an absolute value sign. \(z^2\)
    Example \(\PageIndex{11}\)

    Simplify:

    1. \(\sqrt[4]{u^{12}}\)
    2. \(\sqrt[3]{v^{15}}\).
    Answer
    1. \(u^3\)
    2. \(v^5\)
    Example \(\PageIndex{12}\)

    Simplify:

    1. \(\sqrt[5]{c^{20}}\)
    2. \(\sqrt[6]{d^{24}}\).
    Answer
    1. \(c^4\)
    2. \(d^4\)
    Example \(\PageIndex{13}\)

    Simplify:

    1. \(\sqrt[3]{64p^6}\)
    2. \(\sqrt[4]{16q^{12}}\).
    Answer
    1. \(\sqrt[3]{64p^6}\)
    Rewrite \(64p^6\) as \((4p^2)^3\). \(\sqrt[3]{(4p^2)^3}\)
    Take the cube root. \(4p^2\)
    2. \(\sqrt[4]{16q^{12}}\)
    Rewrite the radicand as a fourth power. \(\sqrt[4]{(2q^3)^4}\)
    Take the fourth root. \(2|q^3|\)
    Example \(\PageIndex{14}\)

    Simplify:

    1. \(\sqrt[3]{27x^{27}}\)
    2. \(\sqrt[4]{81q^{28}}\).
    Answer
    1. \(3x^9\)
    2. \(3∣q^7∣\)
    Example \(\PageIndex{15}\)

    Simplify:

    1. \(\sqrt[3]{125p^9}\)
    2. \(\sqrt[5]{243q^{25}}\)
    Answer
    1. \(5p^3\)
    2. \(3q^5\)

    Use the Product Property to Simplify Expressions with Higher Roots

    We will simplify expressions with higher roots in much the same way as we simplified expressions with square roots. An nth root is considered simplified if it has no factors of \(m^n\).

    Definition: SIMPLIFIED NTH ROOT

    \(\sqrt[n]{a}\) is considered simplified if a has no factors of \(m^n\).

    We will generalize the Product Property of Square Roots to include any integer root \(n \ge 2\).

    Definition: PRODUCT PROPERTY OF NTH ROOTs

    \(\sqrt[n]{ab}=\sqrt[n]{a}·\sqrt[n]{b}\) and \(\sqrt[n]{a}·\sqrt[n]{b}=\sqrt[n]{ab}\)

    when \(\sqrt[n]{a}\) and \(\sqrt[n]{b}\) are real numbers and for any integer \(n \ge 2\)

    Example \(\PageIndex{16}\)

    Simplify:

    1. \(\sqrt[3]{x^4}\)
    2. \(\sqrt[4]{x^7}\).
    Answer

    1.

    		 \(\sqrt[3]{x^4}\)
    Rewrite the radicand as a product using the largest perfect cube factor. \(\sqrt[3]{x^3·x}\)
    Rewrite the radical as the product of two radicals. \(\sqrt[3]{x^3}·\sqrt[3]{x}\)
    Simplify. \(x\sqrt[3]{x}\)
    2. \(\sqrt[4]{x^7}\)
    Rewrite the radicand as a product using the greatest perfect fourth power factor. \(\sqrt[4]{x^4·x^3}\)
    Rewrite the radical as the product of two radicals. \(\sqrt[4]{x^4}·\sqrt[4]{x^3}\)
    Simplify. \(|x|\sqrt[4]{x^3}\)
    Example \(\PageIndex{17}\)

    Simplify:

    1. \(\sqrt[4]{y^6}\)
    2. \(\sqrt[3]{z^5}\).
    Answer
    1. \(|y∣\sqrt[4]{y^2}\)
    2. \(z\sqrt[3]{z^2}\)
    Example \(\PageIndex{18}\)

    Simplify:

    1. \(\sqrt[5]{p^8}\)
    2. \(\sqrt[6]{q^{13}}\).
    Answer
    1. \(p\sqrt[5]{p^3}\)
    2. \( q^2\sqrt[6]{q}\)
    Example \(\PageIndex{19}\)

    Simplify:

    1. \(\sqrt[3]{16}\)
    2. \(\sqrt[4]{243}\).
    Answer
    1. \(\sqrt[3]{16}\)
      \(\sqrt[3]{2^4}\)
    Rewrite the radicand as a product using the largest perfect cube factor. \(\sqrt[3]{2^3·2}\)
    Rewrite the radical as the product of two radicals. \(\sqrt[3]{2^3}·\sqrt[3]{2}\)
    Simplify. \(2\sqrt[3]{2}\)
    2. \(\sqrt[4]{243}\)
      \(\sqrt[4]{3^5}\)
    Rewrite the radicand as a product using the greatest perfect fourth power factor. \(\sqrt[4]{3^4·3}\)
    Rewrite the radical as the product of two radicals. \(\sqrt[4]{3^4}·\sqrt[4]{3}\)
    Simplify. \(3\sqrt[4]{3}\)
    Example \(\PageIndex{20}\)

    Simplify:

    1. \(\sqrt[3]{81}\)
    2. \(\sqrt[4]{64}\).
    Answer
    1. \(3\sqrt[3]{3}\)
    2. \(2\sqrt[4]{4}\)
    Example \(\PageIndex{21}\)

    Simplify:

    1. \(\sqrt[3]{625}\)
    2. \(\sqrt[4]{729}\).
    Answer
    1. \(5\sqrt[3]{5}\)
    2. \(3\sqrt[4]{9}\)

    Don’t forget to use the absolute value signs when taking an even root of an expression with a variable in the radical.

    Example \(\PageIndex{22}\)

    Simplify:

    1. \(\sqrt[3]{24x^7}\)
    2. \(\sqrt[4]{80y^{14}}\).
    Answer
    1. \(\sqrt[3]{24x^7}\)
    Rewrite the radicand as a product using perfect cube factors. \(\sqrt[3]{2^{3}x^{6}·3x}\)
    Rewrite the radical as the product of two radicals. \(\sqrt[3]{2^{3}x^{6}}·\sqrt[3]{3x}\)
    Rewrite the first radicand as \((2x^2)^3\) \(\sqrt[3]{(2x^{2})^3}·\sqrt[3]{3x}\)
    Simplify. \(2x^2\sqrt[3]{3x}\)
    2. \(\sqrt[4]{80y^{14}}\)
    Rewrite the radicand as a product using perfect fourth power factors. \(\sqrt[4]{2^{4}y^{12}·5y^2}\)
    Rewrite the radical as the product of two radicals. \(\sqrt[4]{2^{4}y^{12}}·\sqrt[4]{5y^2}\)
    Rewrite the first radicand as \((2y^3)^4\) \(\sqrt[4]{(2y^3)^4}·\sqrt[4]{5y^2}\)
    Simplify. \(2|y^3|\sqrt[4]{5y^2}\)
    Example \(\PageIndex{23}\)

    Simplify:

    1. \(\sqrt[3]{54p^[10}]\)
    2. \(\sqrt[4]{64q^{10}}\).
    Answer
    1. \(3p^3\sqrt[3]{2p}\)
    2. \(2q^2\sqrt[4]{4q^2}\)
    Example \(\PageIndex{24}\)

    Simplify:

    1. \(\sqrt[3]{128m^{11}}\)
    2. \(\sqrt[4]{162n^7}\).
    Answer
    1. \(4m^3\sqrt[3]{2m^2}\)
    2. \(3|n|\sqrt[4]{2n^3}\)
    Example \(\PageIndex{25}\)

    Simplify:

    1. \(\sqrt[3]{−27}\)
    2. \(\sqrt[4]{−16}\).
    Answer
    1. \(\sqrt[3]{−27}\)
    Rewrite the radicand as a product using perfect cube factors. \(\sqrt[3]{(−3)^3}\)
    Take the cube root. −3
    2. \(\sqrt[4]{−16}\)
    There is no real number n where \(n^4=−16\). Not a real number.
    Example \(\PageIndex{26}\)

    Simplify:

    1. \(\sqrt[3]{−108}\)
    2. \(\sqrt[4]{−48}\).
    Answer
    1. \(−3\sqrt[3]{4}\)
    2. not real
    Example \(\PageIndex{27}\)

    Simplify:

    1. \(\sqrt[3]{−625}\)
    2. \(\sqrt[4]{−324}\).
    Answer
    1. \(−5\sqrt[3]{5}\)
    2. not real

    Use the Quotient Property to Simplify Expressions with Higher Roots

    We can simplify higher roots with quotients in the same way we simplified square roots. First we simplify any fractions inside the radical.

    Example \(\PageIndex{28}\)

    Simplify:

    1. \(\sqrt[3]{\frac{a^8}{a^5}}\)
    2. \(\sqrt[4]{\frac{a^{10}}{a^2}}\).
    Answer

    1.

    		 \(\sqrt[3]{\frac{a^8}{a^5}}\)
    Simplify the fraction under the radical first. \(\sqrt[3]{a^3}\)
    Simplify. a
    2. \(\sqrt[4]{\frac{a^{10}}{a^2}}\)
    Simplify the fraction under the radical first. \(\sqrt[4]{a^8}\)
    Rewrite the radicand using perfect fourth power factors. \(\sqrt[4]{(a^2)^4}\)
    Simplify. \(a^2\)
    Example \(\PageIndex{29}\)

    Simplify:

    1. \(\sqrt[4]{\frac{x^7}{x^3}}\)
    2. \(\sqrt[4]{\frac{y^{17}}{y^5}}\).
    Answer
    1. |x|
    2. \(y^3\)
    Example \(\PageIndex{30}\)

    Simplify:

    1. \(\sqrt[3]{\frac{m^{13}}{m^7}}\)
    2. \(\sqrt[5]{\frac{n^{12}}{n^2}}\).
    Answer
    1. \(m^2\)
    2. \(n^2\)

    Previously, we used the Quotient Property ‘in reverse’ to simplify square roots. Now we will generalize the formula to include higher roots.

    Definition: QUOTIENT PROPERTY OF NTH ROOTS

    \(\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\) and \(\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}\)

    when \(\sqrt[n]{a}\) and \(\sqrt[n]{b}\) are real numbers, \(b \ne 0\), and for any integer \(n \ge 2\)

    Exercise \(\PageIndex{31}\)

    Simplify:

    1. \(\frac{\sqrt[3]{−108}}{\sqrt[3]{2}}\)
    2. \(\frac{\sqrt[4]{96x^7}}{\sqrt[4]{3x^2}}\)
    Answer
    1. \(\frac{\sqrt[3]{−108}}{\sqrt[3]{2}}\)
    Neither radicand is a perfect cube, so use the Quotient Property to write as one radical. \(\sqrt[3]{\frac{−108}{2}}\)
    Simplify the fraction under the radical. \(\sqrt[3]{−54}\)
    Rewrite the radicand as a product using perfect cube factors. \(\sqrt[3]{(−3)^3·2}\)
    Rewrite the radical as the product of two radicals. \(\sqrt[3]{(−3)^3}·\sqrt[3]{2}\)
    Simplify. \(−3\sqrt[3]{2}\)
    2. \(\frac{\sqrt[4]{96x^7}}{\sqrt[4]{3x^2}}\)
    Neither radicand is a perfect fourth power, so use the Quotient Property to write as one radical \(\sqrt[4]{\frac{96x^7}{3x^2}}\)
    Simplify the fraction under the radical. \(\sqrt[4]{32x^5}\)
    Rewrite the radicand as a product using perfect fourth power factors. \(\sqrt[4]{2^{4}x^4·2x}\)
    Rewrite the radical as the product of two radicals. \(\sqrt[4]{(2x)^4}·\sqrt[4]{2x}\)
    Simplify. \(2|x|\sqrt[4]{2x}\)
    Example \(\PageIndex{32}\)

    Simplify:

    1. \(\frac{\sqrt[3]{−532}}{\sqrt[3]{2}}\)
    2. \(\frac{\sqrt[4]{486m^{11}}}{\sqrt[4]{3m^5}}\)
    Answer
    1. not real
    2. \(3|m|\sqrt[4]{2m^2}\)
    Example \(\PageIndex{33}\)

    Simplify:

    1. \(\frac{\sqrt[3]{−192}}{\sqrt[3]{3}}\)
    2. \(\frac{\sqrt[4]{324n^7}}{\sqrt[4]{2n^3}}\).
    Answer
    1. −4
    2. \(3|n|\sqrt[4]{2}\)

    If the fraction inside the radical cannot be simplified, we use the first form of the Quotient Property to rewrite the expression as the quotient of two radicals.

    Example \(\PageIndex{34}\)

    Simplify:

    1. \(\sqrt[3]{\frac{24x^7}{y^3}}\)
    2. \(\sqrt[4]{\frac{48x^{10}}{y^8}}\).
    Answer
    1. \(\sqrt[3]{\frac{24x^7}{y^3}}\)
    The fraction in the radicand cannot be simplified. Use the Quotient Property to write as two radicals. \(\frac{\sqrt[3]{24x^7}}{\sqrt[3]{y^3}}\)
    Rewrite each radicand as a product using perfect cube factors. \(\frac{\sqrt[3]{8x^6·3x}}{\sqrt[3]{y^3}}\)
    Rewrite the numerator as the product of two radicals. \(\frac{\sqrt[3]{(2x^2)^3}·\sqrt[3]{3x}}{\sqrt[3]{y^3}}\)
    Simplify. \(\frac{2x^2\sqrt[3]{3x}}{y}\)
    2. \(\sqrt[4]{\frac{48x^{10}}{y^8}}\)
    The fraction in the radicand cannot be simplified. Use the Quotient Property to write as two radicals. \(\frac{\sqrt[4]{48x^{10}}}{\sqrt[4]{y^8}}\)
    Rewrite each radicand as a product using perfect cube factors. \(\frac{\sqrt[4]{16x^8·3x^2}}{\sqrt[4]{y^8}}\)
    Rewrite the numerator as the product of two radicals. \(\frac{\sqrt[4]{(2x^2)^4}·\sqrt[4]{3x^2}}{\sqrt[4]{(y^2)^4}}\)
    Simplify. \(\frac{2x^2\sqrt[4]{3x^2}}{y^2}\)
    Example \(\PageIndex{35}\)

    Simplify:

    1. \(\sqrt[3]{\frac{108c^{10}}{d^6}}\)
    2. \(\sqrt[4]{\frac{80x^{10}}{y^5}}\).
    Answer
    1. \(\frac{3c^3\sqrt[3]{4c}}{d^2}\)
    2. \(\frac{x^2}{∣y∣}\sqrt[4]{\frac{80x^2}{y}}\)
    Example \(\PageIndex{36}\)

    Simplify:

    1. \(\sqrt[3]{\frac{40r^3}{s}}\)
    2. \(\sqrt[4]{\frac{162m^{14}}{n^{12}}}\)
    Answer
    1. \(r\sqrt[3]{\frac{40}{s}}\)
    2. \(\frac{3m^3\sqrt[4]{2m^2}}{∣n^3∣}\)

    Add and Subtract Higher Roots

    We can add and subtract higher roots like we added and subtracted square roots. First we provide a formal definition of like radicals.

    Definition: LIKE RADICALS

    Radicals with the same index and same radicand are called like radicals.

    Like radicals have the same index and the same radicand.

    • \(9\sqrt[4]{42x}\) and \(−2\sqrt[4]{42x}\) are like radicals.
    • \(5\sqrt[3]{125x}\) and \(6\sqrt[3]{125y}\) are not like radicals. The radicands are different.
    • \(2\sqrt[5]{1000q}\) and \(−4\sqrt[4]{1000q}\) are not like radicals. The indices are different.

    We add and subtract like radicals in the same way we add and subtract like terms. We can add \(9\sqrt[4]{42x}+(−2\sqrt[4]{42x})\) and the result is \(7\sqrt[4]{42x}\).

    Example \(\PageIndex{37}\)

    Simplify:

    1. \(\sqrt[3]{4x}+\sqrt[3]{4x}\)
    2. \(4\sqrt[4]{8}−2\sqrt[4]{8}\)
    Answer
    1. \(\sqrt[3]{4x}+\sqrt[3]{4x}\)
    The radicals are like, so we add the coefficients \(2\sqrt[3]{4x}\)
    2. \(4\sqrt[4]{8}−2\sqrt[4]{8}\)
    The radicals are like, so we subtract the coefficients. \(2\sqrt[4]{8}\)
    Example \(\PageIndex{38}\)

    Simplify:

    1. \(\sqrt[5]{3x}+\sqrt[5]{3x}\)
    2. \(3\sqrt[3]{9}−\sqrt[3]{9}\)
    Answer
    1. \(2\sqrt[5]{3x}\)
    2. \(2\sqrt[3]{9}\)
    Example \(\PageIndex{39}\)

    Simplify:

    1. \(\sqrt[4]{10y}+\sqrt[4]{10y}\)
    2. \(5\sqrt[6]{32}−3\sqrt[6]{32}\).
    Answer
    1. \(2\sqrt[4]{10y}\)
    2. \(2\sqrt[6]{32}\)

    When an expression does not appear to have like radicals, we will simplify each radical first. Sometimes this leads to an expression with like radicals.

    Example \(\PageIndex{40}\)

    Simplify:

    1. \(\sqrt[3]{54}−\sqrt[3]{16}\)
    2. \(\sqrt[4]{48}+\sqrt[4]{243}\).
    Answer
    1. \(\sqrt[3]{54}−\sqrt[3]{16}\)
    Rewrite each radicand using perfect cube factors. \(\sqrt[3]{27}·\sqrt[3]{2}−\sqrt[3]{8}·\sqrt[3]{2}\)
    Rewrite the perfect cubes. \(\sqrt[3]{(3)^3}·\sqrt[3]{2}−\sqrt[3]{(2)^3}·\sqrt[3]{2}\)
    Simplify the radicals where possible. \(3\sqrt[3]{2}−2\sqrt[3]{2}\)
    Combine like radicals. \(\sqrt[3]{2}\)
    2. \(\sqrt[4]{48}+\sqrt[4]{243}\)
    Rewrite using perfect fourth power factors. \(\sqrt[4]{16}·\sqrt[4]{3}+\sqrt[4]{81}·\sqrt[4]{3}\)
    Rewrite each radicand as a product using perfect cube factors. \(\sqrt[4]{(2)^4}·\sqrt[4]{3}+\sqrt[4]{(3)^4}·\sqrt[4]{3}\)
    Rewrite the numerator as the product of two radicals. \(2\sqrt[4]{3}+3\sqrt[4]{3}\)
    Simplify. \(5\sqrt[4]{3}\)
    Example \(\PageIndex{41}\)

    Simplify:

    1. \(\sqrt[3]{192}−\sqrt[3]{81}\)
    2. \(\sqrt[4]{32}+\sqrt[4]{512}\).
    Answer
    1. \(\sqrt[3]{3}\)
    2. \(6\sqrt[4]{2}\)
    Example \(\PageIndex{42}\)

    Simplify:

    1. \(\sqrt[3]{108}−\sqrt[3]{250}\)
    2. \(\sqrt[5]{64}+\sqrt[5]{486}\).
    Answer
    1. \(−\sqrt[3]{2}\)
    2. \(5\sqrt[5]{2}\)
    Example \(\PageIndex{43}\)

    Simplify:

    1. \(\sqrt[3]{24x^4}−\sqrt[3]{−81x^7}\)
    2. \(\sqrt[4]{162y^9}+\sqrt[4]{512y^5}\).
    Answer
    1. \(\sqrt[3]{24x^4}−\sqrt[3]{−81x^7}\)
    Rewrite each radicand using perfect cube factors. \(\sqrt[3]{8x^3}·\sqrt[3]{3x}−\sqrt[3]{−27x^6}·\sqrt[3]{3x}\)
    Rewrite the perfect cubes. \(\sqrt[3]{(2x)^3}·\sqrt[3]{3x}−\sqrt[3]{(−3x^2)^3}·\sqrt[3]{3x}\)
    Simplify the radicals where possible. \(2x\sqrt[3]{3x}−(−3x^2\sqrt[3]{3x})\)
    2. \(\sqrt[4]{162y^9}+\sqrt[4]{516y^5}\)
    Rewrite using perfect fourth power factors. \(\sqrt[4]{81y^8}·\sqrt[4]{2y}+\sqrt[4]{256y^4}·\sqrt[4]{2y}\)
    Rewrite each radicand as a product using perfect cube factors. \(\sqrt[4]{(3y^2)^4}·\sqrt[4]{2y}+\sqrt[4]{(4y)^4}·\sqrt[4]{2y}\)
    Rewrite the numerator as the product of two radicals. \(3y^2\sqrt[4]{2y}+4|y|\sqrt[4]{2y}\)
    Example \(\PageIndex{44}\)

    Simplify:

    1. \(\sqrt[3]{32y^5}−\sqrt[3]{−108y^8}\)
    2. \(\sqrt[4]{243r^{11}}+\sqrt[4]{768r^{10}}\).
    Answer
    1. \(2y\sqrt[3]{4y^2}+3y^2\sqrt[3]{4y^2}\)
    2. \(3r^2\sqrt[4]{3r^3}+4r^2\sqrt[4]{3r^2}\)
    Example \(\PageIndex{45}\)

    Simplify:

    1. \(\sqrt[3]{40z^7}−\sqrt[3]{−135z^4}\)
    2. \(\sqrt[4]{80s^{13}}+\sqrt[4]{1280s^6}\).
    Answer
    1. \(2z^2\sqrt[3]{5z}+3z^5\sqrt[3]{5z}\)
    2. \(2∣s^3∣\sqrt[4]{5s}+4|s|\sqrt[4]{5s}\)
    Access these online resources for additional instruction and practice with simplifying higher roots.
    • Simplifying Higher Roots
    • Add/Subtract Roots with Higher Indices

    Key Concepts

    • Properties of
    • \(\sqrt[n]{a}\) when n is an even number and
      • \(a \ge 0\), then \(\sqrt[n]{a}\) is a real number
      • \(a < 0\), then \(\sqrt[n]{a}\) is not a real number
      • When n is an odd number, \(\sqrt[n]{a}\) is a real number for all values of a.
      • For any integer \(n \ge 2\), when n is odd \(\sqrt[n]{a^n}=a\)
      • For any integer \(n \ge 2\), when n is even \(\sqrt[n]{a^n}=|a|\)
    • \(\sqrt[n]{a}\) is considered simplified if a has no factors of \(m^n\).
    • \(\sqrt[n]{ab}=\sqrt[n]{a}·\sqrt[n]{b}\) and \(\sqrt[n]{a}·\sqrt[n]{b}=\sqrt[n]{ab}\)
    • \(\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\) and \(\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}\)
    • To combine like radicals, simply add or subtract the coefficients while keeping the radical the same.

    Glossary

    nth root of a number
    If \(b^n=a\), then b is an nth root of a.
    principal nth root
    The principal nth root of a is written \(\sqrt[n]{a}\).
    index
    \(\sqrt[n]{a}\) n is called the index of the radical.
    like radicals
    Radicals with the same index and same radicand are called like radicals.

    This page titled 8.7: Higher Roots is shared under a CC BY license and was authored, remixed, and/or curated by OpenStax.

    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Section or Page
      Author
      OpenStax
      License
      CC BY
      Show Page TOC
      no
      Transcluded
      yes
    2. Tags
      1. source[1]-math-15189