In exercises 1 - 6, use the information provided to solve the problem.
1) Let \( w(x,y,z)=xy\cos z,\) where \( x=t,y=t^2,\) and \( z=\arcsin t.\) Find \( \dfrac{dw}{dt}\).
- Answer
- \( \dfrac{dw}{dt}=y\cos z+x\cos z(2t)−\dfrac{xy\sin z}{\sqrt{1−t^2}}\)
2) Let \( w(t,v)=e^{tv}\) where \( t=r+s\) and \( v=rs\). Find \( \dfrac{∂w}{∂r}\) and \( \dfrac{∂w}{∂s}\).
3) If \( w=5x^2+2y^2, \quad x=−3u+v,\) and \( y=u−4v,\) find \( \dfrac{∂w}{∂u}\) and \( \dfrac{∂w}{∂v}\).
- Answer
- \( \dfrac{∂w}{∂u}=−30x+4y \quad\ = \quad -30(-3u + v) + 4(u - 4v) \quad = \quad 90u -30v + 4u - 16v \quad = \quad 94u - 46v\),
\(\dfrac{∂w}{∂v}=10x−16y \quad\ = \quad 10(-3u + v) - 16(u - 4v) \quad = \quad -30u +10v - 16u + 64v \quad = \quad -46u + 74v\)
4) If \( w=xy^2,x=5\cos(2t),\) and \( y=5\sin(2t)\), find \( \dfrac{∂w}{∂t}\).
5) If \( f(x,y)=xy,x=r\cos θ,\) and \( y=r\sin θ\), find \(\dfrac{∂f}{∂r}\) and express the answer in terms of \( r\) and \( θ\).
- Answer
- \( \dfrac{∂f}{∂r}=r\sin(2θ)\)
6) Suppose \( f(x,y)=x+y,u=e^x\sin y,\quad x=t^2\) and \( y=πt\), where \( x=r\cos θ\) and \( y=r\sin θ\). Find \( \dfrac{∂f}{∂θ}\).
In exercises 7 - 12, find \( \dfrac{dz}{dt}\) in two ways, first using the chain rule and then by direct substitution.
7) \( z=x^2+y^2, \quad x=t,y=t^2\)
- Answer
- \( \dfrac{dz}{dt}=2t+4t^3\)
8) \( z=\sqrt{x^2+y^2},\quad y=t^2,x=t\)
9) \( z=xy,\quad x=1−\sqrt{t},y=1+\sqrt{t}\)
- Answer
- \( \dfrac{dz}{dt}=−1\)
10) \( z=\frac{x}{y},\quad x=e^t,y=2e^t\)
11) \( z=\ln(x+y), \quad x=e^t,y=e^t\)
- Answer
- \( \dfrac{dz}{dt}=1\)
12) \( z=x^4,\quad x=t,y=t\)
13) Let \( w(x,y,z)=x^2+y^2+z^2, \quad x=cost,y=sint,\) and \( z=e^t\). Express \( w\) as a function of \( t\) and find \( \dfrac{dw}{dt}\) directly. Then, find \( \dfrac{dw}{dt}\) using the chain rule.
- Answer
- \( \dfrac{dw}{dt}=2e^{2t}\) in both cases
14) Let \( z=x^2y,\) where \( x=t^2\) and \( y=t^3\). Find \( \dfrac{dz}{dt}\).
15) Let \( u=e^x\sin y,\) where \( x=-\ln 2t\) and \( y=πt\). Find \( \dfrac{du}{dt}\) when \( x=\ln 2\) and \( y=\frac{π}{4}\).
- Answer
- \( \dfrac{du}{dt} = \sqrt{2}\big(\pi - 4\big)\)
In exercises 16 - 33, find \( \dfrac{dy}{dx}\) using partial derivatives.
16) \( \sin(6x)+\tan(8y)+5=0\)
17) \( x^3+y^2x−3=0\)
- Answer
- \( \dfrac{dy}{dx}=−\dfrac{3x^2+y^2}{2xy}\)
18) \( \sin(x+y)+\cos(x−y)=4\)
19) \( x^2−2xy+y^4=4\)
- Answer
- \( \dfrac{dy}{dx}=\dfrac{y−x}{−x+2y^3}\)
20) \( xe^y+ye^x−2x^2y=0\)
21) \( x^{2/3}+y^{2/3}=a^{2/3}\)
- Answer
- \( \dfrac{dy}{dx}=−\sqrt[3]{\frac{y}{x}}\)
22) \( x\cos(xy)+y\cos x=2\)
23) \( e^{xy}+ye^y=1\)
- Answer
- \( \dfrac{dy}{dx}=−\dfrac{ye^{xy}}{xe^{xy}+e^y(1+y)}\)
24) \( x^2y^3+\cos y=0\)
25) Find \( \dfrac{dz}{dt}\) using the chain rule where \( z=3x^2y^3,\,\,x=t^4,\) and \( y=t^2\).
- Answer
- \( \dfrac{dz}{dt}=42t^{13}\)
26) Let \( z=3\cos x−\sin(xy),x=\frac{1}{t},\) and \( y=3t.\) Find \( \dfrac{dz}{dt}\).
27) Let \( z=e^{1−xy},\,\, x=t^{1/3},\) and \( y=t^3\). Find \( \dfrac{dz}{dt}\).
- Answer
- \( \dfrac{dz}{dt}=−\frac{10}{3}t^{7/3}×e^{1−t^{10/3}}\)
28) Find \( \dfrac{dz}{dt}\) by the chain rule where \( z=\cosh^2(xy),\,\,x=\frac{1}{2}t,\) and \( y=e^t\).
29) Let \( z=\dfrac{x}{y},\,\, x=2\cos u,\) and \( y=3\sin v.\) Find \( \dfrac{∂z}{∂u}\) and \( \dfrac{∂z}{∂v}\).
- Answer
- \( \dfrac{∂z}{∂u}=\dfrac{−2\sin u}{3\sin v}\) and \( \dfrac{∂z}{∂v}=\dfrac{−2\cos u\cos v}{3\sin^2v}\)
30) Let \( z=e^{x^2y}\), where \( x=\sqrt{uv}\) and \( y=\frac{1}{v}\). Find \( \dfrac{∂z}{∂u}\) and \( \dfrac{∂z}{∂v}\).
31) If \( z=xye^{x/y},\,\, x=r\cos θ,\) and \( y=r\sin θ\), find \( \dfrac{∂z}{∂r}\) and \( \dfrac{∂z}{∂θ}\) when \( r=2\) and \( θ=\frac{π}{6}\).
- Answer
- \( \dfrac{∂z}{∂r}=\sqrt{3}e^{\sqrt{3}}, \dfrac{∂z}{∂θ}=(2−4\sqrt{3})e^{\sqrt{3}}\)
32) Find \( \dfrac{∂w}{∂s}\) if \( w=4x+y^2+z^3,\,\,x=e^{rs^2},\,\,y=\ln(\frac{r+s}{t}),\) and \( z=rst^2\).
33) If \( w=\sin(xyz),\,\,x=1−3t,\,\,y=e^{1−t},\) and \( z=4t\), find \( \dfrac{∂w}{∂t}\).
- Answer
- \( \dfrac{∂w}{∂t}=-3yz\cos(xyz)−xze^{1−t}\cos(xyz)+4xy\cos(xyz)\)
In exercises 34 - 36, use this information: A function \( f(x,y)\) is said to be homogeneous of degree \( n\) if \( f(tx,ty)=t^nf(x,y)\). For all homogeneous functions of degree \( n\), the following equation is true: \( x\dfrac{∂f}{∂x}+y\dfrac{∂f}{∂y}=nf(x,y)\). Show that the given function is homogeneous and verify that \( x\dfrac{∂f}{∂x}+y\dfrac{∂f}{∂y}=nf(x,y)\).
34) \( f(x,y)=3x^2+y^2\)
35) \( f(x,y)=\sqrt{x^2+y^2}\)
- Answer
- \( f(tx,ty)=\sqrt{t^2x^2+t^2y^2}=t^1f(x,y), \quad \dfrac{∂f}{∂y}=x\frac{1}{2}(x^2+y^2)^{−1/2}×2x+y\frac{1}{2}(x^2+y^2)^{−1/2}×2y=1f(x,y)\)
36) \( f(x,y)=x^2y−2y^3\)
37) The volume of a right circular cylinder is given by \( V(x,y)=πx^2y,\) where \( x\) is the radius of the cylinder and \( y\) is the cylinder height. Suppose \( x\) and \( y\) are functions of \( t\) given by \( x=\frac{1}{2}t\) and \( y=\frac{1}{3}t\) so that \( x\) and \( y\) are both increasing with time. How fast is the volume increasing when \( x=2\) and \( y=5\)? Assume time is measured in seconds.
- Answer
- \( \ddfrac{dV}{dt} = \frac{34π}{3}\,\text{units}^3/\text{s}\)
38) The pressure \( P\) of a gas is related to the volume and temperature by the formula \( PV=kT\), where temperature is expressed in kelvins. Express the pressure of the gas as a function of both \( V\) and \( T\). Find \( \dfrac{dP}{dt}\) when \( k=1, \dfrac{dV}{dt}=2\) cm3/min, \( \dfrac{dT}{dt}=12\) K/min, \( V=20 cm^3\), and \( T=20°F\).
39) The radius of a right circular cone is increasing at \( 3\) cm/min whereas the height of the cone is decreasing at \( 2\) cm/min. Find the rate of change of the volume of the cone when the radius is \( 13\) cm and the height is \( 18\) cm.
- Answer
- \( \dfrac{dV}{dt}=\frac{1066π}{3}\,\text{cm}^3/\text{min}\)
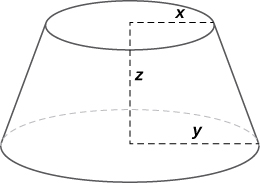
40) The volume of a frustum of a cone is given by the formula \( V=\frac{1}{3}πz(x^2+y^2+xy),\) where \( x\) is the radius of the smaller circle, \( y\) is the radius of the larger circle, and \( z\) is the height of the frustum (see figure). Find the rate of change of the volume of this frustum when \( x=10\) in., \(y=12\) in., and \( z=18\) in.
41) A closed box is in the shape of a rectangular solid with dimensions \( x,y,\) and \( z\). (Dimensions are in inches.) Suppose each dimension is changing at the rate of \( 0.5\) in./min. Find the rate of change of the total surface area of the box when \( x=2\) in., \(y=3\) in., and \( z=1\) in.
- Answer
- \( \dfrac{dA}{dt}=12\, \text{in.}^2/\text{min}\)
42) The total resistance in a circuit that has three individual resistances represented by \( x,y,\) and \( z\) is given by the formula \( R(x,y,z)=\dfrac{xyz}{yz+xz+xy}\). Suppose at a given time the \( x\) resistance is \( 100\,Ω\), the \( y\) resistance is \( 200\,Ω,\) and the \( z\) resistance is \( 300\,Ω.\) Also, suppose the \( x\) resistance is changing at a rate of \( 2\,Ω/\text{min},\) the \( y\) resistance is changing at the rate of \( 1\,Ω/\text{min}\), and the \( z\) resistance has no change. Find the rate of change of the total resistance in this circuit at this time.
43) The temperature \( T\) at a point \( (x,y)\) is \( T(x,y)\) and is measured using the Celsius scale. A fly crawls so that its position after \( t\) seconds is given by \( x=\sqrt{1+t}\) and \( y=2+\frac{1}{3}t\), where \( x\) and \( y\) are measured in centimeters. The temperature function satisfies \( T_x(2,3)=4\) and \( T_y(2,3)=3\). How fast is the temperature increasing on the fly’s path after \( 3\) sec?
- Answer
- \( 2\)°C/sec
44) The \( x\) and \( y\) components of a fluid moving in two dimensions are given by the following functions: \( u(x,y)=2y\) and \( v(x,y)=−2x\) with \(x≥0\) and \(y≥0\). The speed of the fluid at the point \( (x,y)\) is \( s(x,y)=\sqrt{u(x,y)^2+v(x,y)^2}\). Find \( \dfrac{∂s}{∂x}\) and \( \dfrac{∂s}{∂y}\) using the chain rule.
45) Let \( u=u(x,y,z),\) where \( x=x(w,t),\, y=y(w,t),\, z=z(w,t),\, w=w(r,s)\), and \( t=t(r,s).\) Use a tree diagram and the chain rule to find an expression for \( \dfrac{∂u}{∂r}\).
- Answer
- \( \frac{∂u}{∂r}=\frac{∂u}{∂x}(\frac{∂x}{∂w}\frac{∂w}{∂r}+\frac{∂x}{∂t}\frac{∂t}{∂r})+\frac{∂u}{∂y}(\frac{∂y}{∂w}\frac{∂w}{∂r}+\frac{∂y}{∂t}\frac{∂t}{∂r})+\frac{∂u}{∂z}(\frac{∂z}{∂w}\frac{∂w}{∂r}+\frac{∂z}{∂t}\frac{∂t}{∂r})\)


