4.13: Solve Equations with Fractions (Part 2)
- Last updated
- Save as PDF
- Page ID
- 21705
Solve Equations with a Fraction Coefficient
When we have an equation with a fraction coefficient we can use the Multiplication Property of Equality to make the coefficient equal to \(1\). For example, in the equation:
\[\dfrac{3}{4}x = 24 \nonumber \]
The coefficient of \(x\) is \(\dfrac{3}{4}\). To solve for \(x\), we need its coefficient to be \(1\). Since the product of a number and its reciprocal is \(1\), our strategy here will be to isolate \(x\) by multiplying by the reciprocal of \(\dfrac{3}{4}\). We will do this in Example \(\PageIndex{1}\).
Example \(\PageIndex{8}\): solve
Solve: \(\dfrac{3}{4}x = 24\).
Solution
| Multiply both sides by the reciprocal of the coefficient. | \(\textcolor{red}{\dfrac{4}{3}} \cdot \dfrac{3}{4} x = \textcolor{red}{\dfrac{4}{3}} \cdot 24 \) |
| Simplify. | \(1x = \dfrac{4}{3} \cdot \dfrac{24}{1} \) |
| Multiply. | \(x = 32 \) |
Check:
| Substitute x = 32. | \(\dfrac{3}{4} \cdot 32 \stackrel{?}{=} 24 \) |
| Rewrite 32 as a fraction. | \(\dfrac{3}{4} \cdot \dfrac{32}{1} \stackrel{?}{=} 24 \) |
| Multiply. The equation is true. | \(24 = 24 \; \checkmark\) |
Notice that in the equation \(\dfrac{3}{4} x = 24\), we could have divided both sides by \(\dfrac{3}{4}\) to get \(x\) by itself. Dividing is the same as multiplying by the reciprocal, so we would get the same result. But most people agree that multiplying by the reciprocal is easier.
Exercise \(\PageIndex{15}\)
Solve: \(\dfrac{2}{5}n = 14\).
- Answer
-
\(35\)
Exercise \(\PageIndex{16}\)
Solve: \(\dfrac{5}{6}y = 15\).
- Answer
-
\(18\)
Example \(\PageIndex{9}\): solve
Solve: \(− \dfrac{3}{8}w = 72\).
Solution
The coefficient is a negative fraction. Remember that a number and its reciprocal have the same sign, so the reciprocal of the coefficient must also be negative.
| Multiply both sides by the reciprocal of \(− \dfrac{3}{8}\). | \(\textcolor{red}{- \dfrac{8}{3}} \left(- \dfrac{3}{8} w \right) = \left(\textcolor{red}{- \dfrac{8}{3}}\right) 72 \) |
| Simplify; reciprocals multiply to one. | \(1w = - \dfrac{8}{3} \cdot \dfrac{72}{1} \) |
| Multiply. | \(w = -192\) |
Check:
| Let w = −192. | \(- \dfrac{3}{8} (-192) \stackrel{?}{=} 72 \) |
| Multiply. It checks. | \(72 = 72 \; \checkmark \) |
Exercise \(\PageIndex{17}\)
Solve: \(− \dfrac{4}{7}a = 52\).
- Answer
-
\(-91\)
Exercise \(\PageIndex{18}\)
Solve: \(− \dfrac{7}{9}w = 84\).
- Answer
-
\(-108\)
Translate Sentences to Equations and Solve
Now we have covered all four properties of equality—subtraction, addition, division, and multiplication. We’ll list them all together here for easy reference.
| Subtraction Property of Equality: For any real numbers a, b, and c, if a = b, then a − c = b − c. | Addition Property of Equality: For any real numbers a, b, and c, if a = b, then a + c = b + c. |
| Division Property of Equality: For any numbers a, b, and c, where c ≠ 0 if a = b, then \(\dfrac{a}{c} = \dfrac{b}{c}\). | Multiplication Property of Equality: For any real numbers a, b, and c if a = b, then ac = bc. |
When you add, subtract, multiply or divide the same quantity from both sides of an equation, you still have equality. In the next few examples, we’ll translate sentences into equations and then solve the equations. It might be helpful to review the translation table in Evaluate, Simplify, and Translate Expressions.
Example \(\PageIndex{10}\): solve
Translate and solve: \(n\) divided by \(6\) is \(−24\).
Solution
| Translate. | 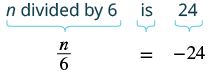 |
| Multiply both sides by 6. | \(\textcolor{red}{6} \cdot \dfrac{n}{6} = \textcolor{red}{6} (-24)\) |
| Simplify. | \(n = -144 \) |
| Check: | Is −144 divided by 6 equal to −24? |
| Translate. | \(\dfrac{-144}{6} \stackrel{?}{=} -24\) |
| Simplify. It checks. | \(-24 = -24 \; \checkmark \) |
Exercise \(\PageIndex{19}\)
Translate and solve: \(n\) divided by \(7\) is equal to \(−21\).
- Answer
-
\(\dfrac{n}{7} = -21\); \(n=-147\)
Exercise \(\PageIndex{20}\)
Translate and solve: \(n\) divided by \(8\) is equal to \(−56\).
- Answer
-
\(\dfrac{n}{8} = -56\); \(n=-448\)
Example \(\PageIndex{11}\): solve
Translate and solve: The quotient of \(q\) and \(−5\) is \(70\).
Solution
| Translate. |  |
| Multiply both sides by −5. | \(\textcolor{red}{-5} \left(\dfrac{q}{-5}\right) = \textcolor{red}{-5} (70) \) |
| Simplify. | \(q = -350\) |
| Check: | Is the quotient of −350 and −5 equal to 70? |
| Translate. | \(\dfrac{-350}{-5} \stackrel{?}{=} 70 \) |
| Simplify. It checks. | \(70 = 70 \; \checkmark \) |
Exercise \(\PageIndex{21}\)
Translate and solve: The quotient of \(q\) and \(−8\) is \(72\).
- Answer
-
\(\dfrac{q}{-8} = 72\); \(q=-576\)
Exercise \(\PageIndex{22}\)
Translate and solve: The quotient of \(p\) and \(−9\) is \(81\).
- Answer
-
\(\dfrac{p}{-9} = 81\); \(p=-729\)
Example \(\PageIndex{12}\): solve
Translate and solve: Two-thirds of \(f\) is \(18\).
Solution
| Translate. |  |
| Multiply both sides by \(\dfrac{3}{2}\). | \(\textcolor{red}{\dfrac{3}{2}} \cdot \dfrac{2}{3} f = \textcolor{red}{\dfrac{3}{2}} \cdot 18 \) |
| Simplify. | \(f = 27 \) |
| Check: | Is two-thirds of 27 equal to 18? |
| Translate. | \(\dfrac{2}{3} (27) \stackrel{?}{=} 18\) |
| Simplify. It checks. | \(18 = 18 \; \checkmark \) |
Exercise \(\PageIndex{23}\)
Translate and solve: Two-fifths of \(f\) is \(16\).
- Answer
-
\(\dfrac{2}{5}f = 16\); \(f=40\)
Exercise \(\PageIndex{24}\)
Translate and solve: Three-fourths of \(f\) is \(21\).
- Answer
-
\(\dfrac{3}{4}f = 21\); \(f=28\)
Example \(\PageIndex{13}\): solve
Translate and solve: The quotient of \(m\) and \(\dfrac{5}{6}\) is \(\dfrac{3}{4}\).
Solution
| Translate. | \(\dfrac{m}{\dfrac{5}{6}} = \dfrac{3}{4} \) |
| Multiply both sides by \(frac{5}{6}\) to isolate m. | \(\dfrac{5}{6} \left(\dfrac{m}{\dfrac{5}{6}}\right) = \dfrac{5}{6} \left(\dfrac{3}{4}\right) \) |
| Simplify. | \(m = \dfrac{5 \cdot 3}{6 \cdot 4}\) |
| Remove common factors and multiply. | \(m = \dfrac{5}{8} \) |
Check:
| Is the quotient of \(\dfrac{5}{8}\) and \(\dfrac{5}{6}\) equal to \(\dfrac{3}{4}\)? | \(\dfrac{\dfrac{5}{8}}{\dfrac{5}{6}} \stackrel{?}{=} \dfrac{3}{4} \) |
| Rewrite as division. | \(\dfrac{5}{8} \div \dfrac{5}{6} \stackrel{?}{=} \dfrac{3}{4} \) |
| Multiply the first fraction by the reciprocal of the second. | \(\dfrac{5}{8} \cdot \dfrac{6}{5} \stackrel{?}{=} \dfrac{3}{4} \) |
| Simplify. | \(\dfrac{3}{4} = \dfrac{3}{4} \; \checkmark \) |
Our solution checks.
Exercise \(\PageIndex{25}\)
Translate and solve. The quotient of \(n\) and \(\dfrac{2}{3}\) is \(\dfrac{5}{12}\).
- Answer
-
\(\dfrac{n}{\dfrac{2}{3}} = \dfrac{5}{12}\); \(n = \dfrac{5}{18}\)
Exercise \(\PageIndex{26}\)
Translate and solve. The quotient of \(c\) and \(\dfrac{3}{8}\) is \(\dfrac{4}{9}\).
- Answer
-
\(\dfrac{c}{\dfrac{3}{8}} = \dfrac{4}{9}\); \(c = \dfrac{1}{6}\)
Example \(\PageIndex{14}\): solve
Translate and solve: The sum of three-eighths and \(x\) is three and one-half.
Solution
| Translate. |  |
| Use the Subtraction Property of Equality to subtract \(\dfrac{3}{8}\) from both sides. | \(\dfrac{3}{8} + x - \dfrac{3}{8} = 3 \dfrac{1}{2} - \dfrac{3}{8} \) |
| Combine like terms on the left side. | \(x = 3 \dfrac{1}{2} - \dfrac{3}{8} \) |
| Convert mixed number to improper fraction. | \(x = 3 \dfrac{1}{2} - \dfrac{3}{8} \) |
| Convert to equivalent fractions with LCD of 8. | \(x = \dfrac{7}{2} - \dfrac{3}{8} \) |
| Subtract. | \(x = \dfrac{25}{8} \) |
| Write as a mixed number. | \(x = 3 \dfrac{1}{8} \) |
We write the answer as a mixed number because the original problem used a mixed number. Check: Is the sum of three-eighths and \(3 \dfrac{1}{8}\) equal to three and one-half?
| Add. | \(3 \dfrac{4}{8} \stackrel{?}{=} 3 \dfrac{1}{2} \) |
| Simplify. | \(3 \dfrac{1}{2} = 3 \dfrac{1}{2} \) |
The solution checks.
Exercise \(\PageIndex{27}\)
Translate and solve: The sum of five-eighths and \(x\) is one-fourth.
- Answer
-
\(\dfrac{5}{8}+x = \dfrac{1}{4}\); \(x = -\dfrac{3}{8}\)
Exercise \(\PageIndex{28}\)
Translate and solve: The difference of one-and-three-fourths and \(x\) is five-sixths.
- Answer
-
\(1\dfrac{3}{4} - x = \dfrac{5}{6}\); \(x = \dfrac{11}{12}\)
Access Additional Online Resources
- Solve One Step Equations With Fractions
- Solve One Step Equations With Fractions by Adding or Subtracting
- Solve One Step Equations With Fraction by Multiplying
Practice Makes Perfect
Determine Whether a Fraction is a Solution of an Equation
In the following exercises, determine whether each number is a solution of the given equation.
- x − \(\dfrac{2}{5}\) = \(\dfrac{1}{10}\):
- x = 1
- x = \(\dfrac{1}{2}\)
- x = \(− \dfrac{1}{2}\)
- y − \(\dfrac{1}{2}\) = \(\dfrac{5}{12}\):
- y = 1
- y = \(\dfrac{3}{4}\)
- y = \(- \dfrac{3}{4}\)
- h + \(\dfrac{3}{4}\) = \(\dfrac{2}{5}\):
- h = 1
- h = \(\dfrac{7}{20}\)
- h = \(- \dfrac{7}{20}\)
- k + \(\dfrac{2}{5}\) = \(\dfrac{5}{6}\):
- k = 1
- k = \(\dfrac{13}{30}\)
- k = \(- \dfrac{13}{30}\)
Solve Equations with Fractions using the Addition, Subtraction, and Division Properties of Equality
In the following exercises, solve.
- y + \(\dfrac{1}{3}\) = \(\dfrac{4}{3}\)
- m + \(\dfrac{3}{8}\) = \(\dfrac{7}{8}\)
- f + \(\dfrac{9}{10}\) = \(\dfrac{2}{5}\)
- h + \(\dfrac{5}{6}\) = \(\dfrac{1}{6}\)
- a − \(\dfrac{5}{8}\) = \(- \dfrac{7}{8}\)
- c − \(\dfrac{1}{4}\) = \(- \dfrac{5}{4}\)
- x − \(\left(- \dfrac{3}{20} \right)\) = \(- \dfrac{11}{20}\)
- z − \(\left(- \dfrac{5}{12} \right)\) = \(- \dfrac{7}{12}\)
- n − \(\dfrac{1}{6}\) = \(\dfrac{3}{4}\)
- p − \(\dfrac{3}{10}\) = \(\dfrac{5}{8}\)
- s + \(\left(- \dfrac{1}{2} \right)\) = \(- \dfrac{8}{9}\)
- k + \(\left(- \dfrac{1}{3} \right)\) = \(- \dfrac{4}{5}\)
- 5j = 17
- 7k = 18
- −4w = 26
- −9v = 33
Solve Equations with Fractions Using the Multiplication Property of Equality
In the following exercises, solve.
- \(\dfrac{f}{4}\) = −20
- \(\dfrac{b}{3}\) = −9
- \(\dfrac{y}{7}\) = −21
- \(\dfrac{x}{8}\) = −32
- \(\dfrac{p}{-5}\) = −40
- \(\dfrac{q}{-4}\) = −40
- \(\dfrac{r}{-12}\) = −6
- \(\dfrac{s}{-15}\) = −3
- −x = 23
- −y = 42
- −h = \(− \dfrac{5}{12}\)
- −k = \(− \dfrac{17}{20}\)
- \(\dfrac{4}{5}\)n = 20
- \(\dfrac{3}{10}\)p = 30
- \(\dfrac{3}{8}\)q = −48
- \(\dfrac{5}{2}\)m = −40
- \(- \dfrac{2}{9}\)a = 16
- \(- \dfrac{3}{7}\)b = 9
- \(- \dfrac{6}{11}\)u = −24
- \(- \dfrac{5}{12}\)v = −15
Mixed Practice
In the following exercises, solve.
- 3x = 0
- 8y = 0
- 4f = \(\dfrac{4}{5}\)
- 7g = \(\dfrac{7}{9}\)
- p + \(\dfrac{2}{3}\) = \(\dfrac{1}{12}\)
- q + \(\dfrac{5}{6}\) = \(\dfrac{1}{12}\)
- \(\dfrac{7}{8}\)m = \(\dfrac{1}{10}\)
- \(\dfrac{1}{4}\)n = \(\dfrac{7}{10}\)
- \(- \dfrac{2}{5}\) = x + \(\dfrac{3}{4}\)
- \(- \dfrac{2}{3}\) = y + \(\dfrac{3}{8}\)
- \(\dfrac{11}{20}\) = −f
- \(\dfrac{8}{15}\) = −d
Translate Sentences to Equations and Solve
In the following exercises, translate to an algebraic equation and solve.
- n divided by eight is −16.
- n divided by six is −24.
- m divided by −9 is −7.
- m divided by −7 is −8.
- The quotient of f and −3 is −18.
- The quotient of f and −4 is −20.
- The quotient of g and twelve is 8.
- The quotient of g and nine is 14.
- Three-fourths of q is 12.
- Two-fifths of q is 20.
- Seven-tenths of p is −63.
- Four-ninths of p is −28.
- m divided by 4 equals negative 6.
- The quotient of h and 2 is 43.
- Three-fourths of z is the same as 15.
- The quotient of a and \(\dfrac{2}{3}\) is \(\dfrac{3}{4}\).
- The sum of five-sixths and x is \(\dfrac{1}{2}\).
- The sum of three-fourths and x is \(\dfrac{1}{8}\).
- The difference of y and one-fourth is \(- \dfrac{1}{8}\).
- The difference of y and one-third is \(- \dfrac{1}{6}\).
Everyday Math
- Shopping Teresa bought a pair of shoes on sale for $48. The sale price was \(\dfrac{2}{3}\) of the regular price. Find the regular price of the shoes by solving the equation \(\dfrac{2}{3}\)p = 48
- Playhouse The table in a child’s playhouse is \(\dfrac{3}{5}\) of an adult-size table. The playhouse table is 18 inches high. Find the height of an adult-size table by solving the equation \(\dfrac{3}{5}\)h = 18.
Writing Exercises
- Example 4.100 describes three methods to solve the equation −y = 15. Which method do you prefer? Why?
- Richard thinks the solution to the equation \(\dfrac{3}{4}\)x = 24 is 16. Explain why Richard is wrong.
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
(b) Overall, after looking at the checklist, do you think you are well-prepared for the next Chapter? Why or why not?
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


