9.6: Use Properties of Rectangles, Triangles, and Trapezoids (Part 1)
- Last updated
- Save as PDF
- Page ID
- 21758
Learning Objectives
- Understand linear, square, and cubic measure
- Use properties of rectangles
- Use properties of triangles
- Use properties of trapezoids
be prepared!
Before you get started, take this readiness quiz.
- The length of a rectangle is 3 less than the width. Let w represent the width. Write an expression for the length of the rectangle. If you missed this problem, review Example 2.4.14.
- Simplify: \(\dfrac{1}{2}\)(6h). If you missed this problem, review Example 7.2.3.
- Simplify: \(\dfrac{5}{2}\)(10.3 − 7.9). If you missed this problem, review Example 5.5.9.
In this section, we’ll continue working with geometry applications. We will add some more properties of triangles, and we’ll learn about the properties of rectangles and trapezoids.
Understand Linear, Square, and Cubic Measure
When you measure your height or the length of a garden hose, you use a ruler or tape measure (Figure \(\PageIndex{1}\)). A tape measure might remind you of a line—you use it for linear measure, which measures length. Inch, foot, yard, mile, centimeter and meter are units of linear measure.

Figure \(\PageIndex{1}\) - This tape measure measures inches along the top and centimeters along the bottom.
When you want to know how much tile is needed to cover a floor, or the size of a wall to be painted, you need to know the area, a measure of the region needed to cover a surface. Area is measured is square units. We often use square inches, square feet, square centimeters, or square miles to measure area. A square centimeter is a square that is one centimeter (cm) on each side. A square inch is a square that is one inch on each side (Figure \(\PageIndex{2}\)).
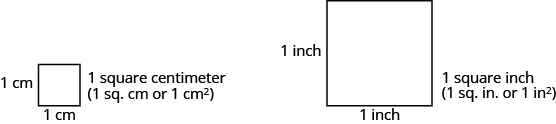
Figure \(\PageIndex{2}\) - Square measures have sides that are each 1 unit in length.
Figure \(\PageIndex{3}\) shows a rectangular rug that is 2 feet long by 3 feet wide. Each square is 1 foot wide by 1 foot long, or 1 square foot. The rug is made of 6 squares. The area of the rug is 6 square feet.

Figure \(\PageIndex{3}\) - The rug contains six squares of 1 square foot each, so the total area of the rug is 6 square feet.
When you measure how much it takes to fill a container, such as the amount of gasoline that can fit in a tank, or the amount of medicine in a syringe, you are measuring volume. Volume is measured in cubic units such as cubic inches or cubic centimeters. When measuring the volume of a rectangular solid, you measure how many cubes fill the container. We often use cubic centimeters, cubic inches, and cubic feet. A cubic centimeter is a cube that measures one centimeter on each side, while a cubic inch is a cube that measures one inch on each side (Figure \(\PageIndex{4}\)).
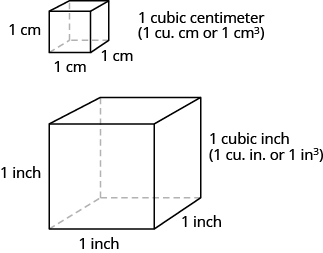
Figure \(\PageIndex{4}\) - Cubic measures have sides that are 1 unit in length.
Suppose the cube in Figure \(\PageIndex{5}\) measures 3 inches on each side and is cut on the lines shown. How many little cubes does it contain? If we were to take the big cube apart, we would find 27 little cubes, with each one measuring one inch on all sides. So each little cube has a volume of 1 cubic inch, and the volume of the big cube is 27 cubic inches.
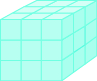
Figure \(\PageIndex{5}\) - A cube that measures 3 inches on each side is made up of 27 one-inch cubes, or 27 cubic inches.
Example \(\PageIndex{1}\):
For each item, state whether you would use linear, square, or cubic measure: (a) amount of carpeting needed in a room (b) extension cord length (c) amount of sand in a sandbox (d) length of a curtain rod (e) amount of flour in a canister (f) size of the roof of a doghouse.
Solution
| (a) You are measuring how much surface the carpet covers, which is the area. | square measure |
| (b) You are measuring how long the extension cord is, which is the length. | linear measure |
| (c) You are measuring the volume of the sand. | cubic measure |
| (d) You are measuring the length of the curtain rod. | linear measure |
| (e) You are measuring the volume of the flour. | cubic measure |
| (f) You are measuring the area of the roof. | square measure |
Exercise \(\PageIndex{1}\):
Determine whether you would use linear, square, or cubic measure for each item. (a) amount of paint in a can (b) height of a tree (c) floor of your bedroom (d) diameter of bike wheel (e) size of a piece of sod (f) amount of water in a swimming pool
- Answer a
-
cubic
- Answer b
-
linear
- Answer c
-
square
- Answer d
-
linear
- Answer e
-
square
- Answer f
-
cubic
Exercise \(\PageIndex{2}\):
Determine whether you would use linear, square, or cubic measure for each item. (a) volume of a packing box (b) size of patio (c) amount of medicine in a syringe (d) length of a piece of yarn (e) size of housing lot (f) height of a flagpole
- Answer a
-
cubic
- Answer b
-
square
- Answer c
-
cubic
- Answer d
-
linear
- Answer e
-
square
- Answer f
-
linear
Many geometry applications will involve finding the perimeter or the area of a figure. There are also many applications of perimeter and area in everyday life, so it is important to make sure you understand what they each mean.
Picture a room that needs new floor tiles. The tiles come in squares that are a foot on each side—one square foot. How many of those squares are needed to cover the floor? This is the area of the floor.
Next, think about putting new baseboard around the room, once the tiles have been laid. To figure out how many strips are needed, you must know the distance around the room. You would use a tape measure to measure the number of feet around the room. This distance is the perimeter.
Definition: Perimeter and Area
The perimeter is a measure of the distance around a figure.
The area is a measure of the surface covered by a figure.
Figure \(\PageIndex{6}\) shows a square tile that is 1 inch on each side. If an ant walked around the edge of the tile, it would walk 4 inches. This distance is the perimeter of the tile.
Since the tile is a square that is 1 inch on each side, its area is one square inch. The area of a shape is measured by determining how many square units cover the shape.
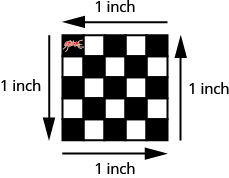
Figure \(\PageIndex{6}\) - Perimeter = 4 inches, Area = 1 square inch. When the ant walks completely around the tile on its edge, it is tracing the perimeter of the tile. The area of the tile is 1 square inch.
Example \(\PageIndex{2}\):
Each of two square tiles is 1 square inch. Two tiles are shown together. (a) What is the perimeter of the figure? (b) What is the area?

Solution
(a) The perimeter is the distance around the figure. The perimeter is 6 inches.
(b) The area is the surface covered by the figure. There are 2 square inch tiles so the area is 2 square inches.
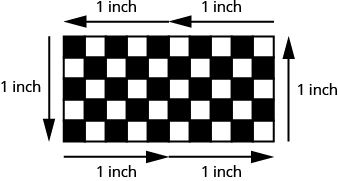
Exercise \(\PageIndex{3}\):
Find the (a) perimeter and (b) area of the figure:

- Answer a
-
8 inches
- Answer b
- 3 sq. inches
Exercise \(\PageIndex{4}\):
Find the (a) perimeter and (b) area of the figure:

- Answer a
-
8 centimeters
- Answer b
- 4 sq. centimeters
Use the Properties of Rectangles
A rectangle has four sides and four right angles. The opposite sides of a rectangle are the same length. We refer to one side of the rectangle as the length, L, and the adjacent side as the width, W. See Figure \(\PageIndex{7}\).
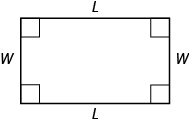
Figure \(\PageIndex{7}\) - A rectangle has four sides, and four right angles. The sides are labeled L for length and W for width.
The perimeter, P, of the rectangle is the distance around the rectangle. If you started at one corner and walked around the rectangle, you would walk L + W + L + W units, or two lengths and two widths. The perimeter then is
\[\begin{split} P = L + &W + L + W \\ &or \\ P = 2L &+ 2W \end{split}\]
What about the area of a rectangle? Remember the rectangular rug from the beginning of this section. It was 2 feet long by 3 feet wide, and its area was 6 square feet. See Figure \(\PageIndex{8}\). Since A = 2 • 3, we see that the area, A, is the length, L, times the width, W, so the area of a rectangle is A = L • W.
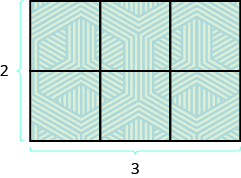
Figure \(\PageIndex{8}\) - The area of this rectangular rug is 6 square feet, its length times its width.
Definition: Properties of Rectangles
- Rectangles have four sides and four right (90°) angles.
- The lengths of opposite sides are equal.
- The perimeter, P, of a rectangle is the sum of twice the length and twice the width. See Figure 9.19.$$P = 2L + 2W$$
- The area, A, of a rectangle is the length times the width.$$A = L \cdot W$$
For easy reference as we work the examples in this section, we will restate the Problem Solving Strategy for Geometry Applications here.
HOW TO: USE A PROBLEM SOLVING STRATEGY FOR GEOMETRY APPLICATIONS
Step 1. Read the problem and make sure you understand all the words and ideas. Draw the figure and label it with the given information.
Step 2. Identify what you are looking for.
Step 3. Name what you are looking for. Choose a variable to represent that quantity.
Step 4. Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
Step 5. Solve the equation using good algebra techniques.
Step 6. Check the answer in the problem and make sure it makes sense.
Step 7. Answer the question with a complete sentence.
Example \(\PageIndex{3}\):
The length of a rectangle is 32 meters and the width is 20 meters. Find (a) the perimeter, and (b) the area.
Solution
(a)
| Step 1. Read the problem. Draw the figure and label it with the given information. | 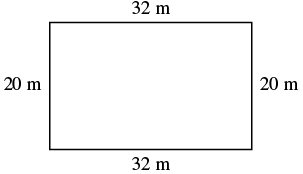 |
| Step 2. Identify what you are looking for. | the perimeter of a rectangle |
| Step 3. Name. Choose a variable to represent it. | Let P = the perimeter |
| Step 4. Translate. Write the appropriate formula. Substitute. | 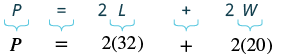 |
| Step 5. Solve the equation. | $$\begin{split} P &= 64 + 40 \\ P &= 104 \end{split}$$ |
| Step 6. Check. | $$\begin{split} P &\stackrel{?}{=} 104 \\ 20 + 32 + 20 + 32 &\stackrel{?}{=} 104 \\ 104 &= 104\; \checkmark \end{split}$$ |
| Step 7. Answer the question. | The perimeter of the rectangle is 104 meters. |
(b)
| Step 1. Read the problem. Draw the figure and label it with the given information. | 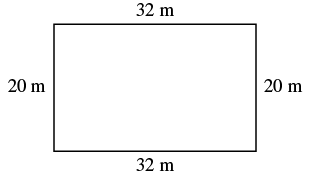 |
| Step 2. Identify what you are looking for. | the area of a rectangle |
| Step 3. Name. Choose a variable to represent it. | Let A = the area |
| Step 4. Translate. Write the appropriate formula. Substitute. | 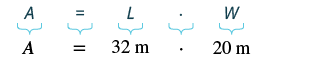 |
| Step 5. Solve the equation. | $$A = 640$$ |
| Step 6. Check. | $$\begin{split} A &\stackrel{?}{=} 640 \\ 32 \cdot 20 &\stackrel{?}{=} 640 \\ 640 &= 640\; \checkmark \end{split}$$ |
| Step 7. Answer the question. | The area of the rectangle is 60 square meters. |
Exercise \(\PageIndex{5}\):
The length of a rectangle is 120 yards and the width is 50 yards. Find (a) the perimeter and (b) the area.
- Answer a
-
340 yd
- Answer b
- 6000 sq. yd
Exercise \(\PageIndex{6}\):
The length of a rectangle is 62 feet and the width is 48 feet. Find (a) the perimeter and (b) the area.
- Answer a
-
220 ft
- Answer b
- 2976 sq. ft
Example \(\PageIndex{4}\):
Find the length of a rectangle with perimeter 50 inches and width 10 inches.
Solution
| Step 1. Read the problem. Draw the figure and label it with the given information. | 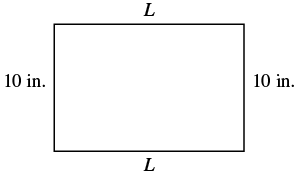 |
| Step 2. Identify what you are looking for. | the length of the rectangle |
| Step 3. Name. Choose a variable to represent it. | Let L = the length |
| Step 4. Translate. Write the appropriate formula. Substitute. | 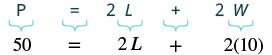 |
| Step 5. Solve the equation. | $$\begin{split} 50 \textcolor{red}{-20} &= 2L + 20 \textcolor{red}{-20} \\ 30 &= 2L \\ \dfrac{30}{\textcolor{red}{2}} &= \dfrac{2L}{\textcolor{red}{2}} \\ 15 &= L \end{split}$$ |
| Step 6. Check. | $$\begin{split} P &\stackrel{?}{=} 50 \\ 15 + 10 + 15 + 10 &\stackrel{?}{=} 50 \\ 50 &= 50\; \checkmark \end{split}$$ |
| Step 7. Answer the question. | The length is 15 inches. |
Exercise \(\PageIndex{7}\):
Find the length of a rectangle with a perimeter of 80 inches and width of 25 inches.
- Answer
-
15 inches
Exercise \(\PageIndex{8}\):
Find the length of a rectangle with a perimeter of 30 yards and width of 6 yards.
- Answer
-
9 yd
In the next example, the width is defined in terms of the length. We’ll wait to draw the figure until we write an expression for the width so that we can label one side with that expression.
Example \(\PageIndex{5}\):
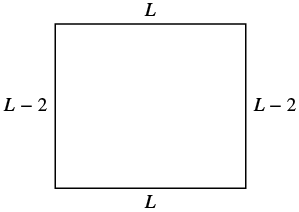
The width of a rectangle is two inches less than the length. The perimeter is 52 inches. Find the length and width.
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | the length and width of the rectangle |
| Step 3. Name. Choose a variable to represent it. Now we can draw a figure using these expressions for the length and width. |
Since the width is defined in terms of the length, we let L = length. The width is two feet less that the length, so we let L − 2 = width.
|
| Step 4. Translate. Write the appropriate formula. The formula for the perimeter of a rectangle relates all the information. Substitute in the given information. | 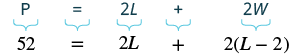 |
| Step 5. Solve the equation. | $$52 = 2L + 2L - 4$$ |
| Combine like terms. | $$52 = 4L - 4$$ |
| Add 4 to each side. | $$56 = 4L$$ |
| Divide by 4. | $$\begin{split} \dfrac{56}{4} &= \dfrac{4L}{4} \\ 14 &= L \\ 14 &= L \end{split}$$The length is 14 inches. |
| Now we need to find the width. The width is L − 2. | $$\begin{split} &L - 2 \\ &\textcolor{red}{14} - 2 \\ &12 \end{split}$$The width is 12 inches. |
| Step 6. Check. | Since 14 + 12 + 14 + 12 = 52 , this works! |
| Step 7. Answer the question. | The length is 14 feet and the width is 12 feet. |
Exercise \(\PageIndex{9}\):
The width of a rectangle is seven meters less than the length. The perimeter is 58 meters. Find the length and width.
- Answer
-
18 m, 11 m
Exercise \(\PageIndex{10}\):
The length of a rectangle is eight feet more than the width. The perimeter is 60 feet. Find the length and width.
- Answer
-
11 ft, 19 ft
Example \(\PageIndex{6}\):
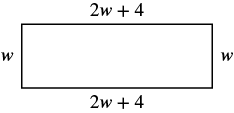
The length of a rectangle is four centimeters more than twice the width. The perimeter is 32 centimeters. Find the length and width.
Solution
| Step 1. Read the problem. | |
| Step 2. Identify what you are looking for. | the length and width |
| Step 3. Name. Choose a variable to represent it. |
let W = width The length is four more than twice the width. 2w + 4 = length
|
| Step 4. Translate. Write the appropriate formula and substitute in the given information. | 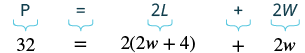 |
| Step 5. Solve the equation. | $$\begin{split} 32 &= 4w + 8 + 2w \\ 32 &= 6w + 8 \\ 24 &= 6w \\ 4 &= w\quad width \\ 2w &+ 4\quad length \\ 2(\textcolor{red}{4}) &+ 4 \\ 12&\quad The\; length\; is\; 12\; cm \ldotp \end{split}$$ |
| Step 6. Check. | $$\begin{split} p &= 2L + 2W \\ 32 &\stackrel{?}{=} 2 \cdot 12 + 2 \cdot 4 \\ 32 &= 32\; \checkmark \end{split}$$ |
| Step 7. Answer the question. | The length is 12 cm and the width is 4 cm. |
Exercise \(\PageIndex{11}\):
The length of a rectangle is eight more than twice the width. The perimeter is 64 feet. Find the length and width.
- Answer
-
8 ft, 24 ft
Exercise \(\PageIndex{12}\):
The width of a rectangle is six less than twice the length. The perimeter is 18 centimeters. Find the length and width.
- Answer
-
5 cm, 4 cm
Example \(\PageIndex{7}\):
The area of a rectangular room is 168 square feet. The length is 14 feet. What is the width?
Solution
| Step 1. Read the problem. | 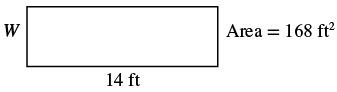 |
| Step 2. Identify what you are looking for. | the width of a rectangular room |
| Step 3. Name. Choose a variable to represent it. | Let W = width |
| Step 4. Translate. Write the appropriate formula and substitute in the given information. | $$\begin{split} A &= LW \\ 168 &= 14W \end{split}$$ |
| Step 5. Solve the equation. | $$\begin{split} \dfrac{168}{14} &= \dfrac{14W}{14} \\ 12 &= W \end{split}$$ |
| Step 6. Check. | $$\begin{split} A &= LW \\ 168 &\stackrel{?}{=} 14 \cdot 12 \\ 168 &= 168\; \checkmark \end{split}$$ |
| Step 7. Answer the question. | The width of the room is 12 feet. |
Exercise \(\PageIndex{13}\):
The area of a rectangle is 598 square feet. The length is 23 feet. What is the width?
- Answer
-
26 ft
Exercise \(\PageIndex{14}\):
The width of a rectangle is 21 meters. The area is 609 square meters. What is the length?
- Answer
-
29 m
Example \(\PageIndex{8}\):
The perimeter of a rectangular swimming pool is 150 feet. The length is 15 feet more than the width. Find the length and width.
Solution
| Step 1. Read the problem. Draw the figure and label it with the given information. | 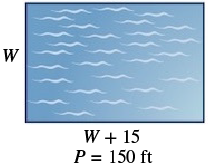 |
| Step 2. Identify what you are looking for. | the length and width of the pool |
| Step 3. Name. Choose a variable to represent it. The length is 15 feet more than the width. |
Let W = width W + 15 = length |
| Step 4. Translate. Write the appropriate formula and substitute. | 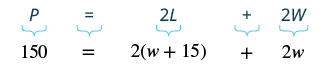 |
| Step 5. Solve the equation. | $$\begin{split} 150 &= 2w + 30 + 2w \\ 150 &= 4w + 30 \\ 120 &= 4w \\ 30 &= w\quad the\; width\; of\; the\; pool \\ w &+ 15\quad the\; length\; of\; the\; pool \\ \textcolor{red}{30} &+ 15 \\ 45& \end{split}$$ |
| Step 6. Check. | $$\begin{split} p &= 2L + 2W \\ 150 &\stackrel{?}{=} 2(45) + 2(30) \\ 150 &= 150\; \checkmark \end{split}$$ |
| Step 7. Answer the question. | The length of the pool is 45 feet and the width is 30 feet. |
Exercise \(\PageIndex{15}\):
The perimeter of a rectangular swimming pool is 200 feet. The length is 40 feet more than the width. Find the length and width.
- Answer
-
30 ft, 70 ft
Exercise \(\PageIndex{16}\):
The length of a rectangular garden is 30 yards more than the width. The perimeter is 300 yards. Find the length and width.
- Answer
-
60 yd, 90 yd
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."