7.R: Introduction to Calculus (Review)
- Last updated
- Save as PDF
- Page ID
- 79069
12.1: Finding Limits - Numerical and Graphical Approaches
For the exercises 1-6, use the Figure below.
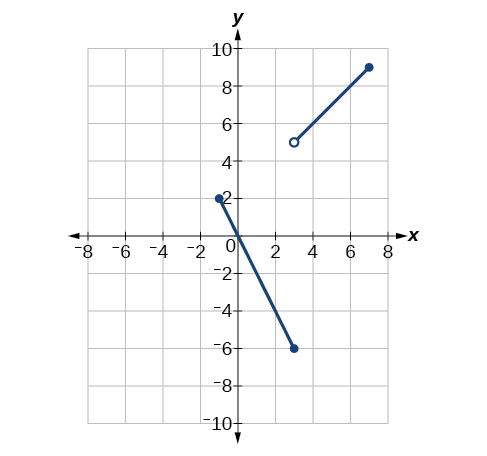
1) \(\lim \limits_{x \to -1^+}f(x)\)
- Answer
-
\(2\)
2) \(\lim \limits_{x \to -1^-}f(x)\)
3) \(\lim \limits_{x \to -1}f(x)\)
- Answer
-
does not exist
4) \(\lim \limits_{x \to 3}f(x)\)
5) At what values of \(x\) is the function discontinuous? What condition of continuity is violated?
- Answer
-
Discontinuous at \(x=-1\left (\lim \limits_{x \to a}f(x) \text{ does not exist} \right )\), \(x=3\left (\text{ jump discontinuity} \right )\), and \(x=7\left (\lim \limits_{x \to a}f(x) \text{ does not exist} \right )\).
6) Using the Table below, estimate \(\lim \limits_{x \to 0}f(x)\).
| \(x\) | \(F(x)\) |
|---|---|
| −0.1 | 2.875 |
| −0.01 | 2.92 |
| −0.001 | 2.998 |
| 0 | Undefined |
| 0.001 | 2.9987 |
| 0.01 | 2.865 |
| 0.1 | 2.78145 |
| 0.15 | 2.678 |
- Answer
-
\(3\)
For the exercises 7-9, with the use of a graphing utility, use numerical or graphical evidence to determine the left- and right-hand limits of the function given as \(x\) approaches \(a\). If the function has limit as \(x\) approaches \(a\), state it. If not, discuss why there is no limit.
7) \(f(x)=\begin{cases} \left | x \right |-1 & \text{ if } x\neq 1 \\ x^3 & \text{ if } x= 1 \end{cases} a=1\)
8) \(f(x)=\begin{cases} \dfrac{1}{x+1} & \text{ if } x= -2 \\ (x+1)^2 & \text{ if } x\neq -2 \end{cases} a=-2\)
- Answer
-
\(\lim \limits_{x \to -2}f(x)=1\)
9) \(f(x)=\begin{cases} \sqrt{x+3} & \text{ if } x<1 \\ -\sqrt[3]{x} & \text{ if } x>1 \end{cases} a=1\)
12.2: Finding Limits - Properties of Limits
For the exercises 1-6, find the limits if \(\lim \limits_{x \to c} f(x)=-3\) and \(\lim \limits_{x \to c} g(x)=5\).
1) \(\lim \limits_{x \to c} (f(x)+g(x))\)
- Answer
-
\(2\)
2) \(\lim \limits_{x \to c} \dfrac{f(x)}{g(x)}\)
3) \(\underset{x \to c}{\lim } (f(x)\cdot g(x))\)
- Answer
-
\(-15\)
4) \(\lim \limits_{x \to 0^+} f(x), f(x)=\begin{cases} 3x^2+2x+1 & x>0 \\ 5x+3 & x<0 \end{cases}\)
5) \(\lim \limits_{x \to 0^-} f(x), f(x)=\begin{cases} 3x^2+2x+1 & x>0 \\ 5x+3 & x<0 \end{cases}\)
- Answer
-
\(3\)
6) \(\lim \limits_{x \to 3^+} (3x-〚x〛)\)
For the exercises 7-11, evaluate the limits using algebraic techniques.
7) \(\lim \limits_{h \to 0} \left ( \dfrac{(h+6)^2-36}{h} \right )\)
- Answer
-
\(12\)
8) \(\lim \limits_{x \to 25} \left ( \dfrac{x^2-625}{\sqrt{x}-5} \right )\)
9) \(\lim \limits_{x \to 1} \left ( \dfrac{-x^2-9x}{x} \right )\)
- Answer
-
\(-10\)
10) \(\lim \limits_{x \to 4} \left ( \dfrac{7-\sqrt{12x+1}}{x-4} \right )\)
11) \(\lim \limits_{x \to 3} \left ( \dfrac{\frac{1}{3}+\frac{1}{x}}{3+x} \right )\)
- Answer
-
\(-\dfrac{1}{9}\)
12.3: Continuity
For the exercises 1-5, use numerical evidence to determine whether the limit exists at \(x=a\). If not, describe the behavior of the graph of the function at \(x=a\).
1) \(f(x)=\dfrac{-2}{x-4};\; a=4\)
2) \(f(x)=\dfrac{-2}{(x-4)^2};\; a=4\)
- Answer
-
At \(x=4\), the function has a vertical asymptote.
3) \(f(x)=\dfrac{-x}{x^2-x-6};\; a=3\)
4) \(f(x)=\dfrac{6x^2+23x+20}{4x^2-25};\; a=-\dfrac{5}{2}\)
- Answer
-
removable discontinuity at \(a=-\dfrac{5}{2}\)
5) \(f(x)=\dfrac{\sqrt{x}-3}{9-x};\; a=9\)
For the exercises 6-12, determine where the given function \(f(x)\) is continuous. Where it is not continuous, state which conditions fail, and classify any discontinuities.
6) \(f(x)=x^2-2x-15\)
- Answer
-
continuous on \((-\infty, \infty)\)
7) \(f(x)=\dfrac{x^2-2x-15}{x-5}\)
8) \(f(x)=\dfrac{x^2-2x}{x^2-4x+4}\)
- Answer
-
removable discontinuity at \(x=2\). \(f(2)\) is not defined, but limits exist.
9) \(f(x)=\dfrac{x^3-125}{2x^2-12x+10}\)
10) \(f(x)=\dfrac{x^2-\frac{1}{x}}{2-x}\)
- Answer
-
discontinuity at \(x=0\) and \(x=2\). Both \(f(0)\) and \(f(2)\) are not defined.
11) \(f(x)=\dfrac{x+2}{x^2-3x-10}\)
12) \(f(x)=\dfrac{x+2}{x^3+8}\)
- Answer
-
removable discontinuity at \(x=-2\). \(f(-2)\) is not defined.
12.4: Derivatives
For the exercises 1-5, find the average rate of change \(f(x)=\dfrac{f(x+h)-f(x)}{h}\).
1) \(f(x)=3x+2\)
2) \(f(x)=5\)
- Answer
-
\(0\)
3) \(f(x)=\dfrac{1}{x+1}\)
4) \(f(x)=\ln (x)\)
- Answer
-
\(f(x)=\dfrac{\ln (x+h)-\ln (x)}{h}\)
5) \(f(x)=e^{2x}\)
For the exercises 6-7, find the derivative of the function.
6) \(f(x)=4x-6\)
- Answer
-
\(4\)
7) \(f(x)=5x^2-3x\)
8) Find the equation of the tangent line to the graph of \(f(x)\) at the indicated \(x\) value. \[f(x)=-x^3+4x;\; x=2 \nonumber \]
- Answer
-
\(y=-8x+16\)
9) For the following exercise, with the aid of a graphing utility, explain why the function is not differentiable everywhere on its domain. Specify the points where the function is not differentiable. \[f(x)=\dfrac{x}{\left | x \right |} \nonumber \]
10) Given that the volume of a right circular cone is \(V=\dfrac{1}{3}\pi r^2h\) and that a given cone has a fixed height of \(9\) cm and variable radius length, find the instantaneous rate of change of volume with respect to radius length when the radius is \(2\) cm. Give an exact answer in terms of \(π\).
- Answer
-
\(12\pi \)
Practice Test
For the exercises 1-6, use the graph of \(f\) in the Figure below.
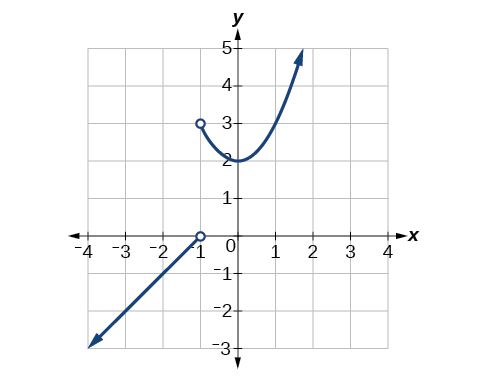
1) \(f(1)\)
- Answer
-
\(3\)
2) \(\lim \limits_{x \to -1^+} f(x)\)
3) \(\lim \limits_{x \to -1^-} f(x)\)
- Answer
-
\(0\)
4) \(\lim \limits_{x \to -1} f(x)\)
5) \(\lim \limits_{x \to -2} f(x)\)
- Answer
-
\(-1\)
6) At what values of \(x\) is \(f\) discontinuous? What property of continuity is violated?
7) \(f(x)=\begin{cases} \dfrac{1}{3}-3 & \text{ if } x\leq 2 \\ x^3+1 & \text{ if } x>2 \end{cases} a=2\)
- Answer
-
\(\lim \limits_{x \to 2^-} f(x)=-\dfrac{5}{2}a\) and \(\lim \limits_{x \to 2^+} f(x)=9\)
8) \(f(x)=\begin{cases} x^3+1 & \text{ if } x<1 \\ 3x^2-1 & \text{ if } x=1\; a=1 \\ -\sqrt{x+3}+4 & \text{ if } x>1 \end{cases}\)
For the exercises 9-11, evaluate each limit using algebraic techniques.
9) \(\lim \limits_{x \to -5} \left ( \dfrac{\frac{1}{5}+\frac{1}{x}}{10+2x} \right )\)
- Answer
-
\(-\dfrac{1}{50}\)
10) \(\lim \limits_{h \to 0} \left ( \dfrac{\sqrt{h^2+25}-5}{h^2} \right )\)
11) \(\lim \limits_{h \to 0} \left ( \dfrac{1}{h}-\dfrac{1}{h^2+h} \right )\)
- Answer
-
\(1\)
For the exercises 12-13, determine whether or not the given function \(f\) is continuous. If it is continuous, show why. If it is not continuous, state which conditions fail.
12) \(f(x)=\sqrt{x^2-4}\)
13) \(f(x)=\dfrac{x^3-4x^2-9x+36}{x^3-3x^2+2x-6}\)
- Answer
-
removable discontinuity at \(x=3\)
For the exercises 14-16, use the definition of a derivative to find the derivative of the given function at \(x=a\).
14) \(f(x)=\dfrac{3}{5+2x}\)
15) \(f(x)=\dfrac{3}{\sqrt{x}}\)
- Answer
-
\(f'(x)=-\dfrac{3}{2a^{\frac{3}{2}}}\)
16) \(f(x)=2x^2+9x\)
17) For the graph in the Figure below, determine where the function is continuous/discontinuous and differentiable/not differentiable.
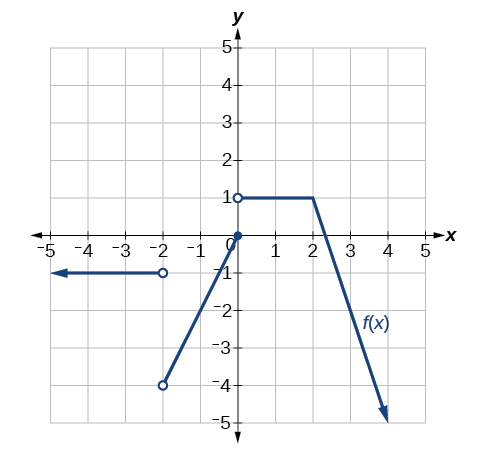
- Answer
-
discontinuous at \(-2,0\), not differentiable at \(-2,0, 2\).
For the exercises 18-19, with the aid of a graphing utility, explain why the function is not differentiable everywhere on its domain. Specify the points where the function is not differentiable.
18) \(f(x)=\left | x-2 \right | - \left | x+2 \right |\)
19) \(f(x)=\dfrac{2}{1+e^{\frac{2}{x}}}\)
- Answer
-
not differentiable at \(x=0\) (no limit)
For the exercises 20-24, explain the notation in words when the height of a projectile in feet, \(s\), is a function of time \(t\) in seconds after launch and is given by the function \(s(t)\).
20) \(s(0)\)
21) \(s(2)\)
- Answer
-
the height of the projectile at \(t=2\) seconds
22) \(s'(2)\)
23) \(\dfrac{s(2)-s(1)}{2-1}\)
- Answer
-
the average velocity from \(t=1\) to \(t=2\)
24) \(s(t)=0\)
For the exercises 25-28, use technology to evaluate the limit.
25) \(\lim \limits_{x \to 0}\dfrac{\sin (x)}{3x}\)
- Answer
-
\(\dfrac{1}{3}\)
26) \(\lim \limits_{x \to 0}\dfrac{\tan ^2(x)}{2x}\)
27) \(\lim \limits_{x \to 0}\dfrac{\sin (x)(1-\cos (x))}{2x^2}\)
- Answer
-
\(0\)
28) Evaluate the limit by hand.
\[\lim \limits_{x \to 1}f(x), \text{ where } f(x)=\begin{cases} 4x-7 & x\neq 1 \\ x^2-4 & x= 1 \end{cases} \nonumber \]
At what value(s) of \(x\) is the function below discontinuous?
\[f(x)=\begin{cases} 4x-7 & x\neq 1 \\ x^2-4 & x= 1 \end{cases} \nonumber \]
For the exercises 29-32, consider the function whose graph appears in Figure.
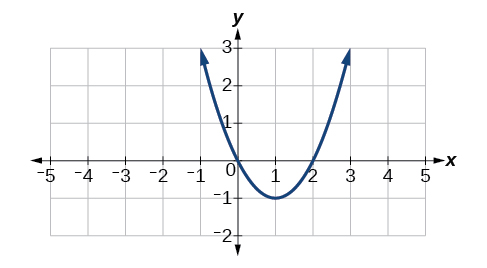
29) Find the average rate of change of the function from \(x=1\) to \(x=3\).
- Answer
-
\(2\)
30) Find all values of \(x\) at which \(f'(x)=0\).
- Answer
-
\(x=1\)
31) Find all values of \(x\) at which \(f'(x)\) does not exist.
32) Find an equation of the tangent line to the graph of \(f\) the indicated point: \(f(x)=3x^2-2x-6,\; x=-2\)
- Answer
-
\(y=-14x-18\)
For the exercises 33-34, use the function \(f(x)=x(1-x)^{\frac{2}{5}}\)
33) Graph the function \(f(x)=x(1-x)^{\tfrac{2}{5}}\) by entering \(f(x)=x\left ((1-x)^2 \right )^{\tfrac{1}{5}}\) and then by entering \(f(x)=x\left ((1-x)^{\tfrac{1}{5}} \right )^2\).
34) Explore the behavior of the graph of \(f(x)\) around \(x=1\) by graphing the function on the following domains, \([0.9, 1.1], [0.99, 1.01], [0.999, 1.001]\), and \([0.9999, 1.0001]\). Use this information to determine whether the function appears to be differentiable at \(x=1\).
- Answer
-
The graph is not differentiable at \(x=1\) (cusp).
For the exercises 35-42, find the derivative of each of the functions using the definition: \(\lim \limits_{h \to 0} \dfrac{f(x+h)-f(x)}{h}\)
35) \(f(x)=2x-8\)
36) \(f(x)=4x^2-7\)
- Answer
-
\(f'(x)=8x\)
37) \(f(x)=x-\dfrac{1}{2}x^2\)
38) \(f(x)=\dfrac{1}{x+2}\)
- Answer
-
\(f'(x)=-\dfrac{1}{(2+x)^2}\)
39) \(f(x)=\dfrac{3}{x-1}\)
40) \(f(x)=-x^3+1\)
- Answer
-
\(f'(x)=-3x^2\)
41) \(f(x)=x^2+x^3\)
42) \(f(x)=\sqrt{x-1}\)
- Answer
-
\(f'(x)=-\dfrac{1}{2\sqrt{x-1}}\)
Contributors and Attributions
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.


