9.1: Digital Roots and Divisibility
- Last updated
- Save as PDF
- Page ID
- 83018
It's helpful to understand what is meant by the DIGITAL ROOT of a number because they are used in divisibility tests, and are also used for checking arithmetic problem. A DIGITAL ROOT of a number is one of these digits: 0, 1, 2, 3, 4, 5, 6, 7 or 8.
Definition: The DIGITAL ROOT of a number is the remainder obtained when a number is divided by 9.
Exercise 1
Divide each of the following numbers by 9. Then, write the remainder.
| a. 25 | h. 8 |
| b. 48 | i. 54 |
| c. 53 | j. 74 |
| d. 829 | k. 481 |
| e. 5402 | l. 936 |
| f. 3455 | m. 8314 |
| g. 47522 | n. 647 |
Below is another easier way to find the digital root of a number.
Step 1: Add the individual digits of the number.
Step 2: If there is more than one digit after adding all the digits, repeat this process until you get a single digit. If the final sum is 9, write 0, because 9 and 0 are equivalent in digital roots (since the remainder is a number smaller than 9). That is why the digital root of a number is only one of these digits: 0, 1, 2, 3, 4, 5, 6, 7 or 8. Those are the only possible remainders that can be obtained when a number is divided by 9! It can't be 9. The single digit you finally end up with is the DIGITAL ROOT of the number.
Examples: Find the digital roots of the following numbers.
Example 1: 34
34: Add the digits: 3 + 4 = 7
The digital root of 34 is 7
Example 2: 321
321: Add the digits: 3 + 2 + 1 = 6
The digital root of 321 is 6
Example 3: 58
58: Add the digits: 5 + 8 = 13 Add the digits again: 1 + 3 = 4
The digital root of 58 is 4
Example 4: 97
97: Add the digits: 9 + 7 = 16 Add the digits again: 1 + 6 = 7
The digital root of 97 is 7
Example 5: 72
72: Add the digits: 7 + 2 = 9 In digital roots, 9 is the same as 0
The digital root of 72 is 0
Example 6: 346,721
346,721: Add the digits, we get 3 + 4 + 6 + 7 + 2 + 1= 23
Add the digits again: 2 + 3 = 5
The digital root of 346,725 is 5
Note that you should not write 97 = 16 = 7. 97 IS NOT EQUAL to 7!! The digital root of 97 is equal to 7. I use dashes, colons or arrows to record the digital root, so it looks something like this: 346,721 \(\rightarrow\) 23 \(\rightarrow\) 5. Don't use equal signs!!!
Another method for finding digital roots uses the fact that 9 and 0 are equivalent in digital roots. The process of finding digital roots is also called Casting out Nines. When you add the digits, you don't have to add the digit 9 or any combination of numbers that add up to 9 (like 2 and 7, or 5 and 4, or 2 and 3 and 4, etc.) – you can "cast out" all 9's. Cross them off; then add the remaining digits together. The following example illustrates how "casting out nines" simplifies the process of finding the digital root of a large number.
Example
Find the digital root of 5,624,398.
Without casting out nines: 5 + 6 + 2 + 4 + 3 + 9 + 8 = 37. Add again: 3 + 7 = 10. Add again: 1 + 0 = 1.
Casting out Nines: Since 5 and 4 add up to 9, cross them off: \(\not{5}, 6, \not{24}, \not{398}\). Since 6 and 3 add up to 9, also cross them off: \(\not{5}, \not{6}, \not{24}, \not{398}\). Also cross off the 9: \(\not{5}, \not{6}, \not{24}, \not{398}\). The only digits to add are the 2 and 8, which is 10. The digital root of 10 is 1. So 1 is the digital root of 5,624,398 which is the same answer obtained without first casting out nines.
Below, the digital roots for examples 4, 5 and 6 on the previous page is computed again using casting out nines. Note that the digital root remains the same.
Example 4: 97
97: Cross off the 9. Only the 7 remains. The digital root is 7.
Example 5: 72
72: 7 + 2 = 9, so cross them off. Therefore, the digital root is 0.
Example 6: 346,721
346,721: Cross off the 3 and 6, and also the 7 and 2. The only digits to add are the 4 and 1. Therefore, the digital root is 5.
Exercise 2
Find the digital roots of the following numbers, using either method. Remember that 9 is not a digital root. Write zero (0) if the sum is 9 (cast out the 9).
| a. 25 | h. 8 |
| b. 48 | i. 54 |
| c. 53 | j. 74 |
| d. 829 | k. 481 |
| e. 5402 | l. 936 |
| f. 3455 | m. 8314 |
| g. 47522 | n. 647 |
Exercise 3
Did you obtain the same answers for exercises 1 and 2?
Note: This method of finding the digital root only has to do with the number 9. You can't find the remainder of a number when dividing by 7 by adding the digits.
Using Digital Roots is to Check Addition and Multiplication Problems.
To check an addition problem, add the digital roots of the addends. Then, check to see if the digital root of that sum is the same as the digital root of the actual sum of the addends. This works whether there are only two addends, or several addends.
Below are some examples of how to check addition. The actual addition is shown to the left. Arrows are used to show the digital roots of the addends and sum. To check, the digital roots of the addends are added together, and then the digital root of that sum is computed. Compare it to the digital root of the actual sum. If they are equal, put a check to indicate the answer is probably correct. NOTE: There is a slight chance that the digital roots match, but the answer is still not correct due to some other mistake, like transposing digits. For instance, in example 1 below, it's possible someone might write down 1153 for the answer. The digital roots in the check would match. The possibility of this happening is slight, so we generally assume the problem was done correctly if the digital roots check. On the other hand, if the digital roots do not check, you know it is wrong.
Example 1
\(\begin{aligned} 723 & \rightarrow 3 \\ \underline{+ 412} & \rightarrow 7 \\ 1135 & \rightarrow 1 \end{aligned}\)
Ck: 3 + 7 = 10 \(\rightarrow\) 1 \(\surd\) Correct!
Explanation: To check, add the digital root of the addends (3 + 7 = 10); then find the digital root of 10 (1). Verify that this equals the digital root of the sum, 1135 (1). Since it does, the addition problem was probably done correctly.
Example 2
\(\begin{aligned} 463 & \rightarrow 4 \\ \underline{+ 529} & \rightarrow 7 \\ 1630 & \rightarrow 1 \end{aligned}\)
Ck: 4 + 7 = 11 \(\rightarrow\) 2 Wrong!
Explanation: To check, add the digital root of the addends (4 + 7 = 11); then find the digital root of 11 (2). This should equal the digital root of the sum, 1630 (1). Since it doesn't , there is a mistake and the addition problem was done incorrectly.
Exercise 4
Someone did the following addition problems, but only wrote down the answers. Check the answer to each problem by using digital roots. Note that the procedure is the same if there are more than two addends. Add the digital roots of all the addends. Show Work!
| a. \(\begin{aligned} 4983 \\ \underline{+ 6829} \\ 10802 \end{aligned}\) | b. \(\begin{aligned} 5567 \\ \underline{+ 4987} \\ 10554 \end{aligned}\) | c. \(\begin{aligned} 3467 \\ \underline{+ 2541} \\ 5908 \end{aligned}\) |
| d. \(\begin{aligned} 8972 \\ 8876 \\ \underline{+ 5873} \\ 23721 \end{aligned}\) | e. \(\begin{aligned} 5873 \\ 3674 \\ \underline{+ 4763} \\ 13260 \end{aligned}\) | f. \(\begin{aligned} 4789 \\ 9835 \\ \underline{+ 5301} \\ 19925 \end{aligned}\) |
For a multiplication problem, the check is similar, except to check, you multiply the digital roots of the numbers you are multiplying. To check addition, you ADD the digital roots of the addends and check against the digital root of the sum. To check multiplication, you MULTIPLY the digital root of the numbers being multiplied and check against the digital root of the product. Here are some examples that provide an answer someone might have written down after doing the multiplication problem on another piece of paper.
Example 1
\(\begin{aligned} 85 & \rightarrow 13 \rightarrow 4 \\ \underline{\times 63} & \rightarrow 0 \\ 5355 & \rightarrow 18 \rightarrow 0 \end{aligned}\)
Ck: \(4 \times 0 = 0\) Correct!
Explanation: To check, multiply the digital roots of the numbers you are multiplying (\(4 \times 0 = 0\)); then find the digital root of 0 (0). Verify that it equals the digital root of the product, 5355 (0). Since it does, the multiplication problem was probably done correctly.
Example 2
\(\begin{aligned} 43 & \rightarrow 7 \\ \underline{\times 52} & \rightarrow 7 \\ 2136 & \rightarrow 3 \end{aligned}\)
Ck: \(7 \times 7 = 49\) \(\rightarrow\) 4 Incorrect!
Explanation: To check, multiply the digital roots of the numbers you are multiplying (\(7 \times 7 = 49\)); then find the digital root of 49 (4). This should equal the digital root of the product, 2136 (3). Since it doesn't , there is a mistake. Therefore, the multiplication problem was done incorrectly.
Exercise 5
Someone did the following multiplication problems, but only wrote down the answers. Check the answer to each problem by using digital roots. Show Work!
| a. \(\begin{aligned} 74 \\ \underline{\times 53} \\ 3922 \end{aligned}\) | b. \(\begin{aligned} 29 \\ \underline{\times 36} \\ 944 \end{aligned}\) | c. \(\begin{aligned} 68 \\ \underline{\times 28} \\ 1904 \end{aligned}\) |
| d. \(\begin{aligned} 65 \\ \underline{\times 79} \\ 5125 \end{aligned}\) | e. \(\begin{aligned} 81 \\ \underline{\times 55} \\ 4455 \end{aligned}\) | f. \(\begin{aligned} 48 \\ \underline{\times 52} \\ 2596 \end{aligned}\) |
| g. \(\begin{aligned} 569 \\ \underline{\times 61} \\ 34709 \end{aligned}\) | h. \(\begin{aligned} 653 \\ \underline{\times 524} \\ 242172 \end{aligned}\) | i. \(\begin{aligned} 2333 \\ \underline{\times 1203} \\ 2806599 \end{aligned}\) |
Exercise 6
Add or multiply the following as indicated, then use digital roots to check the answer to each problem. Show Work!
| a. \(\begin{aligned} 7362 \\ \underline{+ 5732} \end{aligned}\) | b. \(\begin{aligned} 8308 \\ \underline{ + 956} \end{aligned}\) |
| d. \(\begin{aligned} 6784 \\ \underline{ + 6835} \end{aligned}\) | e. \(\begin{aligned} 9994 \\ \underline{ + 8721} \end{aligned}\) |
| f. \(\begin{aligned} 57 \\ \underline{\times 8} \end{aligned}\) | g. \(\begin{aligned} 34 \\ \underline{\times 7} \end{aligned}\) |
| g. \(\begin{aligned} 87 \\ \underline{\times 52} \end{aligned}\) | h. \(\begin{aligned} 825 \\ \underline{\times 13} \end{aligned}\) |
Using Digital Roots is to Check Subtraction Problems.
To check subtraction, you usually add the difference (the answer) to the subtrahend (the number that was subtracted) and see if you get the minuend (the number you subtracted from). In other words, to check that 215 – 134 = 81 was done correctly, simply add 81 and 134, which is 215. To check subtraction using digital roots, simply add the digital root of the difference to the digital root of the subtrahend and see if you get the digital root of the minuend. To check that 215 – 134 = 81 was done correctly, simply add the digital roots 81 and 134: 0 + 8 = 8. Verify that 8 is the digital root of the minuend, 215. It is! Here is another example. Let's say someone did the following subtraction problem: 5462 – 2873 = 2589. To check, add the digital roots of 2589 and 2873, or 6 + 2 to get 8. Since 8 is also the digital root of 5462, the answer is probably correct.
Here are some more examples of how to check subtraction using digital roots.
Example 1
\(\begin{aligned} 7362 & \rightarrow 0 \\ \underline{ – 5732} & \rightarrow 8 \\ 1630 & \rightarrow 1 \end{aligned}\)
Ck: 1 + 8 = 9 \(\rightarrow\) 0 \(\surd\) Correct!
Explanation: To check, add the digital root of the difference and subtrahend (1 + 8 = 9). The digital root of 9 is 0. Verify that this equals the digital root of the minuend, 7632 (0). Since it does, the subtraction was probably done correctly.
Example 2
\(\begin{aligned} 5073 & \rightarrow 6 \\ \underline{ – 878} & \rightarrow 5 \\ 4205 & \rightarrow 2 \end{aligned}\)
Ck: 2 + 5 = 7 WRONG!
Explanation: To check, add the digital root of the difference and subtrahend (2 + 5 = 7). This should equal the digital root of the minuend, 5073 (6). Since it doesn't, the subtraction was not done correctly.
Exercise 7
Someone did the following subtractions problems, but only wrote down the answers. Check the answer to each problem by using digital roots. Show Work!
| a. \(\begin{aligned} 572 \\ \underline{– 356} \\ 216 \end{aligned}\) | b. \(\begin{aligned} 296 \\ \underline{– 189} \\ 107 \end{aligned}\) | c. \(\begin{aligned} 501 \\ \underline{– 327} \\ 284 \end{aligned}\) |
| d. \(\begin{aligned} 3217 \\ \underline{– 2391} \\ 926 \end{aligned}\) | e. \(\begin{aligned} 3546 \\ \underline{– 1138} \\ 2408 \end{aligned}\) | f. \(\begin{aligned} 7502 \\ \underline{– 4729} \\ 2773 \end{aligned}\) |
Exercise 8
Subtract, add or multiply the following as indicated, then use digital roots to check the answer to each problem. Show Work!
| a. \(\begin{aligned} 7362 \\ \underline{– 5732} \end{aligned}\) | b. \(\begin{aligned} 8308 \\ \underline{– 956} \end{aligned}\) |
| d. \(\begin{aligned} 6784 \\ \underline{– 6335} \end{aligned}\) | e. \(\begin{aligned} 9994 \\ \underline{– 8721} \end{aligned}\) |
| f. \(\begin{aligned} 557 \\ \underline{+ 348} \end{aligned}\) | g. \(\begin{aligned} 834 \\ \underline{+ 767} \end{aligned}\) |
| h. \(\begin{aligned} 48 \\ \underline{\times 6} \end{aligned}\) | i. \(\begin{aligned} 13 \\ \underline{\times 29} \end{aligned}\) |
Using Digital Roots is to Check Division Problems.
To check division, you multiply the divisor (the number you are dividing by) by the quotient (the answer), and then add the remainder. It is correct if the answer obtained is equal to the dividend (the number you divided into). In other words, here is how to check this division, \(431 \div 34 = 12\)r. 23: Multiply 34 by 12 and add 23. Here are the steps: \(34 \times 12 + 23 = 408 + 23 = 431\). Since 431 is the dividend, this problem was done correctly. To check division using digital roots, simply multiply the digital root of the divisor by the digital root of the quotient, and add the digital root of the remainder. If the digital root of that number equals the digital root of the dividend, it is probably correct.
Note: After the digital roots of the divisor and quotient are multiplied, you can first find the digital root of that product before adding the digital root of the remainder.
Here is how to check the division problem we did above by using digital roots. Multiply the digital root of the divisor, 34, by the digital root of the quotient, 12: \(7 \times 3 = 21\). Then add the digital root of the remainder, 23: 21 + 5 = 26. Determine the digital root of that number, 26, which is 8. Check to see if 8 matches the digital root of the dividend, 431. It does. As stated in the note, you could determine the digital root of 21 before adding the digital root of the remainder. In this case, it would have looked like this: \(7 \times 3 = 21 \rightarrow 3\). Then add the digital root of the remainder, 23: 3 + 5 = 8. Verify that this equals the digital root of the dividend, 431. It does. Therefore, the division was probably done correctly. More examples follow. The check without digital roots is shown to the right. The digital root check is shown under the division problem.
Example 1

Example 2
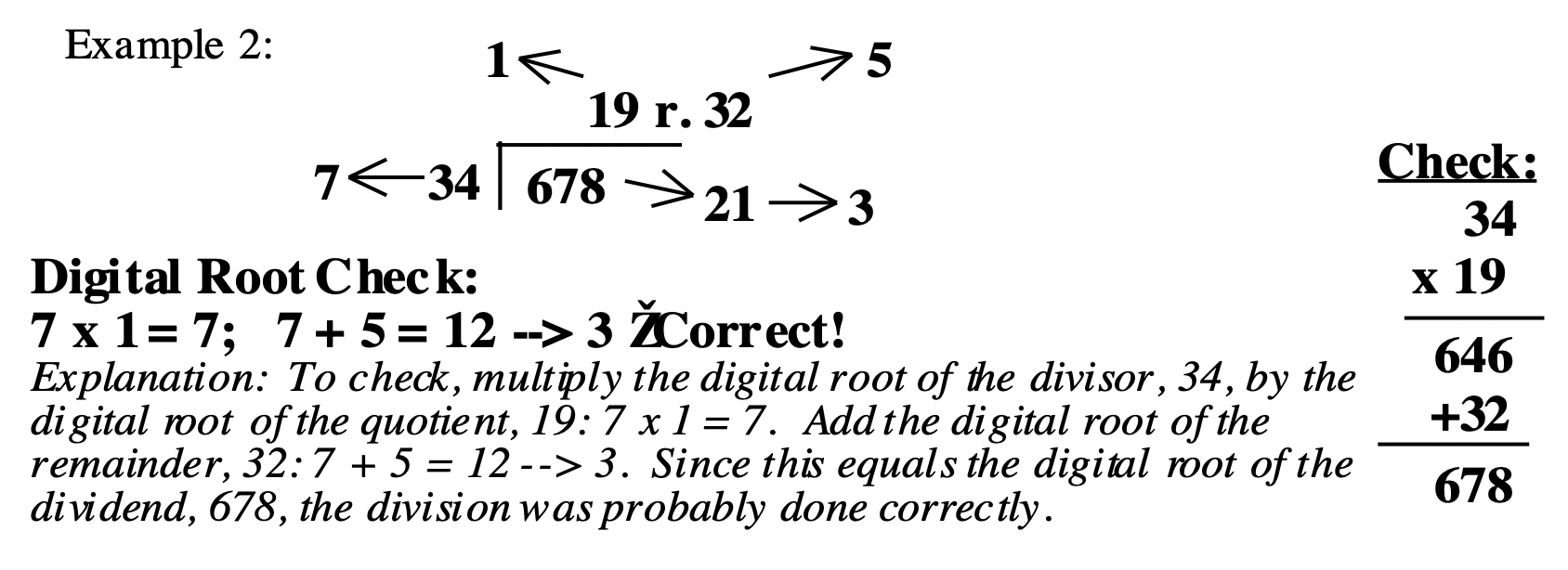
Below is one more example for you to study.
Example 3

Exercise 9
Someone did the following division problems, but only wrote down the answers. Check the answer to each problem by using digital roots. Show work. You don't need to do the actual check as shown to the right of the last three examples. Show work!
|
a. 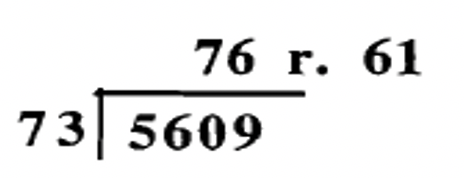 |
b. 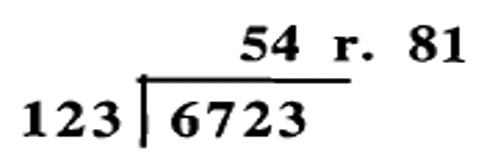 |
|
c. 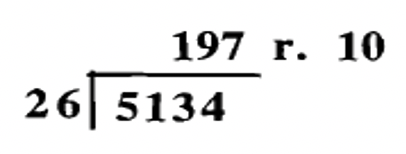 |
d. 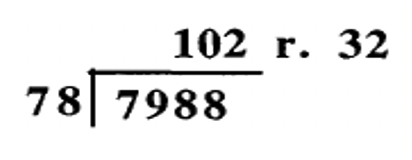 |
One more note of caution about using digital roots:
In problem 9d, a common mistake some people make is to forget to put the zero in the quotient, 102. Instead, the answer might have been written as 12 r. 32. Using digital roots, the answer would check. So, you should also check the reasonableness of the answer by approximating. For instance, \(78 \times 12\) is about 80 times 10 or 800, which is not even close to equaling the dividend, 7988. Another time digital roots might fail is when someone transposes the digits of a number. If the answer to a problem was 465, and it was written as 456, using digital roots wouldn't detect the mistake.
Exercise 10
Do the following division problem, and check the answer using digital roots. Show work.
\(23972 \div 156\) = ____________
Later in this module, we will explore prime numbers, composite numbers, the greatest common factor of two or more numbers, and the least common multiple of two or more numbers. Factoring is the method used to find the prime factorization of a composite number, and it can also be used to find the greatest common factor and least common multiple of a set of numbers. One of the problems in factoring large numbers is that sometimes it isn't clear if it is prime or composite. In other words, it isn't clear whether it has any factors other than 1 or itself. Most of us know that if the last digit of a numeral is even, then 2 will divide into it; or if it ends in 0, 10 will divide into it; or if it ends in 0 or 5, that 5 will divide into it. Sometimes, people even have trouble determining if relatively small numbers are prime. For instance, many people think 91 is prime, but in fact it is not. Knowing some divisibility tests makes the task easier, so we'll soon take some time to discuss divisibility tests for several numbers. First, we need to go over some notation concerning divisibility.
When you see 12/3, this means 12 "divided by" 3. The slash that slants to the right is another way to write the division sign, \(\div\). 12/3 (or \(12 \div 3\)) is a division problem, and the answer is 4.
Here is something altogether different. If I say "3 divides 12", I am making a statement. "3 divides 12" is not a division problem that needs to be done. It is a statement that happens to be true. The symbol used to represent the word "divides" is a vertical line. So, "3 divides 12" can be written "3|12". Again, this is a statement, a fact, not a division problem. The way to express "does not divide" is to put a slash through the symbol: \(\not{l}\)
So, how do I know "3 divides 12" is a true statement? The definition of "divides" follows:
Definition: "a divides b" if there exists a whole number, n, such that an = b. This is simply saying that "a divides b" means a is a factor of b! In shorthand notation, this is written "a|b if there exists a whole number, n, such that an = b, or a|b means that a is a factor of b."
Okay, so what exactly does "there exists a whole number, n, such that an = b" mean? Well, it means that the first number times some whole number equals the second number. Or you can think "a divides b" is true if \(b \div a\) is a whole number.
Let's get back to why "3 divides 12" is a true statement. Hmmm...you can be formal and ask yourself: Is there a whole number n such that 3n = 12? Or, you can simply ask yourself: Is 3 a factor (or divisor) of 12? In either case, the answer is yes, so the statement is true.
Let's work a little more on the difference between a statement using "divides", and an actual division problem.
Examples: Determine if each of the following is a statement or if it is a division problem. If it is a statement, state if it is true or false and back up your answer. If it is a division problem, state the answer to the division problem.
Example 1: 4|20
4|20
Solution
This is a true statement, because 4 is a factor of 20 (since \(4 \cdot 5 = 20\))
Example 2: 20/6
20/6
Solution
This is a division problem. The answer is 3 r. 2
Example 3: 15|3
15|3
Solution
This is a false statement because 15 is not a factor of 3
Example 4: 6 divides 20
6 divides 20
Solution
This is a false statement because 6 is not a factor of 20
Example 5: 3 divides 21
3 divides 21
Solution
This is a true statement because 3 is a factor of 21 (since \(3 \cdot 7 = 21\))
Exercise 11
Determine if each of the following is a statement or if it is a division problem. If it is a statement, then decide if it is true or false and back up your answer. If it is a division problem, state the answer to the division problem. Study the examples on the previous page if you need help getting started.
| a. 35/7 |
| b. 35|7 |
| c. 7|35: |
| d. 40/7 |
| e. 56|8 |
| f. 7|40: |
| g. 12 divides 60 |
| h. 80 divided by 30 |
| i. 70 divided by 5 |
| j. 42 divides 3 |
| k. 6 divides 42 |
| l. 80 divided by 10 |
| m. 100/2 |
| n. 4|100 |
| o. 4|90: |
| p. 25|5 |
Let's go back to the formal definition of "divides":
Definition: a|b if there exists a whole number, n, such that an = b.
We need to use this formal notation in order to do some proofs. Consider the following:
Example 1
Is the following statement true? If a|b and a|c, then a|(b+c).
a|b and a|c means that a is a factor of b and a is also a factor of c. We must determine if that necessarily implies that a is also a factor of the sum, b + c. The first line of strategy is to test it out on a few numbers, and see if you can find a counterexample. If you find a counterexample, the answer is no and you are done. If you can't find a counterexample, maybe it is true. If you think it is true, you must PROVE it by being general and formal.
I would start by picking any number for a, like a = 3, and then choose numbers for b and c for which 3 is a factor, like 15 and 18. Plug them in: "If 3|15 and 3|18, does 3|(15+18)?" Since 3|33, the answer is yes. It looks like this statement might be true.
Exercise 12
Choose different numbers for a, b and c in "If a|b and a|c, then a|(b+c)" to see if the statement seems to be true.
The statement, "If a|b and a|c, then a|(b+c)", happens to be true. You must write a proof to prove that it is always true. Here is one way to write a formal proof:
Example 1
Is the following statement true?: If a|b and a|c, then a|(b+c).
Solution
If a|b, then an = b for some whole number, n. If a|c, then am = c for some whole number, m. Using these substitutions for b and c, we get that a|(b + c) is true if a|(an + am) which is true if a is a factor of an + am. Factor: an + am = a(n + m). This clearly shows that a is indeed a factor of an + am. Therefore, if a|b and a|c, then a|(b+c).
Exercise 13
Write a formal proof to show that the following is true: If x|y and x|z, then x|(y + z).
Example 2
Is the following statement true? If a|(b+c), then a|b and a|c.
a|(b + c) means that a is a factor of the sum, b + c. The question asks if that necessarily implies that a is a factor of b and also a factor of c. The first line of strategy is to test it out on a few numbers, and see if you can find a counterexample, or if it looks like it is true. If you find a counterexample, the answer is no and you are done. If you think it is true, you must PROVE it by being general and formal.
Start by picking any number for a, like a = 3 and picking a number for the sum b + c, for which 3 is a factor, like 15 or 18, etc. Let b + c = 15. Note that there are many combinations of numbers that add up to 15: 1 + 14, 2 + 13, 3 + 12, 7 + 8, etc. You are being asked if 3 divides into the sum of any two whole numbers, will it necessarily divide into each individual addend as well? For instance, if you broke 15 up as the sum of 9 and 6, this would be the statement: "If 3|(9 + 6), then 3|9 and 3|6." Using these numbers, it is true and you haven't found a counterexample. Try splitting up 15 another way, perhaps as the sum of 10 and 5. Then, the statement becomes: "If 3|(10 + 5), then 3|10 and 3|5." The answer is no, and therefore these numbers may be used as a counterexample, which proves the statement is false. Remember: In order for a statement to be true, it must be for all values of a and b. On the other hand, only one counterexample showing it is not true is sufficient to prove a statement is false.
Exercise 14
Consider the statement: "If a|(b+c), then a|b and a|c." Provide an example using numbers other than a = 3, b = 9 and c = 6 that makes it look like this statement might be true.
Exercise 15
Consider the statement: "If a|(b+c), then a|b and a|c." Provide a counterexample using numbers other than a = 3, b = 10 and c = 5 to show this statement is false.
Exercise 16
Consider the statement: "If a|c and b|c, then (a + b)|c." Provide a counterexample to show this statement is false.
Exercise 17
Consider the statement: "If (a + b)|c, then a|c and b|c." Provide a counterexample to show this statement is false.
Exercise 18
Prove that the following statement is true: "If a|b and a|c, then a|(bc)"
Example
Prove that the following statement is true: "If a|b and a|(b + c), then a|c"
Solution
If a|b, then am = b for some whole number, m. If a|(b + c), then an = b + c for some whole number, n. Keep in mind that since b and c are positive, then (b + c) > b, which means n > m. We are trying to prove that a is a factor of c. Since am = b, we can substitute am for b into the equation an = b + c, which means an = am + c. Solving for c, this is equivalent to an – am = c. So if a is a factor of an – am, then a is a factor of c. Factor: an – am = a(n – m). This clearly shows a is a factor of an – am, which means a is a factor of c. Therefore, the statement "If a|b and a|(b + c), then a|c" is true. (Note: n – m must be a whole number since n and m are whole numbers and n > m.)
Exercise 19
Prove that the following statement is true: "If c|a and c|(a + b), then c|b"
Okay, finally on to the divisibility tests. We will use our new notation for divides (|).
All counting numbers can be considered factors of zero. In other words, for all counting numbers, m, m|0 is always true since there is always some number times m that equals zero, namely zero itself.
Assume n is a positive whole number. The following are divisibility tests to determine what numbers divide into n, or what numbers are factors of n.
Divisibility Test for 2: 2|n if the last digit of n is even (0, 2, 4, 6, or 8)
Examples
Use the divisibility test for 2 to determine if the following is true or false
1. 2|97
This is false because the last digit (7) is not even
2. 2|356
This is true because the last digit (6) is even
Divisibility Test for 4: (think of 4 as \(2^{\mathbf{2}}\))
4|n if 4|(the number represented by the last two digits of n)
Examples
Use the divisibility test for 4 to determine if the following is true or false.
1. 4|527
This is false because 4 does not divide 27, (since 4 is not a factor of 27).
2. 4|25,356
This is true because 4|56.
3. 4|624
This is true because 4|24.
Divisibility Test for 8: (think of 8 as \(2^{\mathbf{3}}\))
8|n if 8|(the number represented by the last three digits of n)
Examples
Use the divisibility test for 8 to determine if the following is true or false.
1. 8|42,527
This is false because 8 does not divide 527
2. 8|25,336
This is true because 8|336
3. 8|7,624
This is true because 8 does divide 624, (since 8 is a factor of 624)
It should be clear to you that if a number is not divisible by 2, it is not divisible by 4 or 8; and if it is not divisible by 4, it is not divisible by 8. Conversely, if a number is divisible by 8, then it is divisible by both 2 and 4; and if it is divisible by 4, it is divisible by 2.
Exercise 20
Use the divisibility tests for 2, 4 and 8 to determine if the following is true or false. Support your answer with a reason using the appropriate divisibility test.
| a. 2|9,712 _____ |
| b. 2|5,643 _____ |
| c. 4|5,690 _____ |
| d. 4|63,868 _____ |
| e. 4|854,100 _____ |
| f. 8|12,345,248 _____ |
| g. 8| 54,094,422 _____ |
Divisibility Test for 5: 5|n if the last digit of n is 0 or 5
Examples
Use the divisibility test for 5 to determine if the following is true or false.
1. 5|527
This is false because 7 is the last digit of 527
2. 5|25,335
This is true because 5 is the last digit of 25,335
3. 5|7,620
This is true because 0 is the last digit of 7,620
Divisibility Test for 10: 10|n if the last digit of n is 0
Examples
Use the divisibility test for 10 to determine if the following is true or false.
1. 10|527
This is false because 7 is the last digit of 527
2. 10|25,335
This is false because 5 is the last digit of 25,335
3. 10|7,620
This is true because 0 is the last digit of 7,620
Exercise 21
Use the divisibility tests for 5 and 10 to determine if the following is true or false. Support your answer with a reason using the appropriate divisibility test.
| a. 5|9,750 _____ |
| b. 5|5,645 _____ |
| c. 5|5,696 _____ |
| d. 10|63,860 _____ |
| e. 10|854,105 _____ |
Divisibility Test for 3: 3|n if 3|(the digital root of n)
Note: This is equivalent to saying 3|n if the digital root of n is 0, 3 or 6
Examples
Use the divisibility test for 3 to determine if the following is true or false.
1. 3|97
This is false because 3 does not divide 7, which is the digital root of 97
2. 3|356
This is false because 3 does not divide 5, which is the digital root of 356
3. 3|738
This is true because 3|0, where 0 is the digital root of 738
Exercise 22
Use the divisibility test for 3 to determine if the following is true or false. Support your answer with a reason using the divisibility test for 3. Show work.
| a. 3|9,750 ______ |
| b. 3|5,645 ______ |
| c. 3|5,696 ______ |
| d. 3|63,860 ______ |
| e. 3|854,115 ______ |
Divisibility Test for 9: 9|n if 9|(the digital root of n)
Note: This is equivalent to saying that the digital root of n must equal zero. Take a moment to think about this divisibility test for 9. In exercise 16, we discovered that the digital root of a number is the same as the remainder you obtain when you divide a number by 9. In order for a number to be divisible by 9, the remainder would be zero, which is exactly what the digital root would be.
Examples
Use the divisibility test for 9 to determine if the following is true or false.
1. 9|627
This is false because 9 does not divide 6, which is the digital root of 627.
2. 9|25,334
This is false since 9 does not divide 8, which is the digital root of 25,334.
3. 9|7,533
This is true because the digital root of 9 is 0.
Exercise 23
Use the divisibility test for 9 to determine if the following is true or false. Support your answer with a reason using the divisibility test for 9. Show work.
| a. 9|9,753 ______ |
| b. 9|5,646 ______ |
| c. 9|5,697 ______ |
| d. 9|63,576 ______ |
| e. 9|854,103 ______ |
Divisibility Test for 6: 6|n if 2|n AND 3|n. (Think of 6 as \(2 \cdot 3\))
Important Note: A number is divisible by 6 only if it passes the divisibility test for both 2 and 3. If it doesn't pass one of the tests, then it is not divisible by 6. To show it is divisible by 6, you must show it passes both of the tests.
Examples
Use the divisibility test for 6 to determine if the following is true or false.
1. 6|627
This is false because 2 does not divide 7 (the last digit, which is not even).
2. 6|25,334
This is false because 3 does not divide 25,334, since 3 does not divide the digital root, which is 8.
3. 6|7,620
This is true because 2|7,620 (since the last digit, 0, is even) AND 3|7,620 (since 3|6, where 6 is the digital root of 7,620).
Exercise 24
Use the divisibility test for 6 to determine if the following is true or false. Support your answer with a reason using the divisibility test for 6.
| a. 6|9,753 |
| b. 6|5,645 |
| c. 6|5,696 |
| d. 6|63,876 |
| e. 6|854,103 |
Divisibility Test for 15: 15|n if 5|n AND 3|n. (Think of 15 as \(5 \cdot 3\))
Important Note: A number is divisible by 15 only if it passes the divisibility test for both 5 and 3. If it doesn't pass one of the tests, then it is not divisible by 15. To show it is divisible by 15, you must show it passes both of the tests.
Examples
Use the divisibility test for 15 to determine if the following is true or false.
1. 15|623: This is false because 5 does not divide 623 (since the last digit is not 0 or 5).
2. 15|24,335: This is false because 3 does not divide 24,335, since 3 does not divide the digital root, which is 8.
3. 15|7,620: This is true because 5|7,620 (since the last digit is 0) AND 3|7,620 (since 3|6, where 6 is the digital root of 7,620).
Exercise 25
Use the divisibility test for 15 to determine if the following is true or false. Support your answer with a reason using the divisibility test for 15.
| a. 15|9,753 |
| b. 15|6,645 |
| c. 15|5,690 |
| d. 15|63,872 |
| e. 15|654,105 |
Divisibility Test for 7: This test isn't easy to describe. Below are the steps.
Step 1: Cross off the one's digit of the number to get a number with one less place value.
Step 2: Double the one's digit you crossed off and subtract from the new number obtained with the one's digit missing.
Step 3: If 7 divides the number you get after subtracting, it divides the original number. Otherwise, it doesn't. If you aren't sure, repeat the procedure on the new number by going back to step 1.
Examples
Use the divisibility test for 7 to determine if the following is true or false. The way you would show the steps using the numbers is shown to the right of the explanation.
|
1. 7|91: Cross off the 1, double it (2), and subtract from what is left (9). The answer is 7 (9 – 2 = 7). Since 7|7, 7|91 is true. 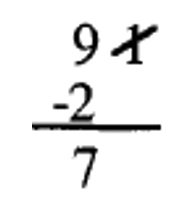 |
|
2. 7|96: Cross off the 6, double it (12), and subtract from what is left (9). When you subtract, ignore the sign (just do 12 – 9 = 3). Since 7 does not divide 3, 7|96 is false. 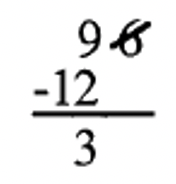 |
|
3. 7|638: Cross off the 8, double it (16) and subtract from what is left (63). The answer is 47 (63 – 16 = 47). Since 7 does not divide 47, then 7|638 is false. (If you weren't sure whether or not 7 divided 47, you can take it a step further; this is shown to the right.) 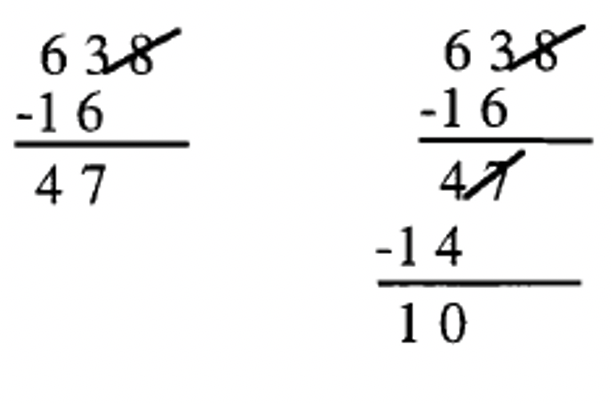 |
|
4. 7|4564: Cross off the 4, double it (8) and subtract from what is left (456). The answer is 448 (456 – 8 = 456). Cross off the 8, double it (16) and subtract from what is left (44). The answer is 28 (44 – 16 = 28). Since 7|28, then 7|4564 is true. 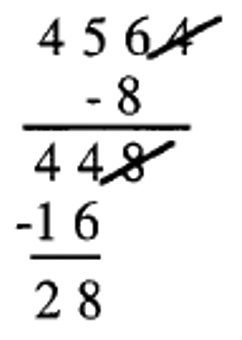 |
|
5. 7|56161: Cross off the 1, double it (2) and subtract from what is left (5616 – 2 = 5614). Cross off the 4, double it (8) and subtract from what is left (561 – 8 = 553). Cross off the 3, double it (6) and subtract from what is left (55 – 6 = 49). Since 7|49, then 7|56161 is true. 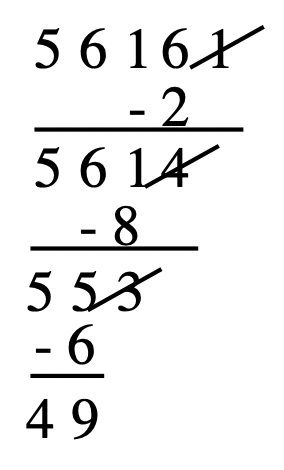 |
Exercise 26
Use the divisibility test for 7 to determine if the following is true or false. Support your answer with a reason using the divisibility test for 7. Show work.
| a. 7|833 |
| b. 7|5,645 |
| c. 7|4,795 |
| d. 7|14,763 |
Divisibility Test for 11: 11|n if the difference between the sum of the digits in the places that are even powers of 10 and the sum of the digits in the places that are odd powers of 10 is divisible by 11.
This test is more confusing to describe than to do. What you do is add up every other digit. Then, add up the ones you skipped. Then, subtract these two numbers and see if 11 divides this number.
Examples
Use the divisibility test for 11 to determine if the following is true or false.
a. 11|4,365: Add 4 + 6 = 10 Add 3 + 5 = 8 Subtract 10 – 8 = 2 Since 11 doesn't divide 2, then 11 doesn't divide 4365. Therefore, 11|4365 is false.
b. 11|540,879,216: Add 5 + 0 + 7 + 2 + 6 = 20. Add 4 + 8 + 9 + 1 = 22. Subtract 22 – 20 = 2 Since 11 doesn't divide 2, 11|540,879,216 is false.
c. 11|542,879,216: Add 5 + 2 + 7 + 2 + 6 = 22 Add 4 + 8 + 9 + 1 = 22 Subtract 22 – 22 = 0 Since 11|0, then 11|542,879,216 is true.
d. 11|4,052,631: Add 4 + 5 + 6 + 1 = 16 Add 0 + 2 + 3 = 5 Subtract 16 – 5 = 11 Since 11|11, then 11|4,052,631 is true.
Exercise 27
Use the divisibility test for 11 to determine if the following is true or false. Support your answer with a reason using the divisibility test for 11. Show work.
| a. 11|9,053 |
| b. 11|63,920,876 |
| c. 11|568,696 |
| d. 11|513,645 |
| e. 11|803,003,808 |
Listed below are the divisibility tests that you should know. It's important to realize that each of the tests only work for the number specified. In other words, you can't use the divisibility test for 3 to determine is 7 divides a number. The divisibility test for 7 has nothing to do with digital roots!
Divisibility Test for 2: 2|n if the last digit of n is even (0, 2, 4, 6, or 8)
Divisibility Test for 3: 3|n if 3|(the digital root of n); OR 3|n if the digital root of n is 0, 3 or 6
Divisibility Test for 4: 4|n if 4|(the number represented by the last two digits of n)
Divisibility Test for 5: 5|n if the last digit of n is 0 or 5
Divisibility Test for 6: 6|n if 2|n AND 3|n. (Think of 6 as \(2 \cdot 3\))
Divisibility Test for 7: The steps of this test are described below.
- Step 1: Cross off the one's digit of the number to get a number with one less place value.
- Step 2: Double the one's digit you crossed off and subtract from the new number without the one's digit.
- Step 3: If 7 divides the number you get after subtracting, it divides the original number. Otherwise, it doesn't. If you aren't sure, repeat the procedure on the new number by going back to step 1.
Divisibility Test for 8: 8|n if 8|(the number represented by the last three digits of n)
Divisibility Test for 9: 9|n if 9|(the digital root of n); OR 9|n if the digital root of n is zero
Divisibility Test for 10: 10|n if the last digit of n is 0
Divisibility Test for 11: 11|n if the difference between the sum of the digits in the places that are even powers of 10 and the sum of the digits in the places that are odd powers of 10 is divisible by 11
Divisibility Test for 15: 15|n if 5|n AND 3|n


