3.8: Algebra and Composition of Functions

Learning Objectives

• Create new functions using algebraic operations.
• Evaluate combined algebraic functions.
• Find the domain of combined algebraic functions.
• Create new functions by composition of functions.
• Evaluate composite functions.
• Describe what composite functions represent in real-life situations.
• Find the domain of composite functions.
• Decompose a composite function into its component functions.

Are You Ready?

Try these questions prior to beginning this section to help determine if you are set up for success:

1. Simplify:
   1. \(\quad \dfrac{m}{m+2}+5-\dfrac{8}{m^2-4}\)
   2. \(\quad (\sqrt{2t+1}-3)^2\)
2. Solve:
   1. \(\quad \sqrt{5x}=2+\sqrt{x+4}\)
   2. \(\quad \dfrac{4}{2h^2-7h-15}=\dfrac{2}{2h^2+13h+15}-\dfrac{2}{h^2-25}\)

Answer

1. 1. \(\quad \dfrac{2(3m-7)}{m-2}\), If you missed this problem or feel you could use more practice, review [2.14: Adding and Subtracting Rational Expressions]
   2. \(\quad 2t+10-6\sqrt{2t+1}\), If you missed this problem or feel you could use more practice, review [2.20: Adding, Subtracting, and Multiplying Radical Expressions]
2. 1. \(\quad x=5\), If you missed this problem or feel you could use more practice, review [2.22: Solving Radical Equations]
   2. \(\quad h=-6\), If you missed this problem or feel you could use more practice, review [2.16: Solving Rational Equations]

Suppose we want to calculate how much it costs to heat a house on a particular day of the year. The cost to heat a house will depend on the average daily temperature, and in turn, the average daily temperature depends on the particular day of the year. Notice how we have just defined two relationships: The cost depends on the temperature, and the temperature depends on the day.

Using descriptive variables, we can notate these two functions. The function \(C(T)\) gives the cost \(C\) of heating a house for a given average daily temperature in \(T\) degrees Celsius. The function \(T(d)\) gives the average daily temperature on day d of the year. For any given day, \(Cost=C(T(d))\) means that the cost depends on the temperature, which in turns depends on the day of the year. Thus, we can evaluate the cost function at the temperature \(T(d)\). For example, we could evaluate \(T(5)\) to determine the average daily temperature on the 5th day of the year. Then, we could evaluate the cost function at that temperature. We would write \(C(T(5))\).

Figure \(\PageIndex{1}\): Explanation of \(C(T(5))\), which is the cost for the temperature and \(T(5)\) is the temperature on day 5.

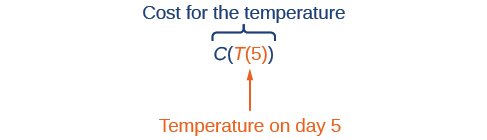
By combining these two relationships into one function, we have performed function composition, which is one way to combine functions together to form new functions.

Combining Functions Using Algebraic Operations

Function composition is only one way to combine existing functions. Another way is to carry out the usual algebraic operations on functions, such as addition, subtraction, multiplication and division. We do this by performing the operations with the function outputs, defining the result as the output of our new function.

Suppose we need to add two columns of numbers that represent a husband and wife’s separate annual incomes over a period of years, with the result being their total household income. We want to do this for every year, adding only that year’s incomes and then collecting all the data in a new column. If \(w(y)\) is the wife’s income and \(h(y)\) is the husband’s income in year \(y\), and we want \(T\) to represent the total income, then we can define a new function.

\[T(y)=h(y)+w(y) \nonumber\]

If this holds true for every year, then we can focus on the relation between the functions without reference to a year and write

\[T=h+w \nonumber\]

We can define other algebraic operations with functions in a similar way.

Algebra of Functions

For two functions \(f(x)\) and \(g(x)\) where \(x\) is in the domain of both \(f\) and \(g\), we define new functions \(f+g\), \(f−g\), \(fg\), and \(\frac{f}{g}\) by the relations:

\[ \begin{align*} (f+g)(x) &=f(x)+g(x) \\[5pt] (f−g)(x) &=f(x)−g(x) \\[5pt] (fg)(x)&=f(x)g(x) \\[5pt] \left(\dfrac{f}{g}\right)(x) &=\dfrac{f(x)}{g(x)}, g(x)\neq{0} \end{align*}\]

Example \(\PageIndex{1}\)

Given \(f(x)=x−1\) and \(g(x)=x^2−1\). find and simplify the functions \((g−f)(x)\) and \(\left(\dfrac{g}{f}\right)(x)\).

Solution

Begin by writing the general form, and then substitute in the given functions.

\[\begin{align*} (g−f)(x) &= g(x)−f(x) \\[4pt]  &=x^2−1−(x−1) \\[4pt] &=x^2−x \\[4pt] &=x(x−1) \end{align*}\]

\[\begin{align*} \left(\dfrac{g}{f}\right)(x)&=\dfrac{g(x)}{f(x)} \\[4pt] &=\dfrac{x^2−1}{x−1} \\[4pt] &=\dfrac{(x+1)(x−1)}{x−1} \\[4pt]&=x+1, x\neq{1} \end{align*}\]

Note: For \(\left(\dfrac{g}{f}\right)(x)\), the condition \(x\neq1\) must be stated after simplifying. Remember that function operations can only be performed for all \(x\)-values in the domain of both \(f\) and \(g\) where \(g(x)\neq{0}\) which was assumed when we simplified.

Caution!

Remember to state domain restrictions for functions formed using algebra of functions. If the domain restriction is not visually apparent after simplifying, as in the previous example, it must be stated for the combined function to be correct.

You Try \(\PageIndex{1}\)

Given \(f(x)=x−1 \text{ and } g(x)=x^2−1 \), find and simplify the functions \((fg)(x)\) and \((f−g)(x)\).

Answer

\((fg)(x)=f(x)g(x)=(x−1)(x^2−1)=x^3−x^2−x+1 \\[4pt] (f−g)(x)=f(x)−g(x)=(x−1)−(x^2−1)=x−x^2\)

When performing function operations, make sure to use correct notation by including parentheses around each function so that operations are performed correctly.

In the previous example, it would be incorrect to write

\((fg)(x)=f(x)g(x)=x−1*x^2−1\) since this simplifies to \(x-x^2-1\)

Similarly, it would be incorrect to write

\((f−g)(x)=f(x)−g(x)=x−1−x^2−1\) since this simplifies to \(-x^2+x-2\)

Caution!

Using correct mathematical notation is important. When performing operations with multiple terms, use parentheses. Provided below are some examples of notations that are not equivalent.

\[(x+2)(x-5)\neq x+2*x-5\nonumber \]

\[(x+2)-(x-5)\neq x+2-x-5\nonumber \]

Evaluating Functions Formed Algebraically From Two Functions

Just like with any function we can evaluate functions that were combined algebraically. Let's look at an example.

Example \(\PageIndex{2}\)

Let \(f(x) = 6x^2 - 2x\) and \(g(x) = 3-\dfrac{1}{x}\).

1. Find \((f+g)(-1)\)
2. Find \((fg)(2)\)

Solution

1. To find \((f+g)(-1)\) we first find \(f(-1) = 8\) and \(g(-1) = 4\). By definition, we have that \[\begin{align*}(f+g)(-1) &= f(-1) + g(-1) \\&= 8+4 \\&= 12\end{align*}\]
2. To find \((fg)(2)\), we first need \(f(2)\) and \(g(2)\). Since \(f(2) = 20\) and \(g(2) = \frac{5}{2}\), our formula yields \[\begin{align*}((fg)(2) &= f(2) g(2) \\&= (20)\left(\frac{5}{2}\right) \\&= 50\end{align*}\]

Note that you can also find the formula for the combined function first, then evaluate. You will get the same result as above.

Finding Domain of a Function Formed Algebraically From Two Functions

Remember that to combine two functions algebraically, \(f\) and \(g\), that the input values must be in the domain of both functions. Let's look at an example of finding domain.

Example \(\PageIndex{3}\)

Let \(f(x) = 6x^2 - 2x\) and \(g(x) = 3-\dfrac{1}{x}\).

1. Find the domain of \(g-f\) then find and simplify \((g-f)(x)\).
2. Find the domain of \(\left(\frac{g}{f}\right)\) then find and simplify \(\left(\frac{g}{f}\right)(x)\).

Solution

1. To find the domain of \(g-f\), find the domain of \(g\) and of \(f\) separately, then find the intersection of these two sets. The domain of \(g\) is \((-\infty, 0) \cup (0, \infty)\). The domain of \(f\) is \((-\infty, \infty)\). Thus the domain of \(g-f\) is \((-\infty, 0) \cup (0, \infty)\).

   Moving along, we need to simplify \((g-f)(x)\).

   \[ \begin{array}{rclr} (g-f)(x) & = & g(x) - f(x) & \\ & = & \left(3-\dfrac{1}{x}\right) - \left(6x^2 - 2x\right) &\\ & = & 3 - \dfrac{1}{x} - 6x^2 + 2x & \\ & = & \dfrac{3x}{x} - \dfrac{1}{x} - \dfrac{6x^3}{x} + \dfrac{2x^2}{x} & \\ & = & \dfrac{3x - 1 - 6x^3 + 2x^2}{x} & \\ & = & \dfrac{-6x^3+2x^2+3x-1}{x} \text{, }\: x\neq0 & \\ \end{array}\nonumber\]

2. To find the domain of \(\frac{g}{f}\), first find the domain of \(g\) and \(f\) separately and then find the intersection of these two sets. Also, since \(\left(\frac{g}{f}\right)(x) = \frac{g(x)}{f(x)}\), we are introducing a new denominator, namely \(f(x)\) in this case, we need to guard against this being \(0\). Our previous work tells us that the domain of \(g\) is \((-\infty, 0) \cup (0, \infty)\) and the domain of \(f\) is \((-\infty, \infty)\). Setting \(f(x) = 0\) gives \(6x^2 - 2x = 0\) or \(x = 0, \frac{1}{3}\). As a result, the domain of \(\frac{g}{f}\) is all real numbers except \(x = 0\) and \(x = \frac{1}{3}\), or \((-\infty, 0) \cup \left(0, \frac{1}{3} \right) \cup \left( \frac{1}{3}, \infty \right)\).

Next, we find and simplify \(\left(\dfrac{g}{f}\right)(x)\). \[\begin{align*}\left(\frac{g}{f}\right)(x) &=\dfrac{g(x)}{f(x)}\\[5pt] &= \dfrac{3-\dfrac{1}{x}}{6x^2-2x}\\[5pt] &=\dfrac{x}{x} \cdot \dfrac{3-\dfrac{1}{x}}{6x^2-2x}\\[5pt] &=\dfrac{x\cdot \left(3-\dfrac{1}{x}\right)}{x\cdot(6x^2-2x)}\\[5pt] &=\dfrac{3x-1}{2x^2\cdot(3x-1)}\\[5pt] &=\dfrac{1}{2x^2} \text{, }\: x\neq0,\dfrac{1}{3} \end{align*}\]

Hence, \(\left(\dfrac{g}{f}\right)(x)=\frac{1}{2x^2}, x\neq0, \frac{1}{3}\)

Note the importance of finding the domain of a function \(\textit{before}\) simplifying its expression. In part 2 in the previous example, had we waited to find the domain of \(\frac{g}{f}\) until after simplifying, we'd just have the formula \(\frac{1}{2x^2}\) to go by, and we would (incorrectly!) state the domain as \((-\infty, 0) \cup (0,\infty)\), since the other troublesome number, \(x = \frac{1}{3}\), was canceled away.

Example \(\PageIndex{4}\)

Given \(h(x)=\dfrac{x}{3x-2}\), \(l(x)=\dfrac{x}{2x+3}\), and \(m(x)=\dfrac{x+4}{6x^2+5x-6}\),

1. Find and simplify \((h-l)(x)\).
2. What is the domain of \(h-l\)? State your answer in interval notation.
3. For what x-values does \((h-l)(x)=m(x)\)?

Solution

1. \[\begin{align*} (h-l)(x)&=\dfrac{x}{3x-2}-\dfrac{x}{2x+3}\\[6pt] &=\dfrac{x(2x+3)-x(3x-2)}{(3x-2)(2x+3)}\\[6pt] &=\dfrac{2x^2+3x-3x^2+2x}{(3x-2)(2x+3)}\\[6pt] &=\dfrac{-x^2+5x}{(3x-2)(2x+3)}\\[6pt] ​\end{align*}\]
2. The domain of \(h-l\) is \(\left(-\infty, -\dfrac{3}{2}\right)\cup \left(-\dfrac{3}{2},\dfrac{2}{3}\right) \cup \left(\dfrac{2}{3},\infty\right)\).
3. You may choose to work with simplified version of \(h-l\) that was found in part 1 or the original functions, h and l, when solving. The simplified function found in part 1 was used for solving in the following steps. \[\begin{align*} (h-l)(x)&=m(x)\\[4pt] \dfrac{-x^2+5x}{(3x-2)(2x+3)}&=\dfrac{x+4}{6x^2+5x-6}\\[4pt] \dfrac{-x^2+5x}{(3x-2)(2x+3)}&=\dfrac{x+4}{(3x-2)(2x+3)}\\[4pt]\end{align*}\]

   Multiplying both sides by the common denominator,\((3x-2)(2x+3)\), we get \[\begin{align*} -x^2+5x&=x+4\\[4pt] -x^2+4x-4&=0\\[4pt] x^2-4x+4&=0\\[4pt] (x-2)^2&=0\\[4pt] x&=2\end{align*}\]

   Verifying that this is not an extraneous solution, we can conclude that \((h+l)(x)=m(x)\) at \(x=2\).

   Remember that solutions to equations relate to where graphs of functions intersect. If we want to know the point where the graph of \(h+l\) intersects \(m\), we can evaluate both functions at \(x=2\):

   \[\begin{array}{l} {(h-l)(2)=\dfrac{-(2)^2+5(2)}{(3(2)-2)(2(2)+3)}}\\[6pt] {(h-l)(2)=\dfrac{3}{14}}\end{array} \qquad \text{ and } \qquad \begin{array}{l} {m(2)=\dfrac{(2)+4}{6(2)^2+5(2)-6}}\\[6pt]{m(2)=\dfrac{3}{14}}\end{array} \nonumber\]The point where \((h-l)(x)\) intersects \(m(x)\) is at \(\left(2,\frac{3}{14}\right)\).

   Looking at the graph of \(h-l\) and \(m\), denoted by blue and red graphs respectively, it is difficult to see this point where the graphs intersect.

   

   Figure \(\PageIndex{2}\): Graphs of (h-l)(x) and m(x)

   If you try different windows for viewing the graphs of these two functions you will find that in almost all windows it will be very difficult to clearly see the point of intersection. This is just one of many examples that illustrates the importance of why we need to have good algebra skills so we can apply them in situations such as this. In addition, understanding the behavior of functions helps us to better have an intuitive sense of the types of solutions we might expect when solving equations.

You Try \(\PageIndex{2}\)

Given \(A(t)=\sqrt{7t+4} \text{ and } B(t)=\sqrt{t+1}\), where does \((A-B)(t)=3\)?

Answer

\((A-B)(t)=3 \text{ at } t=3\).

Note that \(t=0\) is extraneous. Upon viewing the graph of \(A-B\) with the line \(y=3\) we can see that the graphs intersect at \(t=3\), as seen below in Figure \(\PageIndex{3}\).

Figure \(\PageIndex{3}\): Graphs of (A-B)(x) and y=3 showing the point (3,3) where they intersect

Composition of Functions

Earlier, we discussed wanting to compute a heating cost from a day of the year. To do this we created a new function that takes a day as input and yields a cost as output. This process of combining functions so that the output of one function becomes the input of another is known as composition of functions. The resulting function is known as a composite function. We represent this combination by the following notation:

\[(f\:{\circ}\:g)(x)=f(g(x))\nonumber\]

We read the left-hand side as“\(f\) composed with \(g\) at \(x\),” and the right-hand side as“\(f\) of \(g\) of \(x\).” The two sides of the equation have the same mathematical meaning and are equal. The open circle symbol \(\circ\) is called the composition operator. It is important not to confuse function composition with multiplication because they are different operations.

It is also important to understand the order of operations in evaluating a composite function. We follow the usual order of operations convention with parentheses by starting with the innermost parentheses first, and then working to the outside. To perform composition, \((f\:{\circ}\:g)(x)=f(g(x))\), the function \(g\) takes the input \(x\) first and yields an output \(g(x)\). Then the function \(f\) takes \(g(x)\) as an input and yields an output \(f(g(x))\).

Figure \(\PageIndex{4}\): Explanation of the composite function.

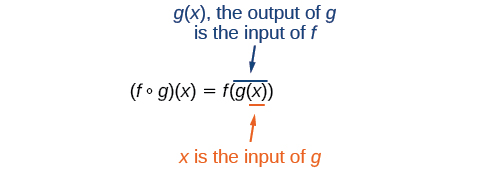
In general, \(f\:{\circ}\:g\) and \(g\:{\circ}\:f\) are different functions. In other words, in many cases \(f(g(x)){\neq}g(f(x))\) for all \(x\). We will also see that sometimes two functions can be composed only in one specific order.

For example, if \(f(x)=x^2\) and \(g(x)=x+2\), then

\[\begin{align*} f(g(x))&= f(x+2) \\[4pt]&=(x+2)^2 \\[4pt] &=x^2+4x+4 \end{align*}\]

but

\[\begin{align*} g(f(x))&= g(x^2) \\[4pt]&=x^2+2 \end{align*}\]

These expressions are not equal for all values of x, so the two functions are not equal.

Note that the range of the inside function (the first function to be evaluated) needs to be within the domain of the outside function. Less formally, the composition has to make sense in terms of inputs and outputs.

Composition of Functions

When the output of one function is used as the input of another, we call the entire operation a composition of functions. The composition of functions \(f\) and \(g\), defined as \(f\:{\circ}\:g\), is called composite function such that

\[(f\:{\circ}\:g)(x)=f(g(x))\nonumber\]

The domain of the composite function \(f\:{\circ}\:g\) is all \(x\) such that \(x\) is in the domain of \(g\) and \(g(x)\) is in the domain of \(f\).

Remember: It is important to realize that the product of functions \(fg\) is not the same as the function composition \(f(g(x))\), because, in general, \(f(x)g(x){\neq}f(g(x))\).

Example \(\PageIndex{5}\)

Using the functions provided, find \((f\:{\circ}\:g)(x)\) and \((g\:{\circ}\:f)(x)\).

\[f(x)=2x+1 \;\;\;\; g(x)=3−x \nonumber\]

Solution

Let’s begin by substituting \(g(x)\) into \(f(x)\).

\[\begin{align*} (f\:{\circ}\:g)(x) &= f(g(x)) \\[4pt] &= 2(3−x)+1 \\[4pt] &=6−2x+1 \\[4pt] &=7−2x \end{align*}\]

Now we can substitute \(f(x)\) into \(g(x)\).

\[\begin{align*} (g\:{\circ}\:f)(x)&=g(f(x))\\[4pt]&= 3−(2x+1) \\[4pt]&=3−2x−1 \\[4pt] &=2-2x \end{align*}\]

Note that \((f\:{\circ}\:g)(x){\neq}(g\:{\circ}\:f)(x)\).

Evaluating Composite Functions

Next, let's look at an example of evaluating composite functions.

Example \(\PageIndex{6}\)

Given \(f(t)=t^2−t\) and \(h(x)=3x+2\), evaluate \((f\:{\circ}\:h)(1)\).

Solution

Because the inside expression is \(h(1)\), we start by evaluating \(h(x)\) at 1.

\[ \begin{align*} h(1)&=3(1)+2 \\[4pt] h(1)&=5 \end{align*} \]

Then \(f(h(1))=f(5)\), so we evaluate \(f(t)\) at an input of 5.

\[ \begin{align*} (f\:{\circ}\:h)(1)&=f(h(1)) \\[5pt] &=f(5) \\[5pt] &=5^2−5 \\[5pt] &=20 \end{align*} \]

Note that it makes no difference what the input variables \(t\) and \(x\) were called in this problem because we evaluated for specific numerical values.

You could also find the formula for the composite function, \(f\:{\circ}\:h\), then evaluate. You will get the same result as above.

You Try \(\PageIndex{3}\)

Given \(f(t)=t^2−t\) and \(h(x)=3x+2\), evaluate

a. \((h\:{\circ}\:f)(2)\)
b. \((h\:{\circ}\:f)(-2)\)

Answer a

8

Answer b

20

When working with functions given as tables, we read input and output values from the table entries and always work from the inside to the outside. We evaluate the inside function first and then use the output of the inside function as the input to the outside function.

Example \(\PageIndex{7}\)

Using the tables below, evaluate \((f\:{\circ}\:g)(3)\) and \((g\:{\circ}\:f)(4) \)

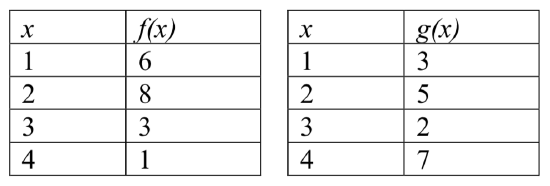
Solution

To evaluate \((f\:{\circ}\:g)(3)\), we start from the inside with the value 3. We then evaluate the inside expression \(g(3)\) using the table that defines the function \(g: g(3) = 2\).

We can then use that result as the input to the \(f\) function, so \(g(3)\) is replaced by the equivalent value 2 and we can evaluate \(f(2)\). Then using the table that defines the function \(f\), we find that \(f(2) = 8\).

\[(f\:{\circ}\:g)(3)=f(2)=8. \nonumber\]

To evaluate \((g\:{\circ}\:f)(4)\), we first evaluate the inside expression \(f(4)\)using the first table: \(f(4) = 1\). Then using the table for \(g\) we can evaluate:

\[(g\:{\circ}\:f)(4)=g(1)=3. \nonumber\]

You Try \(\PageIndex{4}\)

Using the tables from the example above, evaluate \((f\:{\circ}\:g)(1)\) and \((g\:{\circ}\:f)(3) \).

Answer

\((f\:{\circ}\:g)(1) = f(3) = 3\) and \((g\:{\circ}\:f)(3) = g(3) = 2\)

When we are given individual functions as graphs, the procedure for evaluating composite functions is similar to the process we use for evaluating tables. We read the input and output values, but this time, from the x- and y-axes of the graphs.

Example \(\PageIndex{8}\)

Using Figure \(\PageIndex{5}\), evaluate \((f\:{\circ}\:g)(1)\).

Solution

To evaluate \((f\:{\circ}\:g)(1)\), we start with the inside evaluation. See Figure \(\PageIndex{5}\).

Figure \(\PageIndex{5}\): Two graphs of parabolas, one that opens upward, \(g(x)\), and one that opens downward, \(f(x)\). The following points are plotted: \(g(1)=3\) and \(f(3)=6\).

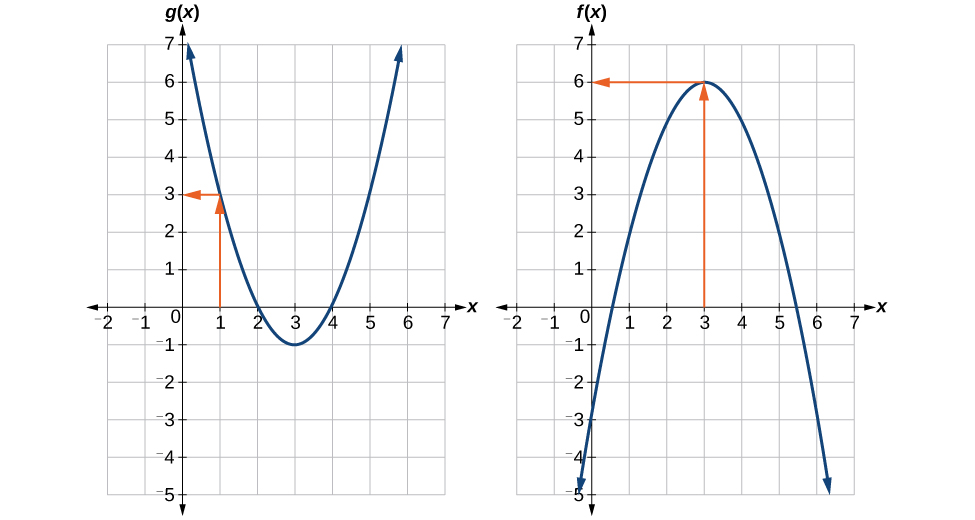
We evaluate \(g(1)\) using the graph of \(g(x)\), finding the input of 1 on the x-axis and finding the output value of the graph at that input. Here, \(g(1)=3\). We use this value as the input to the function \(f\).

\[(f\:{\circ}\:g)(1)=f(3) \nonumber\]

We can then evaluate the composite function by looking to the graph of \(f(x)\), finding the input of 3 on the x-axis and reading the output value of the graph at this input. Here, \(f(3)=6\), so \((f\:{\circ}\:g)(1)=6\).

You Try \(\PageIndex{5}\)

Using Figure \(\PageIndex{5}\) in the previous example, evaluate \((g\:{\circ}\:f)(5) \).

Answer

\((g\:{\circ}\:f)(5)=g(2)=0\)

Interpretation of Composite Functions

There are many real-life situations that can be modeled using composite functions. It is important that we understand how to combine functions appropriately so that the resulting composite function makes sense. Let's take a look.

Example \(\PageIndex{9}\)

The function \(c(s)\) gives the number of calories burned completing \(s\) sit-ups, and \(s(t)\) gives the number of sit-ups a person can complete in \(t\) minutes. Interpret \((c\:\:{\circ}\:\:s)(3)\).

Solution

The inside expression in the composition is \(s(3)\). Because the input to the \(s\)-function is time, \(t=3\) represents 3 minutes, and \(s(3)\) is the number of sit-ups completed in 3 minutes.

Using \(s(3)\) as the input to the function \(c(s)\) gives us the number of calories burned during the number of sit-ups that can be completed in 3 minutes, or simply the number of calories burned in 3 minutes (by doing sit-ups).

Example \(\PageIndex{10}\)

Suppose \(f(x)\) gives miles that can be driven in \(x\) hours and \(g(y)\) gives the gallons of gas used in driving \(y\) miles. Which of these expressions is meaningful: \(f(g(y))\) or \(g(f(x))\)?

Solution

The function \(y=f(x)\) is a function whose output is the number of miles driven corresponding to the number of hours driven.

\[\text{number of miles } =f (\text{number of hours}) \nonumber\]

The function \(g(y)\) is a function whose output is the number of gallons used corresponding to the number of miles driven. This means:

\[\text{number of gallons } =g(\text{number of miles}) \nonumber\]

The expression \(g(y)\) takes miles as the input and a number of gallons as the output. The function \(f(x)\) requires a number of hours as the input. Trying to input a number of gallons does not make sense. The expression \(f(g(y))\) is meaningless.

The expression \(f(x)\) takes hours as input and a number of miles driven as the output. The function \(g(y)\) requires a number of miles as the input. Using \(f(x)\) (miles driven) as an input value for \(g(y)\), where gallons of gas depends on miles driven, does make sense. The expression \(g(f(x))\) makes sense, and will yield the number of gallons of gas used, \(g\), driving a certain number of miles, \(f(x)\), in \(x\) hours.

You Try \(\PageIndex{6}\)

The gravitational force on a planet a distance \(r\) from the sun is given by the function \(G(r)\). The acceleration of a planet subjected to any force \(F\) is given by the function \(a(F)\). Form a meaningful composition of these two functions, and explain what it means.

Answer

A gravitational force is still a force, so \(a(G(r))\) makes sense as the acceleration of a planet at a distance \(r\) from the Sun (due to gravity), but \(G(a(F))\) does not make sense.

Finding the Domain of a Composite Function

As we discussed previously, the domain of a composite function such as \(f\:{\circ}\:g\) is dependent on the domain of \(g\) and the domain of \(f\). It is important to know when we can apply a composite function and when we cannot, that is, to know the domain of a function such as \(f\:{\circ}\:g\). Let us assume we know the domains of the functions \(f\) and \(g\) separately. If we write the composite function for an input \(x\) as \(f(g(x))\), we can see right away that \(x\) must be a member of the domain of g in order for the expression to be meaningful, because otherwise we cannot complete the inner function evaluation. However, we also see that \(g(x)\) must be a member of the domain of \(f\), otherwise the second function evaluation in \(f(g(x))\) cannot be completed, and the expression is still undefined. Thus the domain of \(f\:{\circ}\:g\) consists of only those inputs in the domain of \(g\) that produce outputs from \(g\) belonging to the domain of \(f\). Note that the domain of \(f\) composed with \(g\) is the set of all \(x\) such that \(x\) is in the domain of \(g\) and g(x)\) is in the domain of \(f\).

Domain of a Composite Function

The domain of a composite function \(f\:{\circ}\:g\) is the set of all inputs \(x\) in the domain of \(g\) for which \(g(x)\) is in the domain of \(f\).

Example \(\PageIndex{11}\)

Find the domain of

\[(f∘g)(x) \text{ where } f(x)=\dfrac{5}{x−1} \text{ and } g(x)=\dfrac{4}{3x−2} \nonumber\]

Solution

The domain of \(g(x)\) consists of all real numbers except \(x=\frac{2}{3}\), since that input value would cause us to divide by 0. Likewise, the domain of \(f\) consists of all real numbers except 1. So we need to exclude from the domain of \(g(x)\) that value of \(x\) for which \(g(x)=1\).

\[\begin{align*} \dfrac{4}{3x-2}&= 1 \\[4pt] 4 &=3x-2 \\[4pt] 6&=3x \\[4pt] x&= 2 \end{align*}\]

So the domain of \(f\:{\circ}\:g\) is the set of all real numbers except \(\frac{2}{3}\) and \(2\). This means that

\[x{\neq} \dfrac{2}{3} \text{ or } x\neq2 \nonumber\]

We can write this in interval notation as

\[\left(−\infty,\dfrac{2}{3}\right)\cup \left(\dfrac{2}{3},2 \right)\cup \left(2,\infty \right) \nonumber\]

Example \(\PageIndex{12}\)

Find the domain of

\[(f\:{\circ}\:g)(x) \text{ where } f(x)=\sqrt{x+2} \text{ and } g(x)=\sqrt{3−x} \nonumber\]

Solution

Because we cannot take the square root of a negative number, the domain of \(g\) is \(\left(−\infty,3\right]\). Now we check the domain of the composite function

\[(f\:{\circ}\:g)(x)=\sqrt{\sqrt{3−x}+2} \nonumber\]

For \((f∘g)(x)=\sqrt{ \sqrt{3−x}+2},\sqrt{3−x}+2≥0,\) since the radicand of a square root must be non-negative. Since square roots are positive, \(\sqrt{3−x}≥0\), or, \(3−x≥0,\) which gives a domain of \((-∞,3]\).

Analysis

This example shows that knowledge of the range of functions (specifically the inner function) can also be helpful in finding the domain of a composite function. It also shows that the domain of \(f\:{\circ}\:g\) can contain values that are not in the domain of \(f\), though they must be in the domain of \(g\).

You Try \(\PageIndex{7}\)

Find the domain of

\[(f\:{\circ}\:g)(x) \text{ where } f(x)=\dfrac{1}{x−2} \text{ and } g(x)=\sqrt{x+4} \nonumber\]

Answer

\([−4,0)∪(0,∞)\)

Decomposing a Composite Function into its Component Functions

In some cases, it is necessary to decompose a complicated function. In other words, we can write it as a composition of two simpler functions. There may be more than one way to decompose a composite function, so we may choose the decomposition that appears to be most expedient.

Example \(\PageIndex{13}\)

Write \(f(x)=\sqrt{5−x^2}\) as the composition of two functions.

Solution

We are looking for two functions, \(g\) and \(h\), so \(f(x)=g(h(x))\). To do this, we look for a function inside a function in the formula for \(f(x)\). As one possibility, we might notice that the expression \(5−x^2\) is the inside of the square root. We could then decompose the function as

\[h(x)=5−x^2 \text{ and } g(x)=\sqrt{x} \nonumber\]

We can check our answer by recomposing the functions.

\[g(h(x))=g(5−x^2)=\sqrt{5−x^2} \nonumber\]

You Try \(\PageIndex{8}\)

Write \(f(x)=\dfrac{4}{3−\sqrt{4+x^2}}\) as the composition of two functions.

Answer

There are multiple possible answers. Here's one:

\(g(x)=\sqrt{4+x^2}\)

\(h(x)=\dfrac{4}{3−x}\)

\(f=h\:{\circ}\:g\)

Contributors and Attributions

• Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.