4.6: Introduction to Rational Functions
- Page ID
- 89422
- Find asymptotes of rational functions.
- Find holes of rational functions.
- Describe behavior of graph near asymptotes.
- Describe end behavior of rational functions.
If we add, subtract, or multiply polynomial functions, we will produce another polynomial function. If, on the other hand, we divide two polynomial functions, the result may not be a polynomial. Division of polynomials gives us another important family of functions, called rational functions.
A rational function is a function which is the ratio of polynomial functions of the form
\[ r(x) = \dfrac{p(x)}{q(x)} \nonumber \]
where \(p\) and \(q\) are polynomial function and \(q(x) \neq 0\).
Recall that we have domain issues any time the denominator of a fraction is zero. In the example below, we review this concept as well as some of the algebra of rational expressions.
Find the domain of the following rational functions. Write them in the form \(\dfrac{p(x)}{q(x)}\) for polynomial functions \(p\) and \(q\) and simplify.
- \(f(x) = \dfrac{2x-1}{x+1}\)
- \(g(x) = 2 - \dfrac{3}{x+1}\)
- \(h(x) = \dfrac{2x^2-1}{x^2-1} - \dfrac{3x-2}{x^2-1}\)
- \(r(x) = \dfrac{2x^2-1}{x^2-1} \div \dfrac{3x-2}{x^2-1}\)
Solution
1. We find the zeros of the denominator and exclude them from the domain. Setting \(x+1=0\) results in \(x=-1\). The domain is \((-\infty, -1) \cup (-1,\infty)\). The function \(f(x)\) is already in simplest form since there are no common factors among the numerator and denominator.
2. We determine the domain of \(g\) by solving \(x+1=0\). The domain of \(g\) is \((-\infty, -1) \cup (-1,\infty)\). To simplify \(g(x)\), we need to get a common denominator
\[ \begin{align*} g(x) &= 2 - \dfrac{3}{x+1} \\[5pt] & = \dfrac{2}{1} - \dfrac{3}{x+1} \\[5pt]& = \dfrac{(2)(x+1)}{(1)(x+1)} - \dfrac{3}{x+1} \\[5pt]& = \dfrac{(2x+2) - 3}{x+1}\\[5pt] & = \dfrac{2x-1}{x+1} \end{align*} \nonumber\]
3. The denominators for \(h(x)\) are both \(x^2-1\) whose zeros are \(x = \pm 1\). The domain of \(h\) is \((-\infty, -1) \cup (-1,1) \cup (1, \infty)\). Since we have the same denominator in both terms, we subtract the numerators. We then factor the resulting numerator and denominator, and cancel out the common factor.
\[ \begin{align*} h(x) & = \dfrac{2x^2-1}{x^2-1} - \dfrac{3x-2}{x^2-1} \\[5pt] & =\dfrac{\left(2x^2-1\right) - \left(3x-2\right)}{x^2-1} \\[5pt] & =\dfrac{2x^2-1 - 3x+2}{x^2-1}\\[5pt] & = \dfrac{2x^2 - 3x+1}{x^2-1} \\[5pt] & = \dfrac{(2x-1)(x-1)}{(x+1)(x-1)}\\[5pt] & = \dfrac{2x-1}{x+1} & & \\ \end{align*} \nonumber\]
4. To find the domain of \(r\), it may help to temporarily rewrite \(r(x)\) as
\[ r(x) = \dfrac{\dfrac{2x^2-1}{x^2-1} }{\dfrac{3x-2}{x^2-1}\vphantom{\left(\dfrac{X}{X}\right)}}\nonumber \]
We need to set all of the denominators equal to zero which means we need to solve not only \(x^2-1= 0\), but also \(\dfrac{3x-2}{x^2-1}=0\). We find \(x = \pm 1\) for the former and \(x= \dfrac{2}{3}\) for the latter. The domain is \((-\infty, -1) \cup \left(-1,\dfrac{2}{3}\right) \cup \left(\dfrac{2}{3},1\right) \cup (1, \infty)\). We simplify \(r(x)\) by rewriting the division as multiplication by the reciprocal and then by canceling the common factor
\[ \begin{align*}r(x) & = \dfrac{2x^2-1}{x^2-1} \div \dfrac{3x-2}{x^2-1}\\[5pt] & = \dfrac{2x^2-1}{x^2-1} \cdot \dfrac{x^2-1}{3x-2}\\[5pt] & = \dfrac{\left(2x^2-1\right)\left(x^2-1\right)}{\left(x^2-1\right)(3x-2)} \\[5pt] & = \dfrac{2x^2-1}{3x-2} & & \\ \end{align*}\nonumber\]
A few remarks about the previous example are in order. Note that the the functions \(f(x)\), \(g(x)\) and \(h(x)\) all simplify to the same thing. However, only two of these functions are actually equal. For two functions to be equal, they need, among other things, to have the same domain. Since \(f(x) = g(x)\) when simplified and \(f\) and \(g\) have the same domain, they are equal functions. Even though \(h(x)\) simplifies to be the same as \(f\) and \(g\), the domain of \(h\) is different than the domain of \(f\) and \(g\), and thus \(h\) is a different function.
Vertical Asymptotes
We now turn our attention to the graphs of rational functions. Let's first focus on how these functions behave near values that are not in the domain. Consider the function \(f(x) = \dfrac{2x-1}{x+1}\) from the previous example. Using a graphing calculator, we obtain the following graph:
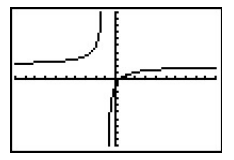
(note that older graphing calculator technologies will show a slightly different graph due to graphing limitations)
Note that the graph appears to 'break' at \(x=-1\). We know from our last example that \(x=-1\) is not in the domain of \(f\) which means \(f(-1)\) is undefined. When we make a table of values to study the behavior of \(f\) near \(x=-1\) we see that we can get 'near' \(x=-1\) from two directions. We can choose values a little less than \(-1\), for example \(x=-1.1\), \(x=-1.01\), \(x=-1.001\), and so on. These values are said to 'approach \(-1\) from the left.' Similarly, the values \(x=-0.9\), \(x=-0.99\), \(x=-0.999\), etc., are said to 'approach \(-1\) from the right.' If we make two tables, we find that the numerical results confirm what we see graphically.
|
|
As the \(x\) values approach \(-1\) from the left, the function values become larger and larger. We express this symbolically as \(x \rightarrow -1^{-}\), \(f(x) \rightarrow \infty\). Similarly, we conclude from the table that as \(x \rightarrow -1^{+}\), \(f(x) \rightarrow -\infty\). For this type of unbounded behavior, we say the graph of \(y=f(x)\) has a vertical asymptote of \(x = -1\). Roughly speaking, this means that near \(x=-1\), the graph looks very much like the vertical line \(x=-1\).
The line \(x=c\), where \(c\) is a real number, is called a vertical asymptote of the graph of a function \(y=f(x)\) if as \(x \rightarrow c^{-}\) or as \(x \rightarrow c^{+}\), either \(f(x) \rightarrow \infty\) or \(f(x) \rightarrow -\infty\).
Let's revisit \(h(x) = \dfrac{2x^2-1}{x^2-1} - \dfrac{3x-2}{x^2-1}\). We discussed that although \(h(x)\) simplified to \(\dfrac{2x-1}{x+1}\), the functions \(f\) and \(h\) are different since \(x=1\) is in the domain of \(f\) but \(x=1\) is not in the domain of \(h\). If we graph \(h(x)\) using a graphing calculator, we will get a graph that looks identical to \(y=f(x)\). There is a vertical asymptote at \(x=-1\), but near \(x=1\), everything seem fine. Tables of values provide numerical evidence which supports the graphical observation.
|
|
We see that as \(x \rightarrow 1^{-}\), \(h(x) \rightarrow 0.5^{-}\) and as \(x \rightarrow 1^{+}\), \(h(x) \rightarrow 0.5^{+}\). In other words, the points on the graph of \(y=h(x)\) are approaching \((1,0.5)\), which we can summarize as \(x \rightarrow 1\), \(h(x) \rightarrow 0.5\). Since \(x=1\) is not in the domain of \(h\), we put an open circle, also called a hole or removable discontinuity, at \((1,0.5)\). Below is a graph of \(h(x)\) with the hole drawn in. Note that most graphing technologies do not sketch holes.
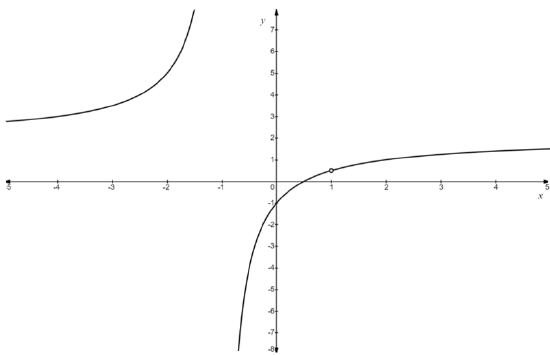
We have seen that values excluded from the domain will yield a vertical asymptote or a hole for the graph. How do we know which graphical behavior will occur at a value not in the domain? Notice that when we simplified \(h\), we had \(h(x) = \dfrac{(2x-1)(x-1)}{(x+1)(x-1)}\). The factor \((x-1)\) cancels whereas \((x+1)\) does not. Loosely speaking, the trouble caused by \((x-1)\) in the denominator is canceled away while the factor \((x+1)\) remains to cause mischief. This is why the graph of \(y=h(x)\) has a vertical asymptote at \(x=-1\) but only a hole at \(x=1\). These observations are generalized and summarized in the theorem below, whose proof is found in Calculus.
Suppose \(r\) is a rational function which can be written as \(r(x) = \dfrac{p(x)}{q(x)}\) where \(p\) and \(q\) have no common zeros {in other words, \(r(x)\) is in lowest terms.}. Let \(c\) be a real number which is not in the domain of \(r\).
- If \(q(c) \neq 0\), then the graph of \(y=r(x)\) has a hole at \(\left(c, \dfrac{p(c)}{q(c)}\right)\).
- If \(q(c) = 0\), then the line \(x=c\) is a vertical asymptote of the graph of \(y=r(x)\).
This theorem says that if \(x=c\) is not in the domain of \(r\) but, when we simplify \(r(x)\), it no longer makes the denominator \(0\), then we have a hole at \(x=c\). Otherwise, the line \(x=c\) is a vertical asymptote of the graph of \(y=r(x)\).
Find the vertical asymptotes and/or holes in the graphs of the following rational functions. Describe the behavior of the graph near them using proper notation.
- \(f(x) = \dfrac{2x}{x^2-3}\)
- \(g(x) = \dfrac{x^2-x-6}{x^2-9}\)
- \(h(x) = \dfrac{x^2-x-6}{x^2+9}\)
- \(r(x) = \dfrac{x^2-x-6}{x^2+4x+4}\)
Solution
- To find the domain, we solve \(x^2 - 3 = 0\) and get \(x = \pm \sqrt{3}\). Since the expression \(f(x)\) is in lowest terms, there is no cancellation possible, and we conclude that the lines \(x = -\sqrt{3}\) and \(x=\sqrt{3}\) are vertical asymptotes to the graph of \(y=f(x)\). As \(x \rightarrow -\sqrt{3}^{\, -}\), \(f(x) \rightarrow -\infty\), as \(x\rightarrow -\sqrt{3}^{\, +}\), \(f(x) \rightarrow \infty\), as \(x \rightarrow \sqrt{3}^{\, -}\), \(f(x) \rightarrow -\infty\), and finally as \(x\rightarrow \sqrt{3}^{\, +}\), \(f(x) \rightarrow \infty\).
- Solving \(x^2 - 9 = 0\) gives \(x = \pm 3\). In lowest terms \(g(x) = \dfrac{x^2-x-6}{x^2-9} = \dfrac{(x-3)(x+2)}{(x-3)(x+3)} = \dfrac{x+2}{x+3}\). Since \(x+3\) continues to make trouble in the denominator, the line \(x=-3\) is a vertical asymptote of the graph of \(y=g(x)\). Since \(x-3\) cancelled out, we have a hole at \(x=3\). To find the \(y\)-coordinate of the hole, we substitute \(x=3\) into the simplified expression, \(\dfrac{x+2}{x+3}\), and find the hole is at \(\left(3, \dfrac{5}{6}\right)\). As \(x \rightarrow -3^{-}\), \(g(x) \rightarrow \infty\), as \(x \rightarrow -3^{+}\), \(g(x) \rightarrow -\infty\), as \(x \rightarrow 3^{-}\), \(g(x) \rightarrow \dfrac{5}{6}^{-}\), and as \(x \rightarrow 3^{+}\), \(g(x) \rightarrow \dfrac{5}{6}^{+}\).
3. The domain of \(h\) is all real numbers, since \(x^2+9 = 0\) has no real solutions. Hence, the graph of \(y=h(x)\) has no vertical asymptotes or holes.
4. Setting \(x^2+4x+4 = 0\) gives us \(x=-2\). Simplifying, we see \[r(x) = \dfrac{x^2-x-6}{x^2+4x+4} = \dfrac{(x-3)(x+2)}{(x+2)^2} = \dfrac{x-3}{x+2}\nonumber\] Since \(x=-2\) continues to produce a \(0\) in the denominator of the reduced function, we know \(x=-2\) is a vertical asymptote to the graph. As \(x\rightarrow -2^{-}\), \(r(x) \rightarrow \infty\) and as \(x \rightarrow -2^{+}\), \(r(x) \rightarrow -\infty\).
Our next example gives us a physical interpretation of a vertical asymptote. This type of model arises from a family of equations cheerily named 'doomsday' equations. These functions arise in Differential Equations. The unfortunate name will make sense shortly.
A mathematical model for the population \(P\), in thousands, of a certain species of bacteria, \(t\) days after it is introduced to an environment is given by \(P(t) = \dfrac{100}{(5-t)^{2}}\), \(0 \leq t < 5\).
- Find and interpret \(P(0)\).
- When will the population reach \(100,\!000\)?
- Determine the behavior of \(P\) as \(t \rightarrow 5^{-}\). Interpret this result graphically and within the context of the problem.
Solution
- Substituting \(t=0\) gives \(P(0) = \dfrac{100}{(5-0)^2} = 4\), which means \(4000\) bacteria are initially introduced into the environment.
- To find when the population reaches \(100,\! 000\), we first need to remember that \(P(t)\) is measured in thousands. In other words, \(100,\! 000\) bacteria corresponds to \(P(t) = 100\). Substituting for \(P(t)\) gives the equation \(\dfrac{100}{(5-t)^2} = 100\). Clearing denominators and dividing by \(100\) gives \((5-t)^2=1\), which, after extracting square roots, produces \(t = 4\) or \(t=6\). Of these two solutions, only \(t=4\) in in our domain, so this is the solution we keep. Hence, it takes \(4\) days for the population of bacteria to reach \(100,\! 000\).
- To determine the behavior of \(P\) as \(t \rightarrow 5^{-}\), we can make a table
| t | P(t) |
|---|---|
| 4.9 | 10000 |
| 4.99 | 1000000 |
| 4.999 | 100000000 |
| 4.9999 | 10000000000 |
In other words, as \(t \rightarrow 5^{-}\), \(P(t) \rightarrow \infty\). Graphically, the line \(t=5\) is a vertical asymptote of the graph of \(y=P(t)\). Physically, this means that the population of bacteria is increasing without bound as we near 5 days, which cannot actually happen. For this reason, \(t=5\) is called the 'doomsday' for this population. There is no way any environment can support infinitely many bacteria, so shortly before \(t = 5\) the environment would collapse.
Horizontal Asymptotes
Now that we have thoroughly investigated behavior or rational functions around values not in the domain, let's turn our attention to end behavior of these functions. Recall the graph of the function \(y=f(x)=\dfrac{2x-1}{x+1}\) that we were discussing earlier. Notice that the graph of \(f\) seems to 'level off' on the left and right hand sides of the screen. This is a statement about the end behavior of the function. Looking at a tables of values to investigate what happens as \(x\) gets larger and larger and also more and more negative without bound, we find
|
|
|
From the tables, we see that as \(x \rightarrow -\infty\), \(f(x) \rightarrow 2\) and as \(x \rightarrow \infty\), \(f(x) \rightarrow 2\). In this case, we say the graph of \(y=f(x)\) has a horizontal asymptote of \(y=2\). This means that the end behavior of \(f\) resembles the horizontal line \(y=2\), which explains the 'leveling off' behavior we see in the calculator's graph.
The line \(y=c\), where \(c\) is a real number, is called a horizontal asymptote of the graph of a function \(y=f(x)\) if as \(x \rightarrow -\infty\) or as \(x \rightarrow \infty\), \(f(x) \rightarrow c\).
Note that in in this definition, we write \(f(x) \rightarrow c\) (not \(f(x) \rightarrow c^{+}\) or \(f(x) \rightarrow c^{-}\)) because we are unconcerned from which direction the values \(f(x)\) approach the value \(c\), just as long as they do so.
Suppose \(r\) is a rational function and \(r(x) = \dfrac{p(x)}{q(x)}\), where \(p\) and \(q\) are polynomial functions with leading coefficients \(a\) and \(b\), respectively.
- If the degree of \(p(x)\) is the same as the degree of \(q(x)\), then \(y=\dfrac{a}{b}\) is the horizontal asymptote of the graph of \(r(x)\).
- If the degree of \(p(x)\) is less than the degree of \(q(x)\), then \(y=0\) is the horizontal asymptote of the graph of \(r(x)\).
- If the degree of \(p(x)\) is greater than the degree of \(q(x)\), then the graph of \(r(x)\) has no horizontal asymptotes.
You may be wondering why the existence of horizontal asymptotes for rational functions is dependent upon the degree of the numerator and denominator. Remember that rational functions are division of polynomials. Let's revisit division for a moment to discover why. Using our example \(f(x) = \dfrac{2x-1}{x+1}\) and division, we can write \(f\) as \(\dfrac{2x-1}{x+1} = 2 - \dfrac{3}{x+1}\). As \(x\) becomes unbounded in either direction, the quantity \(\dfrac{3}{x+1}\) gets closer and closer to \(0\) so that the values of \(f(x)\) become closer and closer to \(2\) (you can verify this using tables). In symbols, as \(x \rightarrow \pm \infty\), \(f(x) \rightarrow 2\). By definition, this indicates \(f\) has a horizontal asymptote at \(y=2\).
Alternatively, we can use what we know about end behavior of polynomials to help us understand this theorem. We know the end behavior of a polynomial is determined by its leading term. Applying this to the numerator and denominator of \(f(x)\), we get that as \(x \rightarrow \pm \infty\), \(f(x) = \dfrac{2x-1}{x+1} \approx \dfrac{2x}{x} = 2\).
Applying this reasoning to the general case, suppose \(r(x) = \dfrac{p(x)}{q(x)}\) where \(a\) is the leading coefficient of \(p(x)\) and \(b\) is the leading coefficient of \(q(x)\). As \(x \rightarrow \pm \infty\), \(r(x) \approx \dfrac{ax^n}{bx^m}\), where \(n\) and \(m\) are the degrees of \(p(x)\) and \(q(x)\), respectively. If the degree of \(p(x)\) and the degree of \(q(x)\) are the same, then \(n=m\) so that \(r(x) \approx \dfrac{a}{b}\), which means \(y=\dfrac{a}{b}\) is the horizontal asymptote in this case. If the degree of \(p(x)\) is less than the degree of \(q(x)\), then \(n < m\), so \(m-n\) is a positive number, and hence, \(r(x) \approx \dfrac{a}{bx^{m-n}} \rightarrow 0\) as \(x \rightarrow \pm \infty\). If the degree of \(p(x)\) is greater than the degree of \(q(x)\), then \(n > m\), and hence \(n-m\) is a positive number and \(r(x) \approx \dfrac{ax^{n-m}}{ b}\), which becomes unbounded as \(x \rightarrow \pm \infty\).
List the horizontal asymptotes, if any, of the graphs of the following functions. Describe the behavior of the graph near them using proper notation.
- \(f(x) = \dfrac{5x}{x^2+1}\)
- \(g(x) = \dfrac{x^2-4}{x+1}\)
- \(h(x) = \dfrac{6x^3-3x+1}{5-2x^3}\)
Solution
- The numerator of \(f(x)\) is \(5x\), which has degree \(1\). The denominator of \(f(x)\) is \(x^2+1\), which has degree \(2\). Since the degree of the numerator is less than the denominator, \(y=0\) is the horizontal asymptote. As \(x \rightarrow - \infty\), \(f(x) \rightarrow 0^{-}\) and as \(x \rightarrow \infty\), \(f(x) \rightarrow 0^{+}\).
- The numerator of \(g(x)\), \(x^2-4\), has degree \(2\), but the degree of the denominator, \(x+1\), has degree \(1\). Since the degree of the numerator is larger thant he denominator, here is no horizontal asymptote. {Sit tight! We'll revisit this function and its end behavior shortly.}
- The degrees of the numerator and denominator of \(h(x)\) are both three, so \(y = \dfrac{6}{-2} = -3\) is the horizontal asymptote. As \(x \rightarrow -\infty\), \(h(x) \rightarrow -3^{+}\), and as \(x \rightarrow \infty\), \(h(x) \rightarrow -3^{-}\).
Slant Asymptotes
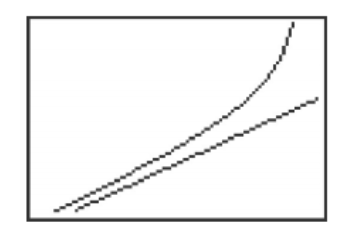
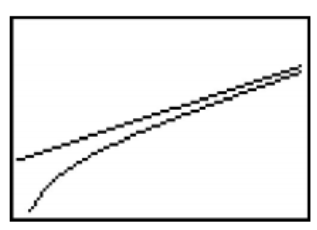
In the previous example, \(g(x) = \dfrac{x^2-4}{x+1}\), did not have a horizontal asymptote. What is the end behavior of this function then? Performing long division, we get \(g(x) = \dfrac{x^2-4}{x+1} = x-1 - \dfrac{3}{x+1}\). Since the term \(\dfrac{3}{x+1} \rightarrow 0\) as \(x \rightarrow \pm \infty\), it stands to reason that as \(x\) becomes unbounded, the function values \(g(x) = x-1 - \dfrac{3}{x+1} \approx x-1\). Geometrically, this means that the graph of \(y=g(x)\) should resemble the line \(y = x-1\) as \(x \rightarrow \pm \infty\). We see this play out both numerically and graphically below.
|
|
||||||||||||||||||||||||||||||
|
\(y=g(x)\) and \(y=x-1\) |
\(y=g(x)\) and \(y=x-1\) as \(x \rightarrow \infty\) |
The way we symbolize the relationship between the end behavior of \(y=g(x)\) with that of the line \(y=x-1\) is to write 'as \(x \rightarrow \pm \infty\), \(g(x) \rightarrow x-1\).' In this case, we say the line \(y=x-1\) is a slant asymptote of \(y=g(x)\). Informally, the graph of a rational function has a slant asymptote if, as \(x \rightarrow \infty\) or as \(x \rightarrow -\infty\), the graph resembles a non-horizontal, or 'slanted' line. Formally, we define a slant asymptote as follows.
The line \(y = mx+b\) where \(m \neq 0\) is called a slant asymptote of the graph of a function \(y=f(x)\) if as \(x \rightarrow -\infty\) or as \(x \rightarrow \infty\), \(f(x) \rightarrow mx+b\).
Note that the stipulation \(m \neq 0\) in this definition is what makes the 'slant' asymptote 'slanted' as opposed to the case when \(m=0\) in which case we'd have a horizontal asymptote.
Also, since \(y=x-1\) has the end behavior that \(y \rightarrow -\infty\) as \(x \rightarrow -\infty\) and \(y \rightarrow \infty\) as \(x \rightarrow \infty\) we can describe the end of behavior of g(x) as follows:
\(g(x) \rightarrow -\infty\) as \(x \rightarrow -\infty\) and \(g(x) \rightarrow \infty\) as \(x \rightarrow \infty\)
Some mathematicians prefer to describe the end behavior with the actual asymptote and some prefer to describe the end behavior directly like was just done above.
Our next task is to determine the conditions under which the graph of a rational function has a slant asymptote, and if it does, how to find it. In the case of \(g(x) = \dfrac{x^2-4}{x+1}\), the degree of the numerator \(x^2-4\) is \(2\), which is exactly one more than the degree if its denominator \(x+1\) which is \(1\). This results in a linear quotient polynomial, and it is this quotient polynomial which is the slant asymptote.
Suppose \(r\) is a rational function and \(r(x) = \dfrac{p(x)}{q(x)}\), where the degree of \(p\) is exactly one more than the degree of \(q\). Then the graph of \(y=r(x)\) has the slant asymptote \(y=L(x)\) where \(L(x)\) is the quotient obtained by dividing \(p(x)\) by \(q(x)\).
Find the slant asymptotes of the graphs of the following functions if they exist. Describe the end behavior of the graph near them using proper notation.
- \(f(x) = \dfrac{x^2-4x+2}{1-x}\)
- \(g(x) = \dfrac{x^2-4}{x-2}\)
- \(h(x) = \dfrac{x^3+1}{x^2-4}\)
Solution
- The degree of the numerator is \(2\) and the degree of the denominator is \(1\), so \(f\) has a slant asymptote. To find it, we divide \(1-x = -x+1\) into \(x^2-4x+2\) and get a quotient of \(-x+3\), so our slant asymptote is \(y=-x+3\). As \(x\rightarrow -\infty\) or as as \(x\rightarrow \infty\), \(f(x) \rightarrow (-x+3)\).
- The degree of the numerator \(g(x) = \dfrac{x^2-4}{x-2}\) is \(2\) and the degree of the denominator is \(1\). However, \[ g(x) = \dfrac{x^2-4}{x-2} = \dfrac{(x+2)(x-2)}{(x-2)} = x+2, x \neq 2\nonumber \] so we have that the slant asymptote \(y=x+2\) is identical to the graph of \(y=g(x)\) except at \(x=2\) (where the latter has a 'hole' at \((2,4)\).) As \(x\rightarrow -\infty\) and as \(x\rightarrow \infty\), \(g(x) \rightarrow (x+2)\).
- For \(h(x) = \dfrac{x^3+1}{x^2-4}\), the degree of the numerator is \(3\) and the degree of the denominator is \(2\) so again, we are guaranteed the existence of a slant asymptote. The long division \(\left(x^3+1 \right) \div \left(x^2-4\right)\) gives a quotient of just \(x\), so our slant asymptote is the line \(y=x\). As \(x \rightarrow -\infty\) and as \(x \rightarrow \infty\), \(g(x) \rightarrow x\)
Oblique Asymptotes
We have discussed the end behavior and asymptotes of rational functions where the degree of the numerator is less than, equal, or one degree higher than the degree of the denominator. You may be wondering about the end behavior of rational functions where the degree of the numerator is a degree of at least two or larger than the degree of the denominator. We know from polynomial division that the quotient will be a polynomial. Since rational functions are division of polynomials that means that the quotient will describe the end behavior of the rational function in a similar way as slant asymptotes do.
The function \(f(x)=\dfrac{x^4+x^3-2x^2+3}{x^2+x-2}\) can be rewritten as \(f(x)=x^2+\dfrac{3}{x^2+x-2}\). As \(x \rightarrow \pm \infty\), \(f(x)\rightarrow x^2\). So, the end behavior for \(f\) is as \(x \rightarrow \pm \infty\), \(f(x) \rightarrow \infty\). We call \(y=x^2\) an oblique asymptote. When graphing \(f\) and the oblique asymptote together, visually can see that, in fact, \(f(x)\rightarrow x^2\) as \(x \rightarrow \pm \infty\).
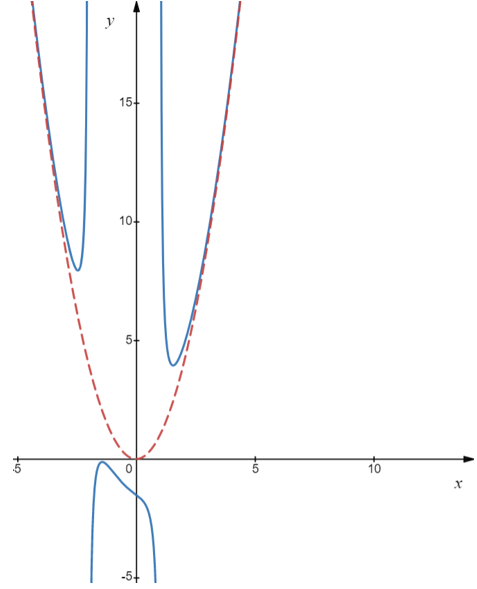
Some mathematicians will say that horizontal and/or slant asymptotes are types of oblique asymptotes. Others will argue that oblique asymptotes are strictly polynomials of degree two or higher. We are not in a position to argue that one description is better than another. This main thing is to be aware that the end behavior of rational functions is polynomial in nature. For this text, we will summarize the end behavior into three categories of asymptotes as follows:
For a rational function, \(r(x)\), as \(x \rightarrow \pm \infty\)
- If \(r(x)\rightarrow c\) where \(c\) is a real number, then \(y=c\) is a horizontal asymptote for \(r(x)\).
- If \(r(x)\rightarrow mx+b\) where \(m\) and \(b\) are real numbers and \(m \neq0\), then \(y=mx+b\) is a slant asymptote for \(r(x)\).
- If \(r(x)\rightarrow P(x)\) where \(P(x)\) is a polynomial of degree 2 or higher, then \(y=P(x)\) is a slant asymptote for \(r(x)\).