Prime Numbers

Last updated
Save as PDF

Page ID: 30970

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Prime Numbers

We begin with the definition of a prime number.

Prime Number

A whole number (other than 1) is a prime number if its only factors (divisors) are 1 and itself. Equivalently, a number is prime if and only if it has exactly two factors (divisors).

Example 3

Which of the whole numbers 12, 13, 21, and 37 are prime numbers?

Solution

The factors (divisors) of 12 are 1, 2, 3, 4, 6, and 12. Hence, 12 is not a prime number.
The factors (divisors) of 13 are 1 and 13. Because its only divisors are 1 and itself, 13 is a prime number.
The factors (divisors) of 21 are 1, 3, 7, and 21. Hence, 21 is not a prime number.
The factors (divisors) of 37 are 1 and 37. Because its only divisors are 1 and itself, 37 is a prime number.

Exercise

Which of the whole numbers 15, 23, 51, and 59 are prime numbers?

Answer: 23 and 59

Example 4

List all the prime numbers less than 20.

Solution

The prime numbers less than 20 are 2, 3, 5, 7, 11, 13, 17, and 19.

You try it!

List all the prime numbers less than 100.

Composite Numbers

If a whole number is not a prime number, then it is called a composite number.

Example 5

Is the whole number 1,179 prime or composite?

Solution

Note that 1 + 1 + 7 + 9 = 18, which is divisible by both 3 and 9. Hence, 3 and 9 are both divisors of 1,179. Therefore, 1,179 is a composite number.

Exercise

Is the whole number 2,571 prime or composite?

Answer: Composite

Factor Trees

We will now learn how to express a composite number as a unique product of prime numbers. The most popular device for accomplishing this goal is the factor tree.

Example 6

Express 24 as a product of prime factors.

Solution

We use a factor tree to break 24 down into a product of primes.

$Screen Shot 2019-08-07 at 8.00.41 PM.png$

At each level of the tree, break the current number into a product of two factors. The process is complete when all of the “circled leaves” at the bottom of the tree are prime numbers. Arranging the factors in the “circled leaves” in order,

24 = 2 · 2 · 2 · 3.

The final answer does not depend on product choices made at each level of the tree. Here is another approach.

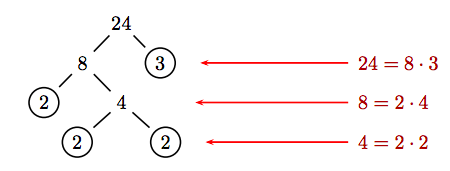
$Screen Shot 2019-08-07 at 8.00.48 PM.png$

The final answer is found by including all of the factors from the “circled leaves” at the end of each branch of the tree, which yields the same result, namely 24 = 2 · 2 · 2 · 3.

Alternate Approach

Some favor repeatedly dividing by 2 until the result is no longer divisible by 2. Then try repeatedly dividing by the next prime until the result is no longer divisible by that prime. The process terminates when the last resulting quotient is equal to the number 1.

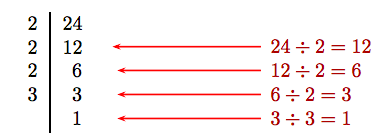
$Screen Shot 2019-08-07 at 8.00.56 PM.png$

The first column reveals the prime factorization; i.e., 24 = 2 · 2 · 2 · 3.

Exercise

Express 36 as a product of prime factors.

Answer: 2 · 2 · 3 · 3.

The fact that the alternate approach in Example 6 yielded the same result is significant.

Unique Factorization Theorem

Every whole number can be uniquely factored as a product of primes.

This result guarantees that if the prime factors are ordered from smallest to largest, everyone will get the same result when breaking a number into a product of prime factors.