6.2: Inequalities
- Last updated
- Save as PDF
- Page ID
- 31024
In Chapter 1, we introduced the natural numbers \(\mathbb{N}=\{1,2,3, \ldots\}\), the whole numbers \(\mathbb{W}=\{0,1,2,3, \ldots\}\), and the integers \(\mathbb{Z}=\{\ldots,-3,-2,-1,0,1,2,3, \ldots\}\). Later in the chapter, we introduced the rational numbers, numbers of the form \(p/q\), where \(p\) and \(q\) are integers. We noted that both terminating and repeating decimals are rational numbers. Each of these numbers has a unique position on the number line (see Figure \(\PageIndex{1}\) ).

The natural numbers, whole numbers, and integers are also rational numbers, because each can be expressed in the form \(\frac{p}{q}\), where \(p\) and \(q\) are integers. For example, \(0=\frac{0}{12}\), \(4 = \frac{4}{1}\), and \(-3=\frac{-12}{4}\). Indeed, the rational numbers contain all of the numbers we’ve studied up to this point in the course. However, not all numbers are rational numbers. For example, consider the decimal number \(-3.10110111011110 \ldots\), which neither terminates nor repeats. The number \(\sqrt{2}=1.414213562373095 \ldots\) also equals a decimal number that never terminates and never repeats. A similar statement can be made about the number \(\pi=3.141592653589793 \dots\) Each of these irrational (not rational) numbers also has a unique position on the number line (see Figure \(\PageIndex{2}\)).

Two other irrational numbers you may encounter in your mathematical studies are \(e\) (Euler’s constant), which is approximately equal to \(e \approx 2.71828182845904 \ldots\), and \(\phi\) (pronounced “phi”), called the golden ratio, which equals \(\phi= \frac{1+\sqrt{5}}{2}\). The number \(e\) arises in applications involving compound interest, probability, and other areas of mathematics. The number \(\phi\) is used in financial markets and is also arguably the ratio of beauty in art and architecture.
The Real Numbers
If we combine all of the rational and irrational numbers into one collection, then we have a set of numbers that is called the set of real numbers. The set of real numbers is denoted by the symbol \(\mathbb{R}\).
Every point on the number line is associated with a unique real number. Conversely, every real number is associated with a unique position on the number line. In lieu of this correspondence, the number line is usually called the real line.
Ordering the Real Numbers
The real numbers are ordered on the real line in a manner identical to how we ordered the integers on the number line in Section 1 of Chapter 1.
Order on the Real Line
Suppose that \(a\) and \(b\) are real numbers positioned on the real line as shown below.

- Because \(a\) lies to the “left of” \(b\), we say that \(a\) is “less than” \(b\), or in mathematical symbols, \(a<b\). The inequality symbol \(<\) is read “less than.”
- Alternately, \(b\) lies to the “right of” \(a\), so we can also say that \(b\) is “greater than” \(a\), or in mathematical symbols, \(b>a\). The inequality symbol \(>\) is read “greater than.”
Here are two more inequality symbols that we will use in this section.
Less than or equal to
If we want to say that \(a\) lies to the “left of” \(b\), or shares the same position as \(b\), then we say that \(a\) is “less than or equal to” \(b\) and write \(a ≤ b\). The inequality symbol \(≤\) is pronounced “less than or equal to.”
Greater than or equal to
If we want to say that \(b\) lies to the “right of” \(a\), or shares the same position as \(a\), then we say that \(b\) is “greater than or equal to" \(a\) and write \(b≥ a\). The inequality symbol \(≥\) is pronounced “greater than or equal to.”
Set-Builder Notation
Mathematicians use a construct called set-builder notation to describe sets or collections of numbers. The general form of set-builder notation looks as follows: \[\{x : \text { some statement about } x\} \nonumber \]For example, suppose that we want to describe the set of “all real numbers that are less than \(2\).” We could use the following notation: \[A=\{x : x<2\} \nonumber \]
This is read aloud as follows: “\(A\) equals the set of all \(x\) such that \(x\) is less than \(2\).” Some prefer to use a vertical bar instead of a colon. \[A=\{x \, | \, x<2\} \nonumber \] In this text we use the colon in set-builder notation, but feel free to use the vertical bar instead. They mean the same thing. One might still object that the notation \[\{x : x<2\} \nonumber \] is a bit vague. One objection could be “What type of numbers \(x\) are you referring to? Do you want the integers that are less than two or do you want the real numbers that are less than two?” As you can see, this is a valid objection. One way of addressing this objection is to write: \[A=\{x \in \mathbb{R} : x<2\} \quad \text { or } \quad A=\{x \in \mathbb{N} : x<2\} \nonumber \] The first is read “\(A\) is the set of all \(x\) in \(R\) that are less than two,” while the second is read “\(A\) is the set of all \(x\) in \(N\) that are less than two.”
Set-builder Assumption
In this text, unless there is a specific reference to the set of numbers desired, we will assume that the notation \(\{x : x<2\}\) is asking for the set of all real numbers less than \(2\).
In Figure \(\PageIndex {3}\), we’ve shaded the set of real numbers \(\{x : x<2\}\). Because

“less than” is the same as saying “left of,” we’ve shaded (in red) all points on the real line that lie to the left of the number two. Note that there is an “empty circle” at the number two. The point representing the number two is not shaded because we were only asked to shade the numbers that are strictly less than two.
While the shading in Figure \(\PageIndex{3}\) is perfectly valid, much of the information provided in Figure \(\PageIndex{3}\) is unnecessary (and perhaps distracting). We only need to label the endpoint and shade the real numbers to the left of two, as we’ve done in constructing Figure \(\PageIndex{4}\).

For contrast, suppose instead that we’re asked to shade the set of real numbers \(\{x : x\leq2\}\). This means that we must shade all the real numbers

that are “less than or equal to \(2\)” or “left of and including \(2\).” The resulting set is shaded in Figure \(\PageIndex{5}\).
Note the difference between Figures \(\PageIndex{4}\) and \(\PageIndex{45}\). In Figures \(\PageIndex{4}\) we’re shading the set \(\{x : x<2\}\), so the number \(2\) is left unshaded (an empty dot). In Figures \(\PageIndex{5}\), we’re shading the set \(\{x : x\leq2\}\), so the number \(2\) is shaded (a filled-in dot).
Example \(\PageIndex{1}\)
Shade the set \(\{x : x \geq-3\}\) on the real line.
Solution
The notation \(\{x : x \geq-3\}\) is pronounced “the set of all real numbers \(x\) such that \(x\) is greater than or equal to \(-3\).” Thus, we need to shade the number \(-3\) and all real numbers to the right of \(-3\).

Exercise \(\PageIndex{1}\)
Shade \(\{x : x \leq 4\}\) on the real line.
- Answer
-

Example \(\PageIndex{2}\)
Use set-builder notation to describe the set of real numbers that are shaded on the number line below.

Solution
The number \(-1\) is not shaded. Only the numbers to the left of \(-1\) are shaded. This is the set of all real numbers \(x\) such that \(x\) is “less than” \(-1\). Thus, we describe this set with the following set-builder notation: \[\{x : x<-1\} \nonumber \]
Exercise \(\PageIndex{2}\)
Use set-builder notation to describe the following set of real numbers:
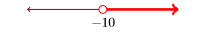
- Answer
-
\(\{x : x>-10\}\)
Interval Notation
In Examples \(\PageIndex{1}\) and \(\PageIndex{2}\), we used set-builder notation to describe the set of real numbers greater than or equal to \(-3\) and a second set of real numbers less than \(-1\). There is another mathematical symbolism, called interval notation, that can be used to describe these sets of real numbers. Consider the first set of numbers from Example \(\PageIndex{1}\), \(\{x : x \geq-3\}\).

Sweeping our eyes “from left to right”, we use \([-3, \infty)\) to describe this set of real numbers. Some comments are in order:
- The bracket at the left end means that \(-3\) is included in the set.
- As you move toward the right end of the real line, the numbers grow without bound. Hence, the \(\infty\) symbol (positive infinity) is used to indicate that we are including all real numbers to the right of \(-3\). However, \(\infty\) is not really a number, so we use a parentheses to indicate we are “not including” this fictional point.
The set of numbers from Example \(\PageIndex {1}\) is \(\{x : x<-1\}\).

Sweeping our eyes “from left to right”, this set of real numbers is described with \((-\infty,-1)\). Again, comments are in order:
- The number \(-1\) is not included in this set. To indicate that it is not included, we use a parenthesis.
- As you move toward the left end of the real line, the numbers decrease without bound. Hence, the \(-\infty\) symbol (negative infinity) is used to indicate that we are including all real numbers to the left of \(-1\). Again, \(-\infty\) is not an actual number, so we use a parenthesis to indicate that we are not including this “fictional” point.
Sweep your eyes from “left to right”
If you would like to insure that you correctly use interval notation, place the numbers in your interval notation in the same order as they are encountered as you sweep your eyes from “left to right” on the real line.
A nice summary of set-builder and interval notation is presented in Table \(\PageIndex{1}\) at the end of the section.
Equivalent Inequalities
Like equations, two inequalities are equivalent if they have the same solution sets.
Adding or Subtracting the Same Quantity from Both Sides of an Inequality
Let \(a\) and \(b\) be real numbers with \[a < b \nonumber \]
If \(c\) is any real number, then \[a + c<b+ c \nonumber \]and\[a−c<b−c \nonumber \]That is, adding or subtracting the same amount from both sides of an inequality produces an equivalent inequality (does not change the solution).
Example \(\PageIndex{3}\)
Solve for \(x: \quad x-2 ≤ 7\). Sketch the solution on the real line, then use set-builder and interval notation to describe your solution.
Solution
To “undo” subtracting \(2\), we add \(2\) to both sides of the inequality.
\[\begin{aligned} x-2 &\leq 7 & & \color {Red} \text { Original inequality. } \\ x-2+2 &\leq 7+2 & & \color {Red} \text { Add } 2 \text { to both sides. } \\ x &\leq 9 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]
To shade the real numbers less than or equal to \(9\), we shade the number \(9\) and all real numbers to the left of \(9\).

Using set-builder notation, the solution is \(\{x : x \leq 9\}\). Using interval notation, the solution is \((-\infty, 9]\).
Exercise \(\PageIndex{3}\)
Use interval notation to describe the solution of: \(x−7 < −8\).
- Answer
-
\((-\infty,-1)\)
If we multiply or divide both sides of an inequality by a positive number, we have an equivalent inequality.
Multiplying or Dividing by a Positive Number
Let \(a\) and \(b\) be real numbers with \(a<b\). If \(c\) is a real positive number, then \[a c<b c \nonumber \]and\[\dfrac{a}{c}<\dfrac{b}{c} \nonumber \]
Example \(\PageIndex{4}\)
Solve for \(x : \quad 3 x \leq-9\) Sketch the solution on the real line, then use set-builder and interval notation to describe your solution.
Solution
To “undo” multiplying by \(3\), divide both sides of the inequality by \(3\). Because we are dividing both sides by a positive number, we do not reverse the inequality sign.
\[\begin{aligned} 3x & \leq -9 & & \color {Red} \text { Original inequality. } \\ \dfrac{3x}{3} & \leq \dfrac{-9}{3} & & \color {Red} \text { Divide both sides by } 3. \\ x & \leq -3 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]
Shade the real numbers less than or equal to \(-3\).

Using set-builder notation, the solution is \(\{x : x \leq-3\}\). Using interval notation, the solution is \((-\infty,-3]\).
Exercise \(\PageIndex{4}\)
Use interval notation to describe the solution of: \[2 x>-8 \nonumber \]
- Answer
-
\((-4, \infty)\)
Reversing the Inequality Sign
Up to this point, it seems that the technique for solving inequalities is pretty much identical to the technique used to solve equations. However, in this section we are going to encounter one exception.
Suppose we start with the valid inequality \(-2 < 5\), then we multiply both sides by \(2\), \(3\), and \(4\).
\[\begin{array}{rrrr}{-2<5} & {-2<5} & {-2<5} \\ {2(-2)<2(5)} & {3(-2)<3(5)} & {4(-2)<4(5)} \\ {-4<10} & {-6<15} & {-8<20}\end{array} \nonumber \]
Note that in each case, the resulting inequality is still valid.
\(\color{Red} \text {Caution! We’re about to make an error!} \)
Start again with \(−2 < 5\), but this time multiply both sides by \(−2\), \(−3\), and \(−4\).
\[\begin{array}{rrrr}{-2<5} & {-2<5} & {-2<5} \\ {-2(-2)<-2(5)} & {\;-3(-2)<-3(5)} & {\;-4(-2)<-4(5)} \\ {4<-10} & {6<-15} & {8<-20}\end{array} \nonumber \]
In each of the resulting inequalities, the inequality symbol is pointing the wrong way!
When you multiply both sides of an inequality by a negative number, you must reverse the inequality sign. Starting with \(−2 < 5\), multiply both sides by \(−2\), \(−3\), and \(−4\), but reverse the inequality symbol.
Some readers might prefer a more formal reason as to why we reverse the inequality when we multiply both sides by a negative number. Suppose that \(a<b\). Then, subtracting \(b\) from both sides gives the result \(a−b<0\). This means that \(a−b\) is a negative number. Now, if \(c\) is a negative number, then the product \((a−b)c\) is positive. Then:
\[\begin{aligned}(a-b) c &>0 \\ a c-b c &>0 \\ a c-b c+b c &>0+b c \\ a c &>b c \end{aligned} \nonumber \]
Thus, if you start with \(a<b\) and \(c<0\), then \(ac > bc\).
Multiplying or Dividing by a Negative Number
Let \(a\) and \(b\) be real numbers with \(a<b\). If \(c\) is a real negative number, then \[a c>b c \nonumber \] and \[\dfrac{a}{c}>\dfrac{b}{c} \nonumber \]That is, when multiplying or dividing both sides of an inequality by a negative number, you must reverse the inequality sign.
Example \(\PageIndex{5}\)
Solve for \(x: \quad −2x<4\). Sketch the solution on the real line, then use set-builder and interval notation to describe your solution.
Solution
To “undo” multiplying by \(−2\), divide both sides by \(−2\). Because we are dividing both sides by a negative number, we reverse the inequality sign.
\[\begin{aligned} -2 x&< 4 & & \color {Red} \text { Original inequality. } \\ \dfrac{-2x}{-2}&> \dfrac{4}{-2} & & \color {Red} \text { Divide both sides by }-2 \\ x&> -2 & & \color {Red} \text { Reverse the inequality sign. } \\ x&> -2 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]
Shade the real numbers greater than \(−2\).

Using set-builder notation, the solution is \(\{x : x>-2\}\). Using interval notation, the solution is \((-2, \infty)\).
Exercise \(\PageIndex{5}\)
Use interval notation to describe the solution of: \[−3x≥− 6 \nonumber \]
- Answer
-
\((-\infty, 2]\)
Multiple Steps
Sometimes you need to perform a sequence of steps to arrive at the solution.
Example \(\PageIndex{6}\)
Solve for \(x: \quad 2 x +5> −7\). Sketch the solution on the real line, then use set-builder and interval notation to describe your solution.
Solution
To “undo” adding \(5\), subtract \(5\) from both sides of the inequality.
\[\begin{aligned} 2x+5&> -7 & & \color {Red} \text { Original inequality. } \\ 2x+5-5&> -7-5 & & \color {Red} \text { Subtract } 5 \text { from both sides. } \\ 2x&> -12 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]
To “undo” multiplying by \(2\), divide both sides by \(2\). Because we are dividing both sides by a positive number, we do not reverse the inequality sign.
\[\begin{aligned} \dfrac{2x}{2}& >\dfrac{-12}{2} & & \color {Red} \text { Divide both sides by } 2 \\ x&> -6 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]
Shade the real numbers greater than \(−6\).

Using set-builder notation, the solution is \(\{x : x>-6\}\). Using interval notation, the solution is \((-6, \infty)\).
Exercise \(\PageIndex{6}\)
Use interval notation to describe the solution of: \[3x-2 ≤4 \nonumber \]
- Answer
-
\((-\infty, 2]\)
Example \(\PageIndex{7}\)
Solve for \(x: \quad 3 −5x ≤ 2x + 17\). Sketch the solution on the real line, then use set-builder and interval notation to describe your solution.
Solution
We need to isolate terms containing \(x\) on one side of the inequality. Start by subtracting \(2x\) from both sides of the inequality.
\[\begin{aligned} 3-5x &\leq 2x+17 & & \color {Red} \text { Original inequality. } \\ 3-5x-2x &\leq 2x+17-2x & & \color {Red} \text { Subtract } 2x \text { from both sides. } \\ 3-7x &\leq 17 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]
We continue to isolate terms containing \(x\) on one side of the inequality. Subtract \(3\) from both sides.
\[\begin{aligned} 3-7x-3 &\leq 17-3 & & \color {Red} \text { Subtract } 3 \text { from both sides. } \\ -7x &\leq 14 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]
To “undo” multiplying by \(−7\), divide both sides by \(−7\). Because we are dividing both sides by a negative number, we reverse the inequality sign.
\[\begin{aligned} \dfrac{-7x}{-7} &\geq \dfrac{14}{-7} & & \color {Red} \text { Divide both sides by }-7 \\ x &\geq-2 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Using set-builder notation, the solution is \(\{x : x \geq-2\}\). Using interval notation, the solution is \([-2, \infty)\).
Exercise \(\PageIndex{7}\)
Use interval notation to describe the solution of: \[4-x>2x +1 \nonumber \]
- Answer
-
\((-\infty, 1)\)
We clear fractions from an inequality in the usual manner, by multiplying both sides by the least common denominator.
Example \(\PageIndex{8}\)
Solve for \(x : \quad \quad \dfrac{3}{4}-\dfrac{x}{12}>\dfrac{1}{3}\).
Solution
First, clear the fractions from the inequality by multiplying both sides by the least common denominator, which in this case is \(12\).
\[\begin{aligned} \dfrac{3}{4}-\dfrac{x}{12} &>\dfrac{1}{3} & & \color {Red} \text { Original inequality. } \\ 12\left[\dfrac{3}{4}-\dfrac{x}{12}\right] &>\left[\dfrac{1}{3}\right] 12 & & \color {Red} \text { Multiply both sides by } 12.\\ 12\left[\dfrac{3}{4}\right]-12\left[\dfrac{x}{12}\right] &>\left[\dfrac{1}{3}\right] 12 & & \color {Red} \text { Distribute the } 12.\\ 9-x &>4 & & \color {Red} \text { Cancel and Multiply. } \end{aligned} \nonumber \]
To “undo” adding \(9\), subtract \(9\) from both sides.
\[\begin{aligned} 9-x-9 &> 4-9 & & \color {Red} \text { Subtract } 9 \text { from both sides. } \\ -x &> -5 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]
We could divide both sides by \(−1\), but multiplying both sides by \(−1\) will also do the job. Because we are multiplying both sides by a negative number, we reverse the inequality sign.
\[\begin{aligned} (-1)(-x) &< (-5)(-1) & & \color {Red} \text { Multiply both sides by }-1. \text { Reverse the inequality sign. } \\ x &< 5 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]
Shade the real numbers less than \(5\).

Using set-builder notation, the solution is \(\{x : x<5\}\). Using interval notation, the solution is \((-\infty, 5)\).
Exercise \(\PageIndex{8}\)
Use interval notation to describe the solution of: \[\dfrac{2 x}{3}-\dfrac{3}{4} \geq-\dfrac{3}{2} \nonumber \]
- Answer
-
\([-\frac{9}{8}, \infty)\)
We clear decimals from an inequality in the usual manner, by multiplying both sides by the appropriate power of ten.
Example \(\PageIndex{9}\)
Solve for \(x : \quad 3.25-1.2 x>4.6\).
Solution
First, clear the decimals from the inequality by multiplying both sides by \(100\), which moves each decimal point two places to the right.
\[\begin{aligned} 3.25-1.2 x &>4.6 & & \color {Red} \text { Original inequality. }\\ 325-120 x &>460 & & \color {Red} \text { Multiply both sides by } 100.\\ 325-120 x-325 &>460-325 & & \color {Red} \text { Subtract } 325 \text { from both sides. }\\ -120 x &>135 & & \color {Red} \text { Simplify both sides. } \\ \dfrac{-120 x}{-120} &<\dfrac{135}{-120} & & \color {Red} \text { Divide both sides by } -120. \text { Reverse the inequality sign.}\\ x &<-\dfrac{27}{24} & & \color {Red} \text {Reduce to lowest terms.} \end{aligned} \nonumber \]
Shade the real numbers less than \(−27/24\).

Using set-builder notation, the solution is \(\{x : x<-27 / 24\}\). Using interval notation, the solution is \((-\infty,-27 / 24)\).
Exercise \(\PageIndex{9}\)
Use interval notation to describe the solution of: \[2.3 x-5.62 \geq-1.4 \nonumber \]
- Answer
-
\(\big[\frac{211}{115}, \infty\big)\)
Summary Table of Set-Builder and Interval Notation
A summary table of the set-builder and interval notation is presented in Table \(\PageIndex{1}\).
| Shading on the real line | Set-builder | Interval |
|---|---|---|
 |
\(\{x : x>-5\}\) | \((-5, \infty)\) |
 |
\(\{x : x \geq-5\}\) | \([-5, \infty)\) |
 |
\(\{x : x<-5\}\) | \((-\infty,-5)\) |
 |
\(\{x : x \leq-5\}\) | \((-\infty,-5]\) |


