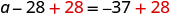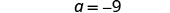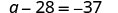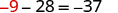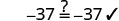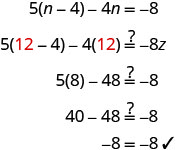2.1: Solve Equations Using the Subtraction and Addition Properties of Equality
- Last updated
- Save as PDF
- Page ID
- 18932
Learning Objectives
By the end of this section, you will be able to:
- Verify a solution of an equation
- Solve equations using the Subtraction and Addition Properties of Equality
- Solve equations that require simplification
- Translate to an equation and solve
- Translate and solve applications
Quiz
Before you get started, take this readiness quiz.
- Evaluate \(x+4\) when \(x=−3\).
If you missed this problem, review Exercise 1.5.25. - Evaluate \(15−y\) when \(y=−5\).
If you missed this problem, review Exercise 1.5.31. - Simplify \(4(4n+1)−15n\).
If you missed this problem, review Exercise 1.10.49. - Translate into algebra “5 is less than x.”
If you missed this problem, review Exercise 1.3.43.
Verify a Solution of an Equation
Solving an equation is like discovering the answer to a puzzle. The purpose in solving an equation is to find the value or values of the variable that make each side of the equation the same – so that we end up with a true statement. Any value of the variable that makes the equation true is called a solution to the equation. It is the answer to the puzzle!
Definition: Solution of an Equation
A solution of an equation is a value of a variable that makes a true statement when substituted into the equation.
TO DETERMINE WHETHER A NUMBER IS A Solution TO AN EQUATION
- Substitute the number in for the variable in the equation.
- Simplify the expressions on both sides of the equation.
- Determine whether the resulting equation is true (the left side is equal to the right side)
- If it is true, the number is a solution.
- If it is not true, the number is not a solution.
Example \(\PageIndex{1}\)
Determine whether \(x = \frac{3}{2}\) is a solution of \(4x−2=2x+1\).
Solution
Since a solution to an equation is a value of the variable that makes the equation true, begin by substituting the value of the solution for the variable.
| \(4 x-2=2 x+1\) | |
 |
\(4\left(\color{red}\frac{3}{2}\color{black}\right)-2 \stackrel{?}{=} 2\left(\color{red}\frac{3}{2}\color{black}\right)+1\) |
| Multiply. | \(6-2 \stackrel{?}{=} 3+1\) |
| Subtract. | \(4=4 \checkmark \) |
Since \(x = \frac{3}{2}\) results in a true equation (4 is in fact equal to 4), \(\frac{3}{2}\) is a solution to the equation \(4x−2=2x+1\).
Try It \(\PageIndex{2}\)
Is \(y = \frac{4}{3}\) a solution of \(9y+2=6y+3\)?
- Answer
-
no
Try It \(\PageIndex{3}\)
Is \(y = \frac{7}{5}\) a solution of \(5y+3=10y-4\)?
- Answer
-
yes
Solve Equations Using the Subtraction and Addition Properties of Equality
We are going to use a model to clarify the process of solving an equation. An envelope represents the variable – since its contents are unknown – and each counter represents one. We will set out one envelope and some counters on our workspace, as shown in Figure \(\PageIndex{1}\). Both sides of the workspace have the same number of counters, but some counters are “hidden” in the envelope. Can you tell how many counters are in the envelope?
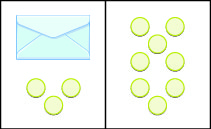
What are you thinking? What steps are you taking in your mind to figure out how many counters are in the envelope?
Perhaps you are thinking: “I need to remove the 3 counters at the bottom left to get the envelope by itself. The 3 counters on the left can be matched with 3 on the right and so I can take them away from both sides. That leaves five on the right—so there must be 5 counters in the envelope.” See Figure \(\PageIndex{2}\) for an illustration of this process.
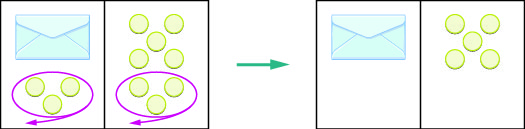
What algebraic equation would match this situation? In Figure \(\PageIndex{3}\) each side of the workspace represents an expression and the center line takes the place of the equal sign. We will call the contents of the envelope x.
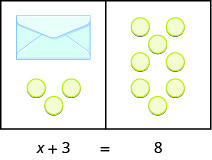
Let’s write algebraically the steps we took to discover how many counters were in the envelope:
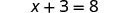 |
|
| First, we took away three from each side. |  |
| Then we were left with five. | 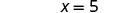 |
Check:
Five in the envelope plus three more does equal eight!
\[5+3=8\]
Our model has given us an idea of what we need to do to solve one kind of equation. The goal is to isolate the variable by itself on one side of the equation. To solve equations such as these mathematically, we use the Subtraction Property of Equality.
SUBTRACTION PROPERTY OF EQUALITY
For any numbers a, b, and c,
\[\begin{array} {ll} {\text{If}} &{a = b} \\ {\text{then}} &{a - c = b - c} \end{array}\]
When you subtract the same quantity from both sides of an equation, you still have equality.
Note
Doing the Manipulative Mathematics activity “Subtraction Property of Equality” will help you develop a better understanding of how to solve equations by using the Subtraction Property of Equality.
Let’s see how to use this property to solve an equation. Remember, the goal is to isolate the variable on one side of the equation. And we check our solutions by substituting the value into the equation to make sure we have a true statement.
Example \(\PageIndex{4}\)
Solve: \(y+37=−13\).
Solution
To get y by itself, we will undo the addition of 37 by using the Subtraction Property of Equality.
 |
||
| Subtract 37 from each side to ‘undo’ the addition. |  |
|
| Simplify. | 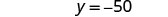 |
|
| Check: | 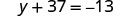 |
|
| Substitute \(y=−50\) | 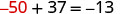 |
|
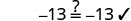 |
||
Since y=−50 makes y+37=−13 a true statement, we have the solution to this equation.
Try It \(\PageIndex{5}\)
Solve: \(x+19=−27\).
- Answer
-
\(x=−46\)
Try It \(\PageIndex{6}\)
Solve: \(x+16=−34\).
- Answer
-
\(x=−50\)
What happens when an equation has a number subtracted from the variable, as in the equation \(x−5=8\)? We use another property of equations to solve equations where a number is subtracted from the variable. We want to isolate the variable, so to ‘undo’ the subtraction we will add the number to both sides. We use the Addition Property of Equality.
ADDITION PROPERTY OF EQUALITY
For any numbers a, b, and c,
\[\begin{array} {ll} {\text{If}} &{a = b} \\ {\text{then}} &{a + c = b + c} \end{array}\]
When you add the same quantity from both sides of an equation, you still have equality.
In Exercise \(\PageIndex{4}\), 37 was added to the y and so we subtracted 37 to ‘undo’ the addition. In Exercise \(\PageIndex{7}\), we will need to ‘undo’ subtraction by using the Addition Property of Equality.
Try It \(\PageIndex{8}\)
Solve: \(n−61=−75\).
- Answer
-
\(n=−14\)
Try It \(\PageIndex{9}\)
Solve: \(p−41=−73\).
- Answer
-
\(p=−32\)
Example \(\PageIndex{10}\)
Solve: \(x - \frac{5}{8} = \frac{3}{4}\)
Solution
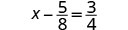 |
||
| Use the Addition Property of Equality. | 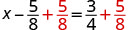 |
|
| Find the LCD to add the fractions on the right. | \(x-\frac{5}{8}+\frac{5}{8}=\frac{6}{8}+\frac{5}{8}\) | |
| Simplify. | \(x=\frac{11}{8}\) | |
| Check: | 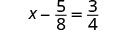 |
|
| Substitute \(x= \frac{11}{8}\) | 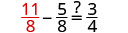 |
|
| Subtract. | 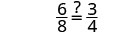 |
|
| Simplify. | 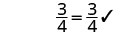 |
|
| The solution to \(x - \frac{5}{8} = \frac{3}{4}\) is \(x= \frac{11}{8}\). | ||
Try It \(\PageIndex{11}\)
Solve: \(p−\frac{2}{3}=\frac{5}{6}\).
- Answer
-
\(p = \frac{9}{6} p =\frac{3}{2}\)
Try It \(\PageIndex{12}\)
Solve: \(q−\frac{1}{2}=\frac{5}{6}\).
- Answer
-
\(q =\frac{4}{3}\)
The next example will be an equation with decimals.
Example \(\PageIndex{13}\)
Solve: \(n−0.63=−4.2\).
Solution
| \(n-0.63=-4.2\) | ||
| Use the Addition Property of Equality. |  |
|
| Add. | \(n=-3.57\) | |
| Check: | \(n=-3.57\) | |
| Let \(n=−3.57\). | 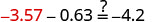 |
|
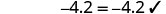 |
||
Try It \(\PageIndex{14}\)
Solve: \(b−0.47=−2.1\).
- Answer
-
\(b=−1.63\)
Try It \(\PageIndex{15}\)
Solve: \(c−0.93=−4.6\).
- Answer
-
\(c=−3.67\)
Solve Equations That Require Simplification
In the previous examples, we were able to isolate the variable with just one operation. Most of the equations we encounter in algebra will take more steps to solve. Usually, we will need to simplify one or both sides of an equation before using the Subtraction or Addition Properties of Equality.
You should always simplify as much as possible before you try to isolate the variable. Remember that to simplify an expression means to do all the operations in the expression. Simplify one side of the equation at a time. Note that simplification is different from the process used to solve an equation in which we apply an operation to both sides.
Example \(\PageIndex{16}\): How to Solve Equations That Require Simplification
Solve: \(9x−5−8x−6=7\).
Solution




Try It \(\PageIndex{17}\)
Solve: \(8y−4−7y−7=4\).
- Answer
-
\(y=15\)
Try It \(\PageIndex{18}\)
Solve: \(6z+5−5z−4=3\).
- Answer
-
\(z=2\)
Example \(\PageIndex{19}\)
Solve: 5(n−4)−4n=−8.
Solution
We simplify both sides of the equation as much as possible before we try to isolate the variable.
|
\(5(n-4)-4 n=-8\) |
|
| Distribute on the left. | \(5 n-20-4 n=-8\) |
| Use the Commutative Property to rearrange terms. | \(5 n-4 n-20=-8\) |
| Combine like terms. | \(n-20=-8\) |
| Each side is as simplified as possible. Next, isolate n. | |
| Undo subtraction by using the Addition Property of Equality. | \(n-20 \; \color{red}{+ 20} \;\color{black}{=-8}\; \color{red}{+20}\) |
| Add. | \(n=12\) |
|
Check. Substitute n=12.
|
|
| The solution to \(5(n−4)−4n=−8\) is \(n=12\). |
Try It \(\PageIndex{20}\)
Solve: \(5(p−3)−4p=−10\).
- Answer
-
\(p=5\)
Try It \(\PageIndex{21}\)
Solve: \(4(q+2)−3q=−8\).
- Answer
-
\(q=−16\)
Example \(\PageIndex{22}\)
Solve: \(3(2y−1)−5y=2(y+1)−2(y+3)\).
Solution
We simplify both sides of the equation before we isolate the variable.
| \(3(2 y-1)-5 y=2(y+1)-2(y+3)\) | |
| Distribute on both sides. | \(6 y-3-5 y=2 y+2-2 y-6\) |
| Use the Commutative Property of Addition. | \(6 y-5 y-3=2 y-2 y+2-6\) |
| Combine like terms. | \(y-3=-4\) |
| Each side is as simplified as possible. Next, isolate y. | |
| Undo subtraction by using the Addition Property of Equality. | \(y-3 \color{red} + 3 \color{black} = -4 \color{red} +3\) |
| Add. | \(y=-1\) |
Check. Let y=−1.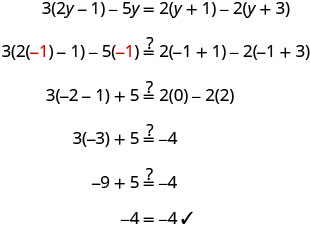 |
|
|
The solution to \(3(2y−1)−5y=2(y+1)−2(y+3)3(2y−1)−5y=2(y+1)−2(y+3)\) is \(y=−1\). |
Try It \(\PageIndex{23}\)
Solve: \(4(2h−3)−7h=6(h−2)−6(h−1)\).
- Answer
-
\(h = 6\)
Try It \(\PageIndex{24}\)
Solve: \(2(5x+2)−9x=3(x−2)−3(x−4)\).
- Answer
-
\(x=2\)
Translate to an Equation and Solve
To solve applications algebraically, we will begin by translating from English sentences into equations. Our first step is to look for the word (or words) that would translate to the equals sign. Here are some of the words that are commonly used.
Equals =
- is
- is equal to
- is the same as
- the result is
- gives
- was
- will be
The steps we use to translate a sentence into an equation are listed below.
TRANSLATE AN ENGLISH SENTENCE TO AN ALGEBRAIC EQUATION
- Locate the “equals” word(s). Translate to an equals sign (=).
- Translate the words to the left of the “equals” word(s) into an algebraic expression.
- Translate the words to the right of the “equals” word(s) into an algebraic expression.
Example \(\PageIndex{25}\)
Translate and solve: Eleven more than x is equal to 54.
Solution
| Translate. | 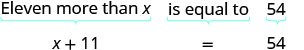 |
| Subtract 11 from both sides. |  |
| Simplify. |  |
| Check: Is 54 eleven more than 43? \[\begin{array} {rrr} {43 + 11} &{\stackrel{?}{=}} &{54}\\ {54} &{=} &{54\checkmark} \end{array}\] |
Try It \(\PageIndex{26}\)
Translate and solve: Ten more than x is equal to 41.
- Answer
-
\(x+10=41;x=31\)
Try It \(\PageIndex{27}\)
Translate and solve: Twelve less than x is equal to 51.
- Answer
-
y−12=51;y=63
Example \(\PageIndex{28}\)
Translate and solve: The difference of 12t and 11t is −14.
Solution
| Translate. | 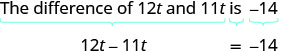 |
| Simplify. |  |
| Check: \[\begin{array} {rrl} {12(-14) - 11(-14)} &{\stackrel{?}{=}} &{-14}\\{-168 + 154} &{\stackrel{?}{=}} &{-14} \\ {-14} &{=} &{-14\checkmark}\end{array}\] |
Try It \(\PageIndex{29}\)
Translate and solve: The difference of 4x and 3x is 14.
- Answer
-
\(4x−3x=14;x=14\)
Try It \(\PageIndex{30}\)
Translate and solve: The difference of 7a and 6a is −8.
- Answer
-
\(7a−6a=−8;a=−8\)
Translate and Solve Applications
Most of the time a question that requires an algebraic solution comes out of a real life question. To begin with that question is asked in English (or the language of the person asking) and not in math symbols. Because of this, it is an important skill to be able to translate an everyday situation into algebraic language.
We will start by restating the problem in just one sentence, assign a variable, and then translate the sentence into an equation to solve. When assigning a variable, choose a letter that reminds you of what you are looking for. For example, you might use q for the number of quarters if you were solving a problem about coins.
Example \(\PageIndex{31}\): How to Solve Translate and Solve Applications
The MacIntyre family recycled newspapers for two months. The two months of newspapers weighed a total of 57 pounds. The second month, the newspapers weighed 28 pounds. How much did the newspapers weigh the first month?
Solution







Try It \(\PageIndex{32}\)
Translate into an algebraic equation and solve:
The Pappas family has two cats, Zeus and Athena. Together, they weigh 23 pounds. Zeus weighs 16 pounds. How much does Athena weigh?
- Answer
-
7 pounds
Try It \(\PageIndex{33}\)
Translate into an algebraic equation and solve:
Sam and Henry are roommates. Together, they have 68 books. Sam has 26 books. How many books does Henry have?
- Answer
-
42 books
SOLVE AN APPLICATION.
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
- Translate into an equation. It may be helpful to restate the problem in one sentence with the important information.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
Example \(\PageIndex{34}\)
Randell paid $28,675 for his new car. This was $875 less than the sticker price. What was the sticker price of the car?
Solution
\(\begin{array} {ll} {\textbf {Step 1. Read}\text{ the problem. }} &{}\\\\ {\textbf {Step 2. Identify}\text{ what we are looking for.}} &{\text{"What was the sticker price of the car?"}} \\\\ {\textbf{Step 3. Name}\text{ what we are looking for.}} &{} \\ {\text{Choose a variable to represent that quantity.}} &{\text{Let s = the sticker price of the car.}} \\\\{\textbf {Step 4. Translate}\text{ into an equation. Restate }} &{} \\ {\text{the problem in one sentence.}} &{$\text{28675 is } $\text{875 less than the sticker price}} \\ \\ {} &{$\text{28675 is } $\text{875 less than s}}\\ {}&{28675 = s - 875} \\ {\textbf {Step 5. Solve}\text{ the equation. }} &{28675 + 875 = s - 875 + 875}\\ {} &{29550 = s} \\ \\ {\textbf {Step 6. Check}\text{ the answer. }} &{} \\ {\text{Is }$875\text{ less than }$29550\text{ equal to } $28675?} &{} \\ {29550 - 875 \stackrel{?}{=} 28675} &{} \\ {28675 = 28675\checkmark} &{} \\ \\ {\textbf {Step 7. Answer}\text{ the question with }} &{\text{The sticker price of the car was }$29550.} \\ {\text{a complete sentence.}} &{} \end{array}\)
Try It \(\PageIndex{35}\)
Translate into an algebraic equation and solve:
Eddie paid $19875 for his new car. This was $1025 less than the sticker price. What was the sticker price of the car?
- Answer
-
$20900
Try It \(\PageIndex{36}\)
Translate into an algebraic equation and solve:
The admission price for the movies during the day is $7.75. This is $3.25 less the price at night. How much does the movie cost at night?
- Answer
-
$11.00
Key Concepts
- To Determine Whether a Number is a Solution to an Equation
- Substitute the number in for the variable in the equation.
- Simplify the expressions on both sides of the equation.
- Determine whether the resulting statement is true.
- If it is true, the number is a solution.
- If it is not true, the number is not a solution.
- Addition Property of Equality
- For any numbers a, b, and c, if a=b, then a+c=b+c.
- Subtraction Property of Equality
- For any numbers a, b, and c, if a=b, then a−c=b−c.
- To Translate a Sentence to an Equation
- Locate the “equals” word(s). Translate to an equal sign (=).
- Translate the words to the left of the “equals” word(s) into an algebraic expression.
- Translate the words to the right of the “equals” word(s) into an algebraic expression.
- To Solve an Application
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
- Translate into an equation. It may be helpful to restate the problem in one sentence with the important information.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
Glossary
- solution of an equation
- A solution of an equation is a value of a variable that makes a true statement when substituted into the equation.