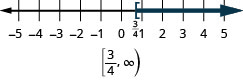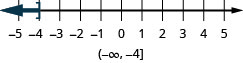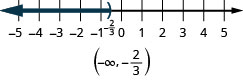2.7: Solve Linear Inequalities
- Last updated
- Save as PDF
- Page ID
- 18938
Learning Objectives
By the end of this section, you will be able to:
- Graph inequalities on the number line
- Solve inequalities using the Subtraction and Addition Properties of inequality
- Solve inequalities using the Division and Multiplication Properties of inequality
- Solve inequalities that require simplification
- Translate to an inequality and solve
Note
Before you get started, take this readiness quiz.
- Translate from algebra to English: \(15>x\).
If you missed this problem, review Exercise 1.3.1. - Solve: \(n−9=−42\).
If you missed this problem, review Exercise 2.1.7. - Solve: \(−5p=−23\).
If you missed this problem, review Exercise 2.2.1. - Solve: \(3a−12=7a−20\).
If you missed this problem, review Exercise 2.3.22.
Graph Inequalities on the Number Line
Do you remember what it means for a number to be a solution to an equation? A solution of an equation is a value of a variable that makes a true statement when substituted into the equation.
What about the solution of an inequality? What number would make the inequality \(x > 3\) true? Are you thinking, ‘x could be 4’? That’s correct, but x could be 5 too, or 20, or even 3.001. Any number greater than 3 is a solution to the inequality \(x > 3\).
We show the solutions to the inequality \(x > 3\) on the number line by shading in all the numbers to the right of 3, to show that all numbers greater than 3 are solutions. Because the number 3 itself is not a solution, we put an open parenthesis at 3. The graph of \(x > 3\) is shown in Figure \(\PageIndex{1}\). Please note that the following convention is used: light blue arrows point in the positive direction and dark blue arrows point in the negative direction.
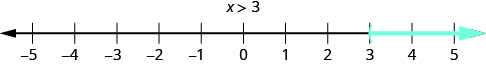
The graph of the inequality \(x \geq 3\) is very much like the graph of \(x > 3\), but now we need to show that 3 is a solution, too. We do that by putting a bracket at \(x = 3\), as shown in Figure \(\PageIndex{2}\).
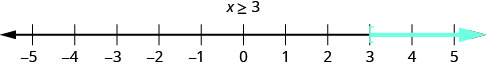
Notice that the open parentheses symbol, (, shows that the endpoint of the inequality is not included. The open bracket symbol, [, shows that the endpoint is included.
Exercise \(\PageIndex{1}\)
Graph on the number line:
- \(x\leq 1\)
- \(x<5\)
- \(x>−1\)
- Answer
-
1. \(x\leq 1\) This means all numbers less than or equal to 1. We shade in all the numbers on the number line to the left of 1 and put a bracket at x=1 to show that it is included.
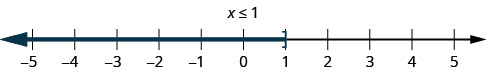
2. \(x<5\) This means all numbers less than 5, but not including 5. We shade in all the numbers on the number line to the left of 5 and put a parenthesis at x=5 to show it is not included.
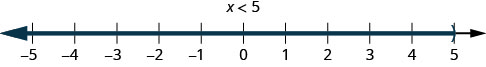
3. \(x>−1\) This means all numbers greater than −1, but not including −1. We shade in all the numbers on the number line to the right of −1, then put a parenthesis at x=−1 to show it is not included.
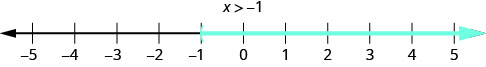
Exercise \(\PageIndex{2}\)
Graph on the number line:
- \(x\leq −1\)
- \(x>2\)
- \(x<3\)
- Answer
-
Exercise \(\PageIndex{3}\)
Graph on the number line:
- \(x>−2\)
- \(x<−3\)
- \(x\geq −1\)
- Answer
-
We can also represent inequalities using interval notation. As we saw above, the inequality \(x>3\) means all numbers greater than 3. There is no upper end to the solution to this inequality. In interval notation, we express \(x>3\) as \((3, \infty)\). The symbol \(\infty\) is read as ‘infinity’. It is not an actual number. Figure \(\PageIndex{3}\) shows both the number line and the interval notation.

The inequality \(x\leq 1\) means all numbers less than or equal to 1. There is no lower end to those numbers. We write \(x\leq 1\) in interval notation as \((-\infty, 1]\). The symbol \(-\infty\) is read as ‘negative infinity’. Figure \(\PageIndex{4}\) shows both the number line and interval notation.

INEQUALITIES, NUMBER LINES, AND INTERVAL NOTATION

Did you notice how the parenthesis or bracket in the interval notation matches the symbol at the endpoint of the arrow? These relationships are shown in Figure \(\PageIndex{5}\).

Exercise \(\PageIndex{4}\)
Graph on the number line and write in interval notation.
- \(x \geq -3\)
- \(x<2.5\)
- \(x\leq \frac{3}{5}\)
- Answer
-
1.
2.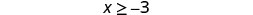
Shade to the right of −3, and put a bracket at −3. 
Write in interval notation. 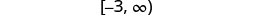
3.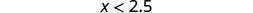
Shade to the left of 2.5, and put a parenthesis at 2.5. 
Write in interval notation. 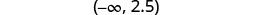
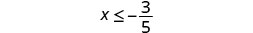
Shade to the left of \(-\frac{3}{5}\), and put a bracket at \(-\frac{3}{5}\). 
Write in interval notation. 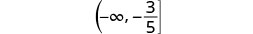
Exercise \(\PageIndex{5}\)
Graph on the number line and write in interval notation:
- \(x>2\)
- \(x\leq −1.5\)
- \(x\geq \frac{3}{4}\)
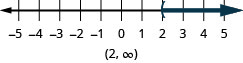
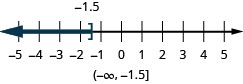
- Answer
-
Exercise \(\PageIndex{6}\)
Graph on the number line and write in interval notation:
- \(x\leq −4\)
- \(x\geq 0.5\)
- \(x<-\frac{2}{3}\)
- Answer
-
Solve Inequalities using the Subtraction and Addition Properties of Inequality
The Subtraction and Addition Properties of Equality state that if two quantities are equal, when we add or subtract the same amount from both quantities, the results will be equal.
PROPERTIES OF EQUALITY
\[\begin{array} { l l } { \textbf { Subtraction Property of Equality } } & { \textbf { Addition Property of Equality } } \\ { \text { For any numbers } a , b , \text { and } c , } & { \text { For any numbers } a , b , \text { and } c } \\ { \text { if } \qquad \quad a = b , } & { \text { if } \qquad \quad a = b } \\ { \text { then } a - c = b - c . } & { \text { then } a + c = b + c } \end{array}\]
Similar properties hold true for inequalities.
| For example, we know that −4 is less than 2. | 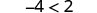 |
| If we subtract 5 from both quantities, is the left side still less than the right side? | 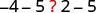 |
| We get −9 on the left and −3 on the right. |  |
| And we know −9 is less than −3. |  |
|
The inequality sign stayed the same. |
Similarly we could show that the inequality also stays the same for addition.
This leads us to the Subtraction and Addition Properties of Inequality.
PROPERTIES OF INEQUALITY
\[\begin{array} { l l } { \textbf { Subtraction Property of Inequality } } & { \textbf { Addition Property of Inequality } } \\ { \text { For any numbers } a , b , \text { and } c , } & { \text { For any numbers } a , b , \text { and } c } \\ { \text { if }\qquad \quad a < b } & { \text { if } \qquad \quad a < b } \\ { \text { then } a - c < b - c . } & { \text { then } a + c < b + c } \\\\ { \text { if } \qquad \quad a > b } & { \text { if } \qquad \quad a > b } \\ { \text { then } a - c > b - c . } & { \text { then } a + c > b + c } \end{array}\]
We use these properties to solve inequalities, taking the same steps we used to solve equations. Solving the inequality \(x+5>9\), the steps would look like this:
\[\begin{array}{rrll} {} &{x + 5} &{ >} &{9} \\ {\text{Subtract 5 from both sides to isolate }x.} &{x + 5 - 5} &{ >} &{9 - 5} \\{} &{x} &{ >} &{4} \\ \end{array}\]
Any number greater than 4 is a solution to this inequality.
Exercise \(\PageIndex{7}\)
Solve the inequality \(n - \frac{1}{2} \leq \frac{5}{8}\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
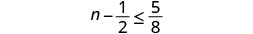
Add \(\frac{1}{2}\) to both sides of the inequality. 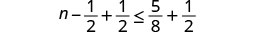
Simplify. 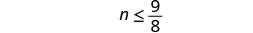
Graph the solution on the number line. 
Write the solution in interval notation.
Exercise \(\PageIndex{8}\)
Solve the inequality, graph the solution on the number line, and write the solution in interval notation.
\(p - \frac{3}{4} \geq \frac{1}{6}\)
- Answer
-
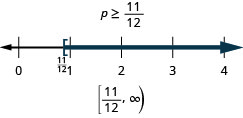
Exercise \(\PageIndex{9}\)
Solve the inequality, graph the solution on the number line, and write the solution in interval notation.
\(r - \frac{1}{3} \leq \frac{7}{12}\)
- Answer
-
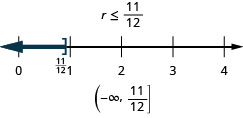
Solve Inequalities using the Division and Multiplication Properties of Inequality
The Division and Multiplication Properties of Equality state that if two quantities are equal, when we divide or multiply both quantities by the same amount, the results will also be equal (provided we don’t divide by 0).
PROPERTIES OF EQUALITY
\[\begin{array}{ll} {\textbf{Division Property of Equality}} &{\textbf{MUltiplication Property of Equality}} \\ {\text{For any numbers a, b, c, and c} \neq 0} &{\text{For any numbers a, b, c}} \\ {\text{if } \qquad a = b} &{\text{if} \qquad \quad a = b} \\ {\text{then }\quad \frac{a}{c} = \frac{b}{c}} &{\text{then } \quad ac = bc} \end{array}\]
Are there similar properties for inequalities? What happens to an inequality when we divide or multiply both sides by a constant?
Consider some numerical examples.
 |
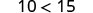 |
||
| Divide both sides by 5. | 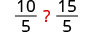 |
Multiply both sides by 5. |  |
| Simplify. |  |
 |
|
| Fill in the inequality signs. |  |
 |
The inequality signs stayed the same.
Does the inequality stay the same when we divide or multiply by a negative number?
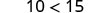 |
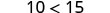 |
||
| Divide both sides by -5. | 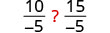 |
Multiply both sides by -5. |  |
| Simplify. |  |
 |
|
| Fill in the inequality signs. |  |
 |
The inequality signs reversed their direction.
When we divide or multiply an inequality by a positive number, the inequality sign stays the same. When we divide or multiply an inequality by a negative number, the inequality sign reverses.
Here are the Division and Multiplication Properties of Inequality for easy reference.
DIVISION AND MULTIPLICATION PROPERTIES OF INEQUALITY
For any real numbers a,b,c
\[\begin{array}{ll} {\text{if } a < b \text{ and } c > 0, \text{ then}} &{\frac{a}{c} < \frac{b}{c} \text{ and } ac < bc} \\ {\text{if } a > b \text{ and } c > 0, \text{ then}} &{\frac{a}{c} > \frac{b}{c} \text{ and } ac > bc} \\ {\text{if } a < b \text{ and } c < 0, \text{ then}} &{\frac{a}{c} > \frac{b}{c} \text{ and } ac > bc} \\ {\text{if } a > b \text{ and } c < 0, \text{ then}} &{\frac{a}{c} < \frac{b}{c} \text{ and } ac < bc} \end{array}\]
When we divide or multiply an inequality by a:
- positive number, the inequality stays the same.
- negative number, the inequality reverses.
Exercise \(\PageIndex{10}\)
Solve the inequality \(7y<42\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
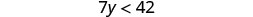
Divide both sides of the inequality by 7.
Since \(7>0\), the inequality stays the same.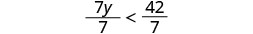
Simplify. 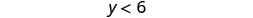
Graph the solution on the number line. 
Write the solution in interval notation. 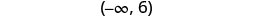
Exercise \(\PageIndex{11}\)
Solve the inequality, graph the solution on the number line, and write the solution in interval notation.
\(9c>72\)
- Answer
-
\(c>8\)

\((8, \infty)\)
Exercise \(\PageIndex{12}\)
Solve the inequality, graph the solution on the number line, and write the solution in interval notation.
\(12d\leq 60\)
- Answer
-
\(d\leq 5\)

\((-\infty, 5]\)
Exercise \(\PageIndex{13}\)
Solve the inequality \(−10a\geq 50\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
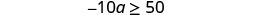
Divide both sides of the inequality by −10.
Since \(−10<0\), the inequality reverses.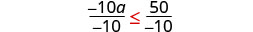
Simplify. 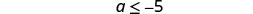
Graph the solution on the number line. 
Write the solution in interval notation. 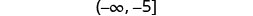
Exercise \(\PageIndex{14}\)
Solve each inequality, graph the solution on the number line, and write the solution in interval notation.
\(−8q<32\)
- Answer
-
\(q>−4\)
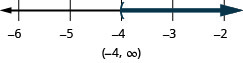
Exercise \(\PageIndex{15}\)
Solve each inequality, graph the solution on the number line, and write the solution in interval notation.
\(−7r\leq −70\)
- Answer
-
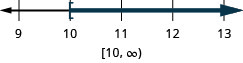
SOLVING INEQUALITIES
Sometimes when solving an inequality, the variable ends up on the right. We can rewrite the inequality in reverse to get the variable to the left.\[\begin{array}{l} x > a\text{ has the same meaning as } a < x \end{array}\]
Think about it as “If Xavier is taller than Alex, then Alex is shorter than Xavier.”
Exercise \(\PageIndex{16}\)
Solve the inequality \(-20 < \frac{4}{5}u\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
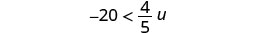
Multiply both sides of the inequality by \(\frac{5}{4}\).
Since \(\frac{5}{4} > 0\), the inequality stays the same.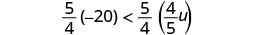
Simplify. 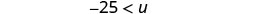
Rewrite the variable on the left. 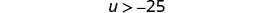
Graph the solution on the number line. 
Write the solution in interval notation. 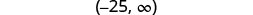
Exercise \(\PageIndex{17}\)
Solve the inequality, graph the solution on the number line, and write the solution in interval notation.
\(24 \leq \frac{3}{8}m\)
- Answer
-
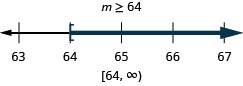
Exercise \(\PageIndex{18}\)
Solve the inequality, graph the solution on the number line, and write the solution in interval notation.
\(-24 < \frac{4}{3}n\)
- Answer
-
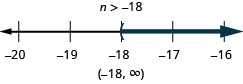
Exercise \(\PageIndex{19}\)
Solve the inequality \(\frac{t}{-2} \geq 8\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
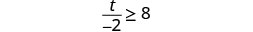
Multiply both sides of the inequality by −2.
Since \(−2<0\), the inequality reverses.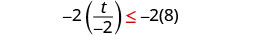
Simplify. 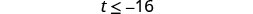
Graph the solution on the number line. 
Write the solution in interval notation. 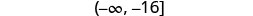
Exercise \(\PageIndex{20}\)
Solve the inequality, graph the solution on the number line, and write the solution in interval notation.
\(\frac{k}{-12}\leq 15\)
- Answer
-
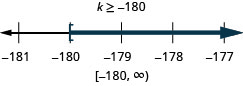
Exercise \(\PageIndex{21}\)
Solve the inequality, graph the solution on the number line, and write the solution in interval notation.
\(\frac{u}{-4}\geq -16\)
- Answer
-
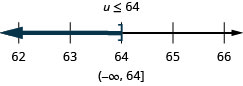
Solve Inequalities That Require Simplification
Most inequalities will take more than one step to solve. We follow the same steps we used in the general strategy for solving linear equations, but be sure to pay close attention during multiplication or division.
Exercise \(\PageIndex{22}\)
Solve the inequality \(4m\leq 9m+17\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
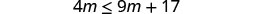
Subtract 9m from both sides to collect the variables on the left. 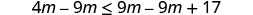
Simplify. 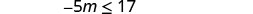
Divide both sides of the inequality by −5, and reverse the inequality. 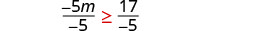
Simplify. 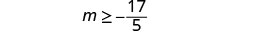
Graph the solution on the number line. 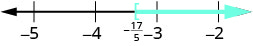
Write the solution in interval notation. 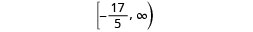
Exercise \(\PageIndex{23}\)
Solve the inequality \(3q\geq 7q−23\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
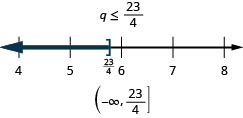
Exercise \(\PageIndex{24}\)
Solve the inequality \(6x<10x+19\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
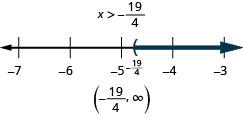
Exercise \(\PageIndex{25}\)
Solve the inequality \(8p+3(p−12)>7p−28\) graph the solution on the number line, and write the solution in interval notation.
- Answer
-
Simplify each side as much as possible. 8p+3(p−12)>7p−28 Distribute. 8p+3p−36>7p−28 Combine like terms. 11p−36>7p−28 Subtract 7p from both sides to collect the variables on the left. 11p−36−7p>7p−28−7p Simplify. 4p−36>−28 Add 36 to both sides to collect the constants on the right. 4p−36+36>−28+36 Simplify. 4p>8 Divide both sides of the inequality by 4; the inequality stays the same. \(\frac{4p}{4}>84\) Simplify. \(p>2\) Graph the solution on the number line. 
Write the solution in interval notation. \((2, \infty)\)
Exercise \(\PageIndex{26}\)
Solve the inequality \(9y+2(y+6)>5y−24\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
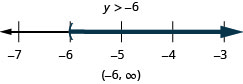
Exercise \(\PageIndex{27}\)
Solve the inequality \(6u+8(u−1)>10u+32\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
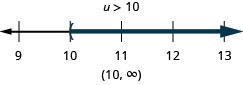
Just like some equations are identities and some are contradictions, inequalities may be identities or contradictions, too. We recognize these forms when we are left with only constants as we solve the inequality. If the result is a true statement, we have an identity. If the result is a false statement, we have a contradiction.
Exercise \(\PageIndex{28}\)
Solve the inequality \(8x−2(5−x)<4(x+9)+6x\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
Simplify each side as much as possible. 8x−2(5−x)<4(x+9)+6x Distribute. 8x−10+2x<4x+36+6x Combine like terms. 10x−10<10x+36 Subtract 10x from both sides to collect the variables on the left. 10x−10−10x<10x+36−10x Simplify. −10<36 The xx’s are gone, and we have a true statement. The inequality is an identity.
The solution is all real numbers.Graph the solution on the number line. 
Write the solution in interval notation. \((-\infty, \infty)\)
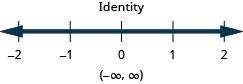
Exercise \(\PageIndex{29}\)
Solve the inequality \(4b−3(3−b)>5(b−6)+2b\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
Exercise \(\PageIndex{30}\)
Solve the inequality \(9h−7(2−h)<8(h+11)+8h\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
Exercise \(\PageIndex{31}\)
Solve the inequality \(\frac{1}{3}a - \frac{1}{8}a > \frac{5}{24}a + \frac{3}{4}\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
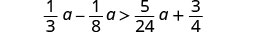
Multiply both sides by the LCD, 24, to clear the fractions. 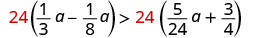
Simplify. 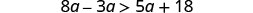
Combine like terms. 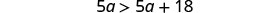
Subtract 5a from both sides to collect the variables on the left. 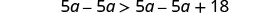
Simplify. 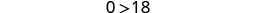
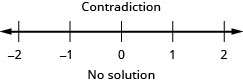
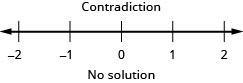
The statement is false! The inequality is a contradiction. There is no solution. Graph the solution on the number line. 
Write the solution in interval notation. There is no solution.
Exercise \(\PageIndex{32}\)
Solve the inequality \(\frac{1}{4}x - \frac{1}{12}x > \frac{1}{6}x + \frac{7}{8}\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
Exercise \(\PageIndex{33}\)
Solve the inequality \(\frac{2}{5}z - \frac{1}{3}z < \frac{1}{15}z - \frac{3}{5}\), graph the solution on the number line, and write the solution in interval notation.
- Answer
-
Translate to an Inequality and Solve
To translate English sentences into inequalities, we need to recognize the phrases that indicate the inequality. Some words are easy, like ‘more than’ and ‘less than’. But others are not as obvious.
Think about the phrase ‘at least’ – what does it mean to be ‘at least 21 years old’? It means 21 or more. The phrase ‘at least’ is the same as ‘greater than or equal to’.
Table \(\PageIndex{4}\) shows some common phrases that indicate inequalities.
| > | \(\geq\) | < | \(\leq\) |
|---|---|---|---|
| " data-valign="middle" class="lt-math-15134">is greater than | is greater than or equal to | is less than | is less than or equal to |
| " data-valign="middle" class="lt-math-15134">is more than | is at least | is smaller than | is at most |
| " data-valign="middle" class="lt-math-15134">is larger than | is no less than | has fewer than | is no more than |
| " data-valign="middle" class="lt-math-15134">exceeds | is the minimum | is lower than | is the maximum |
Exercise \(\PageIndex{34}\)
Translate and solve. Then write the solution in interval notation and graph on the number line.
Twelve times c is no more than 96.
- Answer
-
Translate. 
Solve—divide both sides by 12. 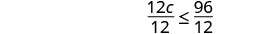
Simplify. 
Write in interval notation. 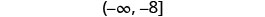
Graph on the number line. 
Exercise \(\PageIndex{35}\)
Translate and solve. Then write the solution in interval notation and graph on the number line.
Twenty times y is at most 100
- Answer
-
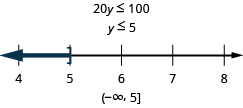
Exercise \(\PageIndex{36}\)
Translate and solve. Then write the solution in interval notation and graph on the number line.
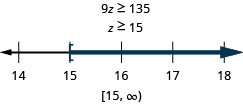
Nine times z is no less than 135
- Answer
-
Exercise \(\PageIndex{37}\)
Translate and solve. Then write the solution in interval notation and graph on the number line.
Thirty less than x is at least 45.
- Answer
-
Translate. 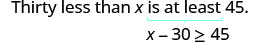
Solve—add 30 to both sides. 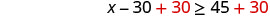
Simplify. 
Write in interval notation. 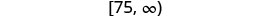
Graph on the number line. 
Exercise \(\PageIndex{38}\)
Translate and solve. Then write the solution in interval notation and graph on the number line.
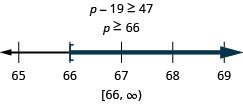
Nineteen less than p is no less than 47
- Answer
-
Exercise \(\PageIndex{39}\)
Translate and solve. Then write the solution in interval notation and graph on the number line.
Four more than a is at most 15.
- Answer
-
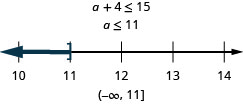
Key Concepts
- Subtraction Property of Inequality
For any numbers a, b, and c,
if a<b then a−c<b−c and
if a>b then a−c>b−c. - Addition Property of Inequality
For any numbers a, b, and c,
if a<b then a+c<b+c and
if a>b then a+c>b+c. - Division and Multiplication Properties of Inequality
For any numbers a, b, and c,
if a<b and c>0, then ac<bc and ac>bc.
if a>b and c>0, then ac>bc and ac>bc.
if a<b and c<0, then ac>bc and ac>bc.
if a>b and c<0, then ac<bc and ac<bc. - When we divide or multiply an inequality by a:
- positive number, the inequality stays the same.
- negative number, the inequality reverses.