10.4: Solve Applications Modeled by Quadratic Equations
- Last updated
- Save as PDF
- Page ID
- 18999
Learning Objectives
By the end of this section, you will be able to:
- Solve applications modeled by Quadratic Equations
Be Prepared
Before you get started, take this readiness quiz.
- The sum of two consecutive odd numbers is −100. Find the numbers.
If you missed this problem, review [link]. - The area of triangular mural is 64 square feet. The base is 16 feet. Find the height.
If you missed this problem, review [link]. - Find the length of the hypotenuse of a right triangle with legs 5 inches and 12 inches.
If you missed this problem, review [link].
Solve Applications of the Quadratic Formula
We solved some applications that are modeled by quadratic equations earlier, when the only method we had to solve them was factoring. Now that we have more methods to solve quadratic equations, we will take another look at applications. To get us started, we will copy our usual Problem Solving Strategy here so we can follow the steps.
Definition: USE THE PROBLEM SOLVING STRATEGY
- Read the problem. Make sure all the words and ideas are understood.
- Identify what we are looking for.
- Name what we are looking for. Choose a variable to represent that quantity.
- Translate into an equation. It may be helpful to restate the problem in one sentence with all the important information. Then, translate the English sentence into an algebra equation.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
We have solved number applications that involved consecutive even integers and consecutive odd integers by modeling the situation with linear equations. Remember, we noticed each even integer is 2 more than the number preceding it. If we call the first one n, then the next one is \(n+2\). The next one would be \(n+2+2\) or \(n+4\). This is also true when we use odd integers. One set of even integers and one set of odd integers are shown below.
\[\begin{array}{cccc} {}&{\textbf{Consecutive even integers}}&{}&{\textbf{Consecutive odd integers}}\\ {}&{64, 66, 68}&{}&{77, 79, 81}\\ {n}&{1^{st} \text{even number}}&{n}&{1^{st} \text{odd number}}\\ {n+2}&{2^{nd} \text{even number}} &{n+2}&{2^{nd} \text{odd number}}\\ {n+4}&{3^{rd} \text{even number}}&{n+4}&{3^{rd} \text{odd number}}\\ \end{array}\]
Some applications of consecutive odd integers or consecutive even integers are modeled by quadratic equations. The notation above will be helpful as you name the variables.
Example \(\PageIndex{1}\)
The product of two consecutive odd integers is 195. Find the integers.
- Answer
-
Step 1. Read the problem. Step 2. Identify what we are looking for. We are looking for two consecutive odd integers. Step 3. Name what we are looking for. Let \(n=\) the first odd integer.
\(n+2=\) the next odd integerStep 4. Translate into an equation. State the problem in one sentence. "The product of two consecutive odd integers is 195." The product of the first odd integer and the second odd integer is 195. Translate into an equation. 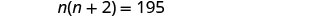
Step 5. Solve the equation. Distribute. 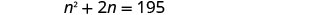
Subtract 195 to get the equation in standard form. 
Identify the a, b, c values. 
Write the quadratic equation. 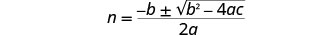
Then substitute in the values of a, b, c.. 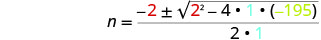
Simplify. 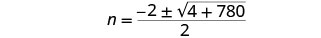
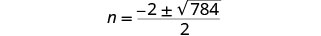
Simplify the radical. 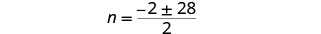
Rewrite to show two solutions. 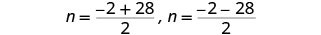
Solve each equation. 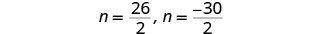
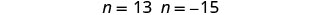
There are two values of n that are solutions. This will give us two pairs of consecutive odd integers for our solution. First odd integer n=13
next odd integer n+2
13+2
15First odd integer n=−15
next odd integer n+2
−15+2
−13Step 6. Check the answer.
Do these pairs work?
Are they consecutive odd integers?
Is their product 195?13, 15, yes −13, −15, yes
13⋅15=195, yes −13(−15)=195, yes
Step 7. Answer the question. The two consecutive odd integers whose product is 195 are 13, 15, and −13, −15.
Example \(\PageIndex{2}\)
The product of two consecutive odd integers is 99. Find the integers.
- Answer
-
Two consecutive odd numbers whose product is 99 are 9 and 11, and −9 and −11.
Example \(\PageIndex{3}\)
The product of two consecutive odd integers is 168. Find the integers.
- Answer
-
Two consecutive even numbers whose product is 168 are 12 and 14,and −12 and −14.
We will use the formula for the area of a triangle to solve the next example.
Definition: AREA OF A TRIANGLE
For a triangle with base b and height h, the area, A, is given by the formula \(A=\frac{1}{2}bh\).
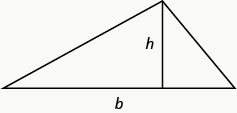
Recall that, when we solve geometry applications, it is helpful to draw the figure.
Example \(\PageIndex{4}\)
An architect is designing the entryway of a restaurant. She wants to put a triangular window above the doorway. Due to energy restrictions, the window can have an area of 120 square feet and the architect wants the width to be 4 feet more than twice the height. Find the height and width of the window.
- Answer
-
Step 1. Read the problem.
Draw a picture.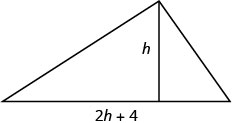
Step 2. Identify what we are looking for. We are looking for the height and width. Step 3. Name what we are looking for. Let \(h=\) the height of the triangle.
\(2h+4=\) the width of the triangleStep 4. Translate. We know the area. Write the formula for the area of a triangle.
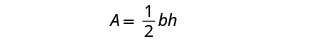
Step 5. Solve the equation. Substitute in the values. 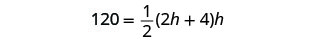
Distribute. 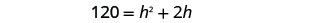
This is a quadratic equation, rewrite it in standard form. 
Solve the equation using the Quadratic Formula. Identify the a, b, c values. 
Write the quadratic equation. 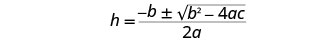
Then substitute in the values of a, b, c. 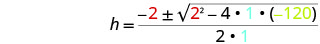
Simplify. 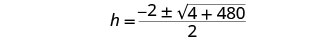
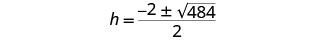
Simplify the radical. 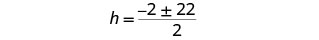
Rewrite to show two solutions. 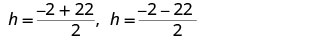
Simplify. 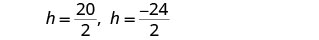
Since h is the height of a window, a value of \(h=−12\) does not make sense. 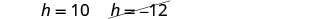
The height of the triangle: \(h=10\)
The width of the triangle: \(2h+4\)
\(2⋅10+4\)
\(24\)Step 6. Check the answer. Does a triangle with a height 10 and width 24 have area 120? Yes. Step 7. Answer the question. The height of the triangular window is 10 feet and the width is 24 feet. Notice that the solutions were integers. That tells us that we could have solved the equation by factoring.
When we wrote the equation in standard form, \(h^2+2h−120=0\), we could have factored it. If we did, we would have solved the equation \((h+12)(h−10)=0\).
Example \(\PageIndex{5}\)
Find the dimensions of a triangle whose width is four more than six times its height and has an area of 208 square inches.
- Answer
-
The height of the triangle is 8 inches and the width is 52 inches.
Example \(\PageIndex{6}\)
If a triangle that has an area of 110 square feet has a height that is two feet less than twice the width, what are its dimensions?
- Answer
-
The height of the triangle is 20 feet and the width is 11 feet.
In the two preceding examples, the number in the radical in the Quadratic Formula was a perfect square and so the solutions were rational numbers. If we get an irrational number as a solution to an application problem, we will use a calculator to get an approximate value.
The Pythagorean Theorem gives the relation between the legs and hypotenuse of a right triangle. We will use the Pythagorean Theorem to solve the next example.
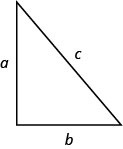
Definition: PYTHAGOREAN THEOREM
In any right triangle, where a and b are the lengths of the legs and c is the length of the hypotenuse, \(a^2+b^2=c^2\)
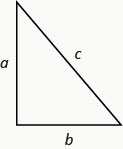
Example \(\PageIndex{7}\)
Rene is setting up a holiday light display. He wants to make a ‘tree’ in the shape of two right triangles, as shown below, and has two 10-foot strings of lights to use for the sides. He will attach the lights to the top of a pole and to two stakes on the ground. He wants the height of the pole to be the same as the distance from the base of the pole to each stake. How tall should the pole be?
- Answer
-
Step 1. Read the problem. Draw a picture 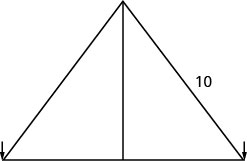
Step 2. Identify what we are looking for. We are looking for the height of the pole. Step 3. Name what we are looking for. The distance from the base of the pole to either stake is the same as the height of the pole. Let \(x=\) the height of the pole.
\(x=\) the distance from the pole to stakeEach side is a right triangle. We draw a picture of one of them. 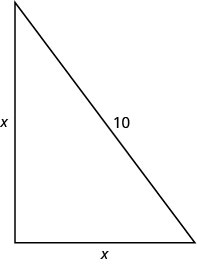
Step 4. Translate into an equation. We can use the Pythagorean Theorem to solve for x. Write the Pythagorean Theorem. \(a^2+b^2=c^2\) Step 5. Solve the equation. Substitute. \(x^2+x^2=10^2\) Simplify. \(2x^2=100\) Divide by 2 to isolate the variable. \(\frac{2x^2}{2}=\frac{100}{2}\) Simplify. \(x^2=50\) Use the Square Root Property. \(x=\pm\sqrt{50}\) Simplify the radical. \(x=\pm5\sqrt{2}\) Rewrite to show two solutions. \(x=5\sqrt{2}\)
\(\not{x=−5\sqrt{2}}\)Approximate this number to the nearest tenth with a calculator. \(x \approx 7.1\) Step 6. Check the answer.
Check on your own in the Pythagorean Theorem.Step 7. Answer the question. The pole should be about 7.1 feet tall.
Example \(\PageIndex{8}\)
The sun casts a shadow from a flag pole. The height of the flag pole is three times the length of its shadow. The distance between the end of the shadow and the top of the flag pole is 20 feet. Find the length of the shadow and the length of the flag pole. Round to the nearest tenth of a foot.
- Answer
-
The length of the shadow is 6.3 feet and the length of the flag pole is 18.9 ft.
Example \(\PageIndex{9}\)
The distance between opposite corners of a rectangular field is four more than the width of the field. The length of the field is twice its width. Find the distance between the opposite corners. Round to the nearest tenth.
- Answer
-
The distance to the opposite corner is 3.2.
Example \(\PageIndex{10}\)
Mike wants to put 150 square feet of artificial turf in his front yard. This is the maximum area of artificial turf allowed by his homeowners association. He wants to have a rectangular area of turf with length one foot less than three times the width. Find the length and width. Round to the nearest tenth of a foot.
- Answer
-
Step 1. Read the problem. Draw a picture. 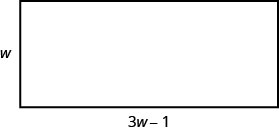
Step 2. Identify what we are looking for. We are looking for the length and width. Step 3. Name what we are looking for. Let \(w=\) the width of the rectangle.
\(3w−1=\) the length of the rectangleStep 4. Translate into an equation.
We know the area. Write the formula for the area of a rectangle.
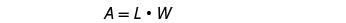
Step 5. Solve the equation. Substitute in the values. 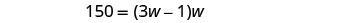
Distribute. 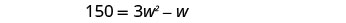
This is a quadratic equation, rewrite it in standard form. 
Solve the equation using the Quadratic Formula. Identify the a, b, c values. 
Write the Quadratic Formula. 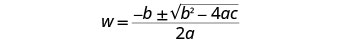
Then substitute in the values of a, b, c. 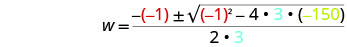
Simplify. 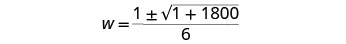
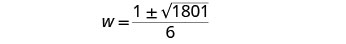
Rewrite to show two solutions. 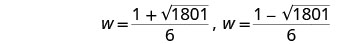
Approximate the answers using a calculator.
We eliminate the negative solution for the width.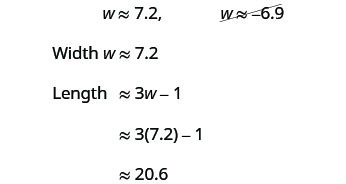
Step 6. Check the answer.
Make sure that the answers make sense.Step 7. Answer the question. The width of the rectangle is approximately 7.2 feet and the length 20.6 feet.
Example \(\PageIndex{11}\)
The length of a 200 square foot rectangular vegetable garden is four feet less than twice the width. Find the length and width of the garden. Round to the nearest tenth of a foot..
- Answer
-
The width of the garden is 11 feet and the length is 18 feet.
Example \(\PageIndex{12}\)
A rectangular tablecloth has an area of 80 square feet. The width is 5 feet shorter than the length. What are the length and width of the tablecloth? Round to the nearest tenth of a foot.
- Answer
-
The width of the tablecloth is 6.8 feet and the length is 11.8 feet.
The height of a projectile shot upwards is modeled by a quadratic equation. The initial velocity, \(v_{0}\), propels the object up until gravity causes the object to fall back down.
Definition: PROJECTILE MOTION
The height in feet, h, of an object shot upwards into the air with initial velocity, \(v_{0}\), after t seconds is given by the formula:
\(h=−16t^2+v_{0}t\)
We can use the formula for projectile motion to find how many seconds it will take for a firework to reach a specific height.
Example \(\PageIndex{13}\)
A firework is shot upwards with initial velocity 130 feet per second. How many seconds will it take to reach a height of 260 feet? Round to the nearest tenth of a second.
- Answer
-
Step 1. Read the problem. Step 2. Identify what we are looking for. We are looking for the number of seconds, which is time. Step 3. Name what we are looking for. Let \(t=\) the number of seconds. Step 4. Translate into an equation. Use the formula. \(h=−16t^2+v_{0}t\) Step 5. Solve the equation.
We know the velocity \(v_{0}\) is 130 feet per second.The height is 260 feet. Substitute the values. 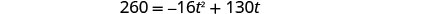
This is a quadratic equation, rewrite it in standard form. 
Solve the equation using the Quadratic Formula. Identify the a, b, c values. 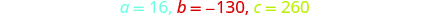
Write the Quadratic Formula. 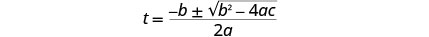
Then substitute in the values of a, b, c. 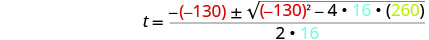
Simplify. 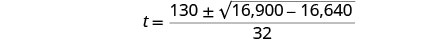
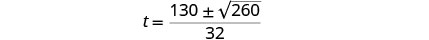
Rewrite to show two solutions. 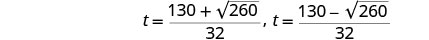
Approximate the answers with a calculator. \(t \approx 4.6\) seconds, \(t \approx 3.6\) Step 6. Check the answer.
The check is left to you.Step 7. Answer the question. The firework will go up and then fall back down.
As the firework goes up, it will reach 260 feet after
approximately 3.6 seconds. It will also pass that
height on the way down at 4.6 seconds.

Example \(\PageIndex{14}\)
An arrow is shot from the ground into the air at an initial speed of 108 ft/sec. Use the formula \(h=−16t^2+v_{0}t\) to determine when the arrow will be 180 feet from the ground. Round the nearest tenth of a second.
- Answer
-
The arrow will reach 180 on its way up in 3 seconds, and on the way down in 3.8 seconds.
Example \(\PageIndex{15}\)
A man throws a ball into the air with a velocity of 96 ft/sec. Use the formula \(h=−16t^2+v_{0}t\) to determine when the height of the ball will be 48 feet. Round to the nearest tenth of a second.
- Answer
-
The ball will reach 48 feet on its way up in .6 seconds and on the way down in 5.5 seconds.
Access these online resources for additional instruction and practice with solving word problems using the quadratic equation:
Key Concepts
- Area of a Triangle For a triangle with base, b, and height, h, the area, A, is given by the formula: \(A=\frac{1}{2}bh\)
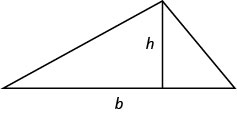
- Pythagorean Theorem In any right triangle, where a and b are the lengths of the legs, and c is the length of the hypothenuse, \(a^2+b^2=c^2\)
- Projectile motion The height in feet, h, of an object shot upwards into the air with initial velocity, \(v_{0}\), after tt seconds can be modeled by the formula
\(h=−16t^2+v_{0}t\)
Glossary
- consecutive even integers
- Consecutive even integers are even integers that follow right after one another. If an even integer is represented by n, the next consecutive even integer is \(n+2\), and the next after that is \(n+4\).
- consecutive odd integers
- Consecutive odd integers are odd integers that follow right after one another. If an odd integer is represented by n, the next consecutive odd integer is \(n+2\), and the next after that is \(n+4\).


