8.3: Operations on Radical Expressions

Last updated
Save as PDF

Page ID: 51481

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

Multiply and divide radical expressions
- Use properties of exponents to multiply and divide radical expressions
Add and subtract radical expressions
- Identify radicals that can be added or subtracted
- Add radical expressions
- Subtract radical expressions
Rationalize denominators
- Define irrational and rational denominators
- Remove radicals from a single term denominator

$Multiply and Divide$

Multiply and Divide

You can do more than just simplify radical expressions. You can multiply and divide them, too. Multiplying radicals is very simple if the index on all the radicals match. The prodcut rule of radicals can be generalized as follows

A Product Raised to a Power Rule

For any numbers a and b and any integer x: $(ab)^x= a^x \cdot b^x$
For any numbers a and b and any positive integer x: $ (ab)^{\frac{1}{x}}= a^{\frac{1}{x}} \cdot b^{\frac{1}{x}}$
For any numbers a and b and any positive integer x: $\sqrt[x]{ab}=\sqrt[x]{a}\cdot \sqrt[x]{b}$

The Product Raised to a Power Rule is important because you can use it to multiply radical expressions. Note that the roots are the same—you can combine square roots with square roots, or cube roots with cube roots, for example. But you can’t multiply a square root and a cube root using this rule.

In the following example, we multiply two square roots

Example

Simplify. $\sqrt{18}\cdot \sqrt{16}$

[reveal-answer q=”888021″]Show Solution[/reveal-answer]
[hidden-answer a=”888021″]Use the rule $\sqrt[x]{a}\cdot \sqrt[x]{b}=\sqrt[x]{ab}$ to multiply the radicands.

$\begin{array}{r}\sqrt{18\cdot 16}\\\\\sqrt{288}\end{array}$

Look for perfect squares in the radicand, and rewrite the radicand as the product of two factors.

$\sqrt{144\cdot 2}$

Identify perfect squares.

$\sqrt{{(12)^2}\cdot 2}$

Rewrite as the product of two radicals.

\(\sqrt

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[4]/p[9]/span, line 1, column 5

\cdot \sqrt{2}\)

Simplify, using \(\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[4]/p[10]/span, line 1, column 3

=\left| x \right|\).

$\begin{array}{r}\left| 12 \right|\cdot \sqrt{2}\\12\cdot \sqrt{2}\end{array}$

Answer

$\sqrt{18}\cdot \sqrt{16}=12\sqrt{2}$

[/hidden-answer]

Using the Product Raised to a Power Rule, you can take a seemingly complicated expression, $12\sqrt{2}$.

You may have also noticed that both $\sqrt{16}$ can be written as products involving perfect square factors. How would the expression change if you simplified each radical first, before multiplying?

Example

Simplify. $\sqrt{18}\cdot \sqrt{16}$

[reveal-answer q=”479810″]Show Solution[/reveal-answer]
[hidden-answer a=”479810″]Look for perfect squares in each radicand, and rewrite as the product of two factors.

$\begin{array}{r}\sqrt{9\cdot 2}\cdot \sqrt{4\cdot 4}\\\\\sqrt{3\cdot 3\cdot 2}\cdot \sqrt{4\cdot 4}\end{array}$

Identify perfect squares.

\(\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[5]/p[5]/span, line 1, column 5

Rewrite as the product of radicals.

\(\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[5]/p[7]/span[1], line 1, column 5

\cdot \sqrt{2}\cdot \sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[5]/p[7]/span[2], line 1, column 5

Simplify, using \(\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[5]/p[8]/span, line 1, column 3

=\left| x \right|\).

$\begin{array}{c}\left|3\right|\cdot\sqrt{2}\cdot\left|4\right|\\3\cdot\sqrt{2}\cdot4\end{array}$

Multiply.

$12$

Answer

$\sqrt{18}\cdot \sqrt{16}=12\sqrt{2}$

[/hidden-answer]

In both cases, you arrive at the same product, $12\sqrt{2}$. It does not matter whether you multiply the radicands or simplify each radical first.

You multiply radical expressions that contain variables in the same manner. As long as the roots of the radical expressions are the same, you can use the Product Raised to a Power Rule to multiply and simplify. Look at the two examples that follow. In both problems, the Product Raised to a Power Rule is used right away and then the expression is simplified.

Example

Simplify. $x\ge 0$

[reveal-answer q=”843487″]Show Solution[/reveal-answer]
[hidden-answer a=”843487″]Use the rule $\sqrt[x]{a}\cdot \sqrt[x]{b}=\sqrt[x]{ab}$ to multiply the radicands.

\(\sqrt{12

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[6]/p[3]/span[1], line 1, column 2

\cdot 3x}\\\\\sqrt{12\cdot 3\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[6]/p[3]/span[2], line 1, column 2

\cdot x}\)

Recall that \(

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[6]/p[4]/span[1], line 1, column 2

\cdot x=

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[6]/p[4]/span[2], line 1, column 2

\).

\(\begin{array}{r}\sqrt{36\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[6]/p[5]/span[1], line 1, column 2

}\\\\\sqrt{36\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[6]/p[5]/span[2], line 1, column 2

}\end{array}\)

Look for perfect squares in the radicand.

\(\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[6]/p[7]/span, line 1, column 5

Rewrite as the product of the result.

\(\begin{array}{c}\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[6]/p[9]/span[1], line 1, column 5

\cdot \sqrt

ParseError: "}" expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[6]/p[9]/span[2], line 1, column 4

\\6\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[6]/p[9]/span[3], line 1, column 2

\end{array}\)

Answer

\(\sqrt{12

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[6]/div/p[1]/span[1], line 1, column 2

}\cdot \sqrt{3x}=6

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[6]/div/p[1]/span[2], line 1, column 2

[/hidden-answer]

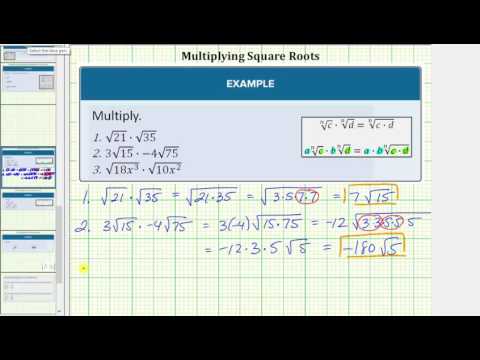
In this video example, we multiply more square roots with and without variables.

$Thumbnail for the embedded element "Multiply Square Roots"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=142

Example

Multiply $2\sqrt[3]{18}\cdot-7\sqrt[3]{15}$
[reveal-answer q=”852509″]Show Solution[/reveal-answer]
[hidden-answer a=”852509″]

Multiply the factors outside the radicals, and factor the radicands.

$-14\sqrt[3]{2\cdot3^2}\sqrt[3]{3\cdot5}$

Combine the radicands into one radical, and reorganize to see if there are any cubes.

$-14\sqrt[3]{2\cdot3^2\cdot3\cdot5}=-14\sqrt[3]{2\cdot3^3\cdot5}$

Apply the cube root to $3^3$, and simplify the radicand.

$-14\cdot3\sqrt[3]{2\cdot5}=-42\sqrt[3]{10}$

Answer

$2\sqrt[3]{18}\cdot-7\sqrt[3]{15}=-42\sqrt[3]{10}$

[/hidden-answer]

We will show one more example of multiplying cube root radicals, this time we will include a variable.

Example

Multiply $\sqrt[3]{4x^3}\cdot\sqrt[3]{2x^2}$
[reveal-answer q=”666812″]Show Solution[/reveal-answer]
[hidden-answer a=”666812″]

Factor the radicands, keeping in mind you want to find cubes.

$\sqrt[3]{4x^3}\cdot\sqrt[3]{2x^2}=\sqrt[3]{2^2\cdot{x^3}}\cdot\sqrt[3]{2x^2}$

Combine the radicands into one radical, and reorganize into cubes where possible.

$\begin{array}{c}\sqrt[3]{2^2\cdot{x^3}}\cdot\sqrt[3]{2x^2}\\\\=\sqrt[3]{2^2\cdot{x^3}\cdot2\cdot{x^2}}\\\\=\sqrt[3]{2^3\cdot{x^3}\cdot{x^2}}\end{array}$

Apply the cube root to $x^3$ and simplify the radicand.

$\sqrt[3]{2^3\cdot{x^3}\cdot{x^2}}=2\cdot{x}\sqrt[3]{x^2}$

Answer

$\sqrt[3]{4x^3}\cdot\sqrt[3]{2x^2}=2\cdot{x}\sqrt[3]{x^2}$

[/hidden-answer]

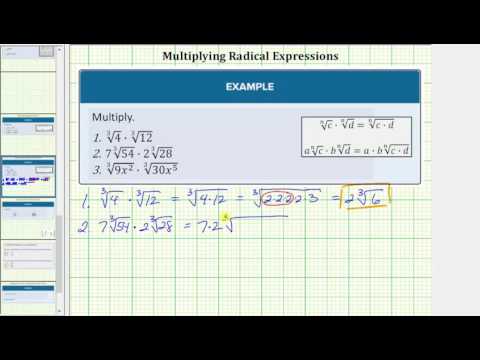
In the next video, we present more examples of multiplying cube roots.

$Thumbnail for the embedded element "Multiply Cube Roots"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=142

Dividing Radical Expressions

You can use the same ideas to help you figure out how to simplify and divide radical expressions. Recall that the Product Raised to a Power Rule states that $\sqrt[x]{ab}=\sqrt[x]{a}\cdot \sqrt[x]{b}$. Well, what if you are dealing with a quotient instead of a product?

There is a rule for that, too. The Quotient Raised to a Power Rule states that \(

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[7]/p[2]/span[1], line 1, column 1

=\frac

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[7]/p[2]/span[2], line 1, column 3

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[7]/p[2]/span[3], line 1, column 3

\). Again, if you imagine that the exponent is a rational number, then you can make this rule applicable for roots as well:

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[7]/p[3]/span[1], line 1, column 1

=\frac

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[7]/p[3]/span[2], line 1, column 3

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[7]/p[3]/span[3], line 1, column 3

Therefore

$\sqrt[x]{\frac{a}{b}}=\frac{\sqrt[x]{a}}{\sqrt[x]{b}}$.

A Quotient Raised to a Power Rule

For any real numbers a and b (b ≠ 0) and any positive integer x: \(

ParseError: invalid DekiScript (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[7]/div[1]/div/ul/li[1]/span[1], line 1, column 1

=\frac

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[7]/div[1]/div/ul/li[1]/span[2], line 1, column 3

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[7]/div[1]/div/ul/li[1]/span[3], line 1, column 3

For any real numbers a and b (b ≠ 0) and any positive integer x: $\sqrt[x]{\frac{a}{b}}=\frac{\sqrt[x]{a}}{\sqrt[x]{b}}$

As you did with multiplication, you will start with some examples featuring integers before moving on to radicals with variables.

Example

Simplify. $\sqrt{\frac{48}{25}}$

[reveal-answer q=”883744″]Show Solution[/reveal-answer]
[hidden-answer a=”883744″]Use the rule $\sqrt[x]{\frac{a}{b}}=\frac{\sqrt[x]{a}}{\sqrt[x]{b}}$ to create two radicals; one in the numerator and one in the denominator.

$\frac{\sqrt{48}}{\sqrt{25}}$

Simplify each radical. Look for perfect square factors in the radicand, and rewrite the radicand as a product of factors.

$\begin{array}{c}\frac{\sqrt{16\cdot 3}}{\sqrt{25}}\\\\\text{or}\\\\\frac{\sqrt{4\cdot 4\cdot 3}}{\sqrt{5\cdot 5}}\end{array}$

Identify and pull out perfect squares.

\(\begin{array}{r}\frac{\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[7]/div[2]/p[7]/span[1], line 1, column 5

{\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[7]/div[2]/p[7]/span[2], line 1, column 5

}\\\\\frac{\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[7]/div[2]/p[7]/span[3], line 1, column 5

\cdot \sqrt{3}}{\sqrt

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[7]/div[2]/p[7]/span[4], line 1, column 5

}\end{array}\)

Simplify.

$\frac{4\cdot \sqrt{3}}{5}$

Answer

$\sqrt{\frac{48}{25}}=\frac{4\sqrt{3}}{5}$

[/hidden-answer]

As with multiplication, the main idea here is that sometimes it makes sense to divide and then simplify, and other times it makes sense to simplify and then divide. Whichever order you choose, though, you should arrive at the same final expression.

Now let’s turn to some radical expressions containing variables. Notice that the process for dividing these is the same as it is for dividing integers.

Example

Simplify. $\frac{\sqrt{30x}}{\sqrt{10x}},x>0$

[reveal-answer q=”236188″]Show Solution[/reveal-answer]
[hidden-answer a=”236188″]Use the Quotient Raised to a Power Rule to rewrite this expression.

$\sqrt{\frac{30x}{10x}}$

Simplify $\sqrt{\frac{30x}{10x}}$ by identifying similar factors in the numerator and denominator and then identifying factors of 1.

$\begin{array}{r}\sqrt{\frac{3\cdot10x}{10x}}\\\\\sqrt{3\cdot\frac{10x}{10x}}\\\\\sqrt{3\cdot1}\end{array}$

Answer

$\frac{\sqrt{30x}}{\sqrt{10x}}=\sqrt{3}$

[/hidden-answer]

As you become more familiar with dividing and simplifying radical expressions, make sure you continue to pay attention to the roots of the radicals that you are dividing. For example, you can think of this expression:

\(\frac{\sqrt{8

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[7]/div[3]/div/p[4]/span[1], line 1, column 2

}}{\sqrt{225

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[7]/div[3]/div/p[4]/span[2], line 1, column 2

}}\)

As equivalent to:

\(\sqrt{\frac{8

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[7]/div[3]/div/p[6]/span[1], line 1, column 2

}{225

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[7]/div[3]/div/p[6]/span[2], line 1, column 2

}}\)

This is because both the numerator and the denominator are square roots.

Notice that you cannot express this expression:

\(\frac{\sqrt{8

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[7]/div[3]/div/p[9]/span[1], line 1, column 2

}}{\sqrt[4]{225

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[7]/div[3]/div/p[9]/span[2], line 1, column 2

}}\)

In this format:

\(\sqrt[4]{\frac{8

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[7]/div[3]/div/p[11]/span[1], line 1, column 2

}{225

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[7]/div[3]/div/p[11]/span[2], line 1, column 2

}}\).

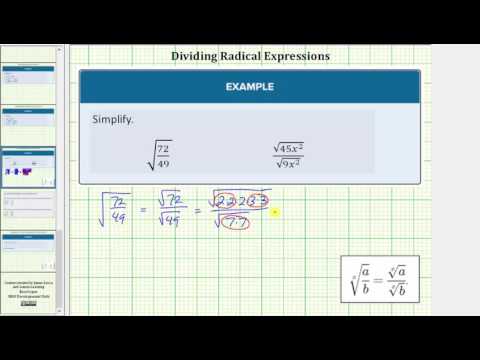
This is becuase the numerator is a square root and the denominator is a fourth root. In this last video, we show more examples of simplifying a quotient with radicals.

$Thumbnail for the embedded element "Simplify Basic Quotients of Square Roots"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=142

Add and Subtract Radical Expressions

Adding and subtracting radicals is much like combining like terms with variables. We can add and subtract expressions with variables like this:

$5x+3y - 4x+7y=x+10y$

There are two keys to combining radicals by addition or subtraction: look at the index, and look at the radicand. If these are the same, then addition and subtraction are possible. If not, then you cannot combine the two radicals.

$Three skeleton keys on a ring$

Keys

Remember the index is the degree of the root and the radicand is the term or expression under the radical. In the diagram below, the index is n, and the radicand is 100. The radicand is placed under the root symbol and the index is placed outside the root symbol to the left:

$nth root with 100 as the radicand and the word "radicand" below it has an arrow from it to the number 100, the word index points to the letter n which is in the position of the index of the root$

Index and radicand

Practice identifying radicals that are compatible for addition and subtraction by looking at the index and radicand of the roots in the following example.

Example

Identify the roots that have the same index and radicand.

$10\sqrt{6}$

$-1\sqrt[3]{6}$

$\sqrt{25}$

$12\sqrt{6}$

$\frac{1}{2}\sqrt[3]{25}$

$-7\sqrt[3]{6}$
[reveal-answer q=”332991″]Show Solution[/reveal-answer]
[hidden-answer a=”332991″]

Let’s start with $12\sqrt{6}$.

$-7\sqrt[3]{6}$.

$\sqrt{25}$ has an index of 2 and a radicand of 25. There are no other radicals in the list that have the same index and radicand.

$10\sqrt{6}$

$\frac{1}{2}\sqrt[3]{25}$ has an index of 3 and a radicand of 25. There are no other radicals in the list that share these.

$-1\sqrt[3]{6}$

[/hidden-answer]

Let’s use this concept to add some radicals.

Example

Add. $3a+7a$.

$\text{3}\sqrt{11}\text{ + 7}\sqrt{11}$

Answer

$3\sqrt{11}+7\sqrt{11}=10\sqrt{11}$

[/hidden-answer]

It may help to think of radical terms with words when you are adding and subtracting them. The last example could be read “three square roots of eleven plus 7 square roots of eleven”.

This next example contains more addends. Notice how you can combine like terms (radicals that have the same root and index) but you cannot combine unlike terms.

Example

Add. $5\sqrt{2}+\sqrt{3}+4\sqrt{3}+2\sqrt{2}$

[reveal-answer q=”687881″]Show Solution[/reveal-answer]
[hidden-answer a=”687881″]Rearrange terms so that like radicals are next to each other. Then add.

$5\sqrt{2}+2\sqrt{2}+\sqrt{3}+4\sqrt{3}$

Answer

$5\sqrt{2}+\sqrt{3}+4\sqrt{3}+2\sqrt{2}=7\sqrt{2}+5\sqrt{3}$

[/hidden-answer]

Notice that the expression in the previous example is simplified even though it has two terms: $5\sqrt{3}$. It would be a mistake to try to combine them further! (Some people make the mistake that $\sqrt{2}$ and $\sqrt{3}$ are not like radicals so they cannot be added.)

Example

Add. $3\sqrt{x}+12\sqrt[3]{xy}+\sqrt{x}$

[reveal-answer q=”885242″]Show Solution[/reveal-answer]
[hidden-answer a=”885242″]Rearrange terms so that like radicals are next to each other. Then add.

$3\sqrt{x}+\sqrt{x}+12\sqrt[3]{xy}$

Answer

$3\sqrt{x}+12\sqrt[3]{xy}+\sqrt{x}=4\sqrt{x}+12\sqrt[3]{xy}$

[/hidden-answer]

Sometimes you may need to add and simplify the radical. If the radicals are different, try simplifying first—you may end up being able to combine the radicals at the end, as shown in these next two examples.

Example

Add and simplify. $2\sqrt[3]{40}+\sqrt[3]{135}$

[reveal-answer q=”638886″]Show Solution[/reveal-answer]
[hidden-answer a=”638886″]Simplify each radical by identifying perfect cubes.

\(\begin{array}{r}2\sqrt[3]{8\cdot 5}+\sqrt[3]{27\cdot 5}\\2\sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[8]/div[7]/p[3]/span[1], line 1, column 5

\cdot \sqrt[3]{5}+\sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[8]/div[7]/p[3]/span[2], line 1, column 5

\cdot \sqrt[3]{5}\end{array}\)

Simplify.

$2\cdot 2\cdot \sqrt[3]{5}+3\cdot \sqrt[3]{5}$

Add.

$4\sqrt[3]{5}+3\sqrt[3]{5}$

Answer

$2\sqrt[3]{40}+\sqrt[3]{135}=7\sqrt[3]{5}$

[/hidden-answer]

Example

Add and simplify. \(x\sqrt[3]{x

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[8]/div[8]/p[1]/span, line 1, column 2

}+y\sqrt[3]{{{x}^{4}}y}\)

[reveal-answer q=”95976″]Show Solution[/reveal-answer]
[hidden-answer a=”95976″]Simplify each radical by identifying perfect cubes.

\(\begin{array}{r}x\sqrt[3]{x\cdot

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[8]/div[8]/p[3]/span[1], line 1, column 2

\cdot y}+y\sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[8]/div[8]/p[3]/span[2], line 1, column 3

\cdot \sqrt[3]{xy}+y\sqrt[3]

ParseError: colon expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[8]/div[8]/p[3]/span[3], line 1, column 3

\cdot \sqrt[3]{xy}\\xy\cdot \sqrt[3]{xy}+xy\cdot \sqrt[3]{xy}\end{array}\)

Add like radicals.

$xy\sqrt[3]{xy}+xy\sqrt[3]{xy}$

Answer

\(x\sqrt[3]{x

ParseError: EOF expected (click for details)

Callstack:
    at (Courses/Lumen_Learning/Beginning_Algebra_(Lumen)/08:_Roots_and_Rational_Exponents/8.03:_Operations_on_Radical_Expressions), /content/body/div[8]/div[8]/div/p[1]/span, line 1, column 2

}+y\sqrt[3]{{{x}^{4}}y}=2xy\sqrt[3]{xy}\)

[/hidden-answer]

Subtracting Radicals

Subtraction of radicals follows the same set of rules and approaches as addition—the radicands and the indices (plural of index) must be the same for two (or more) radicals to be subtracted.

Example

Subtract. $5\sqrt{13}-3\sqrt{13}$

[reveal-answer q=”107411″]Show Solution[/reveal-answer]
[hidden-answer a=”107411″]The radicands and indices are the same, so these two radicals can be combined.

$5\sqrt{13}-3\sqrt{13}$

Answer

$5\sqrt{13}-3\sqrt{13}=2\sqrt{13}$

[/hidden-answer]

Example

Subtract. $4\sqrt[3]{5a}-\sqrt[3]{3a}-2\sqrt[3]{5a}$

[reveal-answer q=”491962″]Show Solution[/reveal-answer]
[hidden-answer a=”491962″]Two of the radicals have the same index and radicand, so they can be combined. Rewrite the expression so that like radicals are next to each other.

$4\sqrt[3]{5a}-\sqrt[3]{3a}-2\sqrt[3]{5a}\\4\sqrt[3]{5a}-2\sqrt[3]{5a})-\sqrt[3]{3a})$

Combine. Although the indices of $-\sqrt[3]{3a}$ are the same, the radicands are not—so they cannot be combined.

$2\sqrt[3]{5a}-\sqrt[3]{3a})$

Answer

$4\sqrt[3]{5a}-\sqrt[3]{3a}-2\sqrt[3]{5a}=2\sqrt[3]{5a}-\sqrt[3]{3a}$

[/hidden-answer]

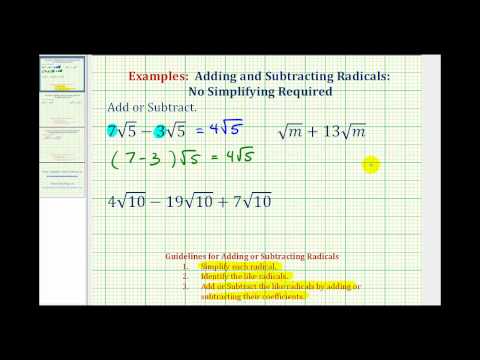
In the video example that follows, we show more examples of how to add and subtract radicals that don’t need to be simplified beforehand.

$Thumbnail for the embedded element "Ex: Add and Subtract Radicals - No Simplifying"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=142

The following video shows how to add and subtract radicals that can be simplified beforehand.

$Thumbnail for the embedded element "Ex: Add and Subtract Square Roots"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=142

Rationalize Denominators

Although radicals follow the same rules that integers do, it is often difficult to figure out the value of an expression containing radicals. For example, you probably have a good sense of how much $\frac{6}{9}$ are, but what about the quantities $\frac{1}{\sqrt{5}}$? These are much harder to visualize.

You can use a technique called rationalizing a denominator to eliminate the radical. The point of rationalizing a denominator is to make it easier to understand what the quantity really is by removing radicals from the denominators.

Recall that the numbers 5, $0.75$ are all known as rational numbers—they can each be expressed as a ratio of two integers ($\frac{3}{4}$ respectively). Some radicals are irrational numbers because they cannot be represented as a ratio of two integers. As a result, the point of rationalizing a denominator is to change the expression so that the denominator becomes a rational number.

Here are some examples of irrational and rational denominators.

Irrational		Rational
$\frac{\sqrt{2}}{2}$
$\frac{2\sqrt{3}+3}{3}$

Now let’s examine how to get from irrational to rational denominators.

Let’s start with the fraction $\sqrt{2}$, an irrational number. This makes it difficult to figure out what the value of $\frac{1}{\sqrt{2}}$ is.

You can rename this fraction without changing its value, if you multiply it by 1. In this case, set 1 equal to $\frac{\sqrt{2}}{\sqrt{2}}$. Watch what happens.

$\frac{1}{\sqrt{2}}\cdot 1=\frac{1}{\sqrt{2}}\cdot \frac{\sqrt{2}}{\sqrt{2}}=\frac{\sqrt{2}}{\sqrt{2\cdot 2}}=\frac{\sqrt{2}}{\sqrt{4}}=\frac{\sqrt{2}}{2}$

The denominator of the new fraction is no longer a radical (notice, however, that the numerator is).

So why choose to multiply $\frac{\sqrt{2}}{\sqrt{2}}$? You knew that the square root of a number times itself will be a whole number. In algebraic terms, this idea is represented by $\frac{1}{\sqrt{2}}\cdot 1$. Do you see where $\sqrt{2}\cdot \sqrt{2}=\sqrt{4}=2$?

Here are some more examples. Notice how the value of the fraction is not changed at all—it is simply being multiplied by 1.

Example

Rationalize the denominator.

$\frac{-6\sqrt{6}}{\sqrt{3}}$

[reveal-answer q=”551606″]Show Solution[/reveal-answer]
[hidden-answer a=”551606″]The denominator of this fraction is $\sqrt{3}$, since $\frac{\sqrt{3}}{\sqrt{3}}$ because it is equal to 1.

$\begin{array}{r}\frac{-6\sqrt{6}}{\sqrt{3}}\cdot \frac{\sqrt{3}}{\sqrt{3}}\\\\=\frac{-6\cdot\sqrt{6\cdot3}}{\sqrt{3\cdot3}}\\\\=\frac{-6\cdot\sqrt{6\cdot3}}{3}\end{array}$

Simplify the coefficients and the radicals, where possible.

$\begin{array}{c}\frac{-6\cdot\sqrt{6\cdot3}}{3}\\\\=-2\sqrt{3^2\cdot2}\\\\=-2\cdot3\sqrt{2}\\\\=-6\sqrt{2}\end{array}$

Answer

$\frac{-6\sqrt{6}}{\sqrt{3}}=-6\sqrt{2}$

[/hidden-answer]

In the video example that follows, we show more examples of how to rationalize a denominator with an integer radicand.

$Thumbnail for the embedded element "Ex 1: Rationalize the Denominator of a Radical Expression"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=142

You can use the same method to rationalize denominators to simplify fractions with radicals that contain a variable. As long as you multiply the original expression by another name for 1, you can eliminate a radical in the denominator without changing the value of the expression itself.

Example

Rationalize the denominator.

$\frac{\sqrt{2y}}{\sqrt{4x}},\text{ where }x\ne \text{0}$

[reveal-answer q=”642546″]Show Solution[/reveal-answer]
[hidden-answer a=”642546″]The denominator is $\frac{\sqrt{4x}}{\sqrt{4x}}$ to get rid of the radical in the denominator.

$\begin{array}{c}\frac{\sqrt{2y}}{\sqrt{4x}}\cdot \frac{\sqrt{4x}}{\sqrt{4x}}\\\\=\frac{\sqrt{2\cdot{y}\cdot{4}\cdot{x}}}{\sqrt{4^2\cdot{x^2}}}\\\\=\frac{\sqrt{2\cdot{2^2}\cdot{y}\cdot{x}}}{4|x|}\end{array}$

Simplify the numerator.

$\frac{2\sqrt{2\cdot{x}\cdot{y}}}{4|x|}\\\\=\frac{2\sqrt{2xy}}{4|x|}$

Answer

$\frac{\sqrt{2y}}{\sqrt{4x}}=\frac{2\sqrt{2xy}}{4|x|}$

[/hidden-answer]

Example

Rationalize the denominator and simplify.

$\sqrt{\frac{100x}{11y}},\text{ where }y\ne \text{0}$

[reveal-answer q=”197340″]Show Solution[/reveal-answer]
[hidden-answer a=”197340″]Rewrite $\frac{\sqrt{a}}{\sqrt{b}}$.

$\sqrt{\frac{100x}{11y}}=\frac{\sqrt{100x}}{\sqrt{11y}}$

The denominator is $\frac{\sqrt{11y}}{\sqrt{11y}}$ will rationalize the denominator.

$\frac{\sqrt{100x\cdot11y}}{\sqrt{11y}\cdot\sqrt{11y}}$

Multiply and simplify the radicals, where possible.

$\frac{\sqrt{100\cdot 11xy}}{\sqrt{11y}\cdot \sqrt{11y}}$

100 is a perfect square. Remember that$\sqrt{x}\cdot \sqrt{x}=x$.

$\frac{\sqrt{100}\cdot \sqrt{11xy}}{\sqrt{11y}\cdot \sqrt{11y}}$

Answer

$\sqrt{\frac{100x}{11y}}=\frac{10\sqrt{11xy}}{11|y|}$

[/hidden-answer]

THE video that follows shows more examples of how to rationalize a denominator with a monomial radicand.

$Thumbnail for the embedded element "Ex 2: Rationalize the Denominator of a Radical Expression"$

A YouTube element has been excluded from this version of the text. You can view it online here: pb.libretexts.org/ba/?p=142

Summary

When you encounter a fraction that contains a radical in the denominator, you can eliminate the radical by using a process called rationalizing the denominator. To rationalize a denominator, you need to find a quantity that, when multiplied by the denominator, will create a rational number (no radical terms) in the denominator. When the denominator contains a single term, as in $\frac{\sqrt{5}}{\sqrt{5}}$ will remove the radical from the denominator.

Summary

The Product Raised to a Power Rule and the Quotient Raised to a Power Rule can be used to simplify radical expressions as long as the roots of the radicals are the same. The Product Rule states that the product of two or more numbers raised to a power is equal to the product of each number raised to the same power. The same is true of roots:

\[\sqrt[x]{\frac{a}{b}}=\frac{\sqrt[x]{a}}{\sqrt[x]{b}}.\]

Combining radicals is possible when the index and the radicand of two or more radicals are the same. Radicals with the same index and radicand are known as like radicals. It is often helpful to treat radicals just as you would treat variables: like radicals can be added and subtracted in the same way that like variables can be added and subtracted. Sometimes, you will need to simplify a radical expression before it is possible to add or subtract like terms.

Contributors

Screenshot: Multiply and divide. Provided by: Lumen Learning. License: CC BY: Attribution
Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
Multiply Square Roots. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/PQs10_rFrSM. License: CC BY: Attribution
Multiple Cube Roots. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/cxRXofdelIM. License: CC BY: Attribution
Screenshot: keys. Provided by: Lumen Learning. License: CC BY: Attribution
Graphic: Index and radicand. Authored by: Lumen Learning. License: CC BY: Attribution

Unit 16: Radical Expressions and Quadratic Equations, from Developmental Math: An Open Program. Provided by: Monterey Institute of Technology and Education. Located at: http://nrocnetwork.org/resources/downloads/nroc-math-open-textbook-units-1-12-pdf-and-word-formats/. License: CC BY: Attribution
Ex: Add and Subtract Radicals - No Simplifying. Authored by: James Sousa (Mathispower4u.com) for Lumen Learning. Located at: https://youtu.be/5pVc44dEsTI. License: CC BY: Attribution
Ex: Add and Subtract Square Roots. Located at: https://youtu.be/tJk6_7lbrlw. License: CC BY: Attribution
Ex 1: Rationalize the Denominator of a Radical Expression. Authored by: James Sousa (Mathispower4u.com) . Located at: https://youtu.be/K7NdhPLVl7g. License: CC BY: Attribution
Ex 2: Rationalize the Denominator of a Radical Expression. Authored by: James Sousa (Mathispower4u.com). Located at: https://youtu.be/EBUzRctmgyk. License: CC BY: Attribution

Irrational		Rational
\(\frac{\sqrt{2}}{2}\)
\(\frac{2\sqrt{3}+3}{3}\)