28.2: D1.02- Examples 2–5
- Page ID
- 51776
Example 2
If we invest $750 at 6% annual interest, compounded quarterly, the formula for the amount A that the investment is worth after t years is . Find the amount the investment is worth after five years. Then evaluate this for several values of t between 0 and 30 years, and sketch a graph of this formula.
[reveal-answer q=”65508″]Show Answer[/reveal-answer]
[hidden-answer a=”65508″]
First, recall how to get an exponent in your calculator. On most calculators, it’s a ^ key or a
Callstack:
at (Courses/Lumen_Learning/Mathematics_for_the_Liberal_Arts_(Lumen)/28:_Topic_D-_FormulasComputing_and_Graphing/28.02:_D1.02-_Examples_25), /content/body/div[1]/div[1]/div/p[3]/img[1]/@alt, line 1, column 4
Callstack:
at (Courses/Lumen_Learning/Mathematics_for_the_Liberal_Arts_(Lumen)/28:_Topic_D-_FormulasComputing_and_Graphing/28.02:_D1.02-_Examples_25), /content/body/div[1]/div[1]/div/p[3]/img[2]/@alt, line 1, column 4
So the investment is worth $1010.14 after 5 years.
It is more convenient to be able to put all of these values into the calculator at the same time rather than writing intermediate steps. We will learn to do that in this course, but that’s not the point of this lesson. The point here is to practice making graphs. This will be useful to you in checking your work when you evaluate formulas. If one of the values you compute doesn’t seem to fit the pattern of the others, that warns you to check your computation again.
| Formula input and output | |
|---|---|
| t | A |
| 5 | 1010.141 |
| 0 | 750.000 |
| 10 | 1360.514 |
| 20 | 2467.997 |
| 30 | 4476.992 |
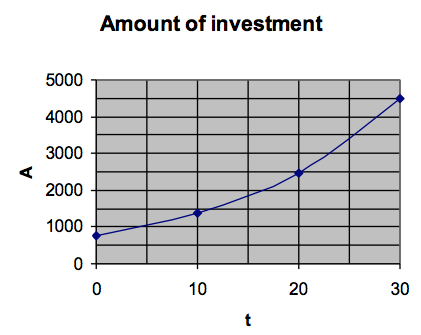 We can use the graph to estimate at what time the amount of the investment will be about $4000. Look at the graph to find 4000 on the vertical axis and then notice that the corresponding value on the horizontal axis is about 27.5. So at approximately 27.5 years, the amount of the investment will be $4000.
We can use the graph to estimate at what time the amount of the investment will be about $4000. Look at the graph to find 4000 on the vertical axis and then notice that the corresponding value on the horizontal axis is about 27.5. So at approximately 27.5 years, the amount of the investment will be $4000.
Check that by plugging it into the formula.
This is as close as we could reasonably expect from using a graph to approximate the input value.
[/hidden-answer]
Example 3
Consider our approximation from Example 2. We wanted to find the number of years to leave the money in so that the amount of the investment would be $4000. The graph suggested that years. But then we found that after 27.5 years, the amount was only $3857.68. Clearly we should leave the money in somewhat longer. How much longer?
[reveal-answer q=”137839″]Show Answer[/reveal-answer]
[hidden-answer a=”137839″]
If we know how to do some complicated algebra (using logarithms) we can quickly obtain an answer to “how long should we leave the money to earn $4000?” We will not do that particular type of algebra in this course. Instead we will use numerical work to get refine our estimate from the graph. Here, when we look at the graph and the numbers, it is clear that 30 years is too long and 27.5 years is too short. So we try some value in between. Let’s try 28 years. . This is much closer to the $4000 which was our goal. If we wanted to try to get it even more accurately, we would use a value larger than 28 years, but only very slightly larger. Since the amount is compounded quarterly, the next time the amount will increase is at 28.25 years, so let’s try that.
. That is further away from $4000 than the value for 28 years, so the best answer for this question is that the amount of the investment will be at about $4000 at 28 years.
[/hidden-answer]
Example 4
Following Example 2, we’d like to have a formula that allows us to vary the interest rate and number of times per year it is compounded as well as varying the number of years of the investment. So let r be the interest rate, converted to a decimal and n be the number of times per year it is compounded, and, as before t is the number of years and A is the amount of the investment. Then the formula is . This is an example of a formula with several input values. Use this formula to find the amount of the investment after 5 years if the interest rate is 8% and it is compounded monthly.
[reveal-answer q=”261282″]Show Answer[/reveal-answer]
[hidden-answer a=”261282″]
So after 5 years, this investment is worth $1117.38.
We can’t graph this easily, because we would need more than a two-dimensional graph. We need one dimension for the output value and one dimension for every input value and investigating four-dimensional graphs is beyond the scope of this course! However, in most practical applications, technicians and scientists isolate one or two input variables that they are most interested in and then analyze the problem with a two-dimensional graph (for one input variable) or a three-dimensional graph (for two input variables.) We will look at some three-dimensional graphs later in the course.
[/hidden-answer]
Example 5
Following Example 3, suppose we want to allow the initial amount of the investment to change. So we need a variable for that. Since it is an amount, we’d like to call it A, but we already have an A in this formula that means something else. We could use a different letter, but in applications problems we often choose to call both values A and distinguish between them by a subscript. In this problem, we would usually call the original amount of money
Callstack:
at (Courses/Lumen_Learning/Mathematics_for_the_Liberal_Arts_(Lumen)/28:_Topic_D-_FormulasComputing_and_Graphing/28.02:_D1.02-_Examples_25), /content/body/div[1]/div[4]/div/p[1]/img[1]/@alt, line 1, column 4
Callstack:
at (Courses/Lumen_Learning/Mathematics_for_the_Liberal_Arts_(Lumen)/28:_Topic_D-_FormulasComputing_and_Graphing/28.02:_D1.02-_Examples_25), /content/body/div[1]/div[4]/div/p[1]/img[2]/@alt, line 1, column 4
Callstack:
at (Courses/Lumen_Learning/Mathematics_for_the_Liberal_Arts_(Lumen)/28:_Topic_D-_FormulasComputing_and_Graphing/28.02:_D1.02-_Examples_25), /content/body/div[1]/div[4]/div/p[1]/img[3]/@alt, line 1, column 4
[reveal-answer q=”61734″]Show Answer[/reveal-answer]
[hidden-answer a=”61734″]
So, after 6 years, this investment is worth $1359.96.
[/hidden-answer]
- Mathematics for Measuring. Authored by: Mary Parker and Hunter Ellinger. License: CC BY: Attribution

