1.3: Solve a Formula for a Specific Variable
- Last updated
- Save as PDF
- Page ID
- 29037
Learning Objectives
By the end of this section, you will be able to:
- Solve a formula for a specific variable
- Use formulas to solve geometry applications
Before you get started, take this readiness quiz.
- Evaluate \(2(x+3)\) when \(x=5\).
If you missed this problem, review [link]. - The length of a rectangle is three less than the width. Let w represent the width. Write an expression for the length of the rectangle.
If you missed this problem, review [link]. - Evaluate \(\frac{1}{2}bh\) when \(b=14\) and \(h=9\).
If you missed this problem, review [link].
Solve a Formula for a Specific Variable
We have all probably worked with some geometric formulas in our study of mathematics. Formulas are used in so many fields, it is important to recognize formulas and be able to manipulate them easily.
It is often helpful to solve a formula for a specific variable. If you need to put a formula in a spreadsheet, it is not unusual to have to solve it for a specific variable first. We isolate that variable on one side of the equals sign with a coefficient of one and all other variables and constants are on the other side of the equal sign.
Geometric formulas often need to be solved for another variable, too. The formula \(V=\frac{1}{3}πr^2h\) is used to find the volume of a right circular cone when given the radius of the base and height. In the next example, we will solve this formula for the height.
EXAMPLE \(\PageIndex{1}\)
Solve the formula \(V=\frac{1}{3}πr^2h\) for h.
- Answer
-
Write the formula. 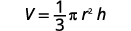
Remove the fraction on the right. 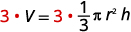
Simplify. 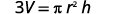
Divide both sides by \(πr^2\). 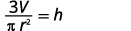
We could now use this formula to find the height of a right circular cone when we know the volume and the radius of the base, by using the formula \(h=\frac{3V}{πr^2}\).
EXAMPLE \(\PageIndex{2}\):
Use the formula \(A=\frac{1}{2}bh\) to solve for b.
- Answer
-
\(b=\frac{2A}{h}\)
EXAMPLE \(\PageIndex{3}\):
Use the formula \(A=\frac{1}{2}bh\) to solve for h.
- Answer
-
\(h=\frac{2A}{b}\)
In the sciences, we often need to change temperature from Fahrenheit to Celsius or vice versa. If you travel in a foreign country, you may want to change the Celsius temperature to the more familiar Fahrenheit temperature.
EXAMPLE \(\PageIndex{4}\)
Solve the formula \(C=\frac{5}{9}(F−32)\) for F.
- Answer
-
Write the formula. 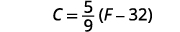
Remove the fraction on the right. 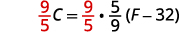
Simplify. 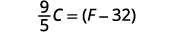
Add 32 to both sides. 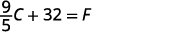
We can now use the formula \(F=\frac{9}{5}C+32\) to find the Fahrenheit temperature when we know the Celsius temperature.
EXAMPLE \(\PageIndex{5}\):
Solve the formula \(F=\frac{9}{5}C+32\) for C.
- Answer
-
\(C=\frac{5}{9}(F−32)\)
EXAMPLE \(\PageIndex{6}\):
Solve the formula \(A=\frac{1}{2}h(b+B)\) for b.
- Answer
-
\(b=\frac{2A−Bh}{h}\)
The next example uses the formula for the surface area of a right cylinder.
EXAMPLE \(\PageIndex{7}\)
Solve the formula \(S=2πr^2+2πrh\) for \(h\).
- Answer
-
Write the formula. 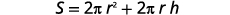
Isolate the \(h\) term by subtracting \(2πr^2\) from each side. 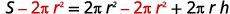
Simplify. 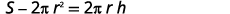
Solve for \(h\) by dividing both sides by \(2πr.\) 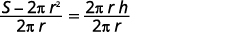
Simplify. 
EXAMPLE \(\PageIndex{8}\):
Solve the formula \(A=P+Prt\) for \(t\).
- Answer
-
\(t=\frac{A−P}{Pr}\)
EXAMPLE \(\PageIndex{9}\):
Solve the formula \(A=P+Prt\) for \(r\).
- Answer
-
\(r=\frac{A−P}{Pt}\)
Sometimes we might be given an equation that is solved for \(y\) and need to solve it for \(x\), or vice versa. In the following example, we’re given an equation with both \(x\) and \(y\) on the same side and we’ll solve it for \(y\).
Solve the formula \(8x+7y=15\) for \(y\).
- Answer
-
We will isolate \(y\) on one side of the equation. 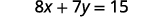
Subtract \(6x\) from both sides to isolate the term with \(y\). 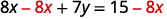
Simplify. 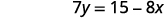
Divide both sides by \(7\) to make the coefficient of \(y\) one. 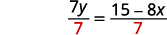
Simplify. 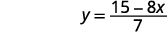
Solve the formula \(4x+7y=9\) for \(y\).
- Answer
-
\(y=\frac{9−4x}{7}\)
EXAMPLE \(\PageIndex{12}\)
Solve the formula \(5x+8y=1\) for \(y\).
- Answer
-
\(y=\frac{1−5x}{8}\)
Use Formulas to Solve Geometry Applications
In this objective we will use some common geometry formulas. We will adapt our problem solving strategy so that we can solve geometry applications. The geometry formula will name the variables and give us the equation to solve.
In addition, since these applications will all involve shapes of some sort, most people find it helpful to draw a figure and label it with the given information. We will include this in the first step of the problem solving strategy for geometry applications.
SOLVE GEOMETRY APPLICATIONS.
- Read the problem and make sure all the words and ideas are understood.
- Identify what you are looking for.
- Name what we are looking for by choosing a variable to represent it. Draw the figure and label it with the given information.
- Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
When we solve geometry applications, we often have to use some of the properties of the figures. We will review those properties as needed.
The next example involves the area of a triangle. The area of a triangle is one-half the base times the height. We can write this as \(A=\frac{1}{2}bh\), where \(b\) = length of the base and \(h\) = height.
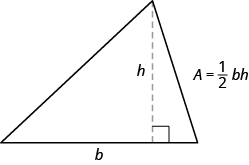
EXAMPLE \(\PageIndex{13}\)
The area of a triangular painting is \(126\) square inches. The base is \(18\) inches. What is the height?
- Answer
-
Step 1. Read the problem. Step 2. Identify what you are looking for. height of a triangle Step 3. Name. Choose a variable to represent it. Let \(h=\) the height. Draw the figure and label it with the given information. Area = 126 sq. in. 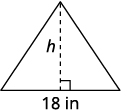
Step 4. Translate. Write the appropriate formula. \(A=\frac{1}{2}bh\) Substitute in the given information. \(126=\frac{1}{2}·18·h\) Step 5. Solve the equation. \(126=9h\) Divide both sides by 9. \(14=h\) Step 6. Check. \(\begin{align*} A &= \frac{1}{2}bh \\126 & \stackrel{?}{=} 12·18·14 \\ 126 &=126✓ \end{align*}\)
Step 7. Answer the question. The height of the triangle is \(14\) inches.
EXAMPLE \(\PageIndex{14}\):
The area of a triangular church window is \(90\) square meters. The base of the window is \(15\) meters. What is the window’s height?
- Answer
-
The window’s height is \(12\) meters.
EXAMPLE \(\PageIndex{15}\):
A triangular tent door has area \(15\) square feet. The height is five feet. What is the length of the base?
- Answer
-
The length of the base is \(6\) feet.
In the next example, we will work with a right triangle. To solve for the measure of each angle, we need to use two triangle properties. In any triangle, the sum of the measures of the angles is \(180°\). We can write this as a formula: \(m∠A+m∠B+m∠C=180\). Also, since the triangle is a right triangle, we remember that a right triangle has one \(90°\) angle.
Here, we will have to define one angle in terms of another. We will wait to draw the figure until we write expressions for all the angles we are looking for.
EXAMPLE \(\PageIndex{16}\):
The measure of one angle of a right triangle is 40 degrees more than the measure of the smallest angle. Find the measures of all three angles.
- Answer
-
Step 1. Read the problem. Step 2. Identify what you are looking for. the measures of all three angles Step 3. Name. Choose a variable to represent it. \(\begin{align*} \text{Let }a \; & = \; \mathrm{1^{st} \; angle.} \\ a+40 &= \mathrm{2^{nd} \; angle} \\90 &= \mathrm{3^{rd} \; angle \; (the \; right \; angle)} \end{align*}\) Draw the figure and label it with the given information. 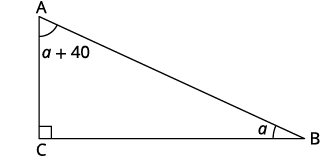
Step 4. Translate. Write the appropriate formula. 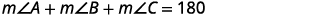
Substitute into the formula. 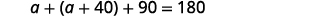.jpg?revision=1&size=bestfit&width=321&height=16)
Step 5. Solve the equation. 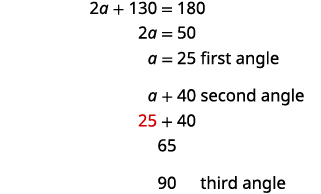
Step 6. Check. \( \begin{align*} 25+65+90 & \stackrel{?}{=} 180\\ 180 &= 180✓ \end{align*}\) Step 7. Answer the question. The three angles measure \(25°,\;65°\), and \(90°\).
EXAMPLE \(\PageIndex{17}\):
The measure of one angle of a right triangle is 50 more than the measure of the smallest angle. Find the measures of all three angles.
- Answer
-
The measures of the angles are \(20°, \;70°\), and \(90°\).
EXAMPLE \(\PageIndex{18}\):
The measure of one angle of a right triangle is \(30\) more than the measure of the smallest angle. Find the measures of all three angles.
- Answer
-
The measures of the angles are \(30°,\; 60°\), and \(90°\).
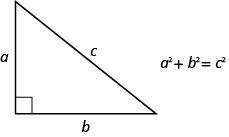
The next example uses another important geometry formula. The Pythagorean Theorem tells how the lengths of the three sides of a right triangle relate to each other. Writing the formula in every exercise and saying it aloud as you write it may help you memorize the Pythagorean Theorem.
THE PYTHAGOREAN THEOREM
In any right triangle, where a and b are the lengths of the legs, and c is the length of the hypotenuse, the sum of the squares of the lengths of the two legs equals the square of the length of the hypotenuse.
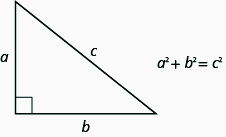
We will use the Pythagorean Theorem in the next example.
EXAMPLE \(\PageIndex{19}\):
Use the Pythagorean Theorem to find the length of the other leg in
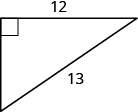
- Answer
-
Step 1. Read the problem. Step 2. Identify what you are looking for. the length of the leg of the triangle Step 3. Name. Choose a variable to represent it. Let \(a\) = the leg of the triangle. Label side a. 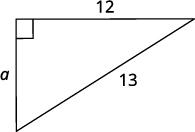
Step 4. Translate. Write the appropriate formula. Substitute. \(\begin{align*}a^2+b^2 &=c ^2 \\ a^2+12^2 &=13^2 \end{align*}\) Step 5. Solve the equation. Isolate the variable term. Use the definition of square root. Simplify. \(\begin{align*} a^2+144 &= 169 \\ a^2 &= 25 \\ a &= \sqrt{25} \\ a&=5 \end{align*}\) Step 6. Check. 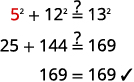
Step 7. Answer the question. The length of the leg is \(5\).
EXAMPLE \(\PageIndex{20}\):
Use the Pythagorean Theorem to find the length of the leg in the figure.
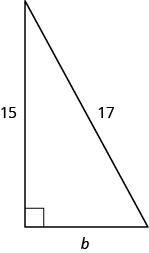
- Answer
-
The length of the leg is \(8\).
EXAMPLE \(\PageIndex{21}\):
Use the Pythagorean Theorem to find the length of the leg in the figure.
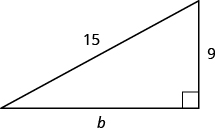
- Answer
-
The length of the leg is \(12\).
The next example is about the perimeter of a rectangle. Since the perimeter is just the distance around the rectangle, we find the sum of the lengths of its four sides—the sum of two lengths and two widths. We can write is as \(P=2L+2W\) where \(L\) is the length and \(W\) is the width. To solve the example, we will need to define the length in terms of the width.
EXAMPLE \(\PageIndex{22}\):
The length of a rectangle is six centimeters more than twice the width. The perimeter is \(96\) centimeters. Find the length and width.
- Answer
-
Step 1. Read the problem. Step 2. Identify what we are looking for. the length and the width Step 3. Name. Choose a variable to represent the width. The length is six more than twice the width. Let \(w=\) width. \(2w+6=\) length
\(P=96\) cm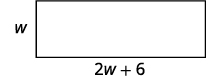
Step 4. Translate. Write the appropriate formula. 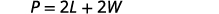
Substitute in the given information. 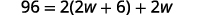
Step 5. Solve the equation. 
Step 6. Check.
\(\begin{align*} P &=2L+2W \\ 96 & \stackrel{?}{=}2·34+2·14 \\ 96 &=96✓ \end{align*}\)
Step 7. Answer the question. The length is \(34\) cm and the width is \(14\) cm
EXAMPLE \(\PageIndex{23}\):
The length of a rectangle is seven more than twice the width. The perimeter is \(110\) inches. Find the length and width.
- Answer
-
The length is \(16\) inches and the width is \(39\) inches.
EXAMPLE \(\PageIndex{24}\):
The width of a rectangle is eight yards less than twice the length. The perimeter is \(86\) yards. Find the length and width.
- Answer
-
The length is \(17\) yards and the width is \(26\) yards.
The next example is about the perimeter of a triangle. Since the perimeter is just the distance around the triangle, we find the sum of the lengths of its three sides. We can write this as \(P=a+b+c\), where \(a\), \(b\), and \(c\) are the lengths of the sides.
EXAMPLE \(\PageIndex{25}\):
One side of a triangle is three inches more than the first side. The third side is two inches more than twice the first. The perimeter is \(29\) inches. Find the length of the three sides of the triangle.
- Answer
-
Step 1. Read the problem. Step 2. Identify what we are looking for. the lengths of the three sides of a triangle Step 3. Name. Choose a variable to represent the length of the first side. \( \begin{align*} \mathrm{Let \;}x \;& \mathrm{= \; length \; of \;1^{st} \;side.} \\ x+3 \; &= \; \mathrm{length \; of \; 2^{nd} \; side} \\ 2x+2 \; &= \; \mathrm{length \; of \;3^{rd} \; side} \end{align*}\)
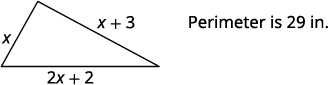
Step 4. Translate. Write the appropriate formula. Substitute in the given information. 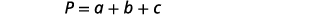
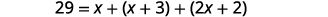
Step 5. Solve the equation. 
Step 6. Check.
\(\begin{align*} 29 & \stackrel{?}{=}6+9+14 \\ 29 &= 29✓ \end{align*}\)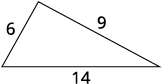
Step 7. Answer the question. The lengths of the sides of the triangle are \(6\), \(9\), and \(14\) inches.
EXAMPLE \(\PageIndex{26}\):
One side of a triangle is seven inches more than the first side. The third side is four inches less than three times the first. The perimeter is \(28\) inches. Find the length of the three sides of the triangle.
- Answer
-
The lengths of the sides of the triangle are \(5\), \(11\) and \(12\) inches.
EXAMPLE \(\PageIndex{27}\):
One side of a triangle is three feet less than the first side. The third side is five feet less than twice the first. The perimeter is \(20\) feet. Find the length of the three sides of the triangle.
- Answer
-
The lengths of the sides of the triangle are \(4\), \(7\) and \(9\) feet.
EXAMPLE \(\PageIndex{28}\):
The perimeter of a rectangular soccer field is \(360\) feet. The length is \(40\) feet more than the width. Find the length and width.
- Answer
-
Step 1. Read the problem. Step 2. Identify what we are looking for. the length and width of the soccer field Step 3. Name. Choose a variable to represent it. The length is 40 feet more than the width. Draw the figure and label it with the given information. Let w = width. \(w+40=\) length 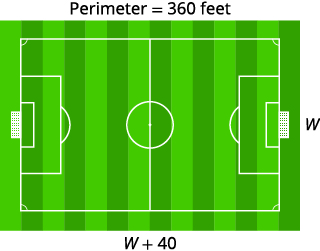
Step 4. Translate. Write the appropriate formula and substitute. 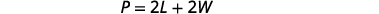
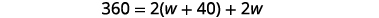
Step 5. Solve the equation. Step 6. Check. \( \begin{align*} P &=2L+2W \\ 360 & \stackrel{?}{=} 2(110)+2(70) \\360 &=360✓ \end{align*}\) 
Step 7. Answer the question. The length of the soccer field is \(110\) feet and the width is \(70\) feet.
EXAMPLE \(\PageIndex{29}\):
The perimeter of a rectangular swimming pool is \(200\) feet. The length is \(40\) feet more than the width. Find the length and width.
- Answer
-
The length of the swimming pool is \(70\) feet and the width is \(30\) feet.
EXAMPLE \(\PageIndex{30}\):
The length of a rectangular garden is \(30\) yards more than the width. The perimeter is \(300\) yards. Find the length and width.
- Answer
-
The length of the garden is \(90\) yards and the width is \(60\) yards.
Applications of these geometric properties can be found in many everyday situations as shown in the next example.
EXAMPLE \(\PageIndex{31}\):
Kelvin is building a gazebo and wants to brace each corner by placing a 10” piece of wood diagonally as shown.
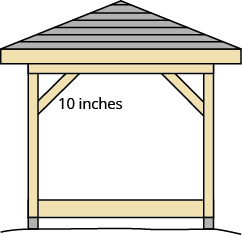
How far from the corner should he fasten the wood if wants the distances from the corner to be equal? Approximate to the nearest tenth of an inch.
- Answer
-
Step 1. Read the problem. Step 2. Identify what we are looking for. the distance from the corner that the bracket should be attached Step 3. Name. Choose a variable to represent it. Draw the figure and label it with the given information. Let \(x=\) the distance from the corner. 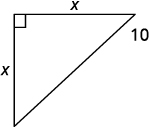
Step 4. Translate. Write the appropriate formula and substitute. \(a^2+b^2=c^2\) \(x^2+x^2=10^2\) Step 5. Solve the equation. Isolate the variable.
Use the definition of square root.Simplify. Approximate to the nearest tenth.
\( \begin{align*} 2x^2 &= 100 \\ \\ x^2 &=50 \\ \\ x &= \sqrt{50} \\ \\ x &≈7.1 \end{align*}\)
Step 6. Check. \( \begin{align*} a^2+b^2 &= c^2 \\ (7.1)^2+(7.1)^2 &≈10^2 \; \;\;\;\; \text{Yes.} \end{align*}\)
Step 7. Answer the question. Kelvin should fasten each piece of wood approximately 7.1” from the corner.
EXAMPLE \(\PageIndex{32}\):
John puts the base of a \(13\)-foot ladder five feet from the wall of his house as shown in the figure. How far up the wall does the ladder reach?

- Answer
-
The ladder reaches \(12\) feet.
EXAMPLE \(\PageIndex{33}\):
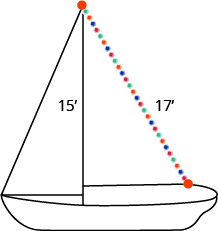
Randy wants to attach a \(17\)-foot string of lights to the top of the \(15\) foot mast of his sailboat, as shown in the figure. How far from the base of the mast should he attach the end of the light string?
- Answer
-
He should attach the lights \(8\) feet from the base of the mast.
Access this online resource for additional instruction and practice with solving for a variable in literal equations.
- Solving Literal Equations
Key Concepts
- How To Solve Geometry Applications
- Read the problem and make sure all the words and ideas are understood.
- Identify what you are looking for.
- Name what you are looking for by choosing a variable to represent it. Draw the figure and label it with the given information.
- Translate into an equation by writing the appropriate formula or model for the situation. Substitute in the given information.
- Solve the equation using good algebra techniques.
- Check the answer in the problem and make sure it makes sense.
- Answer the question with a complete sentence.
- The Pythagorean Theorem
- In any right triangle, where a and b are the lengths of the legs, and c is the length of the hypotenuse, the sum of the squares of the lengths of the two legs equals the square of the length of the hypotenuse.