2.7: Solve Linear Inequalities

In Chapter 1, we introduced the natural numbers \(\mathbb{N}=\big\{1,2,3, \ldots\big\}\), the whole numbers \(\mathbb{W}=\big\{0,1,2,3, \ldots\big\}\), and the integers \(\mathbb{Z}=\big\{\ldots,-3,-2,-1,0,1,2,3, \ldots\big\}\). Later in the chapter, we introduced the rational numbers, numbers of the form \(p/q\), where \(p\) and \(q\) are integers. We noted that both terminating and repeating decimals are rational numbers. Each of these numbers has a unique position on the number line (see Figure \(\PageIndex{1}\) ).

Figure \(\PageIndex{1}\): Positioning numbers on the number line.

The natural numbers, whole numbers, and integers are also rational numbers, because each can be expressed in the form \(\frac{p}{q}\), where \(p\) and \(q\) are integers. For example, \(0=\frac{0}{12}\), \(4 = \frac{4}{1}\), and \(-3=\frac{-12}{4}\). Indeed, the rational numbers contain all of the numbers we’ve studied up to this point in the course. However, not all numbers are rational numbers. For example, consider the decimal number \(-3.10110111011110 \ldots\), which neither terminates nor repeats. The number \(\sqrt{2}=1.414213562373095 \ldots\) also equals a decimal number that never terminates and never repeats. A similar statement can be made about the number \(\pi=3.141592653589793 \dots\) Each of these irrational (not rational) numbers also has a unique position on the number line (see Figure \(\PageIndex{2}\)).

Figure \(\PageIndex{2}\): Positioning numbers on the number line.

Two other irrational numbers you may encounter in your mathematical studies are \(e\) (Euler’s constant), which is approximately equal to \(e \approx 2.71828182845904 \ldots\), and \(\phi\) (pronounced “phi”), called the golden ratio, which equals \(\phi= \frac{1+\sqrt{5}}{2}\). The number \(e\) arises in applications involving compound interest, probability, and other areas of mathematics. The number \(\phi\) is used in financial markets and is also arguably the ratio of beauty in art and architecture.

The Real Numbers

If we combine all of the rational and irrational numbers into one collection, then we have a set of numbers that is called the set of real numbers. The set of real numbers is denoted by the symbol \(\mathbb{R}\).

Every point on the number line is associated with a unique real number. Conversely, every real number is associated with a unique position on the number line. In lieu of this correspondence, the number line is usually called the real line.

Ordering the Real Numbers

The real numbers are ordered on the real line in a manner identical to how we ordered the integers on the number line in Section 1 of Chapter 1.

Order on the Real Line

Suppose that \(a\) and \(b\) are real numbers positioned on the real line as shown below.

• Because \(a\) lies to the “left of” \(b\), we say that \(a\) is “less than” \(b\), or in mathematical symbols, \(a<b\). The inequality symbol \(<\) is read “less than.”
• Alternately, \(b\) lies to the “right of” \(a\), so we can also say that \(b\) is “greater than” \(a\), or in mathematical symbols, \(b>a\). The inequality symbol \(>\) is read “greater than.”

Here are two more inequality symbols that we will use in this section.

Less than or equal to

If we want to say that \(a\) lies to the “left of” \(b\), or shares the same position as \(b\), then we say that \(a\) is “less than or equal to” \(b\) and write \(a ≤ b\). The inequality symbol \(≤\) is pronounced “less than or equal to.”

Greater than or equal to

If we want to say that \(b\) lies to the “right of” \(a\), or shares the same position as \(a\), then we say that \(b\) is “greater than or equal to" \(a\) and write \(b≥ a\). The inequality symbol \(≥\) is pronounced “greater than or equal to.”

Set-Builder Notation

Mathematicians use a construct called set-builder notation to describe sets or collections of numbers. The general form of set-builder notation looks as follows: \[\big\{x \, | \,\text { some statement about } x\big\} \nonumber \]For example, suppose that we want to describe the set of “all real numbers that are less than \(2\).” We could use the following notation: \[A=\big\{x\, | \, x<2\big\} \nonumber \]

This is read aloud as follows: “\(A\) equals the set of all \(x\) such that \(x\) is less than \(2\).” Some prefer to use a colon instead of a vertical bar. \[A=\big\{x : x<2\big\} \nonumber \] In this text we use the vertical bar in set-builder notation, but feel free to use a colon instead. They mean the same thing. One might still object that the notation \[\big\{x\, | \, x<2\big\} \nonumber \] is a bit vague. One objection could be “What type of numbers \(x\) are you referring to? Do you want the integers that are less than two or do you want the real numbers that are less than two?” As you can see, this is a valid objection. One way of addressing this objection is to write: \[A=\big\{x \in \mathbb{R} \, | \, x<2\big\} \quad \text { or } \quad A=\big\{x \in \mathbb{N}\, | \, x<2\big\} \nonumber \] The first is read “\(A\) is the set of all \(x\) in \(R\) that are less than two,” while the second is read “\(A\) is the set of all \(x\) in \(N\) that are less than two.”

Set-builder Assumption

In this text, unless there is a specific reference to the set of numbers desired, we will assume that the notation \(\big\{x\, | \, x<2\big\}\) is asking for the set of all real numbers less than \(2\).

In Figure \(\PageIndex {3}\), we’ve shaded the set of real numbers \(\big\{x\, | \, x<2\big\}\). Because

Figure \(\PageIndex{3}\): Shading the numbers less than \(2\).

“less than” is the same as saying “left of,” we’ve shaded (in red) all points on the real line that lie to the left of the number two. Note that there is an “empty circle” at the number two. The point representing the number two is not shaded because we were only asked to shade the numbers that are strictly less than two.

While the shading in Figure \(\PageIndex{3}\) is perfectly valid, much of the information provided in Figure \(\PageIndex{3}\) is unnecessary (and perhaps distracting). We only need to label the endpoint and shade the real numbers to the left of two, as we’ve done in constructing Figure \(\PageIndex{4}\).

Figure \(\PageIndex{4}\): You only need to label the endpoint.

For contrast, suppose instead that we’re asked to shade the set of real numbers \(\big\{x\, | \, x\leq2\big\}\). This means that we must shade all the real numbers

Figure \(\PageIndex{5}\): You only need to label the endpoint.

that are “less than or equal to \(2\)” or “left of and including \(2\).” The resulting set is shaded in Figure \(\PageIndex{5}\).

Note the difference between Figures \(\PageIndex{4}\) and \(\PageIndex{45}\). In Figures \(\PageIndex{4}\) we’re shading the set \(\big\{x\, | \, x<2\big\}\), so the number \(2\) is left unshaded (an empty dot). In Figures \(\PageIndex{5}\), we’re shading the set \(\big\{x\, | \, x\leq2\big\}\), so the number \(2\) is shaded (a filled-in dot).

Example \(\PageIndex{1}\)

Shade the set \(\big\{x\, | \, x \geq-3\big\}\) on the real line.

Solution

The notation \(\big\{x\, | \, x \geq-3\big\}\) is pronounced “the set of all real numbers \(x\) such that \(x\) is greater than or equal to \(-3\).” Thus, we need to shade the number \(-3\) and all real numbers to the right of \(-3\).

Try It \(\PageIndex{1}\)

Shade \(\big\{x\, | \, x \leq 4\big\}\) on the real line.

Answer

 

Example \(\PageIndex{2}\)

Use set-builder notation to describe the set of real numbers that are shaded on the number line below.

Solution

The number \(-1\) is not shaded. Only the numbers to the left of \(-1\) are shaded. This is the set of all real numbers \(x\) such that \(x\) is “less than” \(-1\). Thus, we describe this set with the following set-builder notation: \[\big\{x\, | \, x<-1\big\} \nonumber \]

Try It \(\PageIndex{2}\)

Use set-builder notation to describe the following set of real numbers:

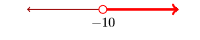
Answer

\(\big\{x\, | \, x>-10\big\}\)

Interval Notation

In Examples \(\PageIndex{1}\) and \(\PageIndex{2}\), we used set-builder notation to describe the set of real numbers greater than or equal to \(-3\) and a second set of real numbers less than \(-1\). There is another mathematical symbolism, called interval notation, that can be used to describe these sets of real numbers. Consider the first set of numbers from Example \(\PageIndex{1}\), \(\big\{x\, | \, x \geq-3\big\}\).

Sweeping our eyes “from left to right”, we use \([-3, \infty)\) to describe this set of real numbers. Some comments are in order:

1. The bracket at the left end means that \(-3\) is included in the set.
2. As you move toward the right end of the real line, the numbers grow without bound. Hence, the \(\infty\) symbol (positive infinity) is used to indicate that we are including all real numbers to the right of \(-3\). However, \(\infty\) is not really a number, so we use a parentheses to indicate we are “not including” this fictional point.

The set of numbers from Example \(\PageIndex {1}\) is \(\big\{x\, | \, x<-1\big\}\).

Sweeping our eyes “from left to right”, this set of real numbers is described with \((-\infty,-1)\). Again, comments are in order:

1. The number \(-1\) is not included in this set. To indicate that it is not included, we use a parenthesis.
2. As you move toward the left end of the real line, the numbers decrease without bound. Hence, the \(-\infty\) symbol (negative infinity) is used to indicate that we are including all real numbers to the left of \(-1\). Again, \(-\infty\) is not an actual number, so we use a parenthesis to indicate that we are not including this “fictional” point.

Sweep your eyes from “left to right”

If you would like to insure that you correctly use interval notation, place the numbers in your interval notation in the same order as they are encountered as you sweep your eyes from “left to right” on the real line.

A nice summary of set-builder and interval notation is presented in Table \(\PageIndex{1}\) at the end of the section.

Equivalent Inequalities

Like equations, two inequalities are equivalent if they have the same solution sets.

Adding or Subtracting the Same Quantity from Both Sides of an Inequality

Let \(a\) and \(b\) be real numbers with                     \(a < b  \)
If \(c\) is any real number, then             \(a + c<b+ c \) and \(a−c<b−c \).

That is, adding or subtracting the same amount from both sides of an inequality produces an equivalent inequality (does not change the solution).

Example \(\PageIndex{3}\)

Solve for \(x: \quad x-2 ≤ 7\). Sketch the solution on the real line, then use set-builder and interval notation to describe your solution.

Solution

To “undo” subtracting \(2\), we add \(2\) to both sides of the inequality.

\[\begin{aligned} x-2 &\leq 7 & & \color {Red} \text { Original inequality. } \\ x-2+2 &\leq 7+2 & & \color {Red} \text { Add } 2 \text { to both sides. } \\ x &\leq 9 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

To shade the real numbers less than or equal to \(9\), we shade the number \(9\) and all real numbers to the left of \(9\).

Using set-builder notation, the solution is \(\big\{x\, | \, x \leq 9\big\}\). Using interval notation, the solution is \((-\infty, 9]\).

Try It \(\PageIndex{3}\)

Use use set-builder and interval notation to describe the solution of: \(x−7 < −8\). 

Answer

Using set-builder notation, the solution is \(\big\{x\, |   x < -1   \big\}\). Using interval notation, the solution is  \((-\infty,-1)\)

If we multiply or divide both sides of an inequality by a positive number, we have an equivalent inequality.

Multiplying or Dividing by a Positive Number

Let \(a\) and \(b\) be real numbers with                         \(a<b\).
If \(c\) is a real positive number, then             \(a c<b c \) and \(\dfrac{a}{c}<\dfrac{b}{c} \)

Example \(\PageIndex{4}\)

Solve for \(x : \quad 3 x \leq-9\) Sketch the solution on the real line, then use set-builder and interval notation to describe your solution.

Solution

To “undo” multiplying by \(3\), divide both sides of the inequality by \(3\). Because we are dividing both sides by a positive number, we do not reverse the inequality sign.

\[\begin{aligned} 3x & \leq -9 & & \color {Red} \text { Original inequality. } \\ \dfrac{3x}{3} & \leq \dfrac{-9}{3} & & \color {Red} \text { Divide both sides by } 3. \\ x & \leq -3 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Shade the real numbers less than or equal to \(-3\).

Using set-builder notation, the solution is \(\big\{x\, | \, x \leq-3\big\}\). Using interval notation, the solution is \((-\infty,-3]\).

Try It \(\PageIndex{4}\)

Use use set-builder and interval notation to describe the solution of: \[2 x>-8 \nonumber \]

Answer

Using set-builder notation, the solution is \(\big\{x\, |   x > -4   \big\}\). Using interval notation, the solution is  \((-4, \infty)\)

Reversing the Inequality Sign

Up to this point, it seems that the technique for solving inequalities is pretty much identical to the technique used to solve equations. However, in this section we are going to encounter one exception.

Suppose we start with the valid inequality \(-2 < 5\), then we multiply both sides by \(2\), \(3\), and \(4\).

\[\begin{array}{rrrr}{-2<5} & {-2<5} & {-2<5} \\ {2(-2)<2(5)} & {3(-2)<3(5)} & {4(-2)<4(5)} \\ {-4<10} & {-6<15} & {-8<20}\end{array} \nonumber \]

Note that in each case, the resulting inequality is still valid.

\(\color{Red} \text {Caution! We’re about to make an error!} \)

Start again with \(−2 < 5\), but this time multiply both sides by \(−2\), \(−3\), and \(−4\).

\[\begin{array}{rrrr}{-2<5} & {-2<5} & {-2<5} \\ {-2(-2)<-2(5)} & {\;-3(-2)<-3(5)} & {\;-4(-2)<-4(5)} \\ {4<-10} & {6<-15} & {8<-20}\end{array} \nonumber \]

In each of the resulting inequalities, the inequality symbol is pointing the wrong way!

When you multiply both sides of an inequality by a negative number, you must reverse the inequality sign. Starting with \(−2 < 5\), multiply both sides by \(−2\), \(−3\), and \(−4\), but reverse the inequality symbol.

Some readers might prefer a more formal reason as to why we reverse the inequality when we multiply both sides by a negative number. Suppose that \(a<b\). Then, subtracting \(b\) from both sides gives the result \(a−b<0\). This means that \(a−b\) is a negative number. Now, if \(c\) is a negative number, then the product \((a−b)c\) is positive. Then:

\[\begin{aligned} a &<b \\ a - b &<0 \\ (a-b) c &>0 \\ a c-b c &>0 \\ a c-b c+b c &>0+b c \\ a c &>b c \end{aligned} \nonumber \]

Thus, if you start with \(a<b\) and \(c<0\), then \(ac > bc\).

Multiplying or Dividing by a Negative Number

Let \(a\) and \(b\) be real numbers with                     \(a<b\).
If \(c\) is a real negative number, then         \[a c>b c \) and \(\dfrac{a}{c}>\dfrac{b}{c} \)

That is, when multiplying or dividing both sides of an inequality by a negative number, you must reverse the inequality sign.

Example \(\PageIndex{5}\)

Solve for \(x: \quad −2x<4\). Sketch the solution on the real line, then use set-builder and interval notation to describe your solution.

Solution

To “undo” multiplying by \(−2\), divide both sides by \(−2\). Because we are dividing both sides by a negative number, we reverse the inequality sign.

\[\begin{aligned} -2 x&< 4 & & \color {Red} \text { Original inequality. } \\ \dfrac{-2x}{-2}&> \dfrac{4}{-2} & & \color {Red} \text { Divide both sides by }-2 \\ x&> -2 & & \color {Red} \text { Reverse the inequality sign. } \\ x&> -2 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Shade the real numbers greater than \(−2\).

Using set-builder notation, the solution is \(\big\{x\, | \, x>-2\big\}\). Using interval notation, the solution is \((-2, \infty)\).

Try It \(\PageIndex{5}\)

Use use set-builder and interval notation to describe the solution of: \[−3x≥− 6 \nonumber \]

Answer

Using set-builder notation, the solution is \(\big\{x\, |   x \leq 2   \big\}\). Using interval notation, the solution is \((-\infty, 2]\)

Multiple Steps

Sometimes you need to perform a sequence of steps to arrive at the solution. 

Example \(\PageIndex{6}\)

Solve for \(x: \quad 2 x +5> −7\). Sketch the solution on the real line, then use set-builder and interval notation to describe your solution.

Solution

To “undo” adding \(5\), subtract \(5\) from both sides of the inequality.

\[\begin{aligned} 2x+5&> -7 & & \color {Red} \text { Original inequality. } \\ 2x+5-5&> -7-5 & & \color {Red} \text { Subtract } 5 \text { from both sides. } \\ 2x&> -12 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

To “undo” multiplying by \(2\), divide both sides by \(2\). Because we are dividing both sides by a positive number, we do not reverse the inequality sign.

\[\begin{aligned} \dfrac{2x}{2}& >\dfrac{-12}{2} & & \color {Red} \text { Divide both sides by } 2 \\ x&> -6 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Shade the real numbers greater than \(−6\).

Using set-builder notation, the solution is \(\big\{x\, | \, x>-6\big\}\). Using interval notation, the solution is \((-6, \infty)\).

Try It \(\PageIndex{6}\)

Use use set-builder and interval notation to describe the solution of: \[3x-2 ≤4 \nonumber \]

Answer

Using set-builder notation, the solution is \(\big\{x\, |   x \leq 2   \big\}\). Using interval notation, the solution is \((-\infty, 2]\)

 

Example \(\PageIndex{7}\)

Solve for \(x: \quad 3 −5x ≤ 2x + 17\). Sketch the solution on the real line, then use set-builder and interval notation to describe your solution.

Solution

We need to isolate terms containing \(x\) on one side of the inequality. Start by subtracting \(2x\) from both sides of the inequality.

\[\begin{aligned} 3-5x &\leq 2x+17 & & \color {Red} \text { Original inequality. } \\ 3-5x-2x &\leq 2x+17-2x & & \color {Red} \text { Subtract } 2x \text { from both sides. } \\ 3-7x &\leq 17 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

We continue to isolate terms containing \(x\) on one side of the inequality. Subtract \(3\) from both sides.

\[\begin{aligned} 3-7x-3 &\leq 17-3 & & \color {Red} \text { Subtract } 3 \text { from both sides. } \\ -7x &\leq 14 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

To “undo” multiplying by \(−7\), divide both sides by \(−7\). Because we are dividing both sides by a negative number, we reverse the inequality sign.

\[\begin{aligned} \dfrac{-7x}{-7} &\geq \dfrac{14}{-7} & & \color {Red} \text { Divide both sides by }-7 \\ x &\geq-2 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Using set-builder notation, the solution is \(\big\{x\, | \, x \geq-2\big\}\). Using interval notation, the solution is \([-2, \infty)\).

Try It \(\PageIndex{7}\)

Use use set-builder and interval notation to describe the solution of: \[4-x>2x +1 \nonumber \]

Answer

Using set-builder notation, the solution is \(\big\{x\, |   x < 1   \big\}\). Using interval notation, the solution is \((-\infty, 1)\)

We clear fractions from an inequality in the usual manner, by multiplying both sides by the least common denominator.

Example \(\PageIndex{8}\)

Solve for \(x : \quad \quad \dfrac{3}{4}-\dfrac{x}{12}>\dfrac{1}{3}\).

Solution

First, clear the fractions from the inequality by multiplying both sides by the least common denominator, which in this case is \(12\).

\[\begin{aligned} \dfrac{3}{4}-\dfrac{x}{12} &>\dfrac{1}{3} & & \color {Red} \text { Original inequality. } \\ 12\left[\dfrac{3}{4}-\dfrac{x}{12}\right] &>\left[\dfrac{1}{3}\right] 12 & & \color {Red} \text { Multiply both sides by } 12.\\ 12\left[\dfrac{3}{4}\right]-12\left[\dfrac{x}{12}\right] &>\left[\dfrac{1}{3}\right] 12 & &  \color {Red} \text { Distribute the } 12.\\ 9-x &>4 & &  \color {Red} \text { Cancel and Multiply. } \end{aligned} \nonumber \]

To “undo” adding \(9\), subtract \(9\) from both sides.

\[\begin{aligned} 9-x-9 &> 4-9 & & \color {Red} \text { Subtract } 9 \text { from both sides. } \\ -x &> -5 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

We could divide both sides by \(−1\), but multiplying both sides by \(−1\) will also do the job. Because we are multiplying both sides by a negative number, we reverse the inequality sign.

\[\begin{aligned} (-1)(-x) &< (-5)(-1) & & \color {Red} \text { Multiply both sides by }-1. \text { Reverse the inequality sign. } \\ x &< 5 & & \color {Red} \text { Simplify both sides. } \end{aligned} \nonumber \]

Shade the real numbers less than \(5\).

Using set-builder notation, the solution is \(\big\{x\, | \, x<5\big\}\). Using interval notation, the solution is \((-\infty, 5)\).

Try It \(\PageIndex{8}\)

Use use set-builder and interval notation to describe the solution of: \[\dfrac{2 x}{3}-\dfrac{3}{4} \geq-\dfrac{3}{2} \nonumber \]

Answer

Using set-builder notation, the solution is \(\big\{x\, |   x \geq -\frac{9}{8}   \big\}\). Using interval notation, the solution is \([-\frac{9}{8}, \infty)\)

We clear decimals from an inequality in the usual manner, by multiplying both sides by the appropriate power of ten.

Example \(\PageIndex{9}\)

Solve for \(x : \quad 3.25-1.2 x>4.6\).

Solution

First, clear the decimals from the inequality by multiplying both sides by \(100\), which moves each decimal point two places to the right.

\[\begin{aligned} 3.25-1.2 x &>4.6 & & \color {Red} \text { Original inequality. }\\ 325-120 x &>460 & & \color {Red} \text { Multiply both sides by } 100.\\ 325-120 x-325 &>460-325 & & \color {Red} \text { Subtract } 325 \text { from both sides. }\\ -120 x &>135 & & \color {Red} \text { Simplify both sides. } \\ \dfrac{-120 x}{-120} &<\dfrac{135}{-120} & & \color {Red} \text { Divide both sides by } -120. \text { Reverse the inequality sign.}\\ x &<-\dfrac{9}{8} & & \color {Red} \text {Reduce to lowest terms.} \end{aligned} \nonumber \]

Shade the real numbers less than \(−9/8\).

Using set-builder notation, the solution is \(\big\{x\, | \, x<-9 / 8\big\}\). Using interval notation, the solution is \((-\infty,-9 / 8)\).

Try It \(\PageIndex{9}\)

Use use set-builder and interval notation to describe the solution of: \[2.3 x-5.62 \geq-1.4 \nonumber \]

Answer

Using set-builder notation, the solution is \(\big\{x\, | \, x \geq 1.83 \big\}\). Using interval notation, the solution is \(\big[\frac{211}{115}, \infty\big)\)

Solve Applications with Linear Inequalities

Many real-life situations require us to solve inequalities. The method we will use to solve applications with linear inequalities is very much like the one we used when we solved applications with equations.

We will read the problem and make sure all the words are understood. Next, we will identify what we are looking for and assign a variable to represent it. We will restate the problem in one sentence to make it easy to translate into an inequality. Then, we will solve the inequality.

Sometimes an application requires the solution to be a whole number, but the algebraic solution to the inequality is not a whole number. In that case, we must round the algebraic solution to a whole number. The context of the application will determine whether we round up or down.

Example \(\PageIndex{28}\)

Dawn won a mini-grant of $4,000 to buy tablet computers for her classroom. The tablets she would like to buy cost $254.12 each, including tax and delivery. What is the maximum number of tablets Dawn can buy?

Solution

Step 1. Read the problem.
Step 2. Identify what you are looking for.	the maximum number of tablets Dawn can buy
Step 3. Name what you are looking for. Choose a variable to represent that quantity.	Let \(n\) = the number of tablets.
Step 4. Translate Write a sentence that gives the information to find it.	$254.12  times the number of tablets is no more than $4,000.
\( \qquad \quad \) Translate into an inequality.	\( 254.12n\leq 4000  \)
Step 5. Solve the inequality.	\( n\leq 15.74 \) but \(n\) must be a whole number of tablets, so round to 15. \(  n\leq 15 \) tablets
Step 6. Check the answer in the problem and make sure it makes sense.	Rounding down the price to $250, 15 tablets would cost  $3,750,  while 16 tablets would be $4,000. So a maximum of 15 tablets at  $254.12 seems reasonable.
Step 7. Write a sentence that answers the question.	Dawn can buy a maximum of 15 tablets.

Try It \(\PageIndex{29}\)

Angie has $20 to spend on juice boxes for her son’s preschool picnic. Each pack of juice boxes costs $2.63. What is the maximum number of packs she can buy?

Answer

Angie can buy 7 packs of juice.

Try It \(\PageIndex{30}\)

Daniel wants to surprise his girlfriend with a birthday party at her favorite restaurant. It will cost $42.75 per person for dinner, including tip and tax. His budget for the party is $500. What is the maximum number of people Daniel can have at the party?

Answer

Daniel can have 11 people at the party.

Example \(\PageIndex{31}\)

Taleisha’s phone plan costs her $28.80 a month plus $0.20 per text message. How many text messages can she send/receive and keep her monthly phone bill no more than $50?

Solution

Step 1. Read the problem.
Step 2. Identify what you are looking for.	the number of text messages Taleisha can make
Step 3. Name what you are looking for. Choose a variable to represent that quantity.	Let \(t\) =  the number of text messages.
Step 4. Translate Write a sentence that gives the information to find it.	$28.80 plus  $0.20  times the number of text messages is less than or equal to $50.
\( \qquad \quad \) Translate into an inequality.	\(28.80+0.20t \leq 50 \)
Step 5. Solve the inequality.	\( 0.2t \leq 21.2 \) \(  t \leq 106 \) text messages
Step 6. Check the answer in the problem and make sure it makes sense.	Yes, \( 28.80+0.20(106)=50\).
Step 7. Write a sentence that answers the question.	Taleisha can send/receive no more than 106  text messages to keep her bill no more than $50.

Try It \(\PageIndex{32}\)

Sergio and Lizeth have a very tight vacation budget. They plan to rent a car from a company that charges $75 a week plus $0.25 a mile. How many miles can they travel during the week and still keep within their $200 budget?

Answer

Sergio and Lizeth can travel no more than 500 miles.

Try It \(\PageIndex{33}\)

Rameen’s heating bill is $5.42 per month plus $1.08 per therm. How many therms can Rameen use if he wants his heating bill to be a maximum of $87.50.

Answer

Rameen’s heating bill is $5.42 per month plus $1.08 per therm. How many therms can Rameen use if he wants his heating bill to be a maximum of $87.50.

Profit is the money that remains when the costs have been subtracted from the revenue. In the next example, we will find the number of jobs a small businesswoman needs to do every month in order to make a certain amount of profit.

Example \(\PageIndex{34}\)

Felicity has a calligraphy business. She charges $2.50 per wedding invitation. Her monthly expenses are $650. How many invitations must she write to earn a profit of at least $2,800 per month?

Solution

Step 1. Read the problem.
Step 2. Identify what you are looking for.	the number of invitations Felicity needs to write
Step 3. Name what you are looking for. Choose a variable to represent that quantity.	Let \(j\) =  the number of invitations.
Step 4. Translate Write a sentence that gives the information to find it.	$2.50 times the number of invitations minus $650 is at least $2,800.
\( \qquad \quad \) Translate into an inequality.	\( 2.50j−650\geq 2,800  \)
Step 5. Solve the inequality.	\( 2.5j\geq 3,450 \) \(  j\geq 1,380 \) invitations
Step 6. Check the answer in the problem and make sure it makes sense.	If Felicity wrote 1400 invitations, her profit would be \(2.50(1400)−650\), or $2,850. This is more than $2800.
Step 7. Write a sentence that answers the question.	Felicity must write at least 1,380 invitations.

Try It \(\PageIndex{35}\)

Caleb has a pet sitting business. He charges $32 per hour. His monthly expenses are $2,272. How many hours must he work in order to earn a profit of at least $800 per month?

Answer

Caleb must work at least 96 hours.

Try It \(\PageIndex{36}\)

Elliot has a landscape maintenance business. His monthly expenses are $1,100. If he charges $60 per job, how many jobs must he do to earn a profit of at least $4,000 a month?

Answer

Elliot must work at least 85 jobs.

There are many situations in which several quantities contribute to the total expense. We must make sure to account for all the individual expenses when we solve problems like this.

Example \(\PageIndex{37}\)

Malik is planning a six-day summer vacation trip. He has $840 in savings, and he earns $45 per hour for tutoring. The trip will cost him $525 for airfare, $780 for food and sightseeing, and $95 per night for the hotel. How many hours must he tutor to have enough money to pay for the trip?

Solution

Step 1. Read the problem.
Step 2. Identify what you are looking for.	the number of hours Malik must tutor
Step 3. Name what you are looking for. Choose a variable to represent that quantity.	Let \(h\) = the number of hours.
Step 4. Translate Write a sentence that gives the information to find it.	The expenses must be less than or equal to the income. The cost of airfare plus the cost of food and sightseeing and the hotel bill must be less than the savings plus the amount earned tutoring.
\( \qquad \quad \) Translate into an inequality.	\( 525+780+95(6)\leq 840+45h  \)
Step 5. Solve the inequality.	\( 1,875\leq 840+45h \) \( 1,035\leq 45h \) \(  h\geq 23 \) hours
Step 6. Check the answer in the problem and make sure it makes sense.	We substitute 23 into the inequality. \( 1,875\leq 840+45h \) \( 1,875\leq 840+45(23) \) \( 1,875\leq 1875 \)
Step 7. Write a sentence that answers the question.	Malik must tutor at least 23 hours.

Try It \(\PageIndex{38}\)

Brenda’s best friend is having a destination wedding and the event will last three days. Brenda has $500 in savings and can earn $15 an hour babysitting. She expects to pay $350 airfare, $375 for food and entertainment and $60 a night for her share of a hotel room. How many hours must she babysit to have enough money to pay for the trip?

Answer

Brenda must babysit at least 27 hours.

Try It \(\PageIndex{39}\)

Josue wants to go on a 10-night road trip with friends next spring. It will cost him $180 for gas, $450 for food, and $49 per night to share a motel room. He has $520 in savings and can earn $30 per driveway shoveling snow. How many driveways must he shovel to have enough money to pay for the trip?

Answer

Josue must shovel at least 20 driveways.

 

Summary Table of Set-Builder and Interval Notation

A summary table of the set-builder and interval notation is presented in Table \(\PageIndex{1}\).

Table \(\PageIndex{1}\): Examples of set-builder and interval notation.

Shading on the real line	Set-builder	Interval
	\(\big\{x\, | \, x>-5\big\}\)	\((-5, \infty)\)
	\(\big\{x \, | \, x \geq-5\big\}\)	\([-5, \infty)\)
	\(\big\{x\, | \, x<-5\big\}\)	\((-\infty,-5)\)
	\(\big\{x\, | \, x \leq-5\big\}\)	\((-\infty,-5]\)

Contributors and Attributions

• David Arnold (Retired Professor (Mathematics) at College of the Redwoods)