2.8: Solve Compound Inequalities
- Page ID
- 57585
In this section, we will explore compound inequalities. Like a compound sentence is the combination of two (or more) sentences into a larger sentence using conjunctions like "and" and "or", compound inequalities are statements formed by linking two (or more) inequalities together, either using the word "and" or "or", like
\(x \le -1\) or \(x > 5\),
or by creating a single statement (sometimes called a chain inequality) that incorporates multiple inequality symbols, e.g.,
\(-4 \le x < 7\).
In order to better understand how these compound inequalities work, we first need to define the intersection and union of two sets.
Intersection and Union
The intersection of two sets \(A\) and \(B\) is defined as follows.
The intersection of the sets \(A\) and \(B\) is the set of all objects that are in \(A\) and in \(B\).
In symbols, we write
\[A \cap B=\big\{x \, | \, x \in A \text { and } x \in B\big\}\]
In order to understand this definition, it’s absolutely crucial that we understand the meaning of the word “and.” The word “and” is a conjunction, used between statements \(P\) and \(Q\), as in “It is raining today and my best friend is the Lone Ranger.” In order to determine the truth or falsehood of this statement, you must first examine the truth or falsehood of the statements \(P\) and \(Q\) on each side of the word “and.”
The only way that the speaker is telling the truth is if both statements \(P\) and \(Q\) are true. In other words, the statement “It is raining today and my best friend is the Lone Ranger” is true if and only if the statement “It is raining today” is true and the statement “my best friend is the Lone Ranger” is also true. Logicians like to make up a construct called a truth table, like the one shown in Table \(\PageIndex{2}\).
Points in Table \(\PageIndex{2}\) to consider:
| \(P\) | \(Q\) | \(P\) and \(Q\) |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
- In the first row (after the header row) of Table \(\PageIndex{2}\), if statements \(P\) and \(Q\) are both true (indicated with a T), then the statement “\(P\) and \(Q\)” is also true.
- In the remaining rows of Table \(\PageIndex{2}\), one or the other of statements \(P\) or \(Q\) are false (indicated with an F), so the statement “\(P\) and \(Q\)” is also false.
Therefore, the statement “\(P\) and \(Q\)” is true if and only if \(P\) is true and \(Q\) is true.
If \(A = \big\{1, 3, 5, 7, 9\big\}\) and \(B = \big\{2, 5, 7, 8, 11\big\},\) find the intersection of \(A\) and \(B.\)
Solution
As a reminder, the intersection of sets \(A\) and \(B\) is
\[A \cap B=\big\{x \, | \, x \in A \text { and } x \in B\big\}\]
Thus, we are looking for the objects that are in \(A\) and in \(B.\) The only objects that are in \(A\) and in \(B\) (remember, both statements “in \(A\)” and “in \(B\)” must be true) are 5 and 7, so we write:
\[A \cap B=\big\{5,7\big\}\]
Mathematicians and logicians both use a visual aid called a Venn Diagram to represent sets. John Venn was an English mathematician who devised this visualization of logical relationships. Consider the ellipse \(A\) in Figure \(\PageIndex{5}\). Everything inside the boundary of this ellipse constitutes the set \(A = \big\{1, 3, 5, 7, 9\big\}.\) That’s why you see these numbers inside the boundary of this ellipse.
Consider the ellipse \(B\) in Figure \(\PageIndex{5}\). Everything inside the boundary of this ellipse constitutes the set \(B = \big\{2, 5, 7, 8, 11\big\}.\) That’s why you see these numbers inside the boundary of this ellipse.
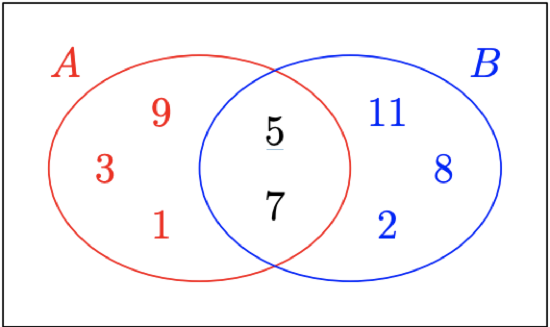
Now, note that only two numbers, \(5\) and \(7,\) are contained within the boundaries of both \(A\) and \(B.\) These are the numbers that are in the intersection of the sets \(A\) and \(B.\)
The shaded region in Figure \(\PageIndex{6}\) is the area that belongs to both of the sets \(A\) and \(B.\) Note how this shaded region is aptly named “the intersection of the sets \(A\) and \(B.\)” This is the region that is in common to the sets \(A\) and \(B,\) the region where the sets \(A\) and \(B\) overlap or “intersect.”
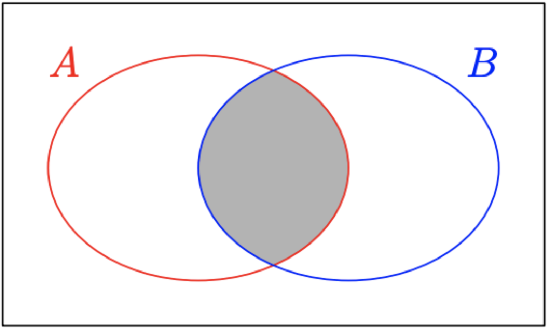
This leads to the following important piece of advice.
When asked to find the intersection of two sets \(A\) and \(B,\) look to see where the sets intersect or overlap. That is, look to see the elements that are in both sets \(A\) and \(B.\)
Let’s move on to the definition of the union of two sets \(A\) and \(B.\)
The union of the sets \(A\) and \(B\) is the set of all objects that are in \(A\) or in \(B.\)
In symbols, we write
\[A \cup B=\big\{x \, | \, x \in A \text { or } x \in B\big\}\]
In order to understand this definition, it’s critical that we understand the meaning of the word “or.” The word “or” is a disjunction, used between statements \(P\) and \(Q,\) as in “It is raining today or my best friend is the Lone Ranger.” In order to determine the truth or falsehood of this statement, you must first examine the truth or falsehood of the statements \(P\) and \(Q\) on each side of the word “or.”
The speaker is telling the truth if either statement \(P\) is true or statement \(Q\) is true. In other words, the statement “It is raining today or my best friend is the Lone Ranger” is true if and only if the statement “It is raining today” is true or the statement “my best friend is the Lone Ranger” is true. Logicians like to make up a construct called a truth table, like the one shown in Table \(\PageIndex{3}\).
| \(P\) | \(Q\) | \(P\) or \(Q\) |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
Points in Table \(\PageIndex{3}\) to consider:
- In the last row of Table \(\PageIndex{3}\), both statements \(P\) and \(Q\) are false (indicated with an F), so the statement \(P\) or \(Q\) is also false.
- In the first three rows (after the header row) of Table \(\PageIndex{3}\), either statement \(P\) is true or statement \(Q\) is true (indicated with a T), so the statement \(P\) or \(Q\) is also true.
Therefore, the statement “\(P\) or \(Q\)” is true if and only if either statement, \(P\) or \(Q,\) is true.
If \(A = \big\{1, 3, 5, 7, 9\big\}\) and \(B = \big\{2, 5, 7, 8, 11\big\},\) find the union of \(A\) and \(B.\)
Solution
As a reminder, the union of \(A\) and \(B\) is \[A \cup B=\big\{x \, | \, x \in A \text { or } x \in B\big\}\]
Thus, an object is in the union of \(A\) and \(B\) if and only if it is in either set. The numbers that are in either set are the numbers \[A \cup B=\big\{1,2,3,5,7,8,9,11\big\}\]
If we look again at the Venn Diagram in Figure \(\PageIndex{5}\), we see that this union \(A \cup B = \big\{1, 2, 3, 5, 7, 8, 9, 11\big\}\) lists every number that is in either set in Figure \(\PageIndex{5}\).
Thus, the shaded region in Figure \(\PageIndex{7}\) is the union of sets \(A\) and \(B.\) Note how this region is well-named, as that’s what you’re actually doing, taking the “union” of the two sets \(A\) and \(B.\) That is, the union contains all elements that belong to either \(A\) or \(B.\) Less formally, the union is a way of combining everything that occurs in either set.
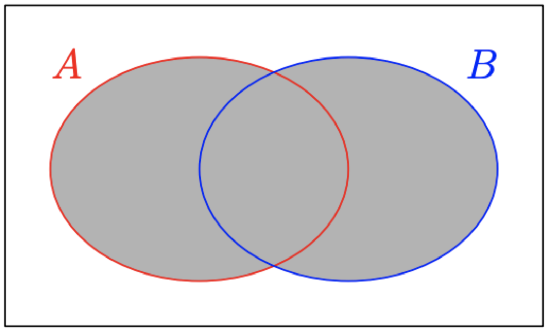
This leads to the following important piece of advice.
When asked to find the union of two sets \(A\) and \(B,\) in your answer, include everything from both sets.
Simple Compound Inequalities
Let’s apply what we’ve learned to find the unions and/or intersections of intervals of real numbers. The easiest approach is through a series of examples. Let’s begin.
On the real line, sketch the set of real numbers in the set \(\big\{x \, | \, x < 3\) or \(x < 5\big\}.\) Use set-builder notation and interval notation to describe your final answer.
Solution
First, let’s sketch two sets, \(\big\{x \, | \, x < 3\big\}\) and \(\big\{x \, | \, x < 5\big\},\) on separate real lines, one above the other as shown in Figure \(\PageIndex{8}\).
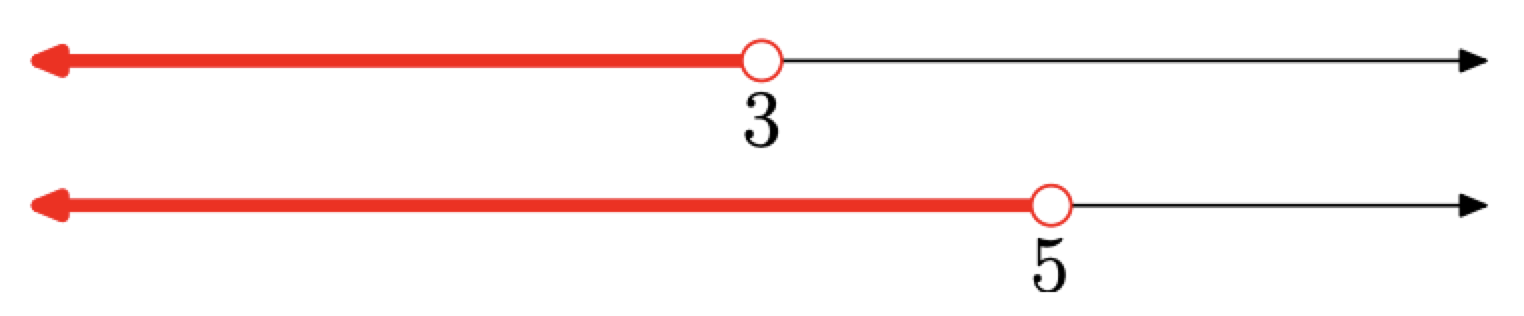
Now, to sketch the solution, note the word “or” in the set \(\big\{x \, | \, x < 3\) or \(x < 5\big\}.\) Thus, we need to take the union of the two shaded real lines in Figure \(\PageIndex{8}\). That is, we need to shade everything that is shaded on either of the two number lines. Of course, this would be everything less than 5, as shown in Figure \(\PageIndex{9}\).

Thus, the final simplified solution is
Set-Builder Notation: \(\big\{x \, | \, x < 5\big\}\)
Interval notation: \((-\infty, 5)\)
Let’s look at another example.
On the real line, sketch the set of real numbers in the set \(\big\{x \, | \, x < 3\) and \(x < 5\big\}.\) Use interval notation to describe your final answer.
Solution
In Example \(\PageIndex{3}\), you were asked to shade the set \(\big\{x \, | \, x < 3\) or \(x < 5\big\}\) on the real line. In this example, we’re asked to sketch the set \(\big\{x \, | \, x < 3\) and \(x < 5\big\}.\) Note that the set-builder notations are identical except for one change, the “or” of Example \(\PageIndex{3}\) has been replaced with the word “and.”
Our solution will be the numbers that are solutions to both inequalities known as the intersection of the two inequalities. Consider the intersection of two streets—the part where the streets overlap—belongs to both streets.
To find the solution of an "and" compound inequality, we look at the graphs of each inequality and then find the numbers that belong to both graphs—where the graphs overlap.
Again, sketch two sets, \(\big\{x \, | \, x < 3\big\}\) and \(\big\{x \, | \, x < 5\big\},\) on separate real lines, one above the other as shown in Figure \(\PageIndex{11}\).
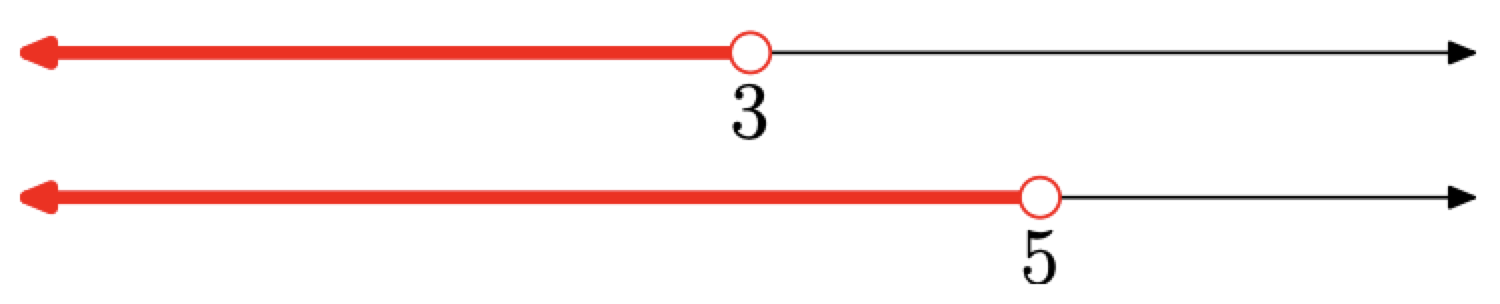
Now, to sketch the solution, note the word “and” in the set \(\big\{x \, | \, x < 3\) and \(x < 5\big\}.\) Thus, we need to take the intersection of the two shaded real lines in Figure \(\PageIndex{11}\). That is, we need to shade everything that is common to the two number lines. Here this would be everything less than 3, as shown in Figure \(\PageIndex{12}\).

Thus, the final simplified solution is
Set-Builder Notation: \(\big\{x \, | \, x < 3\big\}\)
Interval notation: \((-\infty, 3)\).
If you answer “or” when the answer requires “and,” or vice-versa, you have not made a minor mistake. Indeed, this is a huge error, as demonstrated in Example \(\PageIndex{3}\) and Example \(\PageIndex{4}\).
Before attempting another example, we pause to define a bit of notation that will be extremely important in our upcoming work.
The notation
\[a<x<b\]
is interpreted to mean
\[x>a \text { and } x<b\]
Alternatively, we could have said that \(a < x < b\) is identical to saying “\(a < x\) and \(x < b,\)” but saying “\(a < x\)” is the same as saying “\(x > a.\)” We prefer to say “\(x > a\) and \(x < b,\)” and will use this order throughout our work, but the form “\(a < x\) and \(x < b\)” is equally valid.
The really key point to make here is the fact that the statement \(a < x < b\) is an “and” statement. If it is used properly, it’s a good way to describe the numbers that lie between \(a\) and \(b.\)
Let’s look at an example.
On the real line, sketch the set of real numbers in the set \(\big\{x \, | \, x>3 \text { and } x<5\big\}.\) Give both the simplified set-builder notation and interval notation to describe your answer.
Solution
The first step is to sketch the sets \(\big\{x \, | \, x > 3\big\}\) and \(\big\{x \, | \, x < 5\big\}\) on individual real lines, stacked one above the other, as shown in Figure \(\PageIndex{13}\).

Now, to sketch the solution, note the word “and” in the set \(\big\{x \, | \, x > 3\) and \(x < 5\big\}.\) Thus, we need to take the intersection of the two graphs in Figure \(\PageIndex{13}\). That is, we need to shade the numbers on the real line that are in common to the two graphs shown in Figure \(\PageIndex{13}\). The numbers 3 and 5 are not shaded in both sets in Figure \(\PageIndex{13}\), so they will not be shaded in our final solution. However, all real numbers between 3 and 5 are shaded in both sets in Figure \(\PageIndex{13}\), so these numbers will be shaded in the final solution shown in Figure \(\PageIndex{14}\).

Since the numbers that make the original compound inequality true are just those that are between \(3\) and \(5\) on the number line, we can simplify the condition in set-builder notation to
Set-Builder Notation: \(\big\{x \, | \, 3<x<5\big\}\)
And the interval notation for the shaded solution in Figure \(\PageIndex{14}\) is
Interval Notation: \((3, 5)\)
Similarly, here are the set-builder and interval notations, as well as shading of the sets on the real line, for several situations, including the one just discussed.
| Number line graph | Set-builder notation | Interval notation |
|---|---|---|
 |
\(\big\{x \, | \, 3 < x < 5\big\}\) | \((3,5)\) |
 |
\(\big\{x \, | \, 3 \leq x \leq 5\big\}\) |
\([3,5]\) |
 |
\(\big\{x \, | \, 3 \leq x < 5\big\}\) | \([3,5)\) |
 |
\(\big\{x \, | \, 3 < x \leq 5\big\}\) | \((3,5]\) |
There are several points of emphasis regarding the intervals in Table \(\PageIndex{4}\).
- When we want to emphasize that we are not including a point on the real line, we use an “empty circle.” Conversely, a “filled circle” means that we are including the point on the real line. Thus, the interval in the first row of Table \(\PageIndex{4}\) does not include the endpoints at 3 and 5, but the interval in the second row of Table \(\PageIndex{4}\) does include the endpoints at 3 and 5.
- The use of a parenthesis in interval notation means that we are not including that endpoint in the interval. Thus, the parentheses used in \((3, 5)\) in the first row of Table \(\PageIndex{4}\) means that we are not including the numbers 3 and 5 in that interval.
- The use of a bracket in interval notation means that we are including the bracketed number in the interval. Thus, the brackets used in \([3, 5],\) as seen in the second row of Table \(\PageIndex{4}\), means that we are including the numbers 3 and 5 in the interval.
- Finally, note that some of our intervals are “open” on one end but “closed” (filled) on the other end, such as those in rows 3 and 4 of Table \(\PageIndex{4}\).
Some terminology:
- The interval \((3, 5)\) is open at each end. Therefore, we call the interval \((3, 5)\) an open interval.
- The interval \([3, 5]\) is closed (filled) at each end. Therefore, we call the interval \([3, 5]\) a closed interval.
- The intervals \((3, 5]\) and \([3, 5)\) are neither open nor closed.
Let’s look at another example.
On the real line, sketch the set of all real numbers in the set \(\big\{x \, | \, x > 3\) or \(x < 5\big\}\). Use set-builder notation and interval notation to describe your answer.
Solution
Note that the only difference between this current example and the set shaded in Example \(\PageIndex{4}\) is the fact that we’ve replaced the word “and” in \(\big\{x \, | \, x > 3\) and \(x < 5\big\}\) with the word “or” in \(\big\{x \, | \, x > 3\) or \(x < 5\big\}\). But, as we’ve seen before, this can make a world of difference.
Thus, the first step is to sketch the sets \(\big\{x \, | \, x > 3\big\}\) and \(\big\{x \, | \, x < 5\big\}\) on individual real lines, stacked one above the other, as shown in Figure \(\PageIndex{15}\).

Now, to sketch the solution, note the word “or” in the set \(\big\{x \, | \, x > 3\) or \(x < 5\big\}\). Thus, we need to take the union of the two graphs in Figure \(\PageIndex{15}\). That is, we need to shade the numbers on the real line that are shaded on either of the two graphs shown in Figure \(\PageIndex{15}\). However, this means that we will have to shade every number on the line, as shown in Figure \(\PageIndex{16}\). You’ll note no labels for \(3\) and \(5\) on the real line in Figure \(\PageIndex{16}\), as there are no endpoints in this solution. The endpoints, if you will, are at negative and positive infinity.

Thus, in a most natural way, the interval notation for the shaded solution in Figure \(\PageIndex{16}\) is
Interval Notation: \((-\infty, \infty).\)
The set-builder notation for this solution needs to represent the whole real line or all real numbers, so we write it in the following way:
Set-Builder Notation: \(\big\{x \, | \, x \in \mathbb{R}\big\}\).
Let’s look at another example.
On the real line, sketch the set of all real numbers in the set \(\big\{x \, | \, x < −1\) or \(x > 3\big\}\). Use interval notation to describe your answer.
Solution
The first step is to sketch the sets \(\big\{x \, | \, x < −1\big\}\) and \(\big\{x \, | \, x > 3\big\}\) on separate real lines, stacked one above the other, as shown in Figure \(\PageIndex{17}\).

To sketch the solution, note the word “or” in the set \(\big\{x \, | \, x < −1\) or \(x > 3\big\}\). Thus, we need to take the union of the two shaded real lines in Figure \(\PageIndex{17}\). That is, we need to shade the numbers on the real line that are shaded on either real line in Figure \(\PageIndex{17}\). Thus, every number smaller than \(−1\) is shaded, as well as every number greater than 3. The result is shown in Figure \(\PageIndex{18}\).

Since the graph of this solution is not a single interval on the numberline, but is instead made up of two disjoint (non-overlapping) intervals, in this one situation, we will need to leave the word "or" in the condition in the set-builder notation for this solution.
Set-Builder Notation: \(\big\{x \, | \, x < −1\) or \(x > 3\big\}\)
Next let's figure out how to write this solution using interval notation.
Here is an important tip.
If you wish to use interval notation correctly, follow one simple rule: Always sweep your eyes from left to right describing what you see shaded on the real line.
If we follow this advice, as we sweep our eyes from left to right across the real line shaded in Figure \(\PageIndex{18}\), we see that numbers are shaded from negative infinity to \(−1,\) and from \(3\) to positive infinity. Thus, in a most natural way, the interval notation for the shaded solution set in Figure \(\PageIndex{18}\) is
Interval Notation: \((-\infty,-1) \cup(3, \infty)\)
There are several important points to make here:
Note how we used the union symbol \(\cup\) to join the two intervals in \((-\infty,-1) \cup(3, \infty)\) in a natural manner.
The union symbol is used between sets of numbers, while the word “or” is used between statements about numbers. Thus it is incorrect to exchange the roles of the union symbol and the word “or.” Thus, writing \(\big\{x \, | \, x<-1 \cup x>3\big\}\) is incorrect, as it would also be to write \((-\infty,-1)\) or \((3, \infty)\).
Note that we will never use an intersection symbol ( \( \cap \) ) in our interval notation. Intersections of intervals can always be simplified to a single interval. Only unions (combined using the word "or") can form solutions made up of disjoint (non-connected) intervals like the one shown in Figure \(\PageIndex{18}\).
Let's reinforce our earlier discussion about the difference between “filled” and “open” circles, brackets, and parentheses using the examples shown below in Table \(\PageIndex{5}\). Here we include several comparisons of interval and set-builder notation, including the current solution to Example \(\PageIndex{7}\).
| Number line graph | Set-builder notation | Interval notation |
|---|---|---|
 |
\(\big\{x \, | \, x<-1\) or \(x>3\big\}\) | \((-\infty,-1) \cup(3, \infty)\) |
 |
\(\big\{x \, | \, x \leq-1\) or \(x \geq 3\big\}\) | \((-\infty,-1] \cup[3, \infty)\) |
 |
\(\big\{x \, | \, x \leq-1\) or \(x>3\big\}\) | \((-\infty,-1] \cup(3, \infty)\) |
 |
\(\big\{x \, | \, x<-1\) or \(x \geq 3\big\}\) | \((-\infty,-1) \cup[3, \infty)\) |
Again, we reinforce the following points.
- Note how sweeping your eyes from left to right, describing what is shaded on the real line, insures that you write the interval notation in the correct order.
- A bracket is equivalent to a filled dot and includes the endpoint, while a parenthesis is equivalent to an open dot and does not include the endpoint.
Let’s do one last example that should forever cement the notion that there is a huge difference between the words “and” and “or.”
On the real line, sketch the set of all real numbers in the set \(\big\{x \, | \, x<-1\) and \(x>3\big\}\). Describe your solution.
Solution
First and foremost, note that the only difference between this example and Example \(\PageIndex{6}\) is the fact that we changed the “or” in \(\big\{x \, | \, x<-1\) or \(x>3\big\}\) to an “and” in \(\big\{x \, | \, x<-1\) and \(x>3\big\}\). The preliminary sketches are identical to those in Figure \(\PageIndex{17}\).

Now, note the word “and” in \(\big\{x \, | \, x < −1\text{ and }x > 3\big\}\). Thus, we need to take the intersection of the shaded real lines in Figure \(\PageIndex{19}\). That is, we need to shade on a single real line all of the numbers that are shaded on both real lines in Figure \(\PageIndex{19}\). However, there are no points shaded in common on the real lines in Figure \(\PageIndex{19}\), so the solution set is empty, as shown in Figure \(\PageIndex{20}\).

This compound inequality has No Solution, so we would write its solution set as: \(\big\{ \big\}\).
There would be no way to write interval notation or set-builder notation in this case.
Pretty impressive! The last two examples clearly demonstrate that if you interchange the roles of “and” and “or,” you have not made a minor mistake. Indeed, you’ve changed the whole meaning of the problem. So, be careful with your “ands” and “ors.”
Solving Compound Inequalities
We now turn our attention to the business of solving compound inequalities.
In this case, the best way of learning is by doing. Let’s start with an example.
Solve the following compound inequality for \(x.\)
\[3-2 x<-1 \quad \text { or } \quad 3-2 x>1 \nonumber\]
Solution
First, solve each of the inequalities independently. With the first inequality, add \(−3\) to both sides of the inequality, then divide by \(−2,\) reversing the inequality sign.
\[\begin{align*} 3-2 x &<-1 \\-2 x &<-4 \\ x &>2 \end{align*}\]
Shade the solution on a number line.

The exact same sequence of operations can be used to solve the second inequality
\[\begin{align*} 3-2 x &>1 \\-2 x &>-2 \\ x &<1 \end{align*}\]

Although you solve each side of the inequality independently, you will want to arrange your work as follows, stacking the number line solution for the first inequality above that of the second inequality.
\[\begin{array}{rlllrll}{3-2 x}&{<}&{-1} & {\text { or }} & {\quad 3-2 x}&{>}&{1} \\ {-2 x}&{<}&{-4} & &{-2 x}&{>}&{-2} \\ {x}&{>}&{2} && {x}&{<}&{1}\end{array} \nonumber\]


The answer, described in both interval and set-builder notation, is
Interval Notation: \((-\infty, 1) \cup(2, \infty)\)
Set-Builder Notation: \(\big\{x\, | \,<1 \text { or } x>2\big\}.\)
Let’s look at another example.
Solve the following compound inequality for \(x.\)
\[3-2 x>-1 \quad \text { and } \quad 3-2 x<1 \label{eq13}\]
Solution
Solve each inequality independently, arranging your work as follows.
\[\begin{array}{rlllrll}{3-2 x}&{>}&{-1} & {\text { and }} & {\quad 3-2 x}&{<}&{1} \\ {-2 x}&{>}&{-4} & &{-2 x}&{<}&{-2} \\ {x}&{<}&{2} && {x}&{>}&{1}\end{array} \label{eq14}\]
Shade the solution of each inequality on separate real lines, one above the other


The answer, described in both interval and set-builder notation, is
Interval Notation: \((1,2)\)
Set-Builder Notation: \(\big\{x \, | \, 1<x<2\big\}\)
Note that we used the compact form of the compound inequality in our answer, as this condition is simpler than using an "and" compound inequality.
Alternative approach. You might have noted that in solving the second inequality in \ref{eq14}, you found yourself repeating the identical operations used to solve the first inequality. That is, you subtracted \(3\) from both sides of the inequality, then divided both sides of the inequality by \(−2,\) reversing the inequality sign.
This repetition is annoying and suggests a possible shortcut in this particular situation. Because the statement \(x > a\) and \(x < b\) is identical to the statement \(a < x < b\), solving the two part "AND" inequality (as in \ref{eq13}) could be solved more efficiently by first rewriting it in its equivalent "chain" inequality form
\[-1<3-2 x<1 \label{eq16}\]
Now, here are the rules for working with this form.
When working with a compound inequality having the form
\[a<x<b\]
you may add (or subtract) the same amount to (from) all three parts of the inequality, as in
\[a+c<x+c<b+c\]
or
\[a-c<x-c<b-c\]
You may also multiply all three parts by the same positive number \(c > 0,\) as in
\[c a<c x<c b\]
However, if you multiply all three parts by the same negative number \(c < 0,\) then don’t forget to reverse the inequality signs, as in
\[c a>c x>c b\]
The rules for division are identical to the multiplication rules. If \(c > 0\) (positive), then
\[\frac{a}{c}<\frac{x}{c}<\frac{b}{c}\]
If \(c < 0\) (negative), then reverse the inequality signs when you divide.
\[\frac{a}{c}>\frac{x}{c}>\frac{b}{c}\]
Each of the tools in Property \(\PageIndex{4}\) always produce equivalent inequalities.
So, let’s return to the compound inequality \ref{eq13}. The following example solves it using its equivalent "Chain" inequality form \ref{eq16}.
Solve the following compound inequality for \(x.\)
\[-1<3-2 x<1 \label{eq12}\]
Solution
\[\begin{array}{c}{-1<3-2 x<1} \\ {-1-3<3-2 x-3<1-3} \\ {-4<-2 x<-2}\end{array} \nonumber\]
Next, divide all three members by \(−2,\) reversing the inequality signs as you do so.
\[\begin{array}{c}{-4<-2 x<-2} \\ {\dfrac{-4}{-2}>\dfrac{-2 x}{-2}>\dfrac{-2}{-2}} \\ {2>x>1}\end{array} \nonumber\]
It is conventional to change the order of this last inequality. By reading the inequality from right to left, we get
\[1<x<2 \nonumber\]
which describes the real numbers that are greater than 1 and less than \(2.\) The solution is drawn on the following real line.

Note that this is identical to the solution set on the real line in Figure \(\PageIndex{22}\). Note also that this second alternative method is more efficient, particularly if you do a bit of work in your head. Consider the following sequence where we subtract three from all three members, then divide all three members by \(−2,\) reversing the inequality signs, then finally read the inequality in the opposite direction.
\[\begin{array}{c}{-1<3-2 x<1} \\ {-4<-2 x<-2} \\ {\quad 2>x>1} \\ {\quad 1<x<2}\end{array} \nonumber\]
Let’s look at another example.
Solve the following compound inequality for \(x.\)
\[-1<x-\frac{x+1}{2} \leq 2 \nonumber\]
Solution
First, let’s multiply all three members by \(2,\) in order to clear the fractions.
\[2(-1)<2\left(x-\frac{x+1}{2}\right) \leq 2(2) \nonumber\]
\[-2<2(x)-2\left(\frac{x+1}{2}\right) \leq 4 \nonumber\]
Cancel. Note the use of parentheses, which is crucial when a minus sign is involved.
\[-2<2 x-\cancel{2}\left(\frac{x+1}{\cancel{2}}\right) \leq 4 \nonumber\]
\[-2<2 x-(x+1) \leq 4 \nonumber\]
Distribute the minus sign and simplify.
\[\begin{align*} -2 &< &&2x-x-1 &&\leq 4 \\ -2 &< &&x-1&& \leq 4 \end{align*}\]
Add \(1\) to all three members and simplify.
\[ -2+1 < x-1+1 \leq 4+1 \nonumber\]
\[-1<x \leq 5 \nonumber\]
This solution describes the real numbers that are greater than \(-1\) and less than \(5,\) including \(5.\) That is, the real numbers that fall between \(-1\) and \(5,\) including \(5,\) shaded on the real line in Figure \(\PageIndex{24}\).

The answer, described in both interval and set-builder notation, is
Interval Notation: \((-1,5]\)
Set-Builder Notation: \(\big\{x\, | \,-1<x \leq 5\big\}\)
Let’s look at another example.
Solve the following compound inequality for \(x.\)
\[x \leq 2 x-3 \leq 5 \nonumber\]
Solution
Suppose that we try to isolate \(x\) as we did in Example \(\PageIndex{11}\). Perhaps we would try adding \(−x\) to all three members.
\[\begin{align*} x &\leq &&2x-3 &&\leq 5 \\ x-x &\leq &&2x-3-x &&\leq 5-x \\ 0 &\leq &&x-3 &&\leq 5-x \end{align*}\]
Well, that didn’t help much, just transferring the problem with \(x\) to the other end of the inequality. Similar attempts will not help in isolating \(x.\) So, what do we do?
The solution is we split the inequality (with the word “and,” of course).
\[x \leq 2 x-3 \quad \text { and } \quad 2 x-3 \leq 5 \nonumber\]
We can solve the first inequality by subtracting \(2x\) from both sides of the inequality, then multiplying both sides by \(−1,\) reversing the inequality in the process
\[\begin{align*} x & \leq 2 x-3 \\-x & \leq-3 \\ x & \geq 3 \end{align*}\]
To solve the second inequality, add \(3\) to both sides, then divide both sides by \(2\):
\[\begin{align*} 2 x-3 & \leq 5 \\ 2 x & \leq 8 \\ x & \leq 4 \end{align*}\]
Of course, you’ll probably want to arrange your work as follows
\[\begin{array}{rllrl} x & \leq 2 x-3 & \text{and} &2 x-3 & \leq 5 \\ -x & \leq-3 && 2 x & \leq 8 \\ x & \geq 3 & & x & \leq 4\end{array} \nonumber\]
Thus, we need to shade on a number line all real numbers that are greater than or equal to \(3\) and less than or equal to \(4,\) as shown in Figure \(\PageIndex{25}\).

The solution, described in both interval and set-builder notation, is
Interval Notation: \([3,4]\)
Set-Builder Notation: \(\big\{x\, | \, 3 \leq x \leq 4\big\}\)
Contributors
Adapted and customized by Paul Seeburger (Monroe Community College) based primarily on material by
David Arnold (Retired Professor (Mathematics) at College of the Redwoods)
Figure \(\PageIndex{10}\) and some of the surrounding text comes from Section 2.7 of the OpenStax Intermediate Algebra text by Lynn Marecek.

