5.6E: Exercises
- Last updated
- Save as PDF
- Page ID
- 30530
Practice Makes Perfect
Determine Whether an Ordered Pair is a Solution of a System of Linear Inequalities
In the following exercises, determine whether each ordered pair is a solution to the system.
Exercise \(\PageIndex{1}\)
\(\left\{\begin{array}{l}{3 x+y>5} \\ {2 x-y \leq 10}\end{array}\right.\)
- (3,−3)
- (7,1)
- Answer
-
- true
- false
Exercise \(\PageIndex{2}\)
\(\left\{\begin{array}{l}{4 x-y<10} \\ {-2 x+2 y>-8}\end{array}\right.\)
- (5,−2)
- (−1,3)
Exercise \(\PageIndex{3}\)
\(\left\{\begin{array}{l}{y>\frac{2}{3} x-5} \\ {x+\frac{1}{2} y \leq 4}\end{array}\right.\)
- (6,−4)
- (3,0)
- Answer
-
- false
- true
Exercise \(\PageIndex{4}\)
\(\left\{\begin{array}{l}{y<\frac{3}{2} x+3} \\ {\frac{3}{4} x-2 y<5}\end{array}\right.\)
- (−4,−1)
- (8,3)
Exercise \(\PageIndex{5}\)
\(\left\{\begin{array}{l}{7 x+2 y>14} \\ {5 x-y \leq 8}\end{array}\right.\)
- (2,3)
- (7,−1)
- Answer
-
- true
false
Exercise \(\PageIndex{6}\)
\(\left\{\begin{array}{l}{6 x-5 y<20} \\ {-2 x+7 y>-8}\end{array}\right.\)
- (1,−3)
- (−4,4)
Exercise \(\PageIndex{7}\)
\(\left\{\begin{array}{l}{2 x+3 y \geq 2} \\ {4 x-6 y<-1}\end{array}\right.\)
- \(\left(\frac{3}{2}, \frac{4}{3}\right)\)
- \(\left(\frac{1}{4}, \frac{7}{6}\right)\)
- Answer
-
- true
- true
Exercise \(\PageIndex{8}\)
\(\left\{\begin{array}{l}{5 x-3 y<-2} \\ {10 x+6 y>4}\end{array}\right.\)
- \(\left(\frac{1}{5}, \frac{2}{3}\right)\)
- \(\left(-\frac{3}{10}, \frac{7}{6}\right)\)
Solve a System of Linear Inequalities by Graphing
In the following exercises, solve each system by graphing.
Exercise \(\PageIndex{9}\)
\(\left\{\begin{array}{l}{y \leq 3 x+2} \\ {y>x-1}\end{array}\right.\)
- Answer
-
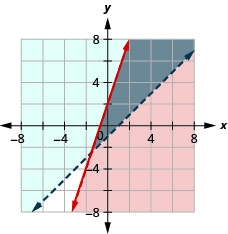
Exercise \(\PageIndex{10}\)
\(\left\{\begin{array}{l}{y<-2 x+2} \\ {y \geq-x-1}\end{array}\right.\)
Exercise \(\PageIndex{11}\)
\(\left\{\begin{array}{l}{y<2 x-1} \\ {y \leq-\frac{1}{2} x+4}\end{array}\right.\)
- Answer
-
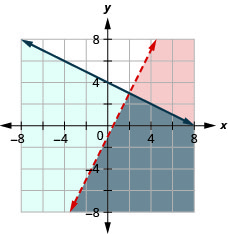
Exercise \(\PageIndex{12}\)
\(\left\{\begin{array}{l}{y \geq-\frac{2}{3} x+2} \\ {y>2 x-3}\end{array}\right.\)
Exercise \(\PageIndex{13}\)
\(\left\{\begin{array}{l}{x-y>1} \\ {y<-\frac{1}{4} x+3}\end{array}\right.\)
- Answer
-
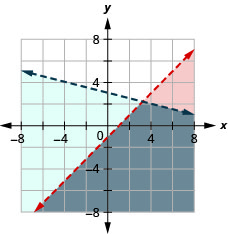
Exercise \(\PageIndex{14}\)
\(\left\{\begin{array}{l}{x+2 y<4} \\ {y<x-2}\end{array}\right.\)
Exercise \(\PageIndex{15}\)
\(\left\{\begin{array}{l}{3 x-y \leq 6} \\ {y \geq-\frac{1}{2} x}\end{array}\right.\)
- Answer
-
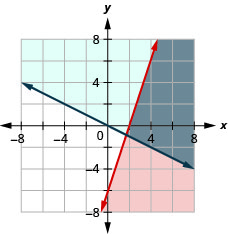
Exercise \(\PageIndex{16}\)
\(\left\{\begin{array}{l}{2 x+4 y \geq 8} \\ {y \leq \frac{3}{4} x}\end{array}\right.\)
Exercise \(\PageIndex{17}\)
\(\left\{\begin{array}{l}{2 x-5 y<10} \\ {3 x+4 y \geq 12}\end{array}\right.\)
- Answer
-
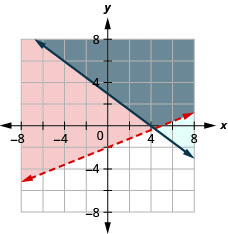
Exercise \(\PageIndex{18}\)
\(\left\{\begin{array}{l}{3 x-2 y \leq 6} \\ {-4 x-2 y>8}\end{array}\right.\)
Exercise \(\PageIndex{19}\)
\(\left\{\begin{array}{l}{2 x+2 y>-4} \\ {-x+3 y \geq 9}\end{array}\right.\)
- Answer
-
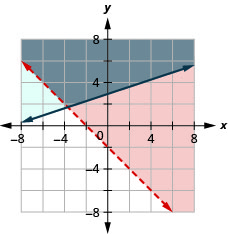
Exercise \(\PageIndex{20}\)
\(\left\{\begin{array}{l}{2 x+y>-6} \\ {-x+2 y \geq-4}\end{array}\right.\)
Exercise \(\PageIndex{21}\)
\(\left\{\begin{array}{l}{x-2 y<3} \\ {y \leq 1}\end{array}\right.\)
- Answer
-
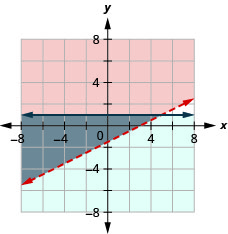
Exercise \(\PageIndex{22}\)
\(\left\{\begin{array}{l}{x-3 y>4} \\ {y \leq-1}\end{array}\right.\)
Exercise \(\PageIndex{23}\)
\(\left\{\begin{array}{l}{y \geq-\frac{1}{2} x-3} \\ {x \leq 2}\end{array}\right.\)
- Answer
-
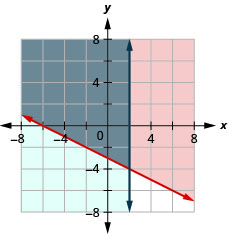
Exercise \(\PageIndex{24}\)
\(\left\{\begin{array}{l}{y \leq-\frac{2}{3} x+5} \\ {x \geq 3}\end{array}\right.\)
Exercise \(\PageIndex{25}\)
\(\left\{\begin{array}{l}{y \geq \frac{3}{4} x-2} \\ {y<2}\end{array}\right.\)
- Answer
-
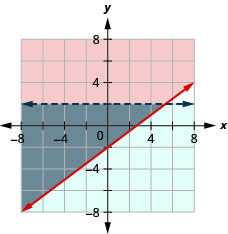
Exercise \(\PageIndex{26}\)
\(\left\{\begin{array}{l}{y \leq-\frac{1}{2} x+3} \\ {y<1}\end{array}\right.\)
Exercise \(\PageIndex{27}\)
\(\left\{\begin{array}{l}{3 x-4 y<8} \\ {x<1}\end{array}\right.\)
- Answer
-
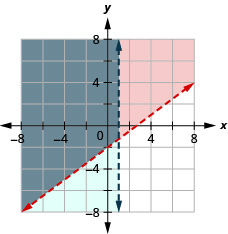
Exercise \(\PageIndex{28}\)
\(\left\{\begin{array}{l}{-3 x+5 y>10} \\ {x>-1}\end{array}\right.\)
Exercise \(\PageIndex{29}\)
\(\left\{\begin{array}{l}{x \geq 3} \\ {y \leq 2}\end{array}\right.\)
- Answer
-
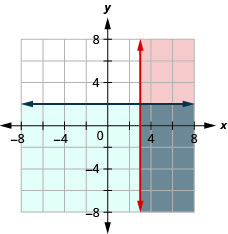
Exercise \(\PageIndex{30}\)
\(\left\{\begin{array}{l}{x \leq-1} \\ {y \geq 3}\end{array}\right.\)
Exercise \(\PageIndex{31}\)
\(\left\{\begin{array}{l}{2 x+4 y>4} \\ {y \leq-\frac{1}{2} x-2}\end{array}\right.\)
- Answer
-
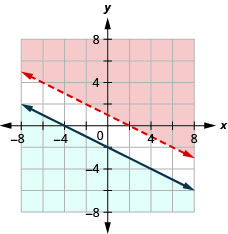
Exercise \(\PageIndex{32}\)
\(\left\{\begin{array}{l}{x-3 y \geq 6} \\ {y>\frac{1}{3} x+1}\end{array}\right.\)
Exercise \(\PageIndex{33}\)
\(\left\{\begin{array}{l}{-2 x+6 y<0} \\ {6 y>2 x+4}\end{array}\right.\)
- Answer
-
No solution
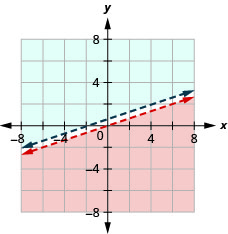
Exercise \(\PageIndex{34}\)
\(\left\{\begin{array}{l}{-3 x+6 y>12} \\ {4 y \leq 2 x-4}\end{array}\right.\)
Exercise \(\PageIndex{35}\)
\(\left\{\begin{array}{l}{y \geq-3 x+2} \\ {3 x+y>5}\end{array}\right.\)
- Answer
-
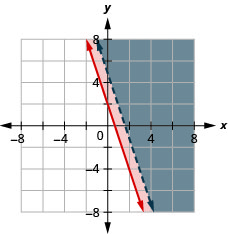
Exercise \(\PageIndex{36}\)
\(\left\{\begin{array}{l}{y \geq \frac{1}{2} x-1} \\ {-2 x+4 y \geq 4}\end{array}\right.\)
Exercise \(\PageIndex{37}\)
\(\left\{\begin{array}{l}{y \leq-\frac{1}{4} x-2} \\ {x+4 y<6}\end{array}\right.\)
- Answer
-
x+4y<6
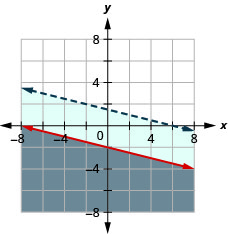
Exercise \(\PageIndex{38}\)
\(\left\{\begin{array}{l}{y \geq 3 x-1} \\ {-3 x+y>-4}\end{array}\right.\)
Exercise \(\PageIndex{39}\)
\(\left\{\begin{array}{l}{3 y>x+2} \\ {-2 x+6 y>8}\end{array}\right.\)
- Answer
-
\(-2 x+6 y>8\)
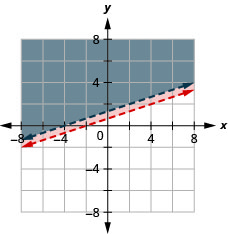
Exercise \(\PageIndex{40}\)
\(\left\{\begin{array}{l}{y<\frac{3}{4} x-2} \\ {-3 x+4 y<7}\end{array}\right.\)
Solve Applications of Systems of Inequalities
In the following exercises, translate to a system of inequalities and solve.
Exercise \(\PageIndex{41}\)
Caitlyn sells her drawings at the county fair. She wants to sell at least 60 drawings and has portraits and landscapes. She sells the portraits for $15 and the landscapes for $10. She needs to sell at least $800 worth of drawings in order to earn a profit.
- Write a system of inequalities to model this situation.
- Graph the system.
- Will she make a profit if she sells 20 portraits and 35 landscapes?
- Will she make a profit if she sells 50 portraits and 20 landscapes?
- Answer
-
- \(\left\{\begin{array}{l}{p+l \geq 60} \\ {15 p+10 l \geq 800}\end{array}\right.\)
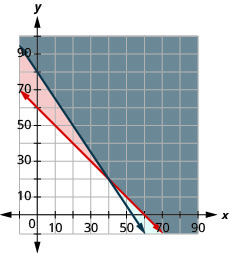
3. No
4. Yes
Exercise \(\PageIndex{42}\)
Jake does not want to spend more than $50 on bags of fertilizer and peat moss for his garden. Fertilizer costs $2 a bag and peat moss costs $5 a bag. Jake’s van can hold at most 20 bags.
- Write a system of inequalities to model this situation.
- Graph the system.
- Can he buy 15 bags of fertilizer and 4 bags of peat moss?
- Can he buy 10 bags of fertilizer and 10 bags of peat moss?
Exercise \(\PageIndex{43}\)
Reiko needs to mail her Christmas cards and packages and wants to keep her mailing costs to no more than $500. The number of cards is at least 4 more than twice the number of packages. The cost of mailing a card (with pictures enclosed) is $3 and for a package the cost is $7.
- Write a system of inequalities to model this situation.
- Graph the system.
- Can she mail 60 cards and 26 packages?
- Can she mail 90 cards and 40 packages?
- Answer
-
- \(\left\{\begin{array}{l}{7 p+3 c \leq 500} \\ {p \geq 2 c+4}\end{array}\right.\)
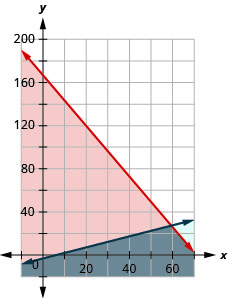
3. Yes
4. No
Exercise \(\PageIndex{44}\)
Juan is studying for his final exams in Chemistry and Algebra. He knows he only has 24 hours to study, and it will take him at least three times as long to study for Algebra than Chemistry.
- Write a system of inequalities to model this situation.
- Graph the system.
- Can he spend 4 hours on Chemistry and 20 hours on Algebra?
- Can he spend 6 hours on Chemistry and 18 hours on Algebra?
Exercise \(\PageIndex{45}\)
Jocelyn is pregnant and needs to eat at least 500 more calories a day than usual. When buying groceries one day with a budget of $15 for the extra food, she buys bananas that have 90 calories each and chocolate granola bars that have 150 calories each. The bananas cost $0.35 each and the granola bars cost $2.50 each.
- Write a system of inequalities to model this situation.
- Graph the system.
- Could she buy 5 bananas and 6 granola bars?
- Could she buy 3 bananas and 4 granola bars?
- Answer
-
- \(\left\{\begin{array}{l}{90 b+150 g \geq 500} \\ {0.35 b+2.50 g \leq 15}\end{array}\right.\)
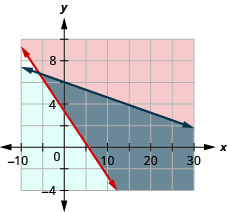
3. No
4. Yes
Exercise \(\PageIndex{46}\)
Mark is attempting to build muscle mass and so he needs to eat at least an additional 80 grams of protein a day. A bottle of protein water costs $3.20 and a protein bar costs $1.75. The protein water supplies 27 grams of protein and the bar supplies 16 gram. If he has $ 10 dollars to spend
- Write a system of inequalities to model this situation.
- Graph the system.
- Could he buy 3 bottles of protein water and 1 protein bar?
- Could he buy no bottles of protein water and 5 protein bars?
Exercise \(\PageIndex{47}\)
Jocelyn desires to increase both her protein consumption and caloric intake. She desires to have at least 35 more grams of protein each day and no more than an additional 200 calories daily. An ounce of cheddar cheese has 7 grams of protein and 110 calories. An ounce of parmesan cheese has 11 grams of protein and 22 calories.
- Write a system of inequalities to model this situation.
- Graph the system.
- Could she eat 1 ounce of cheddar cheese and 3 ounces of parmesan cheese?
- Could she eat 2 ounces of cheddar cheese and 1 ounce of parmesan cheese?
- Answer
-
- \(\left\{\begin{array}{l}{7 c+11 p \geq 35} \\ {110 c+22 p \leq 200}\end{array}\right.\)
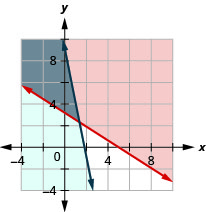
3. Yes
4. No
Exercise \(\PageIndex{48}\)
Mark is increasing his exercise routine by running and walking at least 4 miles each day. His goal is to burn a minimum of 1,500 calories from this exercise. Walking burns 270 calories/mile and running burns 650 calories.
- Write a system of inequalities to model this situation.
- Graph the system.
- Could he meet his goal by walking 3 miles and running 1 mile?
- Could he meet his goal by walking 2 miles and running 2 mile?
Everyday Math
Exercise \(\PageIndex{49}\)
Tickets for an American Baseball League game for 3 adults and 3 children cost less than $75, while tickets for 2 adults and 4 children cost less than $62.
- Write a system of inequalities to model this problem.
- Graph the system.
- Could the tickets cost $20 for adults and $8 for children?
- Could the tickets cost $15 for adults and $5 for children?
- Answer
-
- \(\left\{\begin{array}{l}{3 a+3 c<75} \\ {2 a+4 c<62}\end{array}\right.\
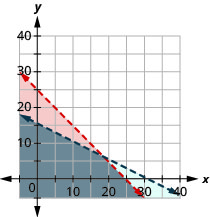
3. No
4. Yes
Exercise \(\PageIndex{50}\)
Grandpa and Grandma are treating their family to the movies. Matinee tickets cost $4 per child and $4 per adult. Evening tickets cost $6 per child and $8 per adult. They plan on spending no more than $80 on the matinee tickets and no more than $100 on the evening tickets.
- Write a system of inequalities to model this situation.
- Graph the system.
- Could they take 9 children and 4 adults to both shows?
- Could they take 8 children and 5 adults to both shows?
Writing Exercises
Exercise \(\PageIndex{51}\)
Graph the inequality \(x-y \geq 3 .\) How do you know which side of the line \(x-y=3\) should be shaded?
- Answer
-
Answers will vary.
Exercise \(\PageIndex{52}\)
Graph the system \(\left\{\begin{array}{l}{x+2 y \leq 6} \\ {y \geq-\frac{1}{2} x-4}\end{array}\right. .\) What does the solution mean?
Self Check
a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
b. After reviewing this checklist, what will you do to become confident for all objectives?


