Practice Makes Perfect
Use the Commutative and Associative Properties
In the following exercises, simplify.
1. \(43m+(−12n)+(−16m)+(−9n)\)
- Answer
-
\(27m+(−21n)\)
2. \(−22p+17q+(−35p)+(−27q)\)
3. \(\frac{3}{8}g+\frac{1}{12}h+\frac{7}{8}g+\frac{5}{12}h\)
- Answer
-
\(\frac{5}{4}g+\frac{1}{2}h\)
4. \(\frac{5}{6}a+\frac{3}{10}b+\frac{1}{6}a+\frac{9}{10}b\)
5. \(6.8p+9.14q+(−4.37p)+(−0.88q)\)
- Answer
-
\(2.43p+8.26q\)
6. \(9.6m+7.22n+(−2.19m)+(−0.65n)\)
7. \(−24·7·\frac{3}{8}\)
- Answer
-
\(−63\)
8. \(−36·11·\frac{4}{9}\)
9. \(\left(\frac{5}{6}+\frac{8}{15}\right)+\frac{7}{15}\)
- Answer
-
\(1\frac{5}{6}\)
10. \(\left(\frac{11}{12}+\frac{4}{9}\right)+\frac{5}{9}\)
11. \(17(0.25)(4)\)
- Answer
-
\(17\)
13. \([2.48(12)](0.5)\)
- Answer
-
\(14.88\)
15. \(12\left(\frac{5}{6}p\right)\)
- Answer
-
\(10p\)
16. \(20\left(\frac{3}{5}q\right)\)
Use the Properties of Identity, Inverse and Zero
In the following exercises, simplify.
17. \(19a+44−19a\)
- Answer
-
\(44\)
19. \(\frac{1}{2}+\frac{7}{8}+\left(−\frac{1}{2}\right)\)
- Answer
-
\(\frac{7}{8}\)
20. \(\frac{2}{5}+\frac{5}{12}+\left(−\frac{2}{5}\right)\)
21. \(10(0.1d)\)
- Answer
-
\(d\)
23. \(\frac{3}{20}·\frac{49}{11}·\frac{20}{3}\)
- Answer
-
\(\frac{49}{11}\)
24. \(\frac{13}{18}·\frac{25}{7}·\frac{18}{13}\)
25. \(\frac{0}{u−4.99}\), where \(u\neq 4.99\)
- Answer
-
\(0\)
26. \(0÷(y−\frac{1}{6})\), where \(x \neq 16\)
27. \(\frac{32−5a}{0}\), where \(32−5a\neq 0\)
- Answer
-
undefined
28. \(\frac{28−9b}{0}\), where \(28−9b\neq 0\)
29. \(\left(\frac{3}{4}+\frac{9}{10}m\right)÷0\), where \(\frac{3}{4}+\frac{9}{10}m\neq 0\)
- Answer
-
undefined
30. \(\left(\frac{5}{16}n−\frac{3}{7}\right)÷0\), where \(\frac{5}{16}n−\frac{3}{7}\neq 0\)
Simplify Expressions Using the Distributive Property
In the following exercises, simplify using the Distributive Property.
31. \(8(4y+9)\)
- Answer
-
\(32y+72\)
33. \(6(c−13)\)
- Answer
-
\(6c−78\)
35. \(\frac{1}{4}(3q+12)\)
- Answer
-
\(\frac{3}{4}q+3\)
36. \(\frac{1}{5}(4m+20)\)
37. \(9(\frac{5}{9}y−\frac{1}{3})\)
- Answer
-
\(5y−3\)
38. \(10(\frac{3}{10}x−\frac{2}{5})\)
39. \(12(\frac{1}{4}+\frac{2}{3}r)\)
- Answer
-
\(3+8r\)
40. \(12(\frac{1}{6}+\frac{3}{4}s)\)
41. \(15⋅\frac{3}{5}(4d+10)\)
- Answer
-
\(36d+90\)
42. \(18⋅\frac{5}{6}(15h+24)\)
43. \(r(s−18)\)
- Answer
-
\(rs−18r\)
45. \((y+4)p\)
- Answer
-
\(yp+4p\)
47. \(−7(4p+1)\)
- Answer
-
\(−28p−7\)
49. \(−3(x−6)\)
- Answer
-
\(−3x+18\)
51. \(−(3x−7)\)
- Answer
-
\(−3x+7\)
53. \(16−3(y+8)\)
- Answer
-
\(−3y−8\)
55. \(4−11(3c−2)\)
- Answer
-
\(−33c+26\)
57. \(22−(a+3)\)
- Answer
-
\(−a+19\)
59. \((5m−3)−(m+7)\)
- Answer
-
\(4m−10\)
61. \(9(8x−3)−(−2)\)
- Answer
-
\(72x−25\)
63. \(5(2n+9)+12(n−3)\)
- Answer
-
\(22n+9\)
65. \(14(c−1)−8(c−6)\)
- Answer
-
\(6c+34\)
67. \(6(7y+8)−(30y−15)\)
- Answer
-
\(12y+63\)
Self Check
a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
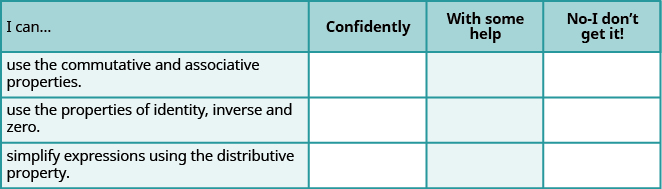
b. After reviewing this checklist, what will you do to become confident for all objectives?



