0.1e: Exercises - Real Number Operations
- Page ID
- 38206
A: The Number Line, Set and Interval Notation
Exercises \(\PageIndex{1}\)
\( \bigstar \) Graph the solution set and give the interval notation and set-builder notation equivalents.
|
1. \(x<−1\) 2. \(x>−3\) 3. \(x\geq −8\) 4. \(x\leq 6\) |
5. \(−10\leq x<4\) 6. \(3<x\leq 7\) 7. \(−40<x<0\) 8. \(−12\leq x\leq −4\) |
9. \(x<5\) and \(x\geq 0\) 10. \(x\leq −10\) and \(x\geq −40\) 11. \(x\leq 7\) and \(x<10\) 12. \(x<1\) and \(x>3\) |
13. \(x<−2\) or \(x\geq 5\) 14. \(x\leq 0\) or \(x\geq 4\) 15. \(x<6\) or \(x>2\) 16. \(x<0\) or \(x\leq 5\) |
- Answers to odd exercises:
-
1. \((−∞, −1)\); \(\{x| \, x<−1\}\);
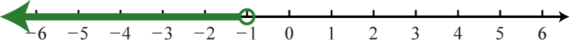
Figure 0.1e.1 3. \([−8,∞)\); \(\{x| \, x \geq −8\}\);

Figure 0.1e.3 5. \([−10,4)\); \(\{x|−10≤x<4\}\);

Figure 0.1e.5 7. \((−40,0)\); \(\{x|−40<x<0\}\);

Figure 0.1e.7 9. \([0,5)\); \(\{x| \, 0≤x<5\}\);

Figure 0.1e.9 11. \((−∞,7]\); \(\{x| \, x \le 7\}\);

Figure 0.1e.11 13. \((−∞,−2)\cup [5,∞)\); \(\{x| \, x<−2 \text{ or } x \geq 5\}\)
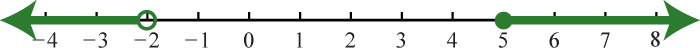
Figure 0.1e.13 15. \((−∞,∞)=\mathbb{R}\);

Figure 0.1e.15
B: Convert a Description to an Inequality
Exercises \(\PageIndex{2}\)
\( \bigstar \) Write an equivalent inequality.
|
17. All real numbers less than \(−15\). 18. All real numbers greater than or equal to \(−7\). 19. All real numbers less than \(6\) and greater than zero. |
20. All real numbers less than zero and greater than \(−5\). 21. All real numbers less than or equal to \(5\) or greater than \(10\). 22. All real numbers between \(−2\) and \(2\). |
- Answers to odd exercises:
-
17. \(x<−15\) 19. \(0<x<6\) 21. \(x\leq 5\) or \(x>10\)
C: Convert Interval Notation to an Inequality
Exercises \(\PageIndex{3}\)
\( \bigstar \) Determine the inequality given the answers expressed in interval notation.
|
23. \((−∞,12)\) 24. \([−8,∞)\) 25. \((−∞,0]\) |
26. \((0,∞)\) 27. \((−6,14)\) 28. \((0,12]\) |
29. \([5,25)\) 30. \([−30,−10]\) 31. \((−∞,2)\cup [3,∞)\) |
32. \((−∞,−19]\cup [−12,∞)\) 33. \((−∞,−2)\cup (0,∞)\) 34. \((−∞,−15]\cup (−5,∞)\) |
- Answers to odd exercises:
-
23. \(x<12\)
25. \(x\leq 0\)27. \(−6<x<14\)
29. \(5\leq x<25\)31. \(x<2\) or \(x\geq 3\)
33. \(x<−2\) or \(x>0\)
D: Order of Operations
Exercises \(\PageIndex{4}\)
\( \bigstar \) Use order of operations to evaluate the given expression.
|
36. 10+2×(5−3) 37. 6÷2−(81÷32) 38. 18+(6−8)3 39. −2×[16÷(8−4)2]2 40. 4−6+2×7 41. 3(5−8) |
42. 4+6−10÷2 43. 12÷(36÷9)+6 44. (4+5)2÷3 45. 3−12×2+19 46. 2+8×7÷4 47. 5+(6+4)−11 |
48. 9−18÷32 49. 14×3÷7−6 50. 9−(3+11)×2 51. 6+2×2−1 52. 64÷(8+4×2) 53. 9+4(22) |
54. (12÷3×3)2 55. 25÷52−7 56. (15−7)×(3−7) 57. 2×4−9(−1) 58. \(4^{2} - 25 \cdot \frac{1}{5}\) 59. 12(3−1)÷6 |
- Answers to odd exercises:
-
37. −6 \(\qquad\)39. −2 \(\qquad\)41. −9 \(\qquad\)43. 9 \(\qquad\)45. −2 \(\qquad\)47. 4
49. 0 \(\qquad\)51. 9 \(\qquad\)53. 25 \(\qquad\)55. −6 \(\qquad\)57. 17 \(\qquad\)59. 4
E: Substitute and Evaluate Expressions
Exercises \(\PageIndex{5}\)
\( \bigstar \) Evaluate.
|
61. \(−2x + 3\) where \(x = −2\) 62. \(8x − 5\) where \(x = −1\) 63. \(x^{2} − x + 5\) where \(x = −5\) 64. \(2x^{2} − 8x + 1\) where \(x = 3\) 65. \(\dfrac { x ^ { 2 } - x + 2 } { 2 x - 1 }\) where \(x = -\frac{1}{2}\) 66. \(\dfrac { 9 x ^ { 2 } + x - 2 } { 3 x - 4 }\) where \(x = -\frac{2}{3}\) 67. \(( 3 y - 2 ) ( y + 5 )\) where \(y = \frac { 2 } { 3 }\) 68. \((3x + 2) (5x + 1)\) where \(x = −\frac{1}{5}\) 69. \((3x − 1) (x − 8)\) where \(x = −1\) |
70. \((7y + 5) (y + 1)\) where \(y = −2\) 71. \(y^{6} − y^{3} + 2\) where \(y = −1\) 72. \(y^{5} + y^{3} − 3\) where \(y = −2\) 73. \(a^{2} − 5b^{2}\) where \(a = −2\) and \(b = −1\) 74. \(a^{3} − 2b^{3}\) where \(a = −3\) and \(b = 2\) 75. \((x − 2y) (x + 2y)\) where \(x = 2\) and \(y = −5\) 76. \((4x − 3y) (x − y)\) where \(x = −4\) and \(y = −3\) 77. \(a^{2} − ab + b^{2}\) where \(a = −1\) and \(b = −2\) 78. \(x^{2}y^{2} − xy + 2\) where \(x = −3\) and \(y = −2\) 79. \(a^{4} − b^{4}\) where \(a = −2\) and \(b = −3\) 80. \(a^{6} − 2a^{3}b^{3} − b^{6}\) where \(a = 2\) and \(b = −1\) |
81. Evaluate \( \sqrt { b^2 - 4 a c }\) given the following values.
|
a. \(a = 6, b = 1\) and \(c = −1\) b. \(a = 15, b = 4\) and \(c = −4\) c. \(a = \dfrac{3}{4} , b = −2\) and \(c = −4\) |
d. \(a = \dfrac{1}{2} , b = −2\) and \(c = −30\) e. \(a = 1, b = 2\) and \(c = −1\) f. \(a = 1, b = −4\) and \(c = −50\) |
g. \(a = 1, b = −1\) and \(c = −\dfrac{1}{16}\) h. \(a = −2, b = −\dfrac{1}{3}\) and \(c = 1\) |
- Answers to odd exercises:
-
61. \(7\) \(\qquad\) 63. \(35\) \(\qquad\) 65. \(−\frac{11}{8}\) \(\qquad\) 67. \(0\) \(\qquad\) 69. \(36\) \(\qquad\) 71. \(4\) \(\qquad\) 73. \(−1\) \(\qquad\)
75. \(−96\) \(\qquad\) 77. \(3\) \(\qquad\) 79. \(−65\) \(\qquad\) 81 a. \(5\) \(\qquad\) 81 c. \(4\) \(\qquad\) 81 e. \(2\sqrt{2}\) \(\qquad\) 81 g. \(\frac { \sqrt { 5 } } { 2 }\)
F: Simplify Algebraic Expressions
Exercises \(\PageIndex{6}\)
\( \bigstar \) Simplify.
|
85. \(5 − 2 (4x + 8)\) 86. \(8 − 6 (2x − 1)\) 87. \(2 (x^{2} − 7x + 1) + 3x − 7\) 88. \(−5 (x^{2} + 4x − 1) + 8x^{2} − 5\) 89. \(5ab − 4 (ab + 5)\) 90. \(5 (7 − ab) + 2ab\) 91. \(2 − a^{2} + 3 (a^{2} + 4)\) 92. \(7 − 3y + 2 (y^{2} − 3y − 2)\) 93. \(8x^{2} − 3x − 5 (x^{2} + 4x − 1)\) 94. \(2 − 5y − 6 (y^{2} − y + 2)\) 95. \(a^{2}b^{2} − 5 + 3 (a^{2}b^{2} − 3ab + 2)\) |
96. \(a^{2} − 3ab − 2 (a^{2} − ab + 1)\) 97. \(10y^{2} + 6 − (3y^{2} + 2y + 4)\) 98. \(4m^{2} − 3mn − (m^{2} − 3mn + n^{2} )\) 99. \(x^{2n} − 3x^{n} + 5 (x^{2n} − x^{n} + 1)\) 100. \(−3 (y^{2n} − 2y^{n} + 1) + 4y^{2n} − 5\) 101. \( 7x - x \div 2 \times 4 + \dfrac{x}{3} \) 102. \(5v \div 3v \times (9-6+2) \) 103. \(7z - 3 + z \times 6^2 \) 104. \( 4 \times 3 + 18 x \div 9 - 12 \) 105. \( 8b -1 - 4b \times 3 + 2\) 106. \( a \div 64 \times 2^3 -12a \div 6\) |
107. \(27 -(4)^2 y-11 \) 108. \(4x + x(13-7) \) 109. \( 9(y + 8) - 27 \) 110. \( \Big{(} \displaystyle \frac{9}{6}t−4 \Big{)}2\) 111. \( 6 + 12b - 3 (6b) \) 112. \( 18y - 2(1 + 7y) \) 113. \( \Big{(} \displaystyle \frac{4}{9} \Big{)} ^{2} 27x \) 114. \( 8(3 - m) + 1(-8) \) 115. \( 9x + 4x(2 + 3) - 4(2x + 3x) \) 116. \( 5^2 - 4(3x) \) |
- Answers to odd exercises:
-
85. \(−8x − 11\) \( \qquad \) 87. \(2x^{2} − 11x − 5\) \( \qquad \) 89. \(ab − 20\) \( \qquad \) 91. \(2a^{2} + 14\) \( \qquad \) 93. \(3x^{2} − 23x + 5\) \( \qquad \)
95. \(4a^{2}b^{2} − 9ab + 1\) \( \qquad \) 97. \(7y^{2} − 2y + 2\) \( \qquad \) 99. \(6x^{2n} − 8x^{n} + 5\) \( \qquad \) 101. \( \frac{16x}{3} \) \( \qquad\) 103. \(43z-3 \)
105. \(-4b+1\) \( \qquad \) 107. \( -14y-11\) \( \qquad \) 109. \(9y+45 \) 111. \( -6b+6 \)\( \qquad \) 113. \( \frac{16x}{3} \) \( \qquad \) 115. \(9x \)

