Skip to main content
Mathematics LibreTexts

0.8e: Exercises- Linear Inequalities

  1. Last updated
  2. Save as PDF
  • Page ID
    38278

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    A: Check a solution

    Exercise \(\PageIndex{1}\) 

    \( \bigstar \)  Determine whether or not the given value is a solution.

    1. \(5 x - 1 < - 2 ; x = - 1\)
    2. \(- 3 x + 1 > - 10 ; x = 1\)
    3. \(2 x - 3 < - 5 ; x = 1\)
    4. \(5 x - 7 < 0 ; x = 2\)
    1. \(9 y - 4 \geq 5 ; y = 1\)
    2. \(- 6 y + 1 \leq 3 ; y = - 1\)
    3. \(12 a + 3 \leq - 2 ; a = - \dfrac { 1 } { 3 }\)
    1. \(25 a - 2 \leq - 22 ; a = - \dfrac { 4 } { 5 }\)
    2. \(- 10 < 2 x - 5 < - 5 ; x = - \dfrac { 1 } { 2 }\)
    3. \(3 x + 8 < - 2 \text { or } 4 x - 2 > 5 ; x = 2\)
    Answers to odd exercises:
    1. Yes 3. No 5. Yes 7. No 9. Yes

    B: Solve Linear Inequalities

    Exercise \(\PageIndex{2}\) 

    \( \bigstar \)  Graph all solutions on a number line and provide the corresponding interval notation.

    1. \(3 x + 5 > - 4\)
    2. \(2 x + 1 > - 1\)
    3. \(5 - 6 y < - 1\)
    4. \(7 - 9 y > 43\)
    5. \(6 - a \leq 6\)
    6. \(- 2 a + 5 > 5\)
    7. \(\dfrac { 5 x + 6 } { 3 } \leq 7\)
    8. \(\dfrac { 4 x + 11 } { 6 } \leq \dfrac { 1 } { 2 }\)
    9. \(\dfrac { 1 } { 2 } y + \dfrac { 5 } { 4 } \geq \dfrac { 1 } { 4 }\)
    10. \(\dfrac { 1 } { 12 } y + \dfrac { 2 } { 3 } \leq \dfrac { 5 } { 6 }\)
    11. \(2 ( 3 x + 14 ) < - 2\)
    1. \(5 ( 2 y + 9 ) > - 15\)
    2. \(5 - 2 ( 4 + 3 y ) \leq 45\)
    3. \(- 12 + 5 ( 5 - 2 x ) < 83\)
    4. \(6 ( 7 - 2 a ) + 6 a \leq 12\)
    5. \(2 a + 10 ( 4 - a ) \geq 8\)
    6. \(9 ( 2 t - 3 ) - 3 ( 3 t + 2 ) < 30\)
    7. \(- 3 ( t - 3 ) - ( 4 - t ) > 1\)
    8. \(\dfrac { 1 } { 2 } ( 5 x + 4 ) + \dfrac { 5 } { 6 } x > - \dfrac { 4 } { 3 }\)
    9. \(\dfrac { 2 } { 5 } + \dfrac { 1 } { 6 } ( 2 x - 3 ) \geq \dfrac { 1 } { 15 }\)
    10. \(5 x - 2 ( x - 3 ) < 3 ( 2 x - 1 )\)
    11. \(3 ( 2 x - 1 ) - 10 > 4 ( 3 x - 2 ) - 5 x\)
    1. \(- 3 y \geq 3 ( y + 8 ) + 6 ( y - 1 )\)
    2. \(12 \leq 4 ( y - 1 ) + 2 ( 2 y + 1 )\)
    3. \(- 2 ( 5 t - 3 ) - 4 > 5 ( - 2 t + 3 )\)
    4. \(- 7 ( 3 t - 4 ) > 2 ( 3 - 10 t ) - t\)
    5. \(\dfrac { 1 } { 2 } ( x + 5 ) - \dfrac { 1 } { 3 } ( 2 x + 3 ) > \dfrac { 7 } { 6 } x + \dfrac { 3 } { 2 }\)
    6. \(- \dfrac { 1 } { 3 } ( 2 x - 3 ) + \dfrac { 1 } { 4 } ( x - 6 ) \geq \dfrac { 1 } { 12 } x - \dfrac { 5 } { 4 }\)
    7. \(4 ( 3 x + 4 ) \geq 3 ( 6 x + 5 ) - 6 x\)
    8. \(1 - 4 ( 3 x + 7 ) < - 3 ( x + 9 ) - 9 x\)
    9. \(6 - 3 ( 2 a - 1 ) \leq 4 ( 3 - a ) + 1\)
    10. \(12 - 5 ( 2 a + 6 ) \geq 2 ( 5 - 4 a ) - a\)
    Answers to odd exercises:

    11. \(( - 3 , \infty )\);

    a2d07ff66453c86a51eb9ee5ca94a731.png

    Figure 1.8.11

    13. \(( 1 , \infty )\);

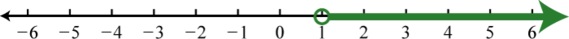
    4c6582dd8bfda422448899007c16d724.png
    Figure 0.8e.13

    15. \([ 0 , \infty )\);

    b071e41cd81d51aa4ebb4a13391c3cd2.png
    Figure 0.8e.15

    17. \(( - \infty , 3 ]\);

    91d267fa92ccb40b4595195880f91df6.png
    Figure 0.8e.17

    19. \([ - 2 , \infty )\);

    d153c7b86b8dc29e176a29ab877b331d.png
    Figure 0.8e.19

    21. \(( - \infty , - 5 )\);

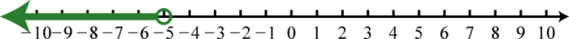
    2a7c54ebfc233db09481bb0a0bf08196.png
    Figure 0.8e.21

    23. \([ - 8 , \infty )\);

    54e6dff73772146a09c04377ddc207f5.png
    Figure 0.8e.23

    25. \([ 5 , \infty )\);

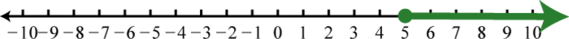
    03409a368549dec8586478a428d6ae3e.png
    Figure 0.8e.25

    27. \(( - \infty , 7 )\);

    ce9a2a9cde8d1177dd584f5d23b38e8d.png
    Figure 0.8e.27

    29. \(( - 1 , \infty )\);

    2808e08ce9edb2c71679d77495f807e5.png
    Figure 0.8e.29

    31. \(( 3 , \infty )\);

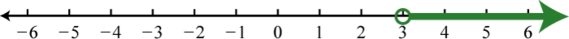
    46ffae560a1c8ea849b82a0d2ad14469.png
    Figure 0.8e.31

    33. \(\left( - \infty , - \dfrac { 3 } { 2 } \right]\);

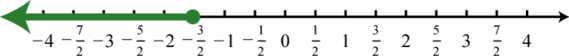
    8a7dbeaa313712aed9d1259e063e7315.png
    Figure 0.8e.33

    35. \(\emptyset\);

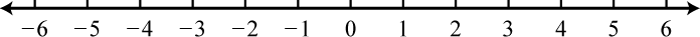
    2d80488891eff5ced515c44f960d3f60.png
    Figure 0.8e.35

    37. \(( - \infty , 0 )\);

    b77844f950f5a2314de7266b49e9f47e.png
    Figure 0.8e.37

    39. \(\mathbb { R }\);

    dfcf1b7d9dadca607c621c6670858ce7.png
    Figure 0.8e.39

    41. \([ - 2 , \infty )\);

    75c310d02f109355854102f8d79fae68.png
    Figure 0.8e.41

    C: Solve Compound Linear Inequalities

    Exercise \(\PageIndex{3}\) 

    \( \bigstar \)  Graph all solutions on a number line and provide the corresponding interval notation.

    1. \(- 1 < 2 x + 1 < 9\)
    2. \(- 4 < 5 x + 11 < 16\)
    3. \(- 7 \leq 6 y - 7 \leq 17\)
    4. \(- 7 \leq 3 y + 5 \leq 2\)
    5. \(- 7 < \dfrac { 3 x + 1 } { 2 } \leq 8\)
    6. \(- 1 \leq \dfrac { 2 x + 7 } { 3 } < 1\)
    7. \(- 4 \leq 11 - 5 t < 31\)
    8. \(15 < 12 - t \leq 16\)
    9. \(- \dfrac { 1 } { 3 } \leq \dfrac { 1 } { 6 } a + \dfrac { 1 } { 3 } \leq \dfrac { 1 } { 2 }\)
    10. \(- \dfrac { 1 } { 6 } < \dfrac { 1 } { 3 } a + \dfrac { 5 } { 6 } < \dfrac { 3 } { 2 }\)
    11. \(5 x + 2 < - 3 \text { or } 7 x - 6 > 15\)
    12. \(4 x + 15 \leq - 1 \text { or } 3 x - 8 \geq - 11\)
    13. \(8 x - 3 \leq 1 \text { or } 6 x - 7 \geq 8\)
    14. \(6 x + 1 < - 3 \text { or } 9 x - 20 > - 5\)
    1. \(8 x - 7 < 1 \text { or } 4 x + 11 > 3\)
    2. \(10 x - 21 < 9 \text { or } 7 x + 9 \geq 30\)
    3. \(7 + 2 y < 5 \text { or } 20 - 3 y > 5\)
    4. \(5 - y < 5 \text { or } 7 - 8 y \leq 23\)
    5. \(15 + 2 x < - 15 \text { or } 10 - 3 x > 40\)
    6. \(10 - \dfrac { 1 } { 3 } x \leq 5 \text { or } 5 - \dfrac { 1 } { 2 } x \leq 15\)
    7. \(9 - 2 x \leq 15 \text { and } 5 x - 3 \leq 7\)
    8. \(5 - 4 x > 1 \text { and } 15 + 2 x \geq 5\)
    9. \(7 y - 18 < 17 \text { and } 2 y - 15 < 25\)
    10. \(13 y + 20 \geq 7 \text { and } 8 + 15 y > 8\)
    11. \(5 - 4 x \leq 9 \text { and } 3 x + 13 \leq 1\)
    12. \(17 - 5 x \geq 7 \text { and } 4 x - 7 > 1\)
    13. \(9 y + 20 \leq 2 \text { and } 7 y + 15 \geq 1\)
    1. \(21 - 6 y \leq 3 \text { and } - 7 + 2 y \leq - 1\)
    2. \(- 21 < 6 ( x - 3 ) < - 9\)
    3. \(0 \leq 2 ( 2 x + 5 ) < 8\)
    4. \(- 15 \leq 5 + 4 ( 2 y - 3 ) < 17\)
    5. \(5 < 8 - 3 ( 3 - 2 y ) \leq 29\)
    6. \(5 < 5 - 3 ( 4 + t ) < 17\)
    7. \(- 3 \leq 3 - 2 ( 5 + 2 t ) \leq 21\)
    8. \(- 40 < 2 ( x + 5 ) - ( 5 - x ) \leq - 10\)
    9. \(- 60 \leq 5 ( x - 4 ) - 2 ( x + 5 ) \leq 15\)
    10. \(- \dfrac { 1 } { 2 } < \dfrac { 1 } { 30 } ( x - 10 ) < \dfrac { 1 } { 3 }\)
    11. \(- \dfrac { 1 } { 5 } \leq \dfrac { 1 } { 15 } ( x - 7 ) \leq \dfrac { 1 } { 3 }\)
    12. \(- 1 \leq \dfrac { a + 2 ( a - 2 ) } { 5 } \leq 0\)
    13. \(0 < \dfrac { 5 + 2 ( a - 1 ) } { 6 } < 2\)
    Answers to odd exercises:

    43. \((- 1,4 )\);

    d21c3764ee66e2b7f0c11cda361eecd6.png
    Figure 0.8e.43

    45. \([0,4]\);

    c1ef787cbdd913cd00cc57e2e943f2c5.png
    Figure 0.8e.45

    47. \((−5,5]\);

    6e65b13c4fa8424fece5350fffb911a6.png
    Figure 0.8e.47

    49. \((−4,3]\);

    f98dd22751024e52b172b02331df437f.png
    Figure 0.8e.49

    51. \([−4,1]\);

    31307052ff666827bf09f61ce5d2dd67.png
    Figure 0.8e.51

    53. \((−∞,−1)∪(3,∞)\);

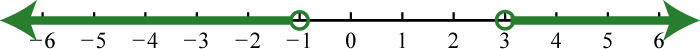
    0bc88715413b651c0c03448735b56907.png
    Figure 0.8e.53

    55. \((−∞,\frac{1}{2}]∪[\frac{5}{2},∞)\);

    8db832ab9f7eff6051818eaf2a44cb7c.png
    Figure 0.8e.55

    57. \(ℝ\);

    dfcf1b7d9dadca607c621c6670858ce7.png
    Figure 0.8e.57

    59. \((−∞,5)\);

    8b2a55ebeb6f310cf5ce1db0935049d1.png
    Figure 0.8e.59

    61. \((−∞,−10)\);

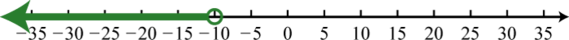
    da06ba5780b2a83855d49588d438223e.png
    Figure 1.8.61

    63. \([−3,2]\);

    ac3f7c2bf437eda365cbeb0d32b85a95.png
    Figure 0.8e.63

    65. \((−∞,5)\);

    8f48a1f8474bc7e6615e94352ea50a23.png
    Figure 0.8e.65

    67. \(Ø\);

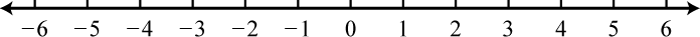
    2d80488891eff5ced515c44f960d3f60.png
    Figure 0.8e.67

    69. \(−2\);

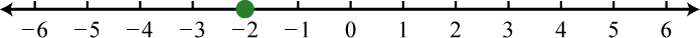
    44f3dc88d9fc576e5c1a02cc592cc371.png
    Figure 0.8e.69

    71. \((−\frac{1}{2},\frac{3}{2})\);

    a26cdc2d0fdc28f73b61e7e78df78f42.png
    Figure 0.8e.71

    73. \([−1,3)\);

    fb3b77aafa12f74752f695c13dc393cd.png
    Figure 0.8e.73

    75. \((−8,−4)\);

    4708d04c65e378bd10e211500e34b237.png
    Figure 0.8e.75

    77. \((−15,−5]\);

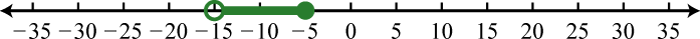
    febc3d6aec89ccf8cbe28675154888e5.png
    Figure 0.8e.77

    79. \((−5,20)\);

    38de268d929f9fddb7936a288714a942.png
    Figure 0.8e.79

    81. \([−\frac{1}{3}, \frac{4}{3}]\);

    a5de4bad28d7e3a3d558d3e6edf70ed9.png
    Figure 0.8e.81

    .

    0.8e: Exercises- Linear Inequalities is shared under a not declared license and was authored, remixed, and/or curated by LibreTexts.

    1. Back to top
    • Was this article helpful?

    Recommended articles

    1. Article type
      Section or Page
      Show Page TOC
      yes
    2. Tags
      This page has no tags.