1.7: Absolute Value Equations and Inequalities

Last updated
Save as PDF

Page ID: 38273

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Solving an Absolute Value Equation

Recall that the absolute value of a real number $a$, denoted $|a|$, is defined as the distance between zero (the origin) and the graph of that real number on the number line. For example, $|−3|=3$ and $|3|=3$.

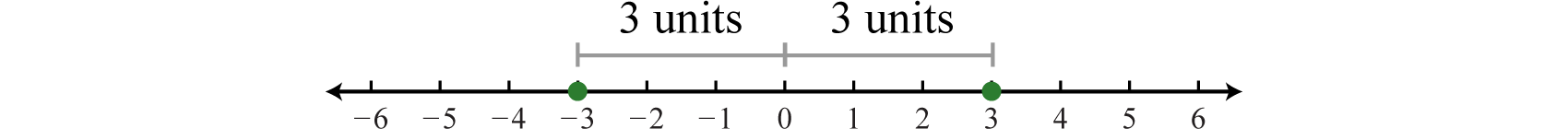
In addition, the absolute value of a real number can be defined algebraically as a piecewise function.

$| a | = \left\{ \begin{array} { l } { a \text { if } a \geq 0 } \\ { - a \text { if } a < 0 } \end{array} \right.$

Given this definition, $|3| = 3$ and $|−3| = − (−3) = 3$.Therefore, the equation $|x| = 3$ has two solutions for $x$, namely $\{±3\}$.

Next, To solve an equation such as $|2x−6|=8$, notice that the absolute value will be equal to $8$ if the quantity inside the absolute value bars is $8$ or $−8$. This leads to two different equations can be solved independently.

$|2x−6|=8$
$ \begin{array} {r|r}
2x-6= 8 & 2x-6= -8 \\
2x= 14 & 2x= -2 \\
x= 7 & x= -1
\end{array} $

Knowing how to solve problems involving absolute value functions is useful. For example, we may need to identify numbers or points on a line that are at a specified distance from a given reference point.

Definition is a green note

Definition: Absolute Value Equations

The absolute value of any algebraic expression $u$, is written as $|u|$ and is never negative, although the argument $u$ inside the absolute value bars can be either positive or negative.
For any real number $c$, the absolute value equation $| u | = c$ has the following properties

If $c<0$, then $|u|=c$ has no solution.
If $c=0$, then $|u|=c$ has one solution.
If $c>0$, then $|u|=c$ has two solutions.

$how-to.png$ Howto: Solve an Absolute Value Equation.

Isolate the absolute value expression $|u|$ on one side of the equal sign, producing an equation of the form $|u|=c$
If $c>0$, write and solve two equations: $u=c$ and $u=−c$.
If $c=0$, solve the single equation: $u=0$
If $c<0$, the equation has no solution.

Example $\PageIndex{1}$: Solving Absolute Value Equations

Solve the following absolute value equations:

$|6x+4|=8$
$ |3x+4| + 7=1 $
$| 2 x + 3 |-1 = 3$
$2 |5x − 1| − 3 = 9$.
$|−5x+10| + 3=3$

Solution:

The absolute value expression is isolated already, so rewrite it as two separate equations and solve them.

$|6x+4|=8$
$ \begin{array} {r|r}
6x+4= 8 & 6x+4= -8 \\
6x= 4 & 6x= -12 \\
x= \dfrac{2}{3} & x= -2 \\
\end{array} $

$ \quad $ The solution set is $ \left\{ \tfrac{2}{3}, -2 \right\} $

Isolate the absolute value expression in the equation.

$ |3x+4| + 7=1 $
$ |3x+4| =-6 $

$ \quad $ An absolute value cannot be negative. Therefore the equation does not have a solution.
$ \quad $ The solution set is $ \{ \:\: \} $

Isolate the absolute value expression in the equation.

$| 2 x + 3 | -1 = 3$
$| 2 x + 3 | = 4$

$ \quad $ Rewrite the absolute value as two separate equations and solve them.

$ \begin{array} {r|r}
2 x + 3 = - 4 & 2 x + 3 = 4 \\
2 x = - 7 & 2 x = 1 \\
- \frac { 7 } { 2 } & x = \frac { 1 } { 2 } \\
\end{array} $

$ \quad $ The solution set is $ \{ - \frac { 7 } { 2 }, \frac { 1 } { 2 } \} $

Isolate the absolute value expression in the equation.

$2 |5x − 1| − 3 = 9$
$2 |5x − 1| = 12$
$ |5x − 1| = 6$

$ \quad $ Rewrite the absolute value as two separate equations and solve them.

$ \begin{array} {r|r}
5 x - 1 = - 6 & 5 x - 1 = 6 \\
5 x = - 5 & 5 x = 7 \\
x = - 1 & x = \frac { 7 } { 5 } \\
\end{array} $

$ \quad $ The solution set is $ \{ -1, \frac { 7 } { 5 } \} $

Isolate the absolute value expression in $|−5x+10| + 3=3$.

$|−5x+10| + 3=3$
$|−5x+10| =0$

$ \quad $ The equation is set equal to zero, so we have to write only one equation.

\[\begin{align*} -5x+10&= 0\\ -5x&= -10\\ x&= 2 \end{align*}\]

$ \quad $ The solution set is $ \{ 2 \} $

$try-it.png$ Try It $\PageIndex{1}$

Solve.

$|1−4x|+8=13$.
$2 - 7 | x + 4 | = - 12$.

Answer: a, $x=−1, x=\dfrac{3}{2}$ $ \qquad $ b. $-6, -2$

If two absolute value expressions are equal, then the arguments can either be the exact same value, or be the exact same value but with opposite signs.

Example $\PageIndex{2}$:

Solve: $| 2 x - 5 | = | x - 4 |$.

Solution

Set $2x-5$ equal to $\pm ( x - 4 )$ and then solve each linear equation.

$\begin{array} { c } { | 2 x - 5 | = | x - 4 | } \\ { 2 x - 5 = - ( x - 4 ) \:\: \text { or }\:\: 2 x - 5 = + ( x - 4 ) } \\ { 2 x - 5 = - x + 4 }\quad\quad\quad 2x-5=x-4 \\ { 3 x = 9 }\quad\quad\quad\quad\quad\quad \quad\quad x=1 \\ { x = 3 \quad\quad\quad\quad\quad\quad\quad\quad\quad\:\:\:\:} \end{array}$

The solution set is $ \{ 1, 3 \} $

$try-it.png$ Try It $\PageIndex{2}$

Solve: $| x + 10 | = | 3 x - 2 |$.

Answer: $-2, 6$

Absolute Value Inequalities

Consider the solutions to the inequality $| x | \leq 3$. The absolute value of a number represents the distance from the origin. Therefore, this inequality describes all numbers whose distance from zero is less than or equal to $3$. We can graph this solution set by shading all such numbers.

This solution set is expressed using set notation or interval notation as follows:

$\begin{array} { c } { \{ x | - 3 \leq x \leq 3 \} \color{Cerulean} { Set\: Notation } } \\ { [ - 3,3 ] \quad \color{Cerulean}{ Interval \:Notation } } \end{array}$

In contrast, examine solutions to the inequality $| x | \geq 3$. This inequality describes all numbers whose distance from the origin is greater than or equal to $3$. On a graph, we can shade all such numbers.

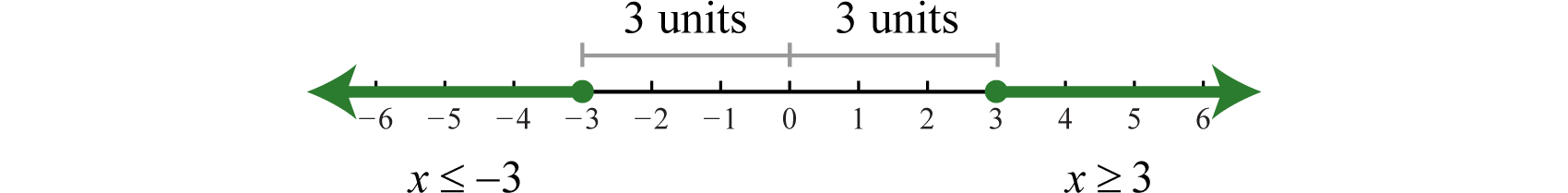
This solution set is expressed using using set notation and interval notation as follows:

$\begin{array} { l } { \{ x | x \leq - 3 \text { or } x \geq 3 \} \:\:\color{Cerulean} { Set\: Notation } } \\ { ( - \infty , - 3 ] \cup [ 3 , \infty ) \:\:\color{Cerulean} { Interval\: Notation } } \end{array}$

$how-to.png$ Howto: Solve a Linear Absolute Value Inequality.

Given an algebraic expression $ u $ and a positive number $c $,

Isolate the absolute value expression $|u|$ on left side of the inequality symbol
The solution of $ | u | < c $ is a single interval composed of the numbers that satisfy the compound inequality $ -c < u < c $.
The solution of $ | u | > c $ is a combination of two separate intervals that satisfy the two separate inequalities $ u < -c $ or $ u > c $. NOTE that $ | u | > c $ CANNOT be written as $ -c < u > c $.
These rules are valid if $ < $ is replaced with $ \le $ and $ > $ is replaced with $ \ge $.

Example $\PageIndex{3}$:

Solve and graph the solution set: $|x+2|<3$.

Solution

The absolute value expression is already isolated. Bound the argument $x+2$ by $−3$ and $3$ in a compound inequality and solve.

$\begin{array} { c } { | x + 2 | < 3 } \\ { - 3 < x + 2 < 3 } \\ { - 3 \color{Cerulean}{- 2}\color{Black}{ <} x + 2 \color{Cerulean}{- 2}\color{Black}{ <} 3 \color{Cerulean}{- 2} } \\ { - 5 < x < 1 } \end{array}$

Here we use open dots to indicate strict inequalities on the graph as follows.

Using interval notation, $(−5,1)$.

Example $\PageIndex{4}$:

Solve: $4 |x + 3| − 7 ≤ 5$.

Solution

Isolate the absolute value expression.

$\begin{array} { c } { 4 | x + 3 | - 7 \leq 5 } \\ { 4 | x + 3 | \leq 12 } \\ { | x + 3 | \leq 3 } \end{array}$

Rewrite the absolute value inequality as a compound inequality and solve.

$\begin{array} { c } { - 3 \leq x + 3 \leq 3 } \end{array}$

$\begin{aligned} - 3 \color{Cerulean}{- 3} \color{Black}{ \leq} x + 3 \color{Cerulean}{- 3} & \color{Black}{ \leq} 3 \color{Cerulean}{- 3} \\ - 6 \leq x \leq 0 \end{aligned}$

Shade the solutions on a number line and present the answer in interval notation. Here we use closed dots to indicate inclusive inequalities on the graph as follows:

Using interval notation, $[−6,0]$

$try-it.png$ Try It $\PageIndex{4}$

Solve and graph the solution set: $3 + | 4 x - 5 | < 8$.

Answer: Interval notation: $(0, \frac{5}{2})$

$53fbc057eea3477b5709c94560299f26.png$

Example $\PageIndex{5}$:

Solve and graph the solution set: $|x+2|>3$.

Solution

The absolute value expression is already isolated. The argument $x+2$ must be less than $−3$ or greater than $3$.

$\begin{array} { c } { | x + 2 | > 3 } \\ { x + 2 < - 3 \quad \text { or } \quad x + 2 > 3 } \\ { x < - 5 }\quad\quad\quad\quad\quad\: x>1 \end{array}$

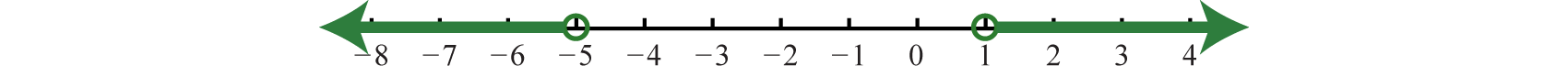
Using interval notation, $(−∞,−5)∪(1,∞)$.

Example $\PageIndex{6}$:

Solve: $13 - 2 |4x − 7| ≤ 3$.

Solution

Isolate the absolute value expression. Notice in the last step that division by $-2$ changes the inequality symbol.

$\begin{array} { r } { 13 - 2 | 4 x - 7 | \leq 3 } \\ { -2 | 4 x - 7 | \leq -10 } \\ { | 4 x - 7 | \geq 5 } \end{array}$

Next, apply the theorem and rewrite the absolute value inequality as a compound inequality with two separate intervals and solve.

$\begin{array} 4 x - 7 \leq - 5 \quad \text { or } \quad 4 x - 7 \geq 5 \end{array}$

$\begin{array} { l } \quad\:\:{ 4 x \leq 2 } \quad\quad\quad\:\:\: 4x\geq 12\\
\quad\:\:{ x \leq \frac { 2 } { 4 } } \quad\quad\quad\quad x\geq \frac { 12 } { 4 } \\
\quad\:\:{ x \leq \frac { 1 } { 2 } } \quad\quad\quad\quad x\geq 3 \end{array}$

Shade the solutions on a number line and present the answer using interval notation.

Using interval notation, $(−∞, \tfrac { 1 } { 2 }]∪[3,∞)$

$try-it.png$ Try It $\PageIndex{6}$

Solve and graph: $3 | 6 x + 5 | - 2 > 13$.

Answer

Using interval notation, $\left( - \infty , - \frac { 5 } { 3 } \right) \cup ( 0 , \infty )$

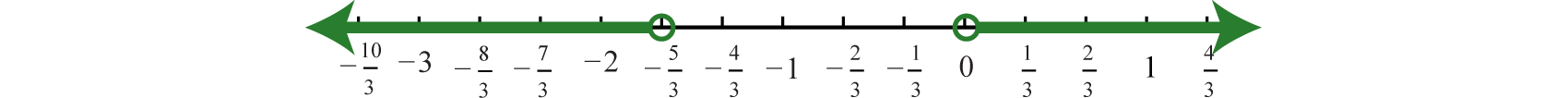
$8775b7be1a775881d4ce3e89ac626c6c.png$

Up to this point, the solution sets of linear absolute value inequalities have consisted of a single bounded interval or two unbounded intervals. This is not always the case.

Example $\PageIndex{7}$:

Solve and graph: $|2x−1|+5>2$.

Solution

Begin by isolating the absolute value.

$\begin{array} { c } { | 2 x - 1 | + 5 > 2 } \\ { | 2 x - 1 | > - 3 } \end{array}$

Notice that we have an absolute value greater than a negative number. For any real number x the absolute value of the argument will always be positive. Hence, any real number will solve this inequality.

All real numbers, $ℝ$.

Example $\PageIndex{8}$:

Solve and graph: $|x+1|+4≤3$.

Solution

Begin by isolating the absolute value.

$\begin{array} { l } { | x + 1 | + 4 \leq 3 } \\ { | x + 1 | \leq - 1 } \end{array}$

In this case, we can see that the isolated absolute value is to be less than or equal to a negative number. Again, the absolute value will always be positive; hence, we can conclude that there is no solution.

Answer: $Ø$ or $ \{ \:\: \} $