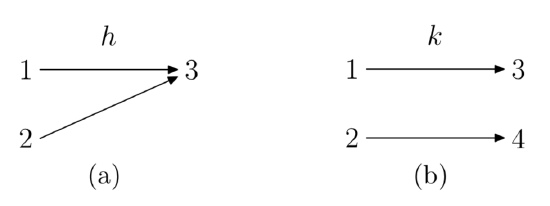2.5: One-to-One and Inverse Functions

Learning Objectives

• Understand the concept of a one-to-one function.
• Determine the conditions for when a function has an inverse.
• Use the horizontal line test to recognize when a function is one-to-one.
• Find the inverse of a given function.
• Draw the graph of an inverse function.

One-to-one functions

Some functions have a given output value that corresponds to two or more input values. For example, on a menu there might be five different items that all cost $7.99.  If the domain of a function is all of the items listed on the menu and the range is the prices of the items, then there are five different input values that all result in the same output value of $7.99.

Example \(\PageIndex{1}\): Determining Whether a Relationship Is a One-to-One Function

Is the area of a circle a function of its radius? If yes, is the function one-to-one?

Solution

A circle of radius \(r\) has a unique area measure given by \(A={\pi}r^2\), so for any input, \(r\), there is only one output, \(A\). The area is a function of radius\(r\).

If the function is one-to-one, every output value for the area, must correspond to a unique input value, the radius.

• For any given radius, only one value for the area is possible. Any area measure \(A\) is given by the formula \(A={\pi}r^2\).
• For any given area, only one value for the radius can be produced. It is not possible that a circle with a different radius would have the same area.  Any radius measure \(r\) is given by the formula \(r= \pm \sqrt{\frac{A}{\pi}}\). Because areas and radii are positive numbers, there is exactly one solution: \(\sqrt{\frac{A}{\pi}}\).

Every radius corresponds to just one area and every area is associated with just one radius.
So the area of a circle is a one-to-one function of the circle’s radius.

 Try It \(\PageIndex{1}\)

At a bank, a printout is made at the end of the day, listing each bank account number and its balance.

a. Is the ending balance a function of the bank account number?
b. Is the ending balance a one-to-one function of the bank account number?

Answer

a. yes, because each bank account has a single balance at any given time;
b. no, because each bank account corresponds to just one balance, but each balance does not correspond to just one bank account (the same balance can belong to two different accounts)..

 

Definition: One-to-One Functions

A one-to-one function is a particular type of function in which for each output value \(y\) there is exactly one input value \(x\) that is associated with it. In other words, a function is one-to-one if each output \(y\) corresponds to precisely one input \(x\).

It’s easiest to understand this definition by looking at mapping diagrams and graphs of some example functions.

Example \(\PageIndex{2}\): Definition of 1-1 functions 

Consider the two functions \(h\) and \(k\) defined according to the mapping diagrams in Figure 1. In Figure 1(a), there are two values in the domain that are both mapped onto 3 in the range. Hence, the function \(h\) is not one-to-one. On the other hand, in Figure 1(b), for each output in the range of \(k\), there is only one input in the domain that gets mapped onto it. Therefore, \(k\) is a one-to-one function.

Figure 2. Mapping diagrams help to determine if a function is one-to-one.

Identifying 1-1 functions graphically

When examining a graph of a function, if a horizontal line (which represents a single value for \(y\)), intersects the graph of a function in more than one place, then for each point of intersection, you have a different value of \(x\) associated with the same value of \(y\). Thus the \(y\) value does NOT correspond to just precisely one input, and the graph is NOT that of a one-to-one function. This idea is the idea behind the Horizontal Line Test.

Howto: Use the horizontal line test to determine if a given graph represents a 1-1 function.

1. Confirm the graph is a function by using the vertical line test. (a 1-1 function must be a function)
2. Inspect the graph to see if any horizontal line drawn would intersect the curve more than once.
3. If there is any such line, then the function is not one-to-one, but if every horizontal line intersects the graph in at most one point, then the function represented by the graph is one-to-one.

^[m] Example \(\PageIndex{3}\): HLT

Determine (a) whether each graph is the graph of a function and, if so, (b) whether it is one-to-one.

Figure 3

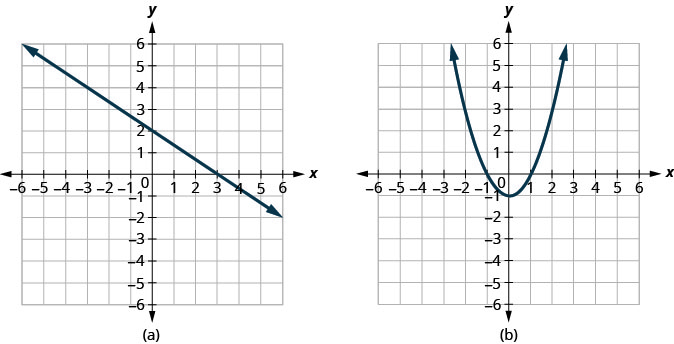
Solution:

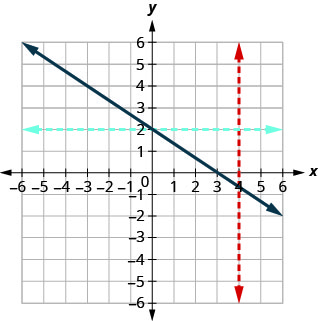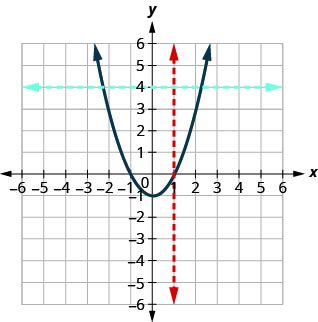Since any vertical line intersects the graph in at most one point, the graph is the graph of a function. Since any horizontal line intersects the graph in at most one point, the graph is the graph of a one-to-one function.	Since any vertical line intersects the graph in at most one point, the graph is the graph of a function. The horizontal line shown on the graph intersects it in two points. This graph does not represent a one-to-one function.

 Try It \(\PageIndex{3}\): HLT

Determine whether each graph is the graph of a function and, if so, whether it is one-to-one.

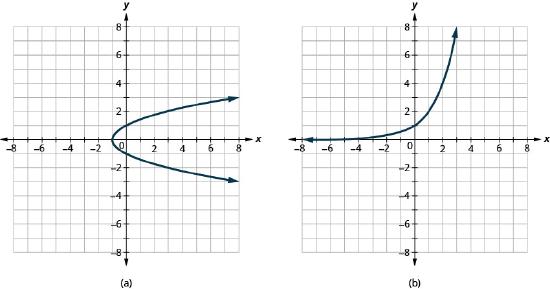
Answer

1. Not a function -- so not a one-to-one function
2. One-to-one function

Note: 1-1 function attributes

It follows from the horizontal line test that if \(f\) is a strictly increasing function, then \(f\) is one-to-one. Likewise, every strictly decreasing function is also one-to-one.

One-to-One Attribute Confirmed Algebraically

Algebraic Definition: One-to-One Functions

If a function \(f\) is one-to-one and \(a\) and \(b\) are in the domain of \(f\) then

if \( a \ne b \) then \( f(a) \ne f(b) \)	Two different \(x\) values always produce different \(y\) values
if \( f(a) = f(b) \) then \( a = b \)	No value of \(y\) corresponds to more than one value of \(x\)

Example \(\PageIndex{4}\): Confirm 1-1 algebraically

Show algebraically that \(f(x) = (x+2)^2 \) is not one-to-one

Solution

\(\begin{array}{ccc}
\qquad\text{      If } f(a) &=& f(b) \text{ then ...} \qquad\\
(a+2)^2 &=& (b+2)^2 \\
\sqrt{ (a+2)^2 } &=& \pm \sqrt{ (b+2)^2 } \\
a+2 = b+2 &or& a+2 = -(b+2) \\
a = b &or& a = -b-4 \\
\end{array}\)

Since we have shown that when \(f(a)=f(b)\) we do not always have the outcome that \(a=b\) then we can conclude the \(f\) is not one-to-one.

Implications of One-to-one Attribute when Solving Equations

One of the ramifications of being a one-to-one function \(f\) is that when solving an equation \(f(u)=f(v)\) then this equation can be solved more simply by just solving \(u = v\). This is commonly done when  log or exponential equations must be solved. Another implication of this property we have already seen when we encounter extraneous roots when square root equations are solved by squaring. This is because the solutions to \(g(x) = x^2\) are not necessarily the solutions to \( f(x) = \sqrt{x} \) because \(g\) is not a one-to-one function.

One-to-One Functions and Inverses

Let’s look at a one-to one function, \(f\), represented by the ordered pairs \(\{(0,5),(1,6),(2,7),(3,8)\}\). For each \(x\)-value, \(f\) adds \(5\) to get the \(y\)-value. To ‘undo’ the addition of \(5\), we subtract \(5\) from each \(y\)-value and get back to the original \(x\)-value. We can call this “taking the inverse of \(f\)” and name the function \(f^{−1}\).

WARNING: Notation

\(f^{−1}\) does not mean \(\dfrac{1}{f}\)

The −1 exponent is just notation in this context. When applied to a function, it stands for the inverse of the function, not the reciprocal of the function.

Figure 5

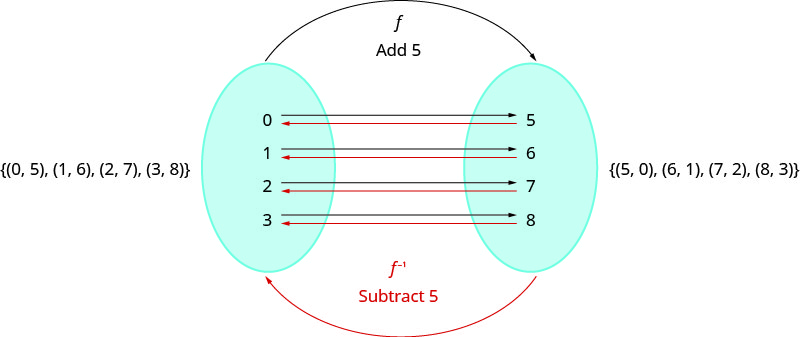
Note: One-to-one functions and Inverses

A function must be one-to-one in order to have an inverse.

Consider the function \(h\) illustrated in Figure 2(a). \(h\) is not one-to-one. If we reverse the arrows in the mapping diagram for a non one-to-one function like \(h\) in Figure 2(a), then the resulting relation will not be a function, because 3 would map to both 1 and 2. In contrast, if we reverse the arrows for a one-to-one function like \(k\) in Figure 2(b) or \(f\) in the example above, then the resulting relation IS a function which undoes the effect of the original function. Thus in order for a function to have an inverse, it must be a one-to-one function and conversely, every one-to-one function has an inverse function. 

Inverse Functions

Verification of inverse functions

When we began our discussion of an inverse function, we talked about how the inverse function ‘undoes’ what the original function did to a value in its domain in order to get back to the original \(x\)-value. This is shown diagrammatically below.

Figure 6

Putting these concepts into an algebraic form, we come up with the definition of an inverse function

Definition: Inverse Functions

\(f^{-1}(f(x))=x\), for all \(x\) in the domain of \(f\)

\(f\left(f^{-1}(x)\right)=x\), for all \(x\) in the domain of \(f^{-1}\)

We can use this property to verify that two functions are inverses of each other.

Example \(\PageIndex{6}\): Verify Inverses of linear functions

Verify that \(f(x)=5x−1\) and \(g(x)=\dfrac{x+1}{5}\) are inverse functions.

Solution:

The functions are inverses of each other if \(g(f(x))=x\) and \(f(g(x))=x\).

	\( g(f(x) ) \stackrel{?}{=} x \)		\( f(g(x) ) \stackrel{?}{=} x \)
Substitute \(5x-1\) for \(f(x)\).	\( g(5x-1 ) \stackrel{?}{=} x \)	Substitute \(\dfrac{x+1}{5}\) for \(g(x)\).	\( f \left( \dfrac{x+1}{5} \right) \stackrel{?}{=} x \)
Find \(g( {\color{Red}{5x-1}} ) \) where \(g( {\color{Red}{x}} ) = \dfrac{ {\color{Red}{x}}+1}{5} \)	\( \dfrac{( {\color{Red}{5x-1}})+1}{5}   \stackrel{?}{=} x  \)	Find \(f( {\color{Red}{\dfrac{x+1}{5}}} ) \) where \(f( {\color{Red}{x}} ) =5 {\color{Red}{x}}-1 \)	\( 5 \left( \dfrac{x+1}{5} \right) -1 \stackrel{?}{=} x \)
Simplify.	\( \dfrac{5x}{5} \stackrel{?}{=} x \) \( x=x \color{Cerulean}{✓}\)	Simplify.	\( x+1-1  \stackrel{?}{=} x  \) \( x=x \color{Cerulean}{✓}\)

Since both \(g(f(x))=x\) and \(f(g(x))=x\) are true, the functions \(f(x)=5x−1\) and \(g(x)=\dfrac{x+1}{5}\) are inverse functions of each other.

 Try It \(\PageIndex{6a}\) 

1. Verify that the functions are inverse functions. \(f(x)=4 x-3\) and \(g(x)=\dfrac{x+3}{4}\).
2. Verify that the functions are inverse functions. \(f(x)=2 x+6\) and \(g(x)=\dfrac{x-6}{2}\)

Answer

1.   \(g(f(x))=x\), and \(f(g(x))=x\), so they are inverses.
2.   \(g(f(x))=x,\) and \(f(g(x))=x,\) so they are inverses.

 Try It \(\PageIndex{6b}\) 

Show that \(f(x)=\dfrac{x+5}{3}\) and \(f^{−1}(x)=3x−5\) are inverses.

Answer

1.   \(f^{−1}(f(x))=f^{−1}(\dfrac{x+5}{3})=3(\dfrac{x+5}{3})−5=(x−5)+5=x\)
2.   \(f(f^{−1}(x))=f(3x−5)=\dfrac{(3x−5)+5}{3}=\dfrac{3x}{3}=x\)

 Notice the inverse operations are in reverse order of the operations from the original function.

Example \(\PageIndex{7}\): Verify Inverses of Rational Functions

Show that \(f(x)=\dfrac{1}{x+1}\) and \(f^{−1}(x)=\dfrac{1}{x}−1\) are inverses, for \(x≠0,−1\).

Solution

We must show that \(f^{−1}(f(x))=x\) for all \(x\) in the domain of \(f\)

\[ \begin{align*} f^{−1}(f(x)) &=f^{−1}\left(\dfrac{1}{x+1}\right)\\[4pt] &=\dfrac{1}{\dfrac{1}{x+1}}−1\\[4pt] &=(x+1)−1\\[4pt] &=x &&\text{for all } x \ne −1 \text{,  the domain of }f \end{align*}\]

and \(f(f^{−1}(x))=x\) for all \(x\) in the domain of \(f^{−1}\).

\[ \begin{align*} f(f^{−1}(x)) &=f(\dfrac{1}{x−1})\\[4pt] &=\dfrac{1}{\left(\dfrac{1}{x−1}\right)+1}\\[4pt] &=\dfrac{1}{\dfrac{1}{x}}\\[4pt] &=x &&\text{for all } x \ne 0 \text{,  the domain of }f^{−1} \end{align*}\]

Therefore, \(f(x)=\dfrac{1}{x+1}\) and \(f^{−1}(x)=\dfrac{1}{x}−1\) are inverses.

Example \(\PageIndex{8}\): Verify Inverses for Power Functions

If \(f(x)=x^3\) (the cube function) and \(g(x)=\frac{1}{3}x\), is \(g=f^{-1}\)?

Solution

\(f(g(x))=\dfrac{x^3}{27}{\neq}x\)

No, the functions are not inverses. The correct inverse to the cube is, of course, the cube root \(\sqrt[3]{x}=x^{\frac{1}{3}}\), that is, the one-third is an exponent, not a multiplier.

 Try It \(\PageIndex{8}\) 

1. If \(f(x)=x^3−4\) and \(g(x)=\sqrt[3]{x+4}\), is \(g=f^{-1}\)?
2. If \(f(x)=(x−1)^3\) and \(g(x)=\sqrt[3]{x}+1\), is \(g=f^{-1}\)?

Answer

1.  yes          2.  yes

Inverses of Ordered Pairs

Definition: Inverse of a Function Defined by Ordered Pairs.

If \(f(x)\) is a one-to-one function whose ordered pairs are of the form \((x,y)\), then its inverse function \(f^{−1}(x)\) is the set of ordered pairs \((y,x)\).

In the next example we will find the inverse of a function defined by ordered pairs.

Example \(\PageIndex{9}\): Inverse of Ordered Pairs 

Find the inverse of the function \(\{(0,3),(1,5),(2,7),(3,9)\}\). Determine the domain and range of the inverse function.

Solution:

This function is one-to-one since every \(x\)-value is paired with exactly one \(y\)-value.

To find the inverse we reverse the \(x\)-values and \(y\)-values in the ordered pairs of the function.

\(\begin{array}{ll} {\text{Function}}&{\{(0,3),(1,5),(2,7),(3,9)\}} \\ {\text{Inverse Function}}& {\{(3,0), (5,1), (7,2), (9,3)\}} \\ {\text{Domain of Inverse Function}}&{\{3, 5, 7, 9\}} \\ {\text{Range of Inverse Function}}&{\{0, 1, 2, 3\}} \end{array}\)

 Try It \(\PageIndex{9}\)

1. Find the inverse of \(\{(0,4),(1,7),(2,10),(3,13)\}\). Determine the domain and range of the inverse function.
2. Find the inverse of \(\{(-1,4),(-2,1),(-3,0),(-4,2)\}\). Determine the domain and range of the inverse function.

Answer

1. Inverse function: \(\{(4,0),(7,1),(10,2),(13,3)\}\). Domain: \(\{4,7,10,13\}\). Range: \(\{0,1,2,3\}\).
2. Inverse function: \(\{(4,-1),(1,-2),(0,-3),(2,-4)\}\). Domain: \(\{0,1,2,4\}\). Range: \(\{-4,-3,-2,-1\}\).

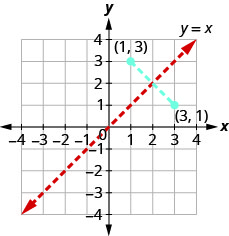Inverses from Graphs

Since every point on the graph of a function \(f(x)\) is a mirror image of a point on the graph of \(f^{−1}(x)\), we say the graphs are mirror images of each other through the line \(y=x\). We will use this concept to graph the inverse of a function in the next example.

Graph an Inverse 

We just noted that if \(f(x)\) is a one-to-one function whose ordered pairs are of the form \((x,y)\), then its inverse function \(f^{−1}(x)\) is the set of ordered pairs \((y,x)\).

So if a point \((a,b)\) is on the graph of a function \(f(x)\), then the ordered pair \((b,a)\) is on the graph of \(f^{−1}(x)\). The Figure on the right illustrates this.

The distance between any two pairs \((a,b)\) and \((b,a)\) is cut in half by the line \(y=x\). So we say the points are mirror images of each other through the line \(y=x\).

Example \(\PageIndex{10a}\): Graph Inverses

Given the graph of \(f(x)\) in Figure \(\PageIndex{10a}\), sketch a graph of \(f^{-1}(x)\).

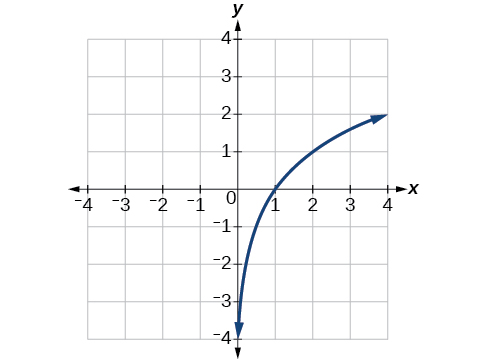
Figure \(\PageIndex{10a}\)

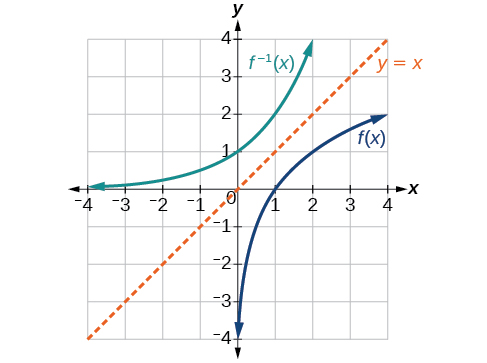Solution.  The graph of \(f(x)\) is a one-to-one function, so we will be able to sketch an inverse. Note that the graph shown has an apparent domain of \((0,\infty)\) and range of \((−\infty,\infty)\), so the inverse will have a domain of \((−\infty,\infty)\) and range of \((0,\infty)\).

If we reflect this graph over the line \(y=x\), the point \((1,0)\) reflects to \((0,1)\) and the point \((4,2)\) reflects to \((2,4)\). Sketching the inverse on the same axes as the original graph gives the graph illustrated in the Figure to the right. The graph clearly shows the graphs of the two functions are reflections of each other across the identity line \(y=x\).

Example \(\PageIndex{10b}\): Graph Inverses

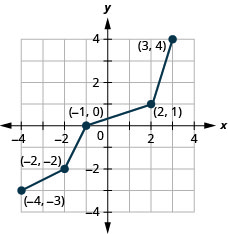
Graph, on the same coordinate system, the inverse of the one-to one function shown.

Figure 10b

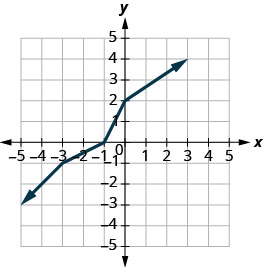
Solution:

We can use points on the graph to find points on the inverse graph. Some points on the graph are: \((−5,−3),(−3,−1),(−1,0),(0,2),(3,4)\).

So, the inverse function will contain the points: \((−3,−5),(−1,−3),(0,−1),(2,0),(4,3)\).

Graph of function ilustrated in Figure 10b and its inverse

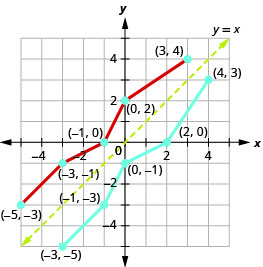
Notice how the graph of the original function and the graph of the inverse functions are mirror images through the line \(y=x\).

 Try It \(\PageIndex{10}\)

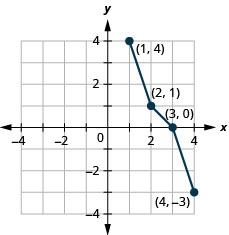
Graph, on the same coordinate system, the inverse of the one-to one function.

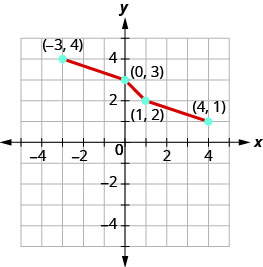Answer

Obtain Function Values for an Inverse  

Howto: Given the graph of a function, evaluate its inverse at specific points.

1. Find the desired \(x\) coordinate of \(f^{-1}\) on the \(y\)-axis of the given graph of \(f\).
2. Read the corresponding \(y\) coordinate of \(f^{-1}\) from the \(x\)-axis of the given graph of \(f\).

Example \(\PageIndex{12}\): Evaluating a Function and Its Inverse from a Graph at Specific Points

A function \(g(x)\) is given in Figure \(\PageIndex{12}\).  Find \(g(3)\) and \(g^{-1}(3)\).

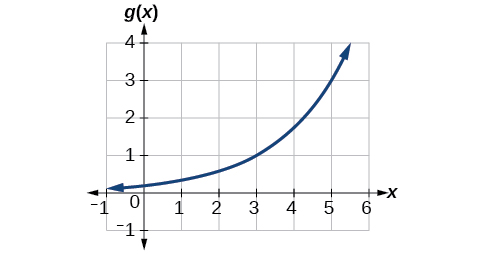
Figure \(\PageIndex{12}\): Graph of \(g(x)\)

Solution. To evaluate \(g(3)\), we find 3 on the x-axis and find the corresponding output value on the y-axis. The point \((3,1)\) tells us that \(g(3)=1\).

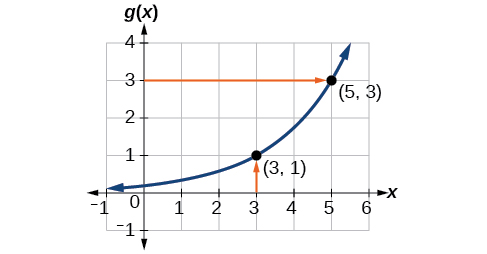
To evaluate \(g^{-1}(3)\), recall that by definition \(g^{-1}(3)\) means the value of \(x\) for which \(g(x)=3\). By looking for the output value 3 on the vertical axis, we find the point \((5,3)\) on the graph, which means \(g(5)=3\), so by definition, \(g^{-1}(3)=5.\) See Figure \(\PageIndex{12s}\) below.

Figure \(\PageIndex{12s}\): Graph of \(g(x)\).

 Try It \(\PageIndex{12}\)

Using the graph in Figure \(\PageIndex{12}\), (a) find \(g^{-1}(1)\), and (b) estimate \(g^{-1}(4)\).

Answer

(a)     3 \( \qquad \) (b)     5.6

Inverses from Equations

We have found inverses of function defined by ordered pairs and from a graph. We will now look at how to find an inverse using an algebraic equation. The method uses the idea that if \(f(x)\) is a one-to-one function with ordered pairs \((x,y)\), then its inverse function \(f^{−1}(x)\) is the set of ordered pairs \((y,x)\).

If we reverse the \(x\) and \(y\) in the function and then solve for \(y\), we get our inverse function.

We summarize the steps below.

Howto: Find the Inverse of a One-to-One Function.

Make sure that \(f\) is one-to-one. If \(f\) is not one-to-one it does NOT have an inverse. (Alternatively, the proposed inverse could be found and then it would be necessary to confirm the two are functions and indeed inverses).

1. Substitute \(y\) for \(f(x)\).
2. Interchange the variables \(x\) and \(y\).
3. Solve for \(y\).
4. Substitute \(f^{−1}(x)\) for \(y\).

Inverses of Linear Functions

Example \(\PageIndex{13}\): Inverses of a Linear Function

Find the inverse of \(f(x)=4 x+7\).

Solution:

The graph of function \(f\) is a line and so it is one-to-one.

\(\quad\) Step 1. Substitute \(y\) for \(f(x)\).	Replace \(f(x)\) with \(y\).	\(\begin{aligned} f(x) &=4 x+7 \\ y &=4 x+7 \end{aligned}\)
\(\quad\) Step 2: Interchange the variables \(x\) and \(y\).	Replace \(x\) with \(y\) and then \(y\) with \(x\).	\(x=4y+7\)
\(\quad\) Step 3: Solve for \(y\).	Subtract \(7\) from each side.  Divide by \(4\).	\(x-7=4 y\) \(\dfrac{x-7}{4}=y\)
\(\quad\) Step 4: Substitute \(f^{-1}(x)\) for \(y\).	Replace \(y\) with \(f^{-1}(x)\).	\(\dfrac{x-7}{4}=f^{-1}(x)\)

 Try It \(\PageIndex{13}\) 

1. Find the inverse of the function \(f(x)=5x-3\).
2. Find the inverse of the function \(f(x)=8 x+5\).

Answer

1.  \(f^{-1}(x)=\dfrac{x+3}{5}\)             2.   \(f^{-1}(x)=\dfrac{x-5}{8}\)

Inverses of Odd Power Functions

Example \(\PageIndex{14a}\)

Find the inverse of \(f(x) = 2x^5+3\).

Solution. A check of the graph shows that \(f\) is one-to-one (this is left for the reader to verify).

STEP 1: Write the formula in \(xy\)-equation form: \(y = 2x^5+3\).

STEP 2: Interchange \(x\) and \(y\): \(x = 2y^5+3\).

STEP 3: Solve for \(y\):

\(x = 2y^5+3\).

\(\rightarrow x−3 = 2y^5\)

\(\rightarrow \dfrac{x−3}{2} = y^5\)

\(\rightarrow \sqrt[5]{\dfrac{x−3}{2}} = y\)

STEP 4: Thus, \(f^{−1}(x) = \sqrt[5]{\dfrac{x−3}{2}}\)

Example \(\PageIndex{14b}\): Finding the Inverse of a Cubic Function

Find the inverse of the function \(f(x)=5x^3+1\).

Solution

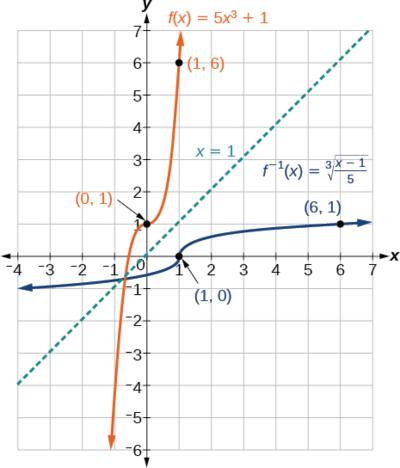This is a transformation of the basic cubic toolkit function, and based on our knowledge of that function, we know it is one-to-one. Solve for the inverse by switching \(x\) and \(y\) and solving for \(y\).

\(y=5x^3+1\)

\(x=5y^3+1\)

\(x−1=5y^3\)

\(\dfrac{x−1}{5}=y^3\)

\(f^{−1}(x)=\sqrt[3]{\dfrac{x−1}{5}}\)

Analysis

Look at the graph of \(f\) and \(f^{–1}\). Notice that one graph is the reflection of the other about the line \(y=x\). This is always the case when graphing a function and its inverse function.

Also, since the method involved interchanging \(x\) and \(y\), notice corresponding points in the accompanying figure. If \((a,b)\) is on the graph of \(f\), then \((b,a)\) is on the graph of \(f^{–1}\). Since \((0,1)\) is on the graph of \(f\), then \((1,0)\) is on the graph of \(f^{–1}\). Similarly, since \((1,6)\) is on the graph of \(f\), then \((6,1)\) is on the graph of \(f^{–1}\) .

 Try It \(\PageIndex{14}\) 

Find the inverse function of \(f(x)=\sqrt[3]{x+4}\).

Answer

\(f^{−1}(x)=x^3−4\)

Domain and Range of Inverse Functions

Notice that that the ordered pairs of \(f\) and \(f^{−1}\) have their \(x\)-values and \(y\)-values reversed. Therefore we can indirectly determine the domain and range of a function and its inverse.

Note: Domain and Range of \(f\) and \(f^{-1}\)

The domain of \(f\) is the range of \(f^{−1}\) and the domain of \(f^{−1}\) is the range of \(f\).

How To: Given a function, find the domain and range of its inverse.

1. If the function is one-to-one, write the range of the original function as the domain of the inverse, and write the domain of the original function as the range of the inverse.
2. If the domain of the original function needs to be restricted to make it one-to-one, then this restricted domain becomes the range of the inverse function.

Inverses of Radical Functions

Example \(\PageIndex{15}\): Inverse of radical functions 

Find the inverse of \(f(x)=\sqrt[5]{2 x-3}\). State the domain and range of both the function and its inverse function.

Solution:

\(f(x)=\sqrt[5]{2 x-3}\)

Substitute \(y\) for \(f(x)\). (Notice here that the domain of \(f\) is all real numbers.)

\(y=\sqrt[5]{2 x-3}\)

Interchange the variables \(x\) and \(y\).

\(x=\sqrt[5]{2 y-3}\)

Solve for \(y\).

\(\begin{aligned}(x)^{5} &=(\sqrt[5]{2 y-3})^{5} \\ x^{5} &=2 y-3 \\ x^{5}+3 &=2 y \\ \frac{x^{5}+3}{2} &=y \end{aligned}\)

Substitute \(f^{-1}(x)\) for \(y\).

\(f^{-1}(x)=\dfrac{x^{5}+3}{2}\)

Verify that the functions are inverses.

\(\begin{array}{cc} {f^{-1}(f(x)) \stackrel{?}{=} x} & {f\left(f^{-1}(x)\right) \stackrel{?}{=} x} \\
{f^{-1}(\sqrt[5]{2x-3})  \stackrel{?}{=}x}  &{f\left(\frac{x^{5}+3}{2} \right)}\stackrel{?}{=}x \\
{\dfrac{(\sqrt[5]{2x-3})^{5}+3}{2}  \stackrel{?}{=}x}  &{\sqrt[5]{2\left(\dfrac{x^{5}+3}{2} \right)-3}\stackrel{?}{=}x} \\
{\dfrac{2x-3+3}{2}  \stackrel{?}{=}x}  &{\sqrt[5]{x^{5}+3-3}\stackrel{?}{=}x}\\
{\dfrac{2x}{2}  \stackrel{?}{=}x}  &{\sqrt[5]{x^{5}}\stackrel{?}{=}x} \\
{x=x}&{x=x} \end{array}\)

Domain and Range.	\(f(x)=\sqrt[5]{2 x-3}\)	Domain of \(f\): \( ( -\infty, \infty)\)	Range of \(f\):  \( ( -\infty, \infty)\)
	\(f^{−1}(x)=\dfrac{x^{5}+3}{2}\)	Domain of \(f^{-1}\):  \( ( -\infty, \infty)\)	Range of \(f^{-1}\): \( ( -\infty, \infty)\)

 Try It \(\PageIndex{15}\)

1. Find the inverse of the function \(f(x)=\sqrt[5]{3 x-2}\).
2. Find the inverse of the function \(f(x)=\sqrt[4]{6 x-7}\). State the domain and range of \(f\) and its inverse.

Answer

1. \(f^{-1}(x)=\dfrac{x^{5}+2}{3}\)
2. \(f^{-1}(x)=\dfrac{x^{4}+7}{6}\)

\(\;  f(x)=\sqrt[4]{6 x-7}\)	Domain of \(f\): \( \big[ \frac{7}{6}, \infty)\)	Range of \(f\):  \( ( -\infty, \infty)\)
\(\;  f^{−1}(x)=\dfrac{x^4+7}{6}  \)	Domain of \(f^{-1}\):  \( ( -\infty, \infty)\)	Range of \(f^{-1}\): \( \big[  \frac{7}{6}, \infty)  \)

If we want to find the inverse of a radical function, we will need to restrict the domain of the answer if the range of the original function is limited.

Example \(\PageIndex{16}\): Solving to Find an Inverse with Square Roots

Find the inverse of the function \(f(x)=2+\sqrt{x−4}\).

Solution

\[ \begin{align*} y&=2+\sqrt{x-4} \\
x&=2+\sqrt{y-4} \\
x-2 &=\sqrt{y-4} &\text{Before squaring, } x -2 \ge 0 \text{ so } x \ge 2 \\
(x-2)^2&=y-4 \\
y&=(x-2)^2+4 \end{align*}\]

So \(f^{-1}(x)=(x−2)^2+4\), \(x \ge 2\). Since the domain restriction \(x \ge 2\) is not apparent from the formula, it should always be specified in the function definition.

The domain of \(f\) is \(\left[4,\infty\right)\) so the range of \(f^{-1}\) is also \(\left[4,\infty\right)\).
Since the domain of \(f^{-1}\) is \(x \ge 2\)  or \(\left[2,\infty\right)\), the range of \(f\) is also \(\left[2,\infty\right)\).

Analysis

The formula we found for \(f^{-1}(x)=(x-2)^2+4\) looks like it would be valid for all real \(x\). However, BOTH \(f^{-1}\)  and \(f\) must be one-to-one functions and \(y=(x-2)^2+4\) is a parabola which clearly is not one-to-one. This is where the subtlety of the restriction to \(x\) comes in during the solving for \(y\). Recall that squaring can introduce extraneous solutions and that is precisely what happened here - after squaring, \(x\) had no apparent  restrictions, but before squaring, \(x-2\) could not be negative. Thus, \(x \ge 2\) defines the domain of \(f^{-1}\). Also observe this domain of \(f^{-1}\) is exactly the range of \(f\).

 Try It \(\PageIndex{16}\) 

What is the inverse of the function \(f(x)=2-\sqrt{x}\)? State the domains of both the function and the inverse function.

Answer

\(f^{-1}(x)=(2−x)^2\), \(x \le 2\); domain of \(f\): \(\left[0,\infty\right)\); domain of \(f^{-1}\): \(\left(−\infty,2\right]\)

 Try It \(\PageIndex{17}\) 

What is the inverse of the function  \(f(x)=\sqrt{2x+3}\)? State the domain and range of both the function and the inverse function.

Answer

\(f(x)=\sqrt{2x+3}\)	Domain of \(f\): \(\left[ -\tfrac{3}{2},\infty \right)\)	Range of \(f\):  \(\left[0,\infty\right)\)
\(f^{−1}(x)=\dfrac{x^2−3}{2}\), \(x≥0\)	Domain of \(f^{-1}\):  \(\left[0,\infty\right)\)	Range of \(f^{-1}\): \(\left[ -\tfrac{3}{2},\infty \right)\)

Inverses of Rational Functions

Example \(\PageIndex{18}\)

Find the inverse of \(f(x) = \dfrac{5}{7+x}\).

Solution

A check of the graph shows that \(f\) is one-to-one (this is left for the reader to verify).

STEP 1: Write the formula in \(xy\)-equation form: \(y = \dfrac{5}{7+x}\).

STEP 2: Interchange \(x\) and \(y:\) \(x = \dfrac{5}{7+y}\).

STEP 3: Solve for \(y:\)

\(x = \dfrac{5}{7+y}\)

\(\rightarrow x(7+y) = 5\)

\(\rightarrow 7+y = \dfrac{5}{x}\)

\(y = \dfrac{5}{x}−7 = \dfrac{5 − 7x}{x}\)

STEP 4: Thus, \(f^{−1}(x) = \dfrac{5 − 7x}{x}\)

Example \(\PageIndex{19}\): Solving to Find an Inverse Function

Find the inverse of the function \(f(x)=\dfrac{2}{x−3}+4\).

Solution

\[\begin{align*} y&=\dfrac{2}{x−3+4} &&\text{Set up an equation.} \\
x&=\dfrac{2}{y−3+4} &&\text{Switch variables.} \\
x−4&=\dfrac{2}{y−3} &&\text{Subtract 4 from both sides.} \\
y−3&=\dfrac{2}{x−4} &&\text{Multiply both sides by } y−3 \text{ and divide by } x−4. \\
y&=\dfrac{2}{x−4}+3 &&\text{Add 3 to both sides.} \end{align*}\]

So \(f^{-1}(x)=\dfrac{2}{x−4}+3\).

\(f(x)=\dfrac{2}{x−3}+4\)	Domain of \(f\): \( ( -\infty, 3] \cup [3,\infty)\)	Range of \(f\):  \( ( -\infty, 4] \cup [4,\infty)\)
\(f^{-1}(x)=\dfrac{2}{x−4}+3\)	Range of \(f^{-1}\): \( ( -\infty, 4] \cup [4,\infty)\)	Domain of \(f^{-1}\): \( ( -\infty, 3] \cup [3,\infty)\)

Example \(\PageIndex{20}\)

This example is a bit more complicated: find the inverse of the function \(f(x) = \dfrac{5x+2}{x−3}\).

Solution

A check of the graph shows that \(f\) is one-to-one (this is left for the reader to verify).

STEP 1: Write the formula in xy-equation form: \(y = \dfrac{5x+2}{x−3}\).

STEP 2: Interchange \)x\) and \(y:\) \(x = \dfrac{5y+2}{y−3}\).

STEP 3: Solve for \(y:\)

\(x = \frac{5y+2}{y−3}\)

\(\rightarrow x(y−3) = 5y+2\)

\(\rightarrow xy−3x = 5y+2\)

This equation is linear in \(y.\) Isolate the terms containing the variable \(y\) on one side of the equation, factor, then divide by the coefficient of \(y.\)

\(xy−3x = 5y+2\)

\(xy−5y = 3x+2\)

\(y(x−5) = 3x+2\)

\(y = \dfrac{3x+2}{x−5}\)

STEP 4: Thus, \(f^{−1}(x) = \dfrac{3x+2}{x−5}\).

Inverse of a domain restricted quadratic

Example \(\PageIndex{21}\)

Find the inverse function for \(h(x) = x^2\)

Solution

According to the horizontal line test, the function \(h(x) = x^2\) is certainly not one-to-one. However, if we only consider the right half or left half of the function, by restricting the domain to either the interval \([0, \infty)\) or \((−\infty,0],\) then the function is one-to-one, and therefore would have an inverse.

We will choose to restrict the domain of \(h\) to the left half of the parabola as illustrated in Figure 21(a) and find the inverse for the function \(f(x) = x^2\), \(x \le 0\). In this case, the procedure still works, provided that we carry along the domain condition in all of the steps.

The graph in Figure 21(a) passes the horizontal line test, so the function \(f(x) = x^2\), \(x \le 0\), for which we are seeking an inverse, is one-to-one.

Step 1: Write the formula in \(xy\)-equation form: \(y = x^2\), \(x \le 0\)

Step 2: Interchange \(x\) and \(y\): \(x = y^2\), \(y \le 0\). Note how \(x\) and \(y\) must also be interchanged in the domain condition.

Step 3: Solve for \(y\): \(y = \pm \sqrt{x}\), \(y \le 0\)

Now there are two choices for \(y\), one positive and one negative, but the condition \(y \le 0\) tells us that the negative choice is the correct one. Thus, the last statement is equivalent to \(y = −\sqrt{x}\).

Step 4: Thus, \(f^{−1}(x) = −\sqrt{x}\). The graph of \(f^{−1}\) is shown in Figure 21(b), and the graphs of both f and \(f^{−1}\) are shown in Figure 21(c) as reflections across the line y = x.

Figure 21. Domain of a Quadratic is Restricted to a part that is 1-1 before an inverse can be found.
Inverse functions are reflections across the line \(y=x\).

Example \(\PageIndex{22}\): Restricting the Domain to Find the Inverse of a Polynomial Function

Find the inverse function of \(f\):

1. \(f(x)={(x−4)}^2\), \(x≥4\)
2. \(f(x)={(x−4)}^2\), \(x≤4\)

Solution

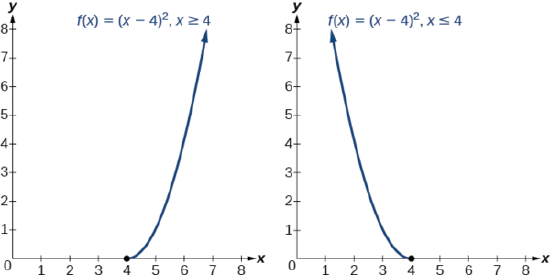The original function \(f(x)={(x−4)}^2\) is not one-to-one, but the function can be restricted to a domain of \(x≥4\) or \(x≤4\) on which it is one-to-one (These two possibilities are illustrated in the figure to the right.) To find the inverse, start by replacing \(f(x)\) with the simple variable \(y\). (We will choose which domain restriction is being used at the end).

\(y={(x−4)}^2\) Interchange \(x\) and \(y\).

\(x={(y−4)}^2\) Take the square root.

\(\pm \sqrt{x}=y−4\) Add \(4\) to both sides.

\(4\pm \sqrt{x} =y\) so \( y = \begin{cases} 4+ \sqrt{x} & \longrightarrow y \ge 4\\ 4 - \sqrt{x} & \longrightarrow y \le 4 \end{cases}\)

This expression for \(y\) is not a function. We need to go back and consider the domain of the original domain-restricted function we were given in order to determine the appropriate choice for \(y\) and thus for \(f^{−1}\).

1. Given the function \(f(x)={(x−4)}^2\), \(x≥4\), the domain of \(f\) is restricted to \(x≥4\), so the range of \(f^{−1}\) needs to be the same. Therefore, \(y≥4\), and we must use the + case for the inverse:

   \(f^{−1}(x)=4+\sqrt{x}\)

2. Given the function \(f(x)={(x−4)}^2\), \(x≤4\), the domain of \(f\) is restricted to \(x≤4\), so the range of \(f^{−1}\) needs to be the same. Therefore, \(y≤4\), and we must use the – case for the inverse:

   \(f^{−1}(x)=4−\sqrt{x}\)

Analysis

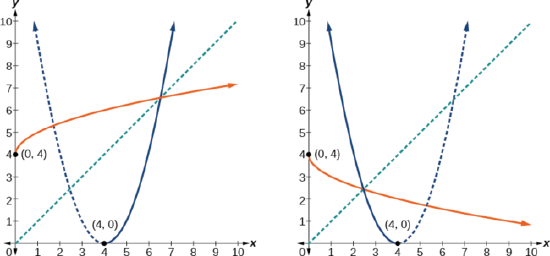On the graphs in the figure to the right, we see the original function graphed on the same set of axes as its inverse function. Notice that together the graphs show symmetry about the line \(y=x\). The coordinate pair \((4,0)\) is on the graph of \(f\) and the coordinate pair \((0, 4)\) is on the graph of \(f^{−1}\). For any coordinate pair, if \((a, b)\) is on the graph of \(f\), then \((b, a)\) is on the graph of \(f^{−1}\). Finally, observe that the graph of \(f\) intersects the graph of \(f^{−1}\) on the line \(y=x\). Points of intersection for the graphs of \(f\) and \(f^{−1}\) will always lie on the line \(y=x\).

Example \(\PageIndex{23}\): Finding the Inverse of a Quadratic Function When the Restriction Is Not Specified

Restrict the domain and then find the inverse of \(f(x)=x^2-4x+1\).

Solution

We can see this is a parabola that opens upward. Because the graph will be decreasing on one side of the vertex and increasing on the other side, we can restrict this function to a domain on which it will be one-to-one by limiting the domain to one side of the vertex. The \(x\)-coordinate of the vertex can be found from the formula \(x = \dfrac{-b}{2a} = \dfrac{-(-4)}{2 \cdot 1} = 2\). Therefore, we will choose to restrict the domain of \(f\) to \(x≥2\).

To find the inverse, we start by replacing \(f(x)\) with a simple variable, \(y\), switching \(x\) and \(y\), and then solving for \(y\). Solving for \(y\) turns out to be a bit complicated because there is both a \(y^2\) term and a \(y\) term in the equation. The approach is to use either Complete the Square or the Quadratic formula to obtain an expression for \(y\). 

\(y=x^2-4x+1\), \(x≥2\)  Interchange \(x\) and \(y\).

\(x=y^2-4y+1\),  \(y≥2\) Solve for \(y\) using Complete the Square !

\(x-1=y^2-4y\),  \(y≥2\) Isolate the \(y\) terms.

\(x-1+4=y^2-4y+4\),  \(y≥2\) Add the square of half the \(y\) coefficient.

\(x+3={(y−2)}^2\) Take the square root.

\(\pm \sqrt{x+3}=y−2\) Add 2 to both sides.

\(2\pm \sqrt{x+3}=y\) Rename the function.

\(f^{−1}(x)=2\pm \sqrt{x+3}\)

\(f^{−1}(x)= \begin{cases} 2+ \sqrt{x+3} &\ge2 \\
2-\sqrt{x+3} &\le2
\end{cases} \)

Now we need to determine which case to use. Because we restricted our original function to a domain of \(x≥2\), the outputs of the inverse are \( y≥2 \)  so we must use the + case

\(f^{−1}(x)=2+\sqrt{x+3}\)

Analysis

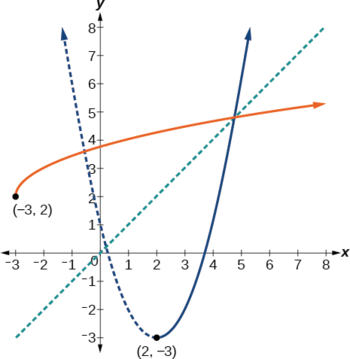Notice that we arbitrarily decided to restrict the domain on \(x≥2\). We could just as easily have opted to restrict the domain to \(x≤2\), in which case \(f^{−1}(x)=2−\sqrt{x+3}\). Observe the original function graphed on the same set of axes as its inverse function in the figure on the right. Notice that both graphs show symmetry about the line \(y=x\). The coordinate pair \((2, −3)\) is on the graph of \(f\) and the coordinate pair \((−3, 2)\) is on the graph of \(f^{−1}\). Observe from the graph of both functions on the same set of axes that

domain of \(f=\) range of \(f^{–1}=[2,\infty)\)

and

domain of \(f^{–1}=\) range of \(f=[–3,\infty)\).

Finally, observe that the graph of \(f\) intersects the graph of \(f^{−1}\) along the line \(y=x\).

 Try It \(\PageIndex{24}\) 

Find the inverse of the function \(f(x)=x^2+1\), on the domain \(x≥0\).

Answer

\(f^{−1}(x)=\sqrt{x−1}\)

 
Can more than one formula from a piecewise function be applied to a value in the domain? 

Yes. If \(f=f^{-1}\), then \(f(f(x))=x\), and we can think of several functions that have this property. The identity function does, and so does the reciprocal function, because \( 1 / (1/x) = x\). Any function \(f(x)=c−x\), where \(c\) is a constant, is also equal to its own inverse.

Key Concepts

• Horizontal Line Test: If every horizontal line, intersects the graph of a function in at most one point, it is a one-to-one function.
• Inverse of a Function Defined by Ordered Pairs: If \(f(x)\) is a one-to-one function whose ordered pairs are of the form \((x,y)\), then its inverse function \(f^{−1}(x)\) is the set of ordered pairs \((y,x)\).
• Inverse Functions: For every \(x\) in the domain of one-to-one functions \(f\) and \(f^{−1}\), \(f^{-1}(f(x))=x\) and \(f\left(f^{-1}(x)\right)=x\)
• How to Find the Inverse of a One-to-One Function:
  1. Substitute \(y\) for \(f(x)\).
  2. Interchange the variables \(x\) and \(y\).
  3. Solve for \(y\).
  4. Substitute \(f^{−1}(x)\) for \(y\).
  5. Verify that the functions are inverses.

Glossary

one-to-one function

A function is one-to-one if each value in the range has exactly one element in the domain. For each ordered pair in the function, each \(y\)-value is matched with only one \(x\)-value.