3.1: Graphs of Quadratic Functions

Graphs of Quadratic Functions

A Quadratic Function is any function defined by a polynomial whose greatest exponent is two. That means it can be written in the form \(f(x)=ax^2+bx+c\), with the restrictions that the parameters \(a\), \(b\), and \(c\) are real numbers and \(a\) canNOT be zero.  

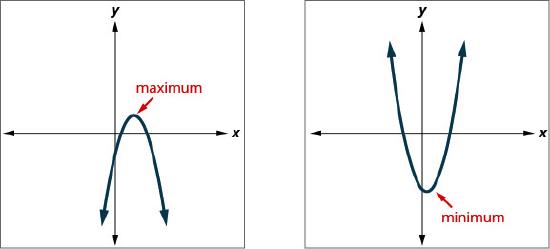
The graph of any quadratic function is a U-shaped curve called a parabola. There are certain key features that are important to recognize on a graph and to calculate from an equation.

Key features of a parabola

The orientation of a parabola is that it either opens up or opens down The vertex is the lowest or highest point on the graph The axis of symmetry is the vertical line that goes through the vertex, dividing the parabola into two equal parts. If \(h\) is the \(x\)-coordinate of the vertex, then the equation for the axis of symmetry is \(x=h\). The maximum or minimum value of a parabola is the \(y\)-coordinate of the vertex. The \(y\)-intercept is the point at which the parabola crosses the \(y\)-axis. The \(x\)-intercepts are the points at which the parabola crosses the \(x\)-axis. The domain of a parabola is all real numbers, \( (-\infty, \infty) \). The range of  a parabola starts or ends with the value of the \(y\)-coordinate of the vertex.

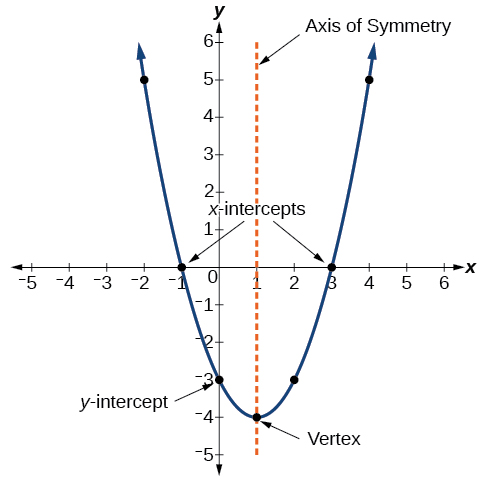
Figure \(\PageIndex{1}\): Graph illustrating features of a parabola .

Example \(\PageIndex{1}\): Identify Features of a Parabola from a graph

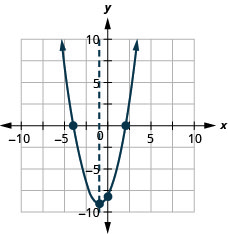
Determine features of th parabola illustrated below.

Solution. Orientation: opens up Vertex: \((3,1)\) Axis of symmetry: \(x=3\) Minimum Value: \(y=1\) \(y\)-intercept: \((0,7)\) \(x\)-intercept: none Domain: \( (-\infty, \infty) \) Range: \([1, \infty)\)

 

Forms of a Quadratic Function

There are two important forms of a quadratic function

Definitions: Forms of Quadratic Functions

A quadratic function is a polynomial function of degree two. The graph of a quadratic function is a parabola.

• The general form of a quadratic function is \(f(x)=ax^2+bx+c\) with real number parameters \(a\), \(b\), and \(c\) and \(a{\neq}0\).
• The standard form or vertex form of a quadratic function is \(f(x)=a(x−h)^2+k\) with real number parameters \(a\), \(h\), and \(k\) and \(a{\neq}0\).  NOTICE the minus sign in front of the parameter \(h\)!!

The graph of a quadratic in standard form, \(f(x)=a(x−h)^2+k\), is a graph of  \(y=x^2\) that has been shifted horizontally \(h\) units and vertically \(k\) units. Thus the vertex, originally at at \((0,0)\), is located at the point \((h, k)\) in the graph of \(f\). 

A formula for the location of the vertex for a quadratic in general form can be found by equating the two forms for a quadratic.

\[\begin{align*} a(x−h)^2+k &= ax^2+bx+c \\[4pt] ax^2−2ahx+(ah^2+k)&=ax^2+bx+c \end{align*} \]

This is an identity, so it is true for ALL values of \(x\): the coefficients for the \(x^2\) terms must be the same, the coefficients for the \(x\) terms must be the same, and the constant terms must be the same. Equating the \(x\) coefficients we get

\[–2ah=b \text{, so } h=−\dfrac{b}{2a}. \nonumber\]

This is a formula for the \(x\)-coordinate of the vertex. The \(y\)-coordinate of the vertex is \(y = f(h)=k\).

Features of the graph of a quadratic function depend on the parameter values  \(a\), \(b\), \(c\)  or \(a\), \(h\), \(k\) used in its equation. How features of the parabola for a quadratic function can be obtained is summarized below.

How to: Find Features of a Parabola Given a Quadratic Equation

• Orientation 
  • \(a > 0\), the parabola opens up \( \stackrel {+  \:\:\:    +}  {\bigcup} \)
  • \(a < 0 \), the parabola opens down \( \stackrel{- \:\:\:  -}{\bigcap } \)
• The vertex is located at \((h,k)\).  
  • If the function is in general form, calculate \(h\) and \(k\):  \(h=\dfrac{-b}{2a}, \qquad k=f(h)=f(\dfrac{−b}{2a}).\)
• The axis of symmetry, \(x=h\) is the \( \underline {\textrm{equation}} \) of the vertical line through the vertex.
• The maximum or minimum value depends on the \(y\)-coordinate, \(k\), of the vertex and the orientation of the parabola
  • If (\a > 0\), the parabola opens up and the vertex is the lowest point on the graph with a minimum value \(k\).
  • If (\a < 0\), the parabola opens down and the vertex is the highest point on the graph with a maximum value \(k\).
• The domain is always  \( \mathbb{R}\) or \( (-\infty, \infty) \).
  The range depends on the \(y\)-coordinate, \(k\), of the vertex and the orientation of the parabola
  • If \(a > 0\), the vertex is the lowest point on the graph so the range of the function is \( [k,\infty) \).
  • If \(a < 0\), the vertex is the highest point on the graph so the range of the function is \((-\infty, k] \).
• Intercepts are the points where the parabola crosses the axes.
  • The \(x\)-intercepts are the points \((s, 0)\), where \(s\) is a real solution to \(f(x)=0\)
  • The \(y\)-intercept is the point \((0, f(0))\).

Orientation

When the quadratic term, \(ax^2\), is positive, the parabola opens upward, and when the quadratic term is negative, the parabola opens downward.

Example \(\PageIndex{2}\): Find the orientation of a parabola

Determine whether each parabola opens upward or downward:

a. \(f(x)=-3 x^{2}+2 x-4\) a. Solution: \( \quad \) Find the value of \(a\). \(f(x)  =  ax^2  + bx + c\) \(f(x)=-3 x^{2}+2 x-4\) \(a=-3\) \( \quad \) Since the \(a\) is negative, the parabola will open downward.

b. \(f(x)=6 (x+1)^{2}-11\) b. Solution: \( \quad \) Find the value of \(a\). \(f(x)  =  a(x - h)^2  +  k\) \(f(x)=6(x+1)^2-11\) \(a=6\) \( \quad \) Since the \(a\) is positive, the parabola will open upward.

Try It \(\PageIndex{2}\)

Determine whether the graph of each function is a parabola that opens upward or downward:

\(f(x)=2 x^{2}+5 x-2\) \(f(x)=-3(x-4)^{2}+7\) Answer up \(\qquad\) b. down

\(f(x)=-2 x^{2}-2 x-3\) \(f(x)=5(x+1)^{2}+4\) Answer down \(\qquad\) d. up

Vertex and Axis of Symmetry

When given a quadratic in standard form \(f(x)=a(x−h)^2+k\), the vertex and axis of symmetry is easily found once the parameters \(h\) and \(k\) have been identified. (Notice the sign on \(h\)!!) The vertex is \((h, k)\) and the axis of symmetry is the vertical line \( x=h\).

When given a quadratic in general form: \(f(x)=ax^2+bx+c\), more computation is required. After identifying parameters \(a\) and \(b\), calculate \(h=–\dfrac{b}{2a}\). Then find the corresponding \(y\) coordinate for that point on the graph: \( y=f(h)=k \). Once \(h\) and \(k\) have been determined, the vertex is at \((h, k)\) and the axis of symmetry is the vertical line \( x=h\).

Example \(\PageIndex{3a}\): Find the Vertex from the General Form of the Quadratic Equation

For the graph of \(f(x)=3x^{2}-6 x+2\) find (a) the axis of symmetry and (b) the vertex.

Solution:

\( \begin{array}{llc}
\text{a.} & \text{Identify the equation parameters} & a=3, b=-6, c=2 \\
& \text{The axis of symmetry is the vertical line } x=-\frac{b}{2 a}  & \\
& \text{Substitute the values }a \text{ and } b \text{ into the formula} & x=-\frac{-6}{2 \cdot 3}=1 \\
&& \text{The axis of symmetry is the line } x=1\\
\end{array} \)

\( \begin{array}{llc}
\text{b.} & \text{The vertex is a point on the line of symmetry, so} & \text{ The } x \text{ coordinate of the vertex is } x=1\\
& \text{The }y \text{ coordinate will be }f(1) & f(1)=3({\color{red}{1}})^2-6({\color{red}{1}})+2 \\
& \text{Simplify} & f(1) = 3-6+2 \\
& \text{The result is the }y\text{ coordinate of the vertex.} & f(1)=-1 \\
&& \text{The vertex is } (1, -1)\\
\end{array} \)

Example \(\PageIndex{3b}\): Find the Vertex from the Standard Form of the Quadratic Equation

For the graph of \(f(x)=6(x-3)^{2}+4\) find:

1. the axis of symmetry
2. the vertex

Solution:

\( \begin{array}{lll}
\text{a.} & \text{Identify the equation parameters} & a=6, h=3, k=4 \\
& \text{The axis of symmetry is the vertical line } x=h & \\
& \text{Substitute.} &  \text{The axis of symmetry is the line } x=3\\
\\
\text{b.} &\text{Use the equation parameters} & a=6, h=3, k=4 \\
& \text{The vertex is the point } (h, k) &   \text{The vertex is the point } (3,4)\\
\end{array} \)

Try It \(\PageIndex{3}\)

For the following quadratic functions find a. the axis of symmetry and b. the vertex

\(f(x)=2x^{2}-8 x+1\) Answer \(x=2\) \(\qquad \) b. \((2,-7)\)

\(f(x)=2(x-1)^{2}-5\) Answer \(x=1\) \(\qquad \) b. \((1,-5)\)

Minimum or Maximum Value of a Quadratic Function

Knowing that the vertex of a parabola is the lowest or highest point of the parabola gives us an easy way to determine the minimum or maximum value of a quadratic function. The \(y\)-coordinate of the vertex of the graph of a quadratic function is the minimum value of the quadratic equation if the parabola opens upward. the maximum value of the quadratic equation if the parabola opens downward.

Example \(\PageIndex{4}\)

Find the minimum or maximum value of the quadratic function \(f(x)=x^{2}+2 x-8\).

Solution:

\( \begin{array}{llc}
 \text{Identify the equation parameters} & a=1, b=2, c=-8 \\
 \text{Since }a \text{ is positive, the parabola opens upward. }  & \text{The quadratic equation has a minimum.}  \\
 \text{State the formula for the axis of symmetry } & x=-\dfrac{b}{2 a} \\
 \text{Substitute and simplify.} & x=-\dfrac{2}{2 \cdot 1}= -1 \quad \text{The axis of symmetry is the line } x=-1\\
& \qquad \qquad \qquad \qquad \text{ The } x \text{ coordinate of the vertex is } x=-1\\
 \text{The }y \text{ coordinate will be }f(-1) & f(-1)=({\color{red}{-1}})^2-2({\color{red}{-1}})-8 \\
 \text{Simplify} & f(-1) = 1-2-8 \\
 \text{The result is the }y\text{ coordinate of the vertex.} & f(-1)=-9 \qquad \text{The vertex is } (-1, -9)\\
\end{array} \)

Since the parabola has a minimum, the \(y\)-coordinate of the vertex is the minimum \(y\)-value of the quadratic equation. The minimum value of the quadratic is \(-9\) and it occurs when \(x=-1\).

Try It \(\PageIndex{4}\)

Find the maximum or minimum value of the quadratic function

1. \(f(x)=x^{2}-8 x+12\).
2. \(f(x)=-4(x-2)^{2}+5\).

Answers

a. The minimum value of the quadratic function is \(−4\) and it occurs when \(x=4\).

b. The maximum value of the quadratic function is \(5\) and it occurs when \(x=2\).

Domain and Range

Any number can be the input value, \(x\), to a quadratic function. Therefore, the domain of any quadratic function is all real numbers. Because parabolas have a maximum or a minimum point, the range is restricted. Since the vertex of a parabola will be either a maximum or a minimum, the range will consist of all \(y\)-values greater than or equal to the \(y\)-coordinate at the vertex or less than or equal to the \(y\)-coordinate at the vertex, depending on whether the parabola opens up or down.

Given a quadratic function, find the domain and range.

1. The domain of any quadratic function is always  \( \mathbb{R}\) or \( (-\infty, \infty) \).
2. Determine the maximum or minimum value of the parabola, \(k\)
   1. If the function is in the form \(f(x)=a(x−h)^2+k\), then the value of \(k\) is readily visible as one of the parameters.
   2. If the function is in the form \(f(x)=ax^2+bx+c\), the vertex must be determined and the value for \(k\) is the \(y\) coordinate of the vertex.
3. Determine whether \(a\) is positive or negative.
   1. If \(a\) is positive, the parabola has a minimum value of \(k\) and the range of the function is \( [k,\infty) \).
   2. If \(a\) is negative, the parabola has a maximum value of \(k\) and the range of the function is \((-\infty, k] \).

Example \(\PageIndex{5}\): Find the Domain and Range of a Quadratic Function

Find the domain and range of \(f(x)=−5x^2+9x−1\).

Solution

As with any quadratic function, the domain is all real numbers.

Because \(a\) is negative, the parabola opens downward and has a maximum value.
The maximum value must be determined. Begin by finding the \(x\)-value of the vertex.

\( h=−\dfrac{b}{2a} =−\dfrac{9}{2(-5)}=\dfrac{9}{10} \)

The maximum value is given by \(f(h)\).

\(f(\frac{9}{10})=−5(\frac{9}{10})^2+9(\frac{9}{10})-1 = \frac{61}{20}\)

The range is \(f(x){\leq}\frac{61}{20}\), or \(\left(−\infty,\frac{61}{20}\right]\).

Try It \(\PageIndex{5}\)

Find the domain and range of \(f(x)=2\Big(x−\frac{4}{7}\Big)^2+\frac{8}{11}\).

Answer

The domain is all real numbers. The range is \(f(x){\geq}\frac{8}{11}\), or \(\left[\frac{8}{11},\infty\right)\).

Intercepts

The \(y\)-intercept is the point where the graph crosses the \(y\) axis. All points on the \(y\)-axis have an \(x\) coordinate of zero, so the \(y\)-intercept of a quadratic is found by evaluating the function \(f(0)\).

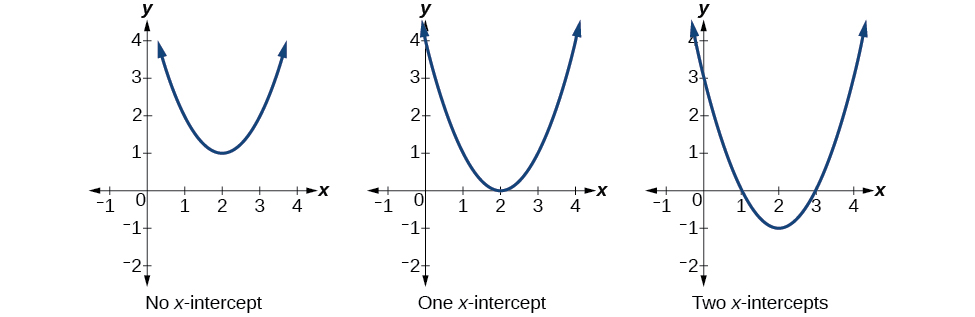
The \(x\)-intercepts are the points where the graph crosses the \(x\)-axis.  All points on the \(x\)-axis have a \(y\) coordinate of zero, so the \(x\)-intercept of a quadratic can be found by solving the equation \(f(x)=0\).  Notice in Figure \(\PageIndex{6}\) that the number of \(x\)-intercepts can vary depending upon the location of the graph.

Figure \(\PageIndex{6}\): Number of \(x\)-intercepts of a parabola.

Given a quadratic function \(f(x)\), find the \(y\)- and \(x\)-intercepts.

1. Evaluate \(f(0)\) to find the \(y\)-intercept. The \(y\) intercept is written in the form of a coordinate point \(0, f(0)\).
2. Solve the quadratic equation \(f(x)=0\) to find the \(x\)-intercepts. Each real number solution \(x_i\) is written as an \(x\)-intercept in the form \(x_i, 0\).

Example \(\PageIndex{6}\): Finding the \(y\)- and \(x\)-intercepts of a General Form Quadratic

Find the \(y\)- and \(x\)-intercepts of the quadratic \(f(x)=3x^2+5x−2\).

Solution

Find the \(y\)-intercept by evaluating \(f(0)\).

\( f(0)=3(0)^2+5(0)−2 =−2 \)

So the \(y\)-intercept is at \((0,−2)\).

For the \(x\)-intercepts, find all solutions of \(f(x)=0\).

\(0=3x^2+5x−2\)

In this case, the quadratic can be factored easily, providing the simplest method for solution. Typically, quadratics in general form, like this example, are usually solved using factoring, or failing that, using the quadratic formula or complete the square.

\(0=(3x−1)(x+2)\)

\[\begin{align*} 0&=3x−1 & 0&=x+2 \\ x&= \frac{1}{3} &\text{or} \;\;\;\;\;\;\;\; x&=−2 \end{align*}  \]

So the \(x\)-intercepts are at \((\frac{1}{3},0)\) and \((−2,0)\).

Example \(\PageIndex{7}\): 

Find the \(y\)- and \(x\)-intercepts of the quadratic \( f(x)=x^2+x+2\).

Solution

Find the \(y\)-intercept by evaluating \(f(0)\).

\( f(0)=(0)^2+(0)+2 =2 \)

So the \(y\)-intercept is at \((0, \; 2)\).

For the \(x\)-intercepts, find all solutions of \(f(x)=0\) or  \( x^2+x+2 = 0\). Clearly this does not factor, so employ the quadratic formula. 

The quadratic formula: \(x=\dfrac{−b{\pm}\sqrt{b^2−4ac}}{2a}\) and for this equation, \(a=1\), \(b=1\), and \(c=2\). Substituting these values into the formula produces

\[\begin{align*}  x&=\dfrac{−1{\pm}\sqrt{1^2−4⋅1⋅(2)}}{2⋅1} \\ &=\dfrac{−1{\pm}\sqrt{1−8}}{2} = \dfrac{−1{\pm}\sqrt{−7}}{2} =\dfrac{−1{\pm}i\sqrt{7}}{2} \nonumber \end{align*}\]

Since the solutions are imaginary, there are no \(x\)-intercepts.

Example \(\PageIndex{8}\): Find the \(y\)- and \(x\)-intercepts of a Standard Form Quadratic

Find the \(y\)- and \(x\)-intercepts of the quadratic \(f(x)=-2(x+3)^2+5\).

Solution

Find the \(y\)-intercept by evaluating \(f(0)\). Notice that the quantity inside the parentheses (\((0+3)=(3)\)) is evaluated FIRST!!!

\( \begin{align*}
f(0) &=-2(0+3)^2+5\\
 &=-2(3)^2+5\\
 &=-2(9)+5\\
 &=-18+5 = -13\\
\end{align*} \)

So the \(y\)-intercept is at \((0,−13)\).

For the \(x\)-intercepts, find all solutions of \(f(x)=0\). Solving a quadratic equation given in standard form, like in this example, is most efficiently accomplished by using the Square Root Property

\( \begin{array}{c}
0 =-2(x+3)^2+5\\
2(x+3)^2 =5\\
(x+3)^2 =\dfrac{5}{2}\\
x+3 =\pm \sqrt{ \dfrac{5}{2}}\\
x = -3 \pm \sqrt{ 2.5 }\\
\end{array} \)

So the \(x\)-intercepts are at \( (-3+\sqrt{2.5}, 0) \) and \( (-3-\sqrt{2.5}, 0) \).

Try It \(\PageIndex{8}\)

Find the \(y\)- and \(x\)-intercepts for the function \(g(x)=13+x^2−6x\).

Answer

\(y\)-intercept at \((0, 13)\), No \(x\)-intercepts

Graph a Quadratic Function

Details on how to find features of a quadratic function have been covered. Now, these features will be used to sketch a graph.

 Graph a quadratic function in the form \(f(x)=ax^2+bx+c\)

1. Determine whether the parabola opens upward \( (a > 0) \) or downward \( (a < 0) \).
2. Find the equation of the axis of symmetry, \( x = h \) where \(h=–\dfrac{b}{2a} \). 
3. Find the vertex, \( (h, k) \), where \( k = f(h) \).
4. Find the \(y\)-intercept, \( f(0) \). Find the point symmetric to the \(y\)-intercept across the axis of symmetry.
5. Find the \(x\)-intercepts. (Set \(f(x)=0\) and solve for \(x\) using factoring, QF or CTS). Find additional points if needed.
6. Graph the parabola.

Example \(\PageIndex{9}\) How to Graph a General Form Quadratic Function Using Properties

Graph \(f(x)=x^{2}-6x+8\) by using its properties.

Solution:

Step 1: Determine whether the parabola opens upward or downward.	Look \(a\) in the equation \(f(x)=x^{2}-6x+8\) Since \(a\) is positive, the parabola opens up.	\(f(x)=x^{2}-6x+8\) \(\color{red}{a=1,\; b=-6, \;c=8}\) The parabola opens upward.
Step 2: Find the axis of symmetry.	\(f(x)=x^{2}-6x+8\) The axis of symmetry is the line \(x=-\frac{b}{2 a}\).	Axis of Symmetry \(x=-\frac{b}{2 a}\) \(x=-\frac{(-6)}{2 \cdot 1}\) \(x=3\) The axis of symmetry is the line \(x=3\).
Step 3: Find the vertex.	The vertex is on the axis of symmetry. Substitute \(x=3\) into the function.	Vertex \(f(x)=x^{2}-6x+8\) \(f(3)=(\color{red}{3}\color{black}{)}^{2}-6(\color{red}{3}\color{black}{)}+8\) \(f(3)=-1\) The vertex is \((3,-1)\).
Step 4: Find the \(y\)-intercept. Find the point symmetric to the \(y\)-intercept across the axis of symmetry.	Find \(f(0)\). Use the axis of symmetry to find a point symmetric to the \(y\)-intercept. The \(y\)-intercept is \(3\) units left of the axis of symmetry, \(x=3\). A point \(3\) units to the right of the axis of symmetry has \(x=6\).	\(y\)-intercept \(f(x)=x^{2}-6 x+8\) \(f(0)=(\color{red}{0}\color{black}{)}^{2}-6(\color{red}{0}\color{black}{)}+8\) \(f(0)=8\) The \(y\)-intercept is \((0,8)\). Point symmetric to \(y\)-intercept: The point is \((6,8)\).
Step 5: Find the \(x\)-intercepts. Find additional points if needed.	Solve \(f(x)=0\). Solve this quadratic equation by factoring.	\(x\)-intercepts \(f(x)=x^{2}-6 x+8\) \(\color{red}{0}\color{black}{=}x^{2}-6x+8\) \(\color{red}{0}\color{black}{=}(x-2)(x-4)\) \(x=2\) or \(x=4\) The \(x\)-intercepts are \((2,0)\) and \((4,0)\).
Step 6: Graph the parabola.	We graph the vertex, intercepts, and the point symmetric to the \(y\)-intercept. We connect these \(5\) points to sketch the parabola.

Try It \(\PageIndex{9}\)

Graph the following quadratic functions by using its properties.

a. \(f(x)=x^{2}+2x-8\) a. Answer opens up, vertex: \((-1,-9)\),  axis: \(x=-1\), intercepts: \((0, -8), (-4,0), (2, 0) \), symm. pt: \((-2, -8) \)

b. \(f(x)=x^{2}-8x+12\) b. Answer opens up, vertex: \((4, -4)\), axis: \(x=4\),  intercepts: \( (0, 12), (2, 0), (6, 0) \), symm.pt: \((8,12)\)

How to: Graph a quadratic function in the form \(f(x)=a(x-h)^2+k\)

1. Determine whether the parabola opens upward \( (a > 0) \) or downward \( (a < 0) \).
2. Find the equation of the axis of symmetry, \( x = h \). 
3. Find the vertex, \( (h, k) \).
4. Find the \(y\)-intercept, \( f(0) \). Find the point symmetric to the \(y\)-intercept across the axis of symmetry.
5. Find the \(x\)-intercepts. (Use the square root property to solve \(a(x-h)^2+h=0\). Find additional points if needed.
6. Graph the parabola.

Example \(\PageIndex{10}\): How to Graph a Vertex Form Quadratic Using Properties

Graph the function \(f(x)=2(x+1)^{2}+3\) by using its properties

Solution:

Step 1: Determine whether the parabola opens upward or downward.	Identify the constants \(a, h, k\). Since \(a=2\), the parabola opens upward.	\(a=2,\; h=-1,\; k=3\) The parabola opens upward.
Step 2: Find the axis of symmetry.	The axis of symmetry is \(x=h\).	The axis of symmetry is the line \(x=-1\).
Step 3: Find the vertex.	The vertex is \((h,k)\).	The vertex is \((-1,3)\).
Step 4: Find the \(y\)-intercept. Find the point symmetric to the \(y\)-intercept across the axis of symmetry.	Find the \(y\)-intercept by finding \(f(0)\). The \(y\)-intercept is \(1\) units right of the axis of symmetry, \(x=-1\). A point \(1\) units to the left of the axis of symmetry has \(x=-2\).	\(f(0)=2(0+1)^2+3=2(1)+3=5\) The \(y\)-intercept is \( (0,5) \). Point symmetric to \(y\)-intercept is \( (-2,5) \)
Step 5: Find the \(x\)-intercepts. Find additional points if needed.	Solve \(f(x)=0\). Use the Square Root Property.   This equation has imaginary solutions, so there are no \(x\)-intercepts	\( \begin{array} {c} 2(x+1)^{2}+3=0 \\ 2(x+1)^{2}=-3 \\ (x+1)^{2}=-3/2 \\ x+1 = \pm \sqrt(-3/2) \\ x=-1 \pm i\sqrt(1.5) \end{array} \) No \(x\) intercepts
Step 6: Graph the parabola.	Graph the vertex, intercepts, and the point symmetric to the \(y\)-intercept. Connect these points to sketch the parabola. Two more points: \( f(1) = 2(1+1)^2+3 = 2(2^2)+3=11\) Therefore, \( (1, 11) \) is on the graph. By symmetry, the point \( (-3, 11) \) is also on the graph

Try It \(\PageIndex{10}\)

Graph the following functions using properties

a. \(f(x)=3(x-1)^{2}+2\) a. Answer opens up, vertex: \((1,2)\),  axis: \(x=1\), intercepts: \((0, 5) \), symm. pt: \((2,5) \)

b. \(f(x)=-2(x-2)^{2}+1\) b. Answer opens down, vertex: \((2,1)\),  axis: \(x=2\), intercepts: \((0, -7), (\approx 1.3,0), (\approx 2.7, 0) \), symm. pt: \((4, -7) \)

Rewrite Quadratics into Vertex Form

As the above examples illustrate, it is often easier to graph a quadratic equation that is in vertex form, rather than in general form. This is particularly true when trying to find \(x\)-intercepts for equations that don't easily factor. There are two different approaches for transforming an equation in general form into an equation in standard (or vertex) form. One method uses the formulas for \(h\) and \(k\). The other method uses Complete the Square. Both will be illustrated below.

Formula method

 How to: Rewrite \(y=ax^2+bx+c\) into vertex form - formula method.

1. Identify constants \( a\) and \(b\).
2. Substitute \( a\) and \(b\) into the formula: \(h=−\dfrac{b}{2a}\).
3. Substitute \(x=h\) into the general form of the quadratic function to find \(k\).
4. Rewrite the quadratic in vertex (standard) form using \(h\) and \(k\). The vertex form of the function is \(f(x)=a(x−h)^2+k \).

Example \(\PageIndex{11}\): Formula method of rewriting into vertex form

Rewrite the quadratic function \(f(x)=2x^2+4x−4\) into vertex form.

Solution

Step 1. Values of the parameters in the general form are \(a=2\), \(b=4\), and \(c=-4\).

Step 2. Solve for \(h\). 

\( h=−\dfrac{b}{2a} =−\dfrac{4}{2(2)} =−1 \)

Step 3. Use the value found for \(h\) to find \(k\).

\(  k=f(h)=f(−1) =2(−1)^2+4(−1)−4 =−6 \)

Step 4. The vertex form of the function is: 

\[\begin{align*}  f(x)&=a(x−h)^2+k \\  f(x)&=2(x+1)^2−6 \end{align*}\]

Try It \(\PageIndex{11}\)

Find the vertex form for the function \(g(x)=13+x^2−6x\). 

Answer

\(g(x)=(x-3)^2 +4 \)

Complete the square method

Another way of transforming \(f(x)=ax^{2}+bx+c\) into the form \(f(x)=a(x−h)^{2}+k\) is by completing the square. The latter form is known as the vertex form or standard form. This approach will also be used when circles are studied.

We must be careful to both add and subtract the number to the SAME side of the function to complete the square. We cannot add the number to both sides as we did when we completed the square with quadratic equations.

Different ways to complete the square.

When we complete the square in a function with a coefficient of \(x^{2}\) that is not one, we have to factor that coefficient from the \(x\)-terms. We do not factor it from the constant term. It is often helpful to move the constant term a bit to the right to make it easier to focus only on the \(x\)-terms.

Once we get the constant we want to complete the square, we must remember to multiply it by the coefficient that was part of the \(x^2\) term before we then subtract it.

 How to: Rewrite \(y=ax^2+bx+c\) into vertex form - complete the square method.

1. Separate the \(x\) terms from the constant.
2. If the coefficient of \(x^{2}\) is not 1, factor it out from the \(x^2\) and \(x\) terms.
3. Find the CTS constant needed to complete the square on the  \(x^2\) and \(x\) terms. 
4. Add the CTS constant to the \(x^2\) and \(x\) terms. Subtract the CTS constant (multiplied by the coefficient of \(x^{2}\) if not 1)
5. Write the trinomial as a binomial square and combine constants outside the binomial square to arrive at the standard form of the function.

Example \(\PageIndex{12}\): CTS method of rewriting into vertex form

Rewrite \(f(x)=−3x^{2}−6x−1\) in the \(f(x)=a(x−h)^{2}+k\) form by completing the square.

Solution:

Step 1. Separate the \(x\) terms from the constant.	\(f(x)=−3x^{2}−6x−1\) \(f(x)=−3x^{2}−6x \qquad \qquad−1\)
Step 2. Factor the coefficient of \(x^{2}, -3\).	\(f(x)=−3(x^{2}+2x) \qquad \qquad−1\)
Step 3. Prepare to complete the square.	\(f(x)=−3(x^{2}+2x \qquad \qquad) −1\)
Take half of \(2\) and then square it to complete the square \((\frac{1}{2}\cdot 2)^{2}=1\)	\(f(x)=-3(x^2+2x + \large\Box ) −1+3 \large\Box \)
Step 4. The constant \(1\) completes the square in the parentheses, but the parentheses is multiplied by \(-3\). So we are really adding \(-3\). We must then add \(3\) to not change the value of the function.
Step 5. Rewrite the trinomial as a square and combine the constants. The function is now in the \(f(x)=a(x-h)^{2}+k\) form.	\( f(x) = -3(x+1)^2+2 \)

Try It \(\PageIndex{12}\)

Rewrite the following functions in the \(f(x)=a(x−h)^{2}+k\) form by completing the square.

a. \(f(x)=−4x^{2}−8x+1\)  a. Answer \(f(x)=-4(x+1)^{2}+5\)

b. \(f(x)=2x^{2}−8x+3\)  b. Answer \(f(x)=2(x-2)^{2}-5\)

Obtain the Equation of a Quadratic Function from a Graph

So far we have started with a function and then found its graph.

Now we are going to reverse the process. Starting with the graph, we will find the function.

 How to: Write a quadratic function in a general form

Given a graph of a quadratic function, write the equation of the function in general form.

1. Identify the horizontal shift of the parabola; this value is \(h\). Identify the vertical shift of the parabola; this value is \(k\).
2. Substitute the values of the horizontal and vertical shift for \(h\) and \(k\). in the function \(f(x)=a(x–h)^2+k\).
3. Substitute the values \(x\) and \(f(x)\) of any point on the graph other than the vertex into the equation from step 2.
4. Solve for the parameter \(a\). The result is the quadratic equation in standard (vertex) form.
5. Expand and simplify to obtain the general form for the quadratic.

Example \(\PageIndex{13}\): Writing the Equation of a Quadratic Function from the Graph

Write an equation for the quadratic function \(g\) in Figure \(\PageIndex{13}\) in standard (vertex) form and then rewrite the result into general form.

Figure \(\PageIndex{13}\): Graph of a parabola with its vertex at \((-2, -3)\).

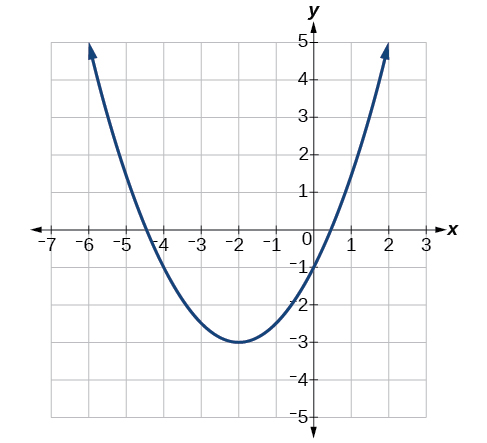
Solution

Since it is quadratic, we start with the \(g(x)=a(x−h)^{2}+k\) form. (Observe the minus sign in front of \(h\)!) The vertex, \((h,k)\), is \((−2,−3)\) so \(h=−2\) and \(k=−3\). Substituting theses values we obtain  \(g(x)=a(x+2)^2–3\).

Substituting the coordinates of a point on the curve, such as \((0,−1)\), we can solve for the parameter \(a\).

\[\begin{align*} −1&=a(0+2)^2−3 \\ 2&=4a \\ a&=\dfrac{1}{2} \end{align*}\]

Using the values found for parameters \(a,\) \(h,\) and \(k,\) write the standard form of the equation:  \(g(x)=\dfrac{1}{2}(x+2)^2–3\).

To write this in general polynomial form, we can expand the formula and simplify terms.

\[\begin{align*} g(x)&=\dfrac{1}{2}(x+2)^2−3 \\ &=\dfrac{1}{2}(x+2)(x+2)−3 \\ &=\dfrac{1}{2}(x^2+4x+4)−3 \\ &=\dfrac{1}{2}x^2+2x+2−3 \\ g(x) &=\dfrac{1}{2}x^2+2x−1 \end{align*}\]

Example \(\PageIndex{14}\)

Determine the quadratic function whose graph is shown.

Solution:

Since it is quadratic, we start with the \(f(x)=a(x−h)^{2}+k\) form.

The vertex, \((h,k)\), is \((−2,−1)\) so \(h=−2\) and \(k=−1\).

\(f(x)=a(x-(-2))^{2}-1 \qquad \longrightarrow \qquad f(x)=a(x+2)^{2}-1\) 

To find \(a\), we use the \(y\)-intercept, \((0,7)\). So \(x=0\) and \(f(0)=7\).

\(7=a(0+2)^{2}-1\)

Solve for \(a\).

\(\begin{array}{l}{7=4 a-1} \\ {8=4 a} \\ {2=a}\end{array}\)

Write the function.

\(f(x)=2(x+2)^{2}-1\)

Try It \(\PageIndex{14}\)

Write the quadratic function in the form \(f(x)=a(x−h)^{2}+k\) for each graph.

a. a. Answer \(f(x)=(x-3)^{2}-4\)

b. b. Answer \(f(x)=(x+3)^{2}-1\)

Try It \(\PageIndex{15}\)

A coordinate grid has been superimposed over the quadratic path of a basketball in Figure \(\PageIndex{15}\). Find an equation for the path of the ball. Does the shooter make the basket?

Figure \(\PageIndex{15}\): Stop motioned picture of a boy throwing a basketball into a hoop to show the parabolic curve it makes.
(credit: modification of work by Dan Meyer)

Answer

The path passes through the origin and has vertex at \((−4, 7)\), so \(h(x)=–\frac{7}{16}(x+4)^2+7\). To make the shot, \(h(−7.5)\) would need to be about 4 but \(h(–7.5){\approx}1.64\); so, he doesn’t make it.

Key Equations

• general form of a quadratic function: \(f(x)=ax^2+bx+c\)
• the quadratic formula: \(x=\dfrac{−b{\pm}\sqrt{b^2−4ac}}{2a}\)
• standard form of a quadratic function: \(f(x)=a(x−h)^2+k\)

Key Concepts

• A polynomial function of degree two is called a quadratic function.
• The graph of a quadratic function is a parabola. A parabola is a U-shaped curve that can open either up or down.
• The axis of symmetry is the vertical line passing through the vertex. The \(x\)-intercepts are the points at which the parabola crosses the \(x\)-axis. The \(y\)-intercept is the point at which the parabola crosses the \(y\)-axis.
• Quadratic functions are often written in general form. Standard or vertex form is useful to easily identify the vertex of a parabola. Either form can be written from a graph.
• The vertex can be found from an equation representing a quadratic function. .
• The domain of a quadratic function is all real numbers. The range varies with the function.
• A quadratic function’s minimum or maximum value is given by the \(y\)-value of the vertex.
• Some quadratic equations must be solved by using the quadratic formula.

Glossary

axis of symmetry
a vertical line drawn through the vertex of a parabola around which the parabola is symmetric; it is defined by \(x=−\dfrac{b}{2a}\).

general form of a quadratic function
the function that describes a parabola, written in the form \(f(x)=ax^2+bx+c\), where \(a,b,\) and \(c\) are real numbers and a≠0.

standard form of a quadratic function
the function that describes a parabola, written in the form \(f(x)=a(x−h)^2+k\), where \((h, k)\) is the vertex.

vertex
the point at which a parabola changes direction, corresponding to the minimum or maximum value of the quadratic function

vertex form of a quadratic function
another name for the standard form of a quadratic function

zeros
in a given function, the values of \(x\) at which \(y=0\), also called roots