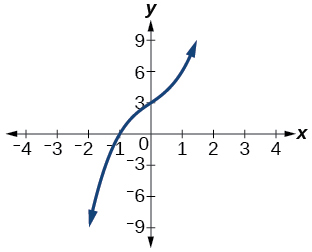3.5e: Exercises - Division of Polynomials
- Page ID
- 45238
A: Concepts
Exercise \(\PageIndex{A}\)
1) If division of a polynomial by a binomial results in a remainder of zero, what can be conclude?
2) If a polynomial of degree \(n\) is divided by a binomial of degree \(1\), what is the degree of the quotient?
- Answers to odd exercises:
-
1. The binomial is a factor of the polynomial.
B: Perform Polynomial Long Division
Exercise \(\PageIndex{B}\)
\( \bigstar \) Use long division to divide. Also specify the quotient and the remainder.
|
3) \((x^2+5x−1)÷(x−1)\) 4) \((2x^2−9x−5)÷(x−5)\) 5) \((3x^2+23x+14)÷(x+7)\) 6) \((4x^2−10x+6)÷(4x+2)\) |
7) \((6x^2−25x−25)÷(6x+5)\) 8) \((−x^2−1)÷(x+1)\) 9) \((2x^2−3x+2)÷(x+2)\) 10) \((x^3−126)÷(x−5)\) |
11) \((3x^2−5x+4)÷(3x+1)\) 12) \((x^3−3x^2+5x−6)÷(x−2)\) 13) \((2x^3+3x^2−4x+15)÷(x+3)\)
|
\( \bigstar \) Divide.
|
14) \(\dfrac{x^{3}-5 x^{2}+x+15}{x-3}\) 15) \(\dfrac{y^{3}-4 y^{2}+6 y-4}{y-2}\) 16) \(\dfrac{x^{5}+3 x+2}{x^{3}+2 x+1}\) |
17) \(\dfrac{2 z^{3}+5 z+8}{z+1}\) 18) \(\dfrac{3 x^{5}-4 x^{3}+3 x^{2}+12 x-10}{x^{2}+2 x-1}\) 19) \(\dfrac{2 y^{5}-3 y^{4}-y^{2}+y+4}{y^{2}+1}\) |
20) \(\dfrac{3 y^{3}-4 y^{2}-3}{y^{2}+5 y+2}\) 21) \(\dfrac{5 x^{4}-3 x^{2}+2}{x^{2}-3 x+5}\)
|
- Answers to odd exercises:
-
3. \(\mathrm{x+6+\dfrac{5}{x−1},
quotient: x+6, remainder: 5}\)5. \(\mathrm{3x+2,
quotient: 3x+2, remainder: 0}\)7. \(\mathrm{x−5,
quotient: x−5, remainder: 0}\)9. \(\mathrm{2x−7+\dfrac{16}{x+2},
quotient: 2x−7, remainder: 16}\)11. \(\mathrm{x−2+\dfrac{6}{3x+1},
quotient: x−2, remainder: 6}\)13. \(\mathrm{2x^2−3x+5,
quotient: 2x^2−3x+5, remainder: 0}\)15. \( y^2-2y+2 \)
17. \( 2z^2-2z+7 + \dfrac{1}{z+1} \)
19. \( 2y^3 -3y^2 -2y +2 +\dfrac{3y+2}{y^2+1} \)
21. \( 5x^2 + 15x + 17 + \dfrac{-24x-83}{x^2-3 x+5} \)
C: Use Long Division to Rewrite a Polynomial
Exercise \(\PageIndex{C}\)
\( \bigstar \) Use polynomial long division to perform the indicated division. Write the polynomial dividend in the form \(p(x) = d(x)q(x) + r(x)\).
|
23. \(\left(4x^2+3x-1 \right) \div (x-3)\) 24) \(\dfrac{x^{3}-4 x^{2}-3 x-10}{x^{2}+x+2}\) 25. \(\left(2x^3-x+1 \right) \div \left(x^{2} +x+1 \right)\) 26) \(\dfrac{2 x^{3}-3 x^{2}+7 x-3}{x^{2}-x+3}\) |
27. \(\left(5x^{4} - 3x^{3} + 2x^{2} - 1 \right) \div \left(x^{2} + 4 \right)\) 28) \(\dfrac{x^{4}+2 x^{3}-x^{2}+x+6}{x+2}\) 29. \(\left(-x^{5} + 7x^{3} - x \right) \div \left(x^{3} - x^{2} + 1 \right)\) 30) \(\dfrac{x^{4}+x^{3}+5 x^{2}+3 x+6}{x^{2}+x-1}\) |
31. \(\left(9x^{3} + 5 \right) \div \left(2x - 3 \right)\) 32) \(\dfrac{x^{4}+2 x^{3}+4 x^{2}+3 x+2}{x^{2}+x+2}\) 33. \(\left(4x^2 - x - 23 \right) \div \left(x^{2} - 1 \right)\) 34) \(\dfrac{2 x^{4}+3 x^{3}+3 x^{2}-5 x-3}{2 x^{2}-x-1}\) |
- Answers to odd exercises:
-
23. \(4x^2+3x-1 = (x-3)(4x+15) + 44\)
25. \(2x^3-x+1 = \left(x^2+x+1\right)(2x-2)+(-x+3)\)
27. \(5x^{4} - 3x^{3} + 2x^{2} - 1 = \left(x^{2} + 4 \right) \left(5x^{2} - 3x - 18 \right) + (12x + 71)\)
29. \(-x^{5} + 7x^{3} - x = \left(x^{3} - x^{2} + 1 \right) \left(-x^{2} - x + 6 \right) + \left(7x^{2} - 6 \right)\)
31. \(9x^{3} + 5 =(2x - 3) \left(\frac{9}{2}x^{2} + \frac{27}{4}x + \frac{81}{8} \right) + \frac{283}{8}\)
33. \(4x^2 - x - 23 = \left(x^{2} - 1 \right)(4) + (-x - 19)\)
D: Perform Synthetic Division
Exercise \(\PageIndex{D}\)
\( \bigstar \) Use synthetic division to divide. Also state the quotient and remainder.
|
35) \(\dfrac{4x^3−33}{x−2}\) 36) \(\dfrac{2x^3+25}{x+3}\) |
37) \(\dfrac{3x^3+2x−5}{x−1}\) 38) \(\dfrac{−4x^3−x^2−12}{x+4}\) |
39) \(\dfrac{x^4−22}{x+2}\)
|
\( \bigstar \)For the exercises below, use synthetic division to find the quotient.
|
40) \((3x^3−2x^2+x−4)÷(x+3)\) 41) \((2x^3−6x^2−7x+6)÷(x−4)\) 42) \((6x^3−10x^2−7x−15)÷(x+1)\) 43) \((4x^3−12x^2−5x−1)÷(2x+1)\) 44) \((9x^3−9x^2+18x+5)÷(3x−1)\) 45) \((3x^3−2x^2+x−4)÷(x+3)\) 46) \((−6x^3+x^2−4)÷(2x−3)\) 47) \((2x^3+7x^2−13x−3)÷(2x−3)\) 48) \((3x^3−5x^2+2x+3)÷(x+2)\) 49) \((4x^3−5x^2+13)÷(x+4)\) 50) \((x^3−3x+2)÷(x+2)\) 51) \((x^3−21x^2+147x−343)÷(x−7)\) |
52) \((x^3−15x^2+75x−125)÷(x−5)\) 53) \((9x^3−x+2)÷(3x−1)\) 54) \((6x^3−x^2+5x+2)÷(3x+1)\) 55) \((x^4+x^3−3x^2−2x+1)÷(x+1)\) 56) \((x^4−3x^2+1)÷(x−1)\) 57) \((x^4+2x^3−3x^2+2x+6)÷(x+3)\) 58) \((x^4−10x^3+37x^2−60x+36)÷(x−2)\) 59) \((x^4−8x^3+24x^2−32x+16)÷(x−2)\) 60) \((x^4+5x^3−3x^2−13x+10)÷(x+5)\) 61) \((x^4−12x^3+54x^2−108x+81)÷(x−3)\) 62) \((4x^4−2x^3−4x+2)÷(2x−1)\) 63) \((4x^4+2x^3−4x^2+2x+2)÷(2x+1)\) |
- Answers to odd exercises:
-
35. \( 4x^2+8x+16 + \frac{-1}{x−2}\),
\(\mathrm{Quotient: 4x^2+8x+16, remainder: −1}\)37. \( 3x^2+3x+5\) ,
\(\mathrm{Quotient: 3x^2+3x+5, remainder: 0}\)39. \( x^3−2x^2+4x−8 + \frac{-6}{x+2}\),
\(\mathrm{Quotient: x^3−2x^2+4x−8, remainder: −6}\)41. \(2x^2+2x+1+\dfrac{10}{x−4}\)
43. \(2x^2−7x+1−\dfrac{2}{2x+1}\)
45. \(3x^2−11x+34−\dfrac{106}{x+3}\)
47. \(x^2+5x+1\)
49. \(4x^2−21x+84−\dfrac{323}{x+4}\)
51. \(x^2−14x+49\)
53. \(3x^2+x+\dfrac{2}{3x−1}\)
55. \(x^3−3x+1\)
57. \(x^3−x^2+2\)
59. \(x^3−6x^2+12x−8\)
61. \(x^3−9x^2+27x−27\)
63. \(2x^3−2x+2\)
E: Use Synthetic Division to Rewrite a Polynomial
Exercise \(\PageIndex{E}\)
\( \bigstar \) For the exercises below, use synthetic division to determine whether the first expression is a factor of the second. If it is, write the second expression as a product of two factors.
|
64) \(x−2, \; 4x^3−3x^2−8x+4\) 65) \(x−2, \; 3x^4−6x^3−5x+10\) |
66) \(x+3, \; −4x^3+5x^2+8\) 67) \(x−2, \; 4x^4−15x^2−4\) |
68) \(x−\dfrac{1}{2}, \; 2x^4−x^3+2x−1\) 69) \(x+\dfrac{1}{3}, \; 3x^4+x^3−3x+1\) |
\( \bigstar \) In the exercises below, use synthetic division to perform the indicated division. Write the polynomial in the form\(p(x) = d(x)q(x) + r(x)\).
|
70. \(\left(3x^2-2x+1 \right) \div \left(x-1\right)\) 71. \(\left(x^2-5 \right) \div \left(x-5\right)\) 72. \(\left(3-4x-2x^2 \right) \div \left(x+1\right)\) 73. \(\left(4x^2-5x +3\right) \div \left(x+3\right)\) 74. \(\left(x^3 + 8 \right) \div \left(x+2\right)\) |
75. \(\left(4x^3 +2x-3 \right) \div \left(x -3\right)\) 76. \(\left(18x^2-15x-25\right) \div \left(x - \frac{5}{3} \right)\) 77. \(\left(4x^2-1 \right) \div \left(x - \frac{1}{2} \right)\) 78. \(\left(2x^3+x^2+2x+1 \right) \div \left(x + \frac{1}{2} \right)\) 79. \(\left(3x^3 - x + 4 \right) \div \left(x - \frac{2}{3} \right)\) |
80. \(\left(2x^3 - 3x +1 \right) \div \left(x - \frac{1}{2} \right)\) 81. \(\left(4x^4-12x^3+13x^2 -12x+9\right) \div \left(x - \frac{3}{2} \right)\) 82. \(\left(x^4-6x^2+9 \right) \div \left(x -\sqrt{3} \right)\) 83. \(\left(x^6-6x^4+12x^2-8\right) \div \left(x +\sqrt{2} \right)\)
|
- Answers to odd exercises:
-
65. Yes \((x−2)(3x^3−5)\)
67. Yes \((x−2)(4x^3+8x^2+x+2)\)
69. No
71. \(\left(x^2-5 \right)= \left(x-5\right)(x+5) + 20\)
73. \(\left(4x^2-5x +3\right) = \left(x+3\right)(4x-17)+54\)
75. \(\left(4x^3 +2x-3 \right) = \left(x -3\right) \left(4x^2+12x+38\right) + 111\)
77. \(\left(4x^2-1 \right) = \left(x - \frac{1}{2} \right)(4x+2)+0\)
79. \(\left(3x^3 - x + 4 \right) = \left(x - \frac{2}{3} \right) \left(3x^2+2x+\frac{1}{3}\right) + \frac{38}{9}\)
81. \(\left(4x^4-12x^3+13x^2 -12x+9\right) = \left(x - \frac{3}{2} \right) \left(4x^3-6x^2+4x-6 \right)+0\)
83. \(\left(x^6-6x^4+12x^2-8\right) = \left(x +\sqrt{2} \right) \left(x^5-\sqrt{2} \, x^4-4x^3+4\sqrt{2} \, x^2+4x-4\sqrt{2}\right) + 0\)
F: Synthetic Division with Complex Numbers
Exercise \(\PageIndex{F}\)
\( \bigstar \) For the exercises below, use synthetic division to determine the quotient involving a complex number.
| 85) \(\dfrac{x+1}{x−i}\) | 86) \(\dfrac{x^2+1}{x−i}\) | 87) \(\dfrac{x+1}{x+i}\) | 88) \(\dfrac{x^2+1}{x+i}\) | 89) \(\dfrac{x^3+1}{x−i}\) |
\( \bigstar \) Find the remainder.
|
90) \((x^4−9x^2+14)÷(x−2)\) 91) \((3x^3−2x^2+x−4)÷(x+3)\) 92) \((x^4+5x^3−4x−17)÷(x+1)\) 93) \((−3x^2+6x+24)÷(x−4)\) |
94) \((5x^5−4x^4+3x^3−2x^2+x−1)÷(x+6)\) 95) \((x^4−1)÷(x−4)\) 96) \((3x^3+4x^2−8x+2)÷(x−3)\) 97) \((4x^3+5x^2−2x+7)÷(x+2)\) |
- Answers to odd exercises:
-
85. \(1+\dfrac{1+i}{x−i}\)
87. \(1+\dfrac{1−i}{x+i}\)
89. \(x^2+ix−1+\dfrac{1−i}{x−i}\)
91. \(−106\), \(f(2) = -106\)
93. \(0\), \(f(4) = 0 \)
95. \(255\), \(f(4) = 255 \)
97. \(−1\), \(f(-2) = -1 \)
G: Construct a polynomial from a graph and a given Factor
Exercise \(\PageIndex{G}\)
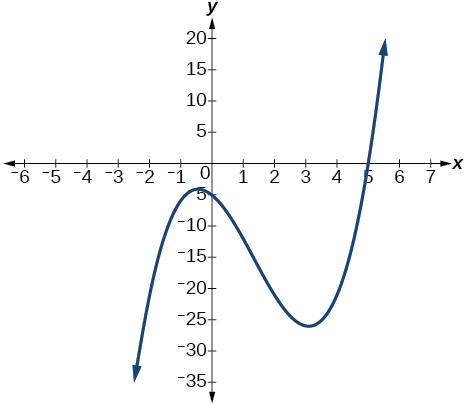
\( \bigstar \) Use the graph of the third-degree polynomial and one factor to write the factored form of the polynomial suggested by the graph. The leading coefficient is one.
|
98) Factor is \(x^2−x+3\)
|
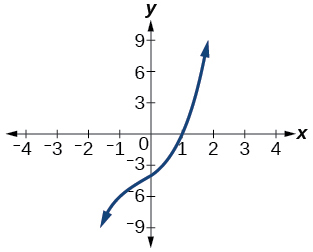
99) Factor is \((x^2+2x+4)\)
|
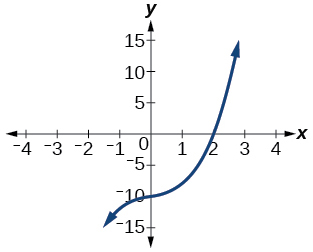
100) Factor is \(x^2+2x+5\)
|
|
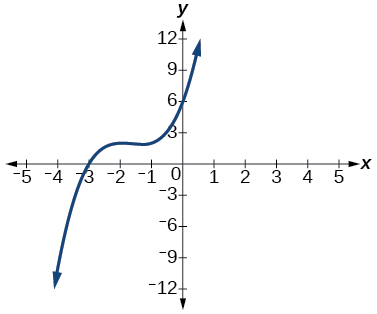
101) Factor is \(x^2+2x+2\)
|
102) Factor is \(x^2+x+1\)
|
|
- Answers to odd exercises:
-
99. \((x−1)(x^2+2x+4)\) 101. \((x+3)(x^2+2x+2)\)