4.3: Logarithmic Functions
- Page ID
- 34904
Learning Objectives
- Convert from logarithmic to exponential form.
- Convert from exponential to logarithmic form.
- Evaluate logarithms.
- Use common logarithms.
- Use natural logarithms.
In 2010, a major earthquake struck Haiti, destroying or damaging over 285,000 homes. One year later, another, stronger earthquake devastated Honshu, Japan, destroying or damaging over 332,000 buildings. Even though both caused substantial damage, the earthquake in 2011 was 100 times stronger than the earthquake in Haiti. How do we know? The magnitudes of earthquakes are measured on a scale known as the Richter Scale. The Haitian earthquake registered a 7.0 on the Richter Scale whereas the Japanese earthquake registered a 9.0.
The Richter Scale is a base-ten logarithmic scale. In other words, an earthquake of magnitude \(8\) is not twice as great as an earthquake of magnitude \(4\). It is \(10^{8−4}=10^4=10,000\) times as great! In this lesson, we will investigate the nature of the Richter Scale and the base-ten function upon which it depends.
Logarithmic Functions Defined
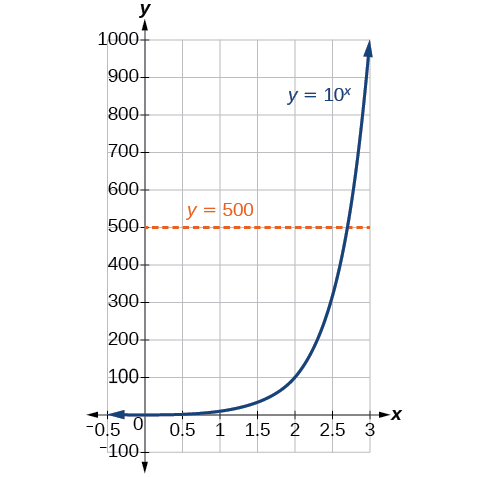 In order to analyze the magnitude of earthquakes or compare the magnitudes of two different earthquakes, we need to be able to convert between logarithmic and exponential form. For example, suppose the amount of energy released from one earthquake were 500 times greater than the amount of energy released from another. We want to calculate the difference in magnitude. The equation that represents this problem is \(10^x=500\), where \(x\) represents the difference in magnitudes on the Richter Scale. How would we solve for \(x\)?
In order to analyze the magnitude of earthquakes or compare the magnitudes of two different earthquakes, we need to be able to convert between logarithmic and exponential form. For example, suppose the amount of energy released from one earthquake were 500 times greater than the amount of energy released from another. We want to calculate the difference in magnitude. The equation that represents this problem is \(10^x=500\), where \(x\) represents the difference in magnitudes on the Richter Scale. How would we solve for \(x\)?
We have not yet learned a method for solving exponential equations. None of the algebraic tools discussed so far is sufficient to solve \(10^x=500\). We know that \({10}^2=100\) and \({10}^3=1000\), so it is clear that \(x\) must be some value between 2 and 3, since \(y={10}^x\) is increasing. We can examine a graph, as in the figure to the right, to better estimate the solution.
Estimating from a graph, however, is imprecise. To find an algebraic solution, we must introduce a new function. Observe that the graph of \(y = 10^x\) passes the horizontal line test. The exponential function \(y=b^x\) is one-to-one, so its inverse, \(x=b^y\) is also a function. As is the case with all inverse functions, we simply interchange \(x\) and \(y\) and solve for \(y\) to find the inverse function. To represent \(y\) as a function of \(x\), we use a logarithmic function of the form \(y={\log}_b(x)\). The base \(b\) logarithm of a number is the exponent by which we must raise \(b\) to get that number.
We read a logarithmic expression as, “The logarithm with base \(b\) of \(x\) is equal to \(y\),” or, simplified, “log base \(b\) of \(x\) is \(y\).” We can also say, “\(b\) raised to the power of \(y\) is \(x\),” because logs are exponents. For example, the base \(2\) logarithm of \(32\) is \(5\), because \(5\) is the exponent we must apply to \(2\) to get \(32\). Since \(2^5=32\), we can write \({\log}_232=5\). We read this as “log base \(2\) of \(32\) is \(5\).”
We can express the relationship between logarithmic form and its corresponding exponential form as follows:
\[\begin{align*} \log_b(x)=y\Leftrightarrow b^y=x, \qquad \qquad b > 0, \:\:b\neq 1 \end{align*}\]
Note that the base \(b\) is always positive.
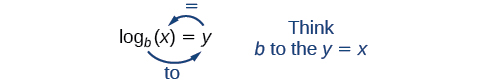
Because logarithm is a function, it is most correctly written as \(\log_b(x)\), using parentheses to denote function evaluation, just as we would with \(f(x)\). However, when the input is a single variable or number, it is common to see the parentheses dropped and the expression written without parentheses, as \(\log_bx\). Note that many calculators require parentheses around the \(x\). We can illustrate the notation of logarithms as follows:
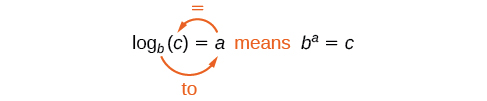
Notice that, comparing the logarithm function and the exponential function, the input and the output are switched. This means \(y=\log_b(x)\) and \(y=b^x\) are inverse functions.
DEFINITION OF THE LOGARITHMIC FUNCTION
A logarithm base \(b\) of a positive number \(x\) satisfies the following definition.
\[\begin{align*} y={\log}_b(x) \qquad \text{ is equivalent to } \qquad b^y=x \qquad\qquad \text{for } x>0,\:\: b>0,\:\: b≠1 \end{align*} \]
- We read \({\log}_b(x)\) as “log base \(b\) of \(x\)." It is equivalent to saying "the exponent on \(b\) to get \(x\)."
- The logarithm \(y\) is the exponent to which \(b\) must be raised to get \(x\).
Also, since the logarithmic and exponential functions switch the \(x\) and \(y\) values, the domain and range of the exponential function are interchanged for the logarithmic function. Therefore, for the parent logarithm function \(y={\log}_b(x) \),
- The domain of the logarithm function with base \(b\) is \((0,\infty)\).
- The range of the logarithm function with base \(b\) is \((−\infty,\infty)\).
 Can we take the logarithm of a negative number?
Can we take the logarithm of a negative number?
No. Because the base of an exponential function is always positive, no power of that base can ever be negative. We can never take the logarithm of a negative number. Also, we cannot take the logarithm of zero. Calculators may output a log of a negative number when in complex mode, but the log of a negative number is not a real number.
Convert from Logarithmic to Exponential Form
![]() How to: Given an equation in logarithmic form \({\log}_b(x)=y\), convert it to exponential form
How to: Given an equation in logarithmic form \({\log}_b(x)=y\), convert it to exponential form
- Examine the equation \(p={\log}_b a\) and identify the base \(b\), the power \(p\), and the log argument \(a\).
- Rewrite \({\log}_b a =p \) as \(b^p=a\).
Notice the result of taking the log of something is an exponent; the result of exponentiation is a log argument
Example \(\PageIndex{1}\): Convert from Logarithmic Form to Exponential Form
Write the following logarithmic equations in exponential form.
| a. \( \log_6(\sqrt{6})=\dfrac{1}{2}\) | b. \({\log}_3(9)=2\) |
Solution
First, identify the values of \(b\), \(p\), and \(a\). Then, write the equation in the form \(b^y=x\).
- \({\log}_6(\sqrt{6})=\dfrac{1}{2}\) \( \qquad\) Here, the base \(b=6\), the power \(p=\dfrac{1}{2}\), and the argument \(a=\sqrt{6}\).
Therefore, the equation \({\log}_6(\sqrt{6})=\dfrac{1}{2}\) is equivalent to \(6^{\tfrac{1}{2}}=\sqrt{6}\)
- \({\log}_3(9)=2\) \( \qquad\) Here, the base \(b=3\), the power \(p=2\), and the argument \(a=9\).
Therefore, the equation \({\log}_3(9)=2\) is equivalent to \(3^2=9\)
![]() Try It \(\PageIndex{1}\)
Try It \(\PageIndex{1}\)
Write the following logarithmic equations in exponential form.
|
a. \({\log}_{10}(1,000,000)=6\)
|
b. \({\log}_5(25)=2\)
|
Convert from Exponential to Logarithmic Form
![]() How to: Given an equation in exponential form \(b^x = y\), convert it to logarithmic form
How to: Given an equation in exponential form \(b^x = y\), convert it to logarithmic form
- Examine the equation \(b^p=a\) and identify the base \(b\), the power \(p\), and the answer\(a\) (which will be the log argument).
- Rewrite \(b^p=a\) as \({\log}_b a =p \) .
Example \(\PageIndex{2}\): Convert from Exponential Form to Logarithmic Form
Write the following exponential equations in logarithmic form.
| a. \(2^3=8\) | b. \(5^2=25\) | c. \({10}^{−4}=\dfrac{1}{10,000}\) |
Solution
First, identify the values of \(b\), \(p\), and \(a\). Then, write the equation in the form \(x=\log_b (y) \).
- \(2^3=8\) \( \qquad\) Here, \(b=2\), \(p=3\),and \(a=8\).
Therefore, the equation \(2^3=8\) is equivalent to \({\log}_2(8)=3\).
- \(5^2=25\) \( \qquad\) Here, \(b=5\), \(p=2\),and \(a=25\).
Therefore, the equation \(5^2=25\) is equivalent to \({\log}_5(25)=2\).
- \({10}^{−4}=\dfrac{1}{10,000}\) \( \qquad\) Here, \(b=10\), \(p=−4\),and \(a=\dfrac{1}{10,000}\).
Therefore, the equation \({10}^{−4}=\dfrac{1}{10,000}\) is equivalent to \(\log_{10} \left( \dfrac{1}{10,000} \right)=−4\).
![]() Try It \(\PageIndex{2}\)
Try It \(\PageIndex{2}\)
Write the following exponential equations in logarithmic form.
|
a. \(3^2=9\)
|
b. \(5^3=125\)
|
c. \(2^{−1}=\dfrac{1}{2}\)
|
Evaluate Logarithms
Knowing the squares, cubes, and roots of numbers allows us to evaluate many logarithms mentally. For example, consider \({\log}_28\). We ask, “To what exponent must \(2\) be raised in order to get 8?” Because we already know \(2^3=8\), it follows that \({\log}_28=3\).
Now consider solving \({\log}_749\) and \({\log}_327\) mentally.
- We ask, “To what exponent must \(7\) be raised in order to get \(49\)?” We know \(7^2=49\). Therefore, \({\log}_749=2\)
- We ask, “To what exponent must \(3\) be raised in order to get \(27\)?” We know \(3^3=27\). Therefore, \(\log_{3}27=3\)
Even some seemingly more complicated logarithms can be evaluated without a calculator. For example, let’s evaluate \(\log_{\ce{2/3}} \frac{4}{9}\) mentally.
- We ask, “To what exponent must \(\ce{2/3}\) be raised in order to get \(\ce{4/9}\)? ”
We know \(2^2=4\) and \(3^2=9\), so \( \left( \dfrac{2}{3} \right)^2=\dfrac{4}{9}. \) Therefore, \(\log_\frac{2}{3} \left( \dfrac{4}{9} \right)=2. \)
![]() How to: Given a logarithm of the form \(y={\log}_b(x)\), evaluate it mentally
How to: Given a logarithm of the form \(y={\log}_b(x)\), evaluate it mentally
- Rewrite the argument \(x\) as a power of \(b\): \(b^y=x\).
- Use previous knowledge of powers of \(b\) identify \(y\) by asking, “To what exponent should \(b\) be raised in order to get \(x\)?”
Example \(\PageIndex{3}\): Evaluate Logarithms Mentally
Solve \(y={\log}_4(64)\) without using a calculator.
Solution
First we rewrite the logarithm in exponential form: \(4^y=64\).
Next, we ask, “To what exponent must \(4\) be raised in order to get \(64\)?”
We know \(4^3=64\). Therefore, \(\log_4(64)=3\)
![]() Try It \(\PageIndex{3}\)
Try It \(\PageIndex{3}\)
Solve \(y={\log}_{121}(11)\) without using a calculator.
- Answer
-
\({\log}_{121}(11)=\dfrac{1}{2}\) (recalling that \(\sqrt{121}={(121)}^{\tfrac{1}{2}}=11)\)
Example \(\PageIndex{4}\): Evaluate the Logarithm of a Reciprocal
Evaluate \(y={\log}_3 \left (\dfrac{1}{27} \right )\) without using a calculator.
Solution
First rewrite the logarithm in exponential form: \(3^y=\dfrac{1}{27}\).
Next ask, “To what exponent must \(3\) be raised in order to get \(\dfrac{1}{27}\)?”
We know \(3^3=27\), so \(\dfrac{1}{3^3} = \dfrac{1}{27} .\) Therefore, \({\log}_3 \left (\dfrac{1}{27} \right )=−3\).
![]() Try It \(\PageIndex{4}\)
Try It \(\PageIndex{4}\)
Evaluate \(y={\log}_2 \left (\dfrac{1}{32} \right )\) without using a calculator.
- Answer
-
\({\log}_2 \left (\dfrac{1}{32} \right )=−5\)
Common Logarithms
Sometimes we may see a logarithm written without a base. In this case, we assume that the base is \(10\). In other words, the expression \(\log(x)\) means \({\log}_{10}(x)\). We call a base 10 logarithm a common logarithm. Common logarithms are used to measure the Richter Scale mentioned at the beginning of the section. Scales for measuring the brightness of stars and the pH of acids and bases also use common logarithms.
DEFINITION OF THE COMMON LOGARITHM
A common logarithm is a logarithm with base \(10\). We write \({\log}_{10}(x)\) simply as \(\log(x)\). The common logarithm of a positive number \(x\) satisfies the following definition.
\[\begin{align*} y={\log}(x) \qquad \text{ is equivalent to } \qquad {10}^y=x \qquad\qquad\qquad \text{for } x>0 \end{align*}\]
We read \(\log(x)\) as “log base \(10\) of \(x\).” The logarithm \(y\) is the exponent to which \(10\) must be raised to get \(x\).
![]() How to: Given a common logarithm of the form \(y=\log(x)\), evaluate it mentally
How to: Given a common logarithm of the form \(y=\log(x)\), evaluate it mentally
- Rewrite the argument \(x\) as a power of \(10\): \({10}^y=x\).
- Use previous knowledge of powers of \(10\) to identify \(y\) by asking, “To what exponent must \(10\) be raised to get \(x\)?”
Example \(\PageIndex{5}\): Find the Value of a Common Logarithm Mentally
Evaluate \(y=\log(1000)\) without using a calculator.
Solution
First we rewrite the logarithm in exponential form: \({10}^y=1000\).
Next, we ask, “To what exponent must \(10\) be raised in order to get \(1000\)?” We know \({10}^3=1000\)
Therefore, \(\log(1000)=3\).
![]() Try It \(\PageIndex{5}\)
Try It \(\PageIndex{5}\)
Evaluate \(y=\log(1,000,000)\).
- Answer
-
\(\log(1,000,000)=6\)
![]() How to: Given a common logarithm with the form \(y=\log(x)\), evaluate it using a calculator
How to: Given a common logarithm with the form \(y=\log(x)\), evaluate it using a calculator
- Press [LOG].
- Enter the value given for \(x\), followed by [ ) ].
- Press [ENTER].
Example \(\PageIndex{6}\): Find the Value of a Common Logarithm Using a Calculator
Evaluate \(y=\log(321)\) to four decimal places using a calculator.
Solution
Press [LOG]. Enter 321, followed by [ ) ]. Press [ENTER]. Rounding to four decimal places, \(\log(321)≈2.5065\).
Analysis
Note that \({10}^2=100\) and that \({10}^3=1000\) and \(321\) is between \(100\) and \(1000\). This gives us the following:
\(100<321<1000\)
\( \log(100) < \log(321) < \log(1000) \)
\(2<2.5065<3\)
![]() Try It \(\PageIndex{6}\)
Try It \(\PageIndex{6}\)
Evaluate \(y=\log(123)\) to four decimal places using a calculator.
- Answer
-
\(\log(123)≈2.0899\)
Example \(\PageIndex{7}\): Application of Common logarithms in a Real-World Exponential Model
The amount of energy released from one earthquake was \(500\) times greater than the amount of energy released from another. The equation \({10}^x=500\) represents this situation, where \(x\) is the difference in magnitudes on the Richter Scale. To the nearest thousandth, what was the difference in magnitudes?
Solution
We begin by rewriting the exponential equation in logarithmic form.
\({10}^x=500 \longleftrightarrow \log(500)=x\)
Next we evaluate the logarithm using a calculator:
Press [LOG]. Enter 500, followed by [ ) ]. Press [ENTER]. To the nearest thousandth, \(\log(500)≈2.699\).
The difference in magnitudes was about \(2.699\).
![]() Try It \(\PageIndex{7}\)
Try It \(\PageIndex{7}\)
The amount of energy released from one earthquake was \(8,500\) times greater than the amount of energy released from another. The equation \({10}^x=8500\) represents this situation, where \(x\) is the difference in magnitudes on the Richter Scale. To the nearest thousandth, what was the difference in magnitudes?
- Answer
-
The difference in magnitudes was about \(3.929\).
Natural Logarithms
The most frequently used base for logarithms is \(e\). Base \(e\) logarithms are important in calculus and some scientific applications; they are called natural logarithms. The base \(e\) logarithm, \({\log}_e(x)\), has its own notation, \(\ln(x)\). Most values of \(\ln(x)\) can be found only using a calculator. The major exception is that, because the logarithm of \(1\) is always \(0\) in any base, \(\ln1=0\). For other natural logarithms, we can use the \(\ln\) key that can be found on most scientific calculators. We can also find the natural logarithm of any power of \(e\) using the inverse property of logarithms.
DEFINITION OF THE NATURAL LOGARITHM
A natural logarithm is a logarithm with base \(e\). We write \({\log}_e(x)\) simply as \(\ln(x)\). The natural logarithm of a positive number \(x\) satisfies the following definition.
\(y = \ln(x) \qquad \) is equivalent to \( \qquad e^y=x \qquad \qquad \text{for } x>0 \)
We read \(\ln(x)\) as “the natural logarithm of \(x\).”
The logarithm \(y\) is the exponent to which \(e\) must be raised to get \(x\).
Since the functions \(y=e^x\) and \(y=\ln(x)\) are inverse functions, \(\ln(e^x)=x\) for all \(x\) and \(e^{\ln (x)}=x\) for \(x>0\).
![]() How to: Given a natural logarithm with the form \(y=\ln(x)\), evaluate it using a calculator
How to: Given a natural logarithm with the form \(y=\ln(x)\), evaluate it using a calculator
- Press [LN].
- Enter the value given for \(x\), followed by [ ) ].
- Press [ENTER].
Example \(\PageIndex{8}\): Evaluate a Natural Logarithm Using a Calculator
Evaluate \(y=\ln(500)\) to four decimal places using a calculator.
Solution
Press [LN]. Enter 500, followed by [ ) ]. Press [ENTER]. Rounding to four decimal places, \(\ln(500)≈6.2146\)
![]() Try It \(\PageIndex{8}\)
Try It \(\PageIndex{8}\)
Evaluate \(\ln(−500)\).
- Answer
-
It is not possible to take the logarithm of a negative number in the set of real numbers.
Key Equations
| Definition of the logarithmic function | For \(x>0\), \(b>0\), \(b≠1\), \(y={\log}_b(x)\) if and only if \(b^y=x\). |
| Definition of the common logarithm | For \(x>0\), \(y=\log(x)\) if and only if \({10}^y=x\). |
| Definition of the natural logarithm | For \(x>0\), \(y=\ln(x)\) if and only if \(e^y=x\). |
Key Concepts
- Exponential and logarithmic functions are inverses of each other.
- Logarithmic equations can be written in an equivalent exponential form, using the definition of a logarithm.
- Exponential equations can be written in their equivalent logarithmic form using the definition of a logarithm.
- Logarithmic functions with base \(b\) can be evaluated mentally using previous knowledge of powers of \(b\).
- Common logarithms can be evaluated mentally using previous knowledge of powers of \(10\).
- When common logarithms cannot be evaluated mentally, a calculator can be used.
- Real-world exponential problems with base \(10\) can be rewritten as a common logarithm and then evaluated using a calculator.
- Natural logarithms can be evaluated using a calculator.
Contributors
Jay Abramson (Arizona State University) with contributing authors. Textbook content produced by OpenStax College is licensed under a Creative Commons Attribution License 4.0 license. Download for free at https://openstax.org/details/books/precalculus.

