4.7e: Exercises - Exponential Applications
- Page ID
- 44982
A: Concepts
Exercise \(\PageIndex{A}\)
1) With what kind of exponential model would half-life be associated? What role does half-life play in these models?
2) What is carbon dating? Why does it work? Give an example in which carbon dating would be useful.
3) With what kind of exponential model would doubling time be associated? What role does doubling time play in these models?
4) Define Newton’s Law of Cooling. Then name at least three real-world situations where Newton’s Law of Cooling would be applied.
5) What is an order of magnitude? Why are orders of magnitude useful? Give an example to explain.
7) A doctor and injects a patient with \(13\) milligrams of radioactive dye that decays exponentially. After \(12\) minutes, there are \(4.75\) milligrams of dye remaining in the patient’s system. Which is an appropriate model for this situation?
a. \(f(t)=13(0.0805)^t\) \(\quad\) b. \(f(t)=13e^{0.9195t}\) \(\quad\) c. \(f(t)=13e^{(-0.0839t)}\) \(\quad\) d. \(f(t)=\frac{4.75}{1+13e^{-0.83925t}}\)
9) What situations are best modeled by a logistic equation? Give an example, and state a case for why the example is a good fit.
10) What is a carrying capacity? What kind of model has a carrying capacity built into its formula? Why does this make sense?
- Answers to odd exercises:
-
1. Half-life is a measure of decay and is thus associated with exponential decay models. The half-life of a substance or quantity is the amount of time it takes for half of the initial amount of that substance or quantity to decay.
3. Doubling time is a measure of growth and is thus associated with exponential growth models. The doubling time of a substance or quantity is the amount of time it takes for the initial amount of that substance or quantity to double in size.
5. An order of magnitude is the nearest power of ten by which a quantity exponentially grows. It is also an approximate position on a logarithmic scale; Sample response: Orders of magnitude are useful when making comparisons between numbers that differ by a great amount. For example, the mass of Saturn is \(95\) times greater than the mass of Earth. This is the same as saying that the mass of Saturn is about \(10^2\) times, or \(2\) orders of magnitude greater, than the mass of Earth.
7. C
9. Logistic models are best used for situations that have limited values. For example, populations cannot grow indefinitely since resources such as food, water, and space are limited, so a logistic model best describes populations.
B: Compound Interest
Exercise \(\PageIndex{B}\)
Find current amount
- Billy’s grandfather invested in a savings bond that earned \(5.5\)% annual interest that was compounded annually. Currently, \(30\) years later, the savings bond is valued at $\(10,000\). Determine what the initial investment was.
- Given a yearly interest rate of 3.5% and an initial principle of $100,000, find the amount \(A\) accumulated in 5 years for interest that is compounded a. daily, b., monthly, c. quarterly, and d. yearly.
- Starting with $100,000 invested at an annual interest rate of \(5.5\)% compounded continuously, find the amount accumulated after 5 years.
- In 1935 Frank opened an account earning \(3.8\)% annual interest that was compounded quarterly. He rediscovered this account while cleaning out his garage in 2005. If the account is now worth $\(11,294.30\), how much was his initial deposit in 1935?
Find principal
- Given that the bank is offering \(4.2\)% annual interest compounded monthly, what principal is needed to earn $\(25,000\) in interest for one year?
- Given that the bank is offering \(3.5\)% annual interest compounded continuously, what principal is needed to earn $\(12,000\) in interest for one year?
Find interest rate
- Find the annual interest rate at which an account earning continuously compounding interest has a doubling time of \(9\) years.
- Find the annual interest rate at which an account earning interest that is compounded monthly has a doubling time of \(10\) years.
- Alice invests $\(15,000\) at age \(30\) from the signing bonus of her new job. She hopes the investments will be worth $\(30,000\) when she turns \(40\). If the interest compounds continuously, approximately what rate of growth will she need to achieve her goal?
- Sung Lee invests $\(5,000\) at age \(18\). He hopes the investments will be worth $\(10,000\) when he turns \(25\). If the interest compounds continuously, approximately what rate of growth will he need to achieve his goal? Is that a reasonable expectation?
Find time
- Jill invested $\(1,450\) in an account earning \(4 \frac{5}{8}\)% annual interest that is compounded monthly.
- How much will be in the account after \(6\) years?
- How long will it take the account to grow to $\(2,200\)?
- James invested $\(825\) in an account earning \(5 \frac{2}{5}\)% annual interest that is compounded monthly.
- How much will be in the account after \(4\) years?
- How long will it take the account to grow to $\(1,500\)?
- Bill wants to grow his $\(75,000\) inheritance to $\(100,000\) before spending any of it. How long will this take if the bank is offering \(5.2\)% annual interest compounded quarterly?
- Mary needs $\(25,000\) for a down payment on a new home. If she invests her savings of $\(21,350\) in an account earning \(4.6\)% annual interest that is compounded semi-annually, how long will it take to grow to the amount that she needs?
- Joe invested his $\(8,700\) savings in an account earning \(6 \frac{3}{4}\)% annual interest that is compounded continuously. How long will it take to earn $\(300\) in interest?
- Miriam invested $\(12,800\) in an account earning \(5 \frac{1}{4}\)% annual interest that is compounded monthly. How long will it take to earn $\(1,200\) in interest?
- Raul invested $\(8,500\) in an online money market fund earning \(4.8\)% annual interest that is compounded continuously.
- How much will be in the account after \(2\) years?
- How long will it take the account to grow to $\(10,000\)?
- Ian deposited $\(500\) in an account earning \(3.9\)% annual interest that is compounded continuously.
- How much will be in the account after \(3\) years?
- How long will it take the account to grow to $\(1,500\)?
Find doubling time
- Jose invested his $\(3,500\) bonus in an account earning \(5 \frac{1}{2}\)% annual interest that is compounded quarterly. How long will it take to double his investment?
- Maria invested her $\(4,200\) savings in an account earning \(6 \frac{3}{4}\)% annual interest that is compounded semi-annually. How long will it take to double her savings?
- Calculate the doubling time of an investment made at \(7\)% annual interest that is compounded: (a) monthly (b) continuously
- Coralee invests $\(5,000\) in an account that compounds interest monthly and earns \(7\)%. How long will it take for her money to double?
- If money is invested in an account earning \(3.85\)% annual interest that is compounded continuously, how long will it take the amount to double?
- Calculate the doubling time of an investment that is earning continuously compounding interest at an annual interest rate of: (a) \(4\)% (b) \(6\)%
Find Tripling time
- Jill invested $\(1,450\) in an account earning \(4 \frac{5}{8}\)% annual interest that is compounded monthly.
- Find the amount accumulated after 5 years and 10 years.
- Determine how long it takes for the original investment to triple.
- Alice invested her savings of $\(7,000\) in an account earning \(4.5\)% annual interest that is compounded monthly. How long will it take the account to triple in value?
- Mary invested her $\(42,000\) bonus in an account earning \(7.2\)% annual interest that is compounded continuously. How long will it take the account to triple in value?
- Answers to odd exercises:
-
11. $\(2,006.44\)
13. Approximately $131,653
15. $\(583,867\)
17. \(7.7\)%
19. \(6.9\)%
21. (a) $\(1,912.73\) (b) \(9\) years
23. \(5.6\) years
25. \(\frac{1}{2}\) year
27. (a) $\(9,356.45 \) (b) \(3.4\) years
29. \(12.7\) years
31. (a) \(9.93\) years (b) \(9.90\) years
33. \(18\) years
37. \(24.5\) years
C: Exponential Growth
Exercise \(\PageIndex{C}\)
Find current amount
41. The number of bacteria N in a culture after t days can be modeled by the function \(N(t)=1300⋅(2)^{t/4}\). Find the number of bacteria present after 15 days.
42. A research student is working with a culture of bacteria that doubles in size every twenty minutes. The initial population count was \(1350\) bacteria. Rounding to five significant digits, write an exponential equation representing this situation. To the nearest whole number, what is the population size after \(3\) hours?
43. Suppose that the population of a certain town grows at an annual rate of 6%. If the population is currently 5, 000, what will it be in 7 years? Round your answer to the nearest integer.
44. Suppose that the population of a certain town grows at an annual rate of 4%. If the population is currently 1, 000, what will it be in 3 years? Round your answer to the nearest integer.
Find initial amount
46. A biologist recorded a count of \(360\) bacteria present in a culture after \(5\) minutes and \(1000\) bacteria present after \(20\) minutes.
(a) To the nearest whole number, what was the initial population in the culture?
(b) Rounding to six significant digits, write an exponential equation representing this situation. To the nearest minute, how long did it take the population to double?
47. Suppose that the population of a certain town grows at an annual rate of 9%. If the population grows to 7, 000 in 5 years, what was the original population? Round your answer to the nearest integer.
48. Suppose that the population of a certain town grows at an annual rate of 2%. If the population grows to 9, 000 in 4 years, what was the original population? Round your answer to the nearest integer.
Find growth rate
49. A bacterial colony grown in a lab is known to double in number in 12 hours. Suppose, initially, there are 1000 bacteria present.
a. Use the exponential function \(Q=Q_0e^{kt}\) to determine \(k\), the growth rate of the bacteria. Round to four decimal places.
b. Determine approximately how long it takes for 200,000 bacteria to grow.
50. The rabbit population on a game reserve doubles every 6 months. Suppose there were 120 rabbits initially.
a. Use the exponential function \(P=P_0a^t\) to determine the growth factor \(a\). Round to four decimal places.
b. Use the function in part a. to determine approximately how long it takes for the rabbit population to reach 3500.
Find time
51. Suppose that the population of a certain town grows at an annual rate of 8%. If the population is currently 2,000, how many years will it take for it to reach 7,000? Round your answer to the nearest hundredth.
52. Suppose that the population of a certain town grows at an annual rate of 4%. If the population is currently 7,000, how many years will it take for it to reach 17,000? Round your answer to the nearest hundredth.
Find doubling time
53. According to the World Bank, at the end of 2013 \((t=0)\) the U.S. population was 316 million and was increasing according to the following model below where P is measured in millions of people and t is measured in years after 2013.
\(P(t)=316e^{0.0074t}\),
a. Based on this model, what will be the population of the United States in 2020?
b. Determine when the U.S. population will be twice what it is in 2013.
54. Suppose that the population of a certain town grows at an annual rate of 8%. If the population is currently 4,000, how many years will it take for it to double? Round your answer to the nearest hundredth.
55. Suppose that the population of a certain town grows at an annual rate of 2%. If the population is currently 7,000, how many years will it take for it to double? Round your answer to the nearest hundredth.
- Answers to odd exercises:
-
11. Solution: \(~17,491\)
43. 7610 people
47. 4,463 people
49. a. \(k≈0.0578,\) b. ≈ \(92\) hours
51. 15.66 yrs
53. Solution: a. \(~333\) million
\(quad\) b. 94 years from 2013, or in 210755. 34.66 yrs
D: Exponential Decay
Exercise \(\PageIndex{D}\)
Find current amount
61. Suppose that a certain radioactive isotope has an annual decay rate of 17.3%. Starting with a 214 gram sample, how many grams will be left after 5 years? Round your answer to the nearest hundredth.
62. Suppose that a certain radioactive isotope has an annual decay rate of 12.5%. Starting with a 127 gram sample, how many grams will be left after 6 years? Round your answer to the nearest hundredth.
Find original amount
63. Suppose that a certain radioactive isotope has an annual decay rate of 2.3%. If a particular sample decays to 25 grams after 8 years, how big (in grams) was the original sample? Round your answer to the nearest hundredth.
64. Suppose that a certain radioactive isotope has an annual decay rate of 9.8%. If a particular sample decays to 11 grams after 6 years, how big (in grams) was the original sample? Round your answer to the nearest hundredth.
Find decay rate
65. The half-life of Erbium-165 is \(10.4\) hours. What is the hourly decay rate? Express the decimal result to four significant digits and the percentage to two significant digits.
66. The half-life of Radium-226 is \(1590\) years. What is the annual decay rate? Express the decimal result to four significant digits and the percentage to two significant digits.
Find time (half life)
68. A doctor prescribes \(125\) milligrams of a therapeutic drug that has an hourly decay rate of about \(30\%\).
(a) Write an exponential model, \(f(t)\), representing the amount of the drug remaining in the patient’s system after \(t\) hours. Then use the formula to find the amount of the drug that would remain in the patient’s system after \(3\) hours. Round to the nearest tenth of a milligram.
(b) To the nearest tenth of an hour, what is the half-life of the drug?
(c) Using the model found in part (a), find \(f(10)\) and interpret the result. Round to the nearest hundredth.
69. A scientist begins with \(250\) grams of a radioactive substance. After \(225\) minutes, the sample has decayed to \(32\) grams. Rounding to five significant digits, write an exponential equation representing this situation. To the nearest minute, what is the half-life of this substance?
70. A substance has a half-life of \(2.045\) minutes. If the initial amount of the substance was \(132.8\) grams, how many half-lives will have passed before the substance decays to \(8.3\) grams? What is the total time of decay?
71. Suppose that a certain radioactive isotope has an annual decay rate of 17.4%. What is the half-life (in years) of the isotope? Round your answer to the nearest hundredth.
72. Suppose that a certain radioactive isotope has an annual decay rate of 5.2%. What is the half-life (in years) of the isotope? Round your answer to the nearest hundredth.
Find time
73. Suppose that a certain radioactive isotope has an annual decay rate of 7.2%. How many years will it take for a 227 gram sample to decay to 93 grams? Round your answer to the nearest hundredth.
74. A tumor is injected with \(0.5\) grams of Iodine-125, which has a decay rate of \(1.15\%\) per day.
(a) Write an exponential model representing the amount of Iodine-125 remaining in the tumor after \(t\) days. Then use the formula to find the amount of Iodine-125 that would remain in the tumor after \(30\) days. Round to the nearest hundredth of a gram.
(b) To the nearest day, how long will it take for half of the Iodine-125 to decay?
75. Suppose that a certain radioactive isotope has an annual decay rate of 18.7%. How many years will it take for a 324 gram sample to decay to 163 grams? Round your answer to the nearest hundredth.
76. Iodine-131 is a radioactive substance that decays according to the function \(Q(t)=Q_0⋅e^{−0.08664t}\), where \(Q_0\) is the initial quantity of a sample of the substance and t is in days. Determine how long it takes (to the nearest day) for 95% of a quantity to decay.
77. Suppose that 90.1% of the normal amount of carbon-14 remains in a piece of wood. How old is the wood? The decay rate of carbon-14 is 0.012%. Round your answer to the nearest year.
78. A wooden artifact from an archeological dig contains \(60\) percent of the carbon-14 that is present in living trees. To the nearest year, about how many years old is the artifact? (The half-life of carbon-14 is \(5730\) years.)
79. Suppose that only 6.2% of the normal amount of carbon-14 remains in a fragment of bone. How old is the bone? The decay rate of carbon-14 is 0.012%. Round your answer to the nearest year.
80. Suppose that 96.7% of the normal amount of carbon-14 remains in a piece of cloth. How old is the cloth? The decay rate of carbon-14 is 0.012%. Round your answer to the nearest year.
- Answers to odd exercises:
-
61. 90.11g
63. 30.05g
65. \(r \approx -0.0667\),
So hourly decay rate is \( \approx 6.67\%\)69. \(f(t)=250e^{(-0.00914t)}\);
half-life: about \(76\) minutes71. 3.98 yrs
73. 12.39 yrs
75. 3.67 yrs
77. 869 years
79. 23172 years
E: Exponential Growth and Decay
Exercise \(\PageIndex{E}\)
Find current amount
81. The population of a small town of \(24,000\) people is expected grow exponentially at a rate of \(1.6\)% per year. Construct an exponential growth model and use it to:
a. Estimate the population in \(3\) years’ time.
b. Estimate the time it will take for the population to reach \(30,000\) people.
82. During the exponential growth phase, certain bacteria can grow at a rate of \(4.1\)% per hour. If \(10,000\) cells are initially present in a sample, construct an exponential growth model and use it to:
a. Estimate the population in \(5\) hours.
b. Estimate the time it will take for the population to reach \(25,000\) cells.
83. In 2000, the world population was estimated to be \(6.115\) billion people and in 2010 the estimate was \(6.909\) billion people. If the world population continues to grow exponentially, estimate the total world population in 2020.
84. The population of the downtown area of a certain city decreased from \(12,500\) people to \(10,200\) people in two years. If the population continues to decrease exponentially at this rate, what would we expect the population to be in two more years?
85. Researchers recorded that a certain bacteria population declined from \(800,000\) to \(500,000\) in \(6\) hours after the administration of medication. At this rate of decay, how many bacteria will there be in \(24\) hours?
86. Researchers recorded that a certain bacteria population declined from \(100,000\) to \(100\) in \(24\) hours. At this rate of decay, how many bacteria will there be in \(16\) hours?
87. An automobile was purchased new for $\(42,500\) and \(2\) years later it was valued at $\(33,400\). Estimate the value of the automobile in \(5\) years if it continues to decrease exponentially.
88. A new MP3 player was purchased for $\(320\) and in \(1\) year it was selling used online for $\(210\). If the value continues to decrease exponentially at this rate, determine the value of the MP3 player \(3\) years after it was purchased.
89. A bacteria doubles its original population in \(24\) hours. How big will its population be in \(72\) hours?
90. A new PC was purchased for $\(1,200\) and in \(1.5\) years it was worth $\(520\). Assume the value is decreasing exponentially and estimate the value of the PC four years after it is purchased.
91. Radioactive technetium-99m is often used in diagnostic medicine as it has a relatively short half-life but lasts long enough to get the needed testing done on the patient. If its half-life is \(6\) hours, how much of the radioactive material form a \(0.5\) ml injection will be in the body in \(24\) hours?
92. Carbon-14 is used for archeological carbon dating. Its half-life is \(5,730\) years. How much of a \(100\)-gram sample of Carbon-14 will be left in \(1000\) years?
93. The half-life of caesium-137 is about \(30\) years. What percent of an initial sample will remain in \(100\) years?
94. The half-life of radioactive iodine-131 is about \(8\) days. What percent of an initial sample will remain in \(30\) days?
95. If a bone is \(100\) years old, what percent of its original amount of carbon-14 do we expect to find in it? (The half-life of carbon-14 is \(5730\) years.)
96. The half-life of plutonium-239 is about \(24,000\) years. What percent of an initial sample will remain in \(1,000\) years?
Find time
97. The half-life of radium-226 is about \(1,600\) years. How long will a \(5\)-milligram sample of radium-226 take to decay to \(1\) milligram?
98. The half-life of plutonium-239 is about \(24,000\) years. How long will a \(5\)-milligram sample of plutonium-239 take to decay to \(1\) milligram? 121. Find the amount of time it will take for \(10\)% of an initial sample of plutonium-239 to decay. (Hint: If \(10\)% decays, then \(90\)% will remain.)
99. The half-life of radioactive iodine-131 is about \(8\) days. How long will it take a \(28\)-gram initial sample of iodine-131 to decay to \(12\) grams?
100. The half-life of caesium-137 is about \(30\) years. How long will it take a \(15\)-milligram sample of caesium-137 to decay to \(5\) milligrams? 116. How long will it take a sample of caesium-137 to decay to \(25\)% of the original amount?
101. The Rhind Mathematical Papyrus is considered to be the best example of Egyptian mathematics found to date. This ancient papyrus was found to contain \(64\)% of the carbon-14 normally found in papyrus. Given that carbon-14 has a half-life of \(5,730\) years, estimate the age of the papyrus.
102. A wooden bowl artifact carved from oak was found to contain \(55\)% of the carbon-14 normally found in oak. Given that carbon-14 has a half-life of \(5,730\) years, estimate the age of the bowl.
103. The half-life of radioactive iodine-131 is about \(8\) days. How long will it take a sample of iodine-131 to decay to \(10\)% of the original amount?
104. A virus takes \(6\) days to double its original population. How long will it take to triple its population?
- Answers to odd exercises:
-
81. (a) About \(25,180 \) people
(b) About \(14\) years83. About \(7.806 \) billion people
85. \(122,070\) bacteria
87. About $\(23,269.27\)
89. \(8\) times as large as the original population
91. \(0.03\) mL
93. \(9.9 \%\)
95. \(98.8\%\)
97. \(3,715\) years
99. \(9.8\) days
101. About \(3,689\) years old
103. \(26.6\) days
F: Newton' s Law of Heating and Cooling
Exercise \(\PageIndex{F}\)
111. The temperature of an object in degrees Fahrenheit after \(t\) minutes is represented by the equation \(T(t)=68e^{-0.0174t}+72\) . To the nearest degree, what is the temperature of the object after one and a half hours?
112. A pot of boiling soup with an internal temperature of \(100^{\circ}\) Fahrenheit was taken off the stove to cool in a \(69^{\circ}\) F room. After fifteen minutes, the internal temperature of the soup was \(95^{\circ}\) F.
a) Use Newton’s Law of Cooling to write a formula that models this situation.
b) To the nearest minute, how long will it take the soup to cool to \(80^{\circ}\) F?
c) To the nearest degree, what will the temperature be after \(2\) and a half hours?
113. A turkey is taken out of the oven with an internal temperature of \(165^{\circ}\) F and is allowed to cool in a \(75^{\circ}\) F room. After half an hour, the internal temperature of the turkey is \(145^{\circ}\) F.
(a) Write a formula that models this situation.
(b) To the nearest degree, what will the temperature be after \(50\) minutes?
(c) To the nearest minute, how long will it take the turkey to cool to \(110^{\circ}\) F?
- Answers to odd exercises:
- 111. about \(86.2^{\circ} \) F 113. (a) \(T(t) = 90e^{(-0.008377t)}+75\), where \(t\) is in minutes. (b) \(134^\circ \) F (c) about \(113\) minutes
G: Logistic Growth
Exercise \(\PageIndex{G}\)
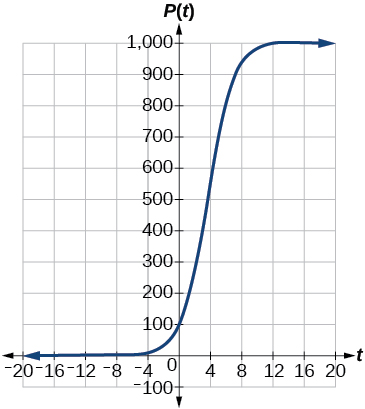 121. The population of a fish farm in \(t\) years is modeled by the equation \(P(t)=\dfrac{1000}{1+9e^{-0.6t}}\). The graph of the function is at the right.
121. The population of a fish farm in \(t\) years is modeled by the equation \(P(t)=\dfrac{1000}{1+9e^{-0.6t}}\). The graph of the function is at the right.
a) What is the initial population of fish?
b) To the nearest tenth, what is the doubling time for the fish population?
c) To the nearest whole number, what will the fish population be after \(2\) years?
d) To the nearest tenth, how long will it take for the population to reach \(900\)?
e) What is the carrying capacity for the fish population? Justify your answer using the graph of \(P\).
122. The equation \(N(t)=\dfrac{500}{1+49e^{-0.7t}}\) models the number of people in a town who have heard a rumor after \(t\) days.
a) How many people started the rumor?
b) To the nearest whole number, how many people will have heard the rumor after \(3\) days?
c) As \(t\) increases without bound, what value does \(N(t)\) approach? Interpret your answer.
123. What is the \(y\)-intercept of the logistic growth model \(y=\dfrac{c}{1+ae^{-rx}}\) ? Show the steps for calculation. What does this point tell us about the population?
124. A logistic model is given by the equation \(P(t)=\dfrac{90}{1+5e^{-0.42t}}\). To the nearest hundredth, for what value of \(t\) does \(P(t)=45\)
125. To the nearest whole number, what is the initial value of a population modeled by the logistic equation \(P(t)=\dfrac{175}{1+6.995e^{-0.68t}}\)? What is the carrying capacity?151) What is the \(y\)-intercept on the graph of the logistic model given in the previous exercise?
126. The number of cells in a certain bacteria sample is approximated by the logistic growth model \(N(t)=\frac{1.2 \times 10^{5}}{1+9 e^{-0.32t}}\), where \(t\) represents time in hours. Determine the time it takes the sample to grow to \(24,000\) cells.
127. Given the logistic growth model
a) Find and interpret \(f(0)\)Round to the nearest tenth.
b) Find and interpret \(f(4)\) . Round to the nearest tenth.
c) Find the carrying capacity.
128. The population \(P\) of an endangered species habitat for wolves is modeled by the function \(P(x)=\dfrac{558}{1+54.8e^{-0.462x}}\)where \(x\) is given in years.
a) What was the initial population of wolves transported to the habitat?
b) How many wolves will the habitat have after \(3\) years?
c) How many years will it take before there are \(100\) wolves in the habitat?
- Answers to odd exercises:
- 121. (a) 100 fish, (b) about \(1.4\) years, (c) \(269 \) fish, (d) about \(7.3\) years, (e) 1000 fish - the upper horizontal asymptote bound
123. \(\dfrac{c}{1+a}\); initial population size 125. \(P(0)=22\); \(175\)
127. (a) \(f(0)\approx 16.7\); The amount initially present is about \(16.7\) units. (b) The quantity after 4 hours is \(149.6 \) units (c) \(150\)
\( \star \)

