5.1e: Exercises - Angles
- Page ID
- 56286
A: Concepts
Exercise \(\PageIndex{A}\)
1) Draw an angle in standard position. Label the vertex, initial side, and terminal side.
2) Explain why there are an infinite number of angles that are coterminal to a certain angle.
3) State what a positive or negative angle signifies, and explain how to draw each.
4) How does radian measure of an angle compare to the degree measure? Include an explanation of \(1\) radian in your paragraph.
- Answers to odd exercises:
-
1.
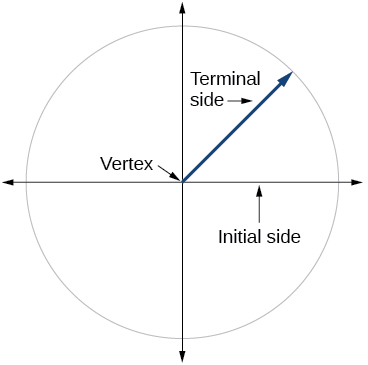
3. Whether the angle is positive or negative determines the direction. A positive angle is drawn in the counterclockwise direction, and a negative angle is drawn in the clockwise direction.
B: Draw Angles in Standard Position
Exercise \(\PageIndex{B}\)
\( \bigstar \) Draw an angle in standard position with the given measure. If the angle measure is not between \(0\) and \(2 \pi \) or between \(0^{\circ}\) and \(360^{\circ}\), also state the coterminal angle that is within that interval.
|
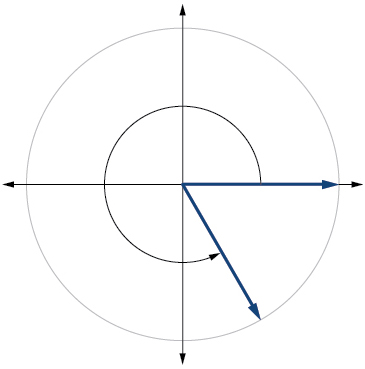
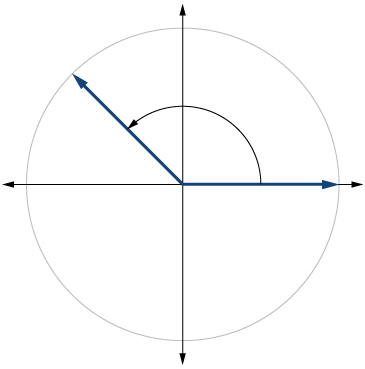
5. \(300^{\circ}\) 6. \(415^{\circ}\) 7. \(135^{\circ}\) 8. \(-30^{\circ}\) 9. \(-120^{\circ}\) 10. \(-315^{\circ}\) |
11. \(\dfrac{2π}{3}\) 12. \(\dfrac{5π}{3}\) 13. \(−\dfrac{4π}{3}\) 14. \(−\dfrac{5π}{3}\) |
15. \(\dfrac{5π}{6}\) 16. \(\dfrac{11π}{6}\) 17. \(−\dfrac{π}{6}\) 18. \(\dfrac{7π}{6}\) |
19. \( \dfrac{7π}{4}\) 20. \(\dfrac{5π}{4}\) 21. \(−\dfrac{3π}{4}\) 22. \(\dfrac{11π}{4}\) |
23. \(\dfrac{22π}{3}\) 24. \( \dfrac{17π}{6} \) 25. \(−\dfrac{π}{10}\) 26. \(\dfrac{23π}{5}\) |
27. \(\dfrac{π}{2}\) 28. \( -\dfrac{3π}{2}\) 29. \( \dfrac{7π}{2}\) 30. \( -5π \) |
- Answers to odd exercises:
-
5. 
7. 
9. \(240^{\circ}\) 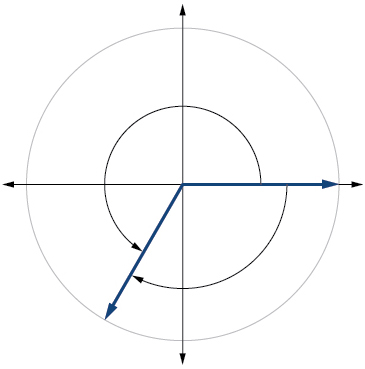
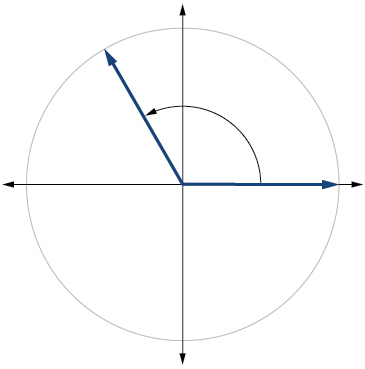
11. 
13. \(\frac{2π}{3}\) 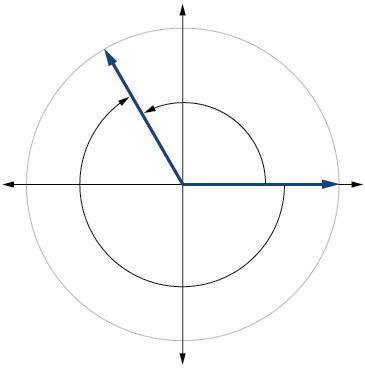 x
x 15.
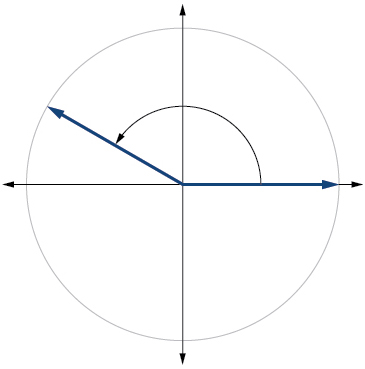
17.
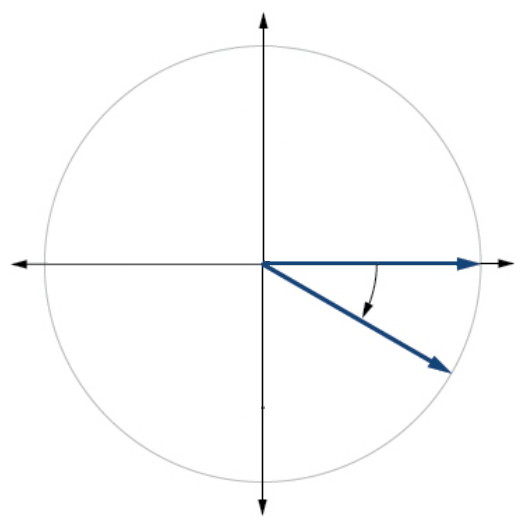
19.
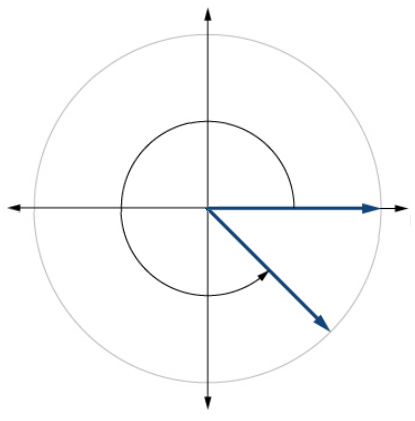
21.
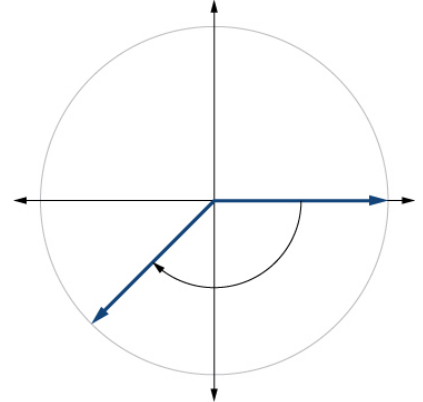
23. \(\frac{4π}{3}\)
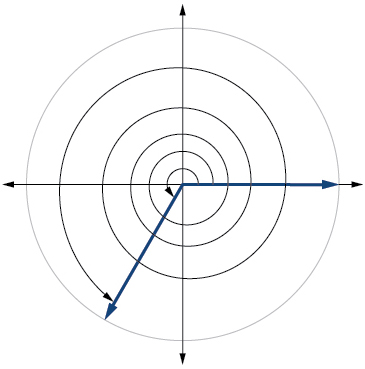
25. \(\frac{19π}{10}\)
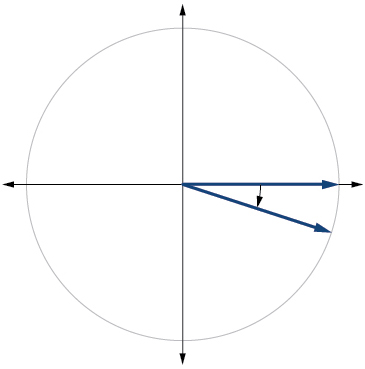
27.
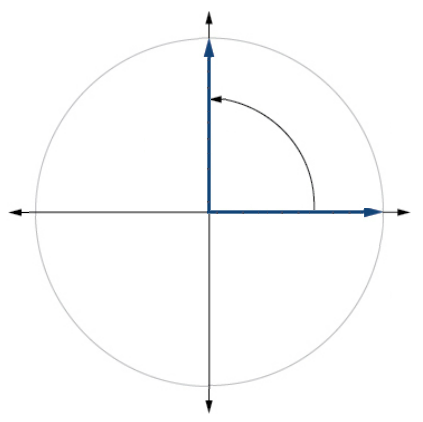
29 . \(\frac{3π}{2}\)
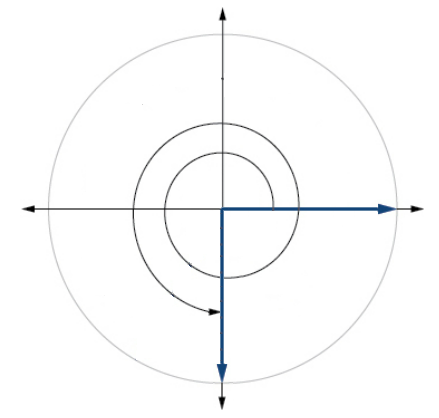
C: Convert between radians and degrees
Exercise \(\PageIndex{C}\)
\( \bigstar \) Convert angles in radians to degrees.
|
36. \(\dfrac{3π}{4}\) radians
37. \(\dfrac{π}{9}\) radians |
38. \(−\dfrac{5π}{4}\) radians
39. \(\dfrac{π}{3}\) radians |
40. \(−\dfrac{7π}{3}\) radians
41. \(−\dfrac{5π}{12}\) radians |
42. \(\dfrac{11π}{6}\) radians
|
\( \bigstar \) Convert angles in degrees to radians. Write the answer both as a multiple of pi and to the nearest hundredth of a radian.
| 43. \(90^{\circ}\) | 44. \(100^{\circ}\) | 45. \(-540^{\circ}\) | 46. \(-120^{\circ}\) | 47. \(180^{\circ}\) | 48. \(-315^{\circ}\) | 49. \(150^{\circ}\) |
- Answers to odd exercises:
-
37. \(20^{\circ} \qquad \) 39. \(60^{\circ} \qquad \) 41. \(-75^{\circ} \qquad \) 43. \(\frac{π}{2} \; \approx \; 1.57\) radians \( \qquad \) 45. \(−3π \; \approx \; 9.42\) radians
47. \(π \; \approx \; 3.14 \) radians \( \qquad \) 49. \(\frac{5π}{6} \; \approx \; 2.62\) radians
D: Coterminal Angles
Exercise \(\PageIndex{D}\)
\( \bigstar \) Find the angle between \(0^{\circ}\) and \(360^{\circ}\) that is coterminal to the given angle.
50. \(-40^{\circ}\) \( \qquad \) 51. \(-110^{\circ}\) \( \qquad \) 52. \(700^{\circ}\) \( \qquad \) 53. \(1400^{\circ}\)
\( \bigstar \) Find the angle between \(0\) and \(2\pi \) in radians that is coterminal to the given angle.
54. \(−\dfrac{π}{9}\) \( \qquad \) 55. \(\dfrac{10π}{3}\) \( \qquad \) 56. \(\dfrac{13π}{6}\) \( \qquad \) 57. \(\dfrac{44π}{9}\)
- Answers to odd exercises:
-
51. \(250^{\circ}\) \( \qquad \) 53. \(320^{\circ}\) \( \qquad \) 55. \(\frac{4π}{3}\) \( \qquad \) 57. \(\frac{8π}{9}\)

