5.3e: Exercises - Sine and Cosine Functions
- Page ID
- 69487
A: Concepts
Exercise \(\PageIndex{A}\)
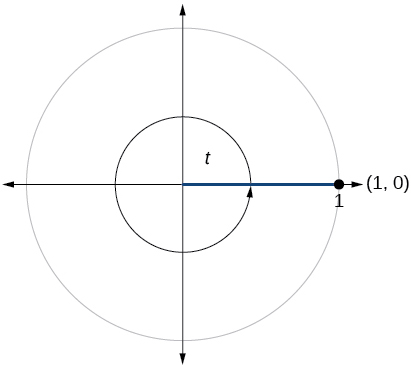
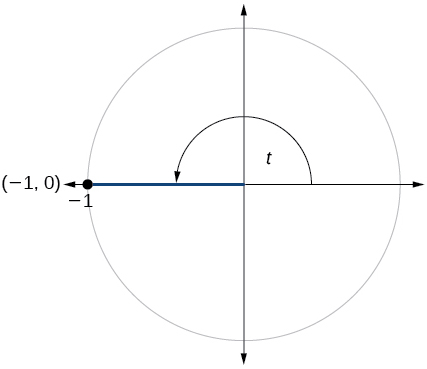
1) Describe the unit circle.
2) What do the \(x\)- and \(y\)-coordinates of the points on the unit circle represent?
3) Discuss the difference between a coterminal angle and a reference angle.
4) Explain how the cosine of an angle in the second quadrant differs from the cosine of its reference angle in the unit circle.
5) Explain how the sine of an angle in the second quadrant differs from the sine of its reference angle in the unit circle.
6) State the domain of the sine and cosine functions.
7) State the range of the sine and cosine functions.
- Answers to Odd Problems:
-
1. The unit circle is a circle of radius \(1\) centered at the origin.
3. Coterminal angles are angles that share the same terminal side. A reference angle is the size of the smallest acute angle, \(t\), formed by the terminal side of the angle \(t\) and the horizontal axis.
5. The sine values are equal.
7. \([–1,1]\)
B. Find sine or cosine values given a point on the terminal side of an angle or given a quadrantal angle
Exercise \(\PageIndex{B}\)
\( \bigstar \) Find the sine and cosine of an angle \( \theta \) that has the following point on its terminal side. Give exact answers.
11. \( (2, 3) \) \( \;\; \) 12. \( (11, 6) \) \( \;\; \) 13. \( (-4, 1) \) \( \;\; \) 14. \( (-2, 8) \) \( \;\; \) 15. \( (-3, -5) \) \( \;\; \) 16. \( (-10, -6) \) \( \;\; \) 17. \( (6, -17) \) \( \;\; \) 18. \( (9, -5) \)
\( \bigstar \) Find the sine and cosine of the following angles.
21. \(0^{\circ}\) \(\quad \) 22. \(900^{\circ}\) \(\quad \) 23. \(-90^{\circ}\) \(\quad \) 24. \(-630^{\circ}\) \(\quad \) 25. \( 7 \pi \) \(\quad \) 26. \( 4 \pi \) \(\quad \) 27. \( \dfrac{-7 \pi}{2} \) \(\quad \) 28. \( \dfrac{-13 \pi}{2} \)
- Answers to Odd Problems:
-
11. \( \sin \theta = \dfrac {3\sqrt{13}}{13}, \) \( \cos \theta = \dfrac {2\sqrt{13}}{13} \)
13. \( \sin \theta = \dfrac {\sqrt{17}}{17}, \) \( \cos \theta = \dfrac {-4\sqrt{17}}{17} \)15. \( \sin \theta = \dfrac {-5\sqrt{34}}{34}, \) \( \cos \theta = \dfrac {-3\sqrt{34}}{34} \)
17. \( \sin \theta = \dfrac {-17\sqrt{13}}{65}, \) \( \cos \theta = \dfrac {6\sqrt{13}}{65} \)21. \( \sin \theta = 0, \) \( \cos \theta = 1 \) \(\quad \)23. \( \sin \theta = -1, \) \( \cos \theta = 0 \) \(\quad \)25. \( \sin \theta = 0, \) \( \cos \theta = -1 \) \(\quad \)27. \( \sin \theta = 1, \) \( \cos \theta = 0 \)
C. Find the quadrant an angle is in from the signs of a sine and cosine function
Exercise \(\PageIndex{C}\)
\( \bigstar \) Use the given sign of the sine and cosine functions to find the quadrant in which the terminal point determined by \(t\) lies.
|
31. \( \sin (t)>0\) and \( \cos (t)>0\) 32. \( \sin (t)<0\) and \( \cos (t)<0\) |
33. \( \sin (t)<0 \) and \( \cos (t)>0\) 34. \( \sin (t)>0 \) and \( \cos (t)<0\) |
- Answers to Odd Problems:
-
31. \(\textrm{I}\) \(\qquad\) 33. \(\textrm{IV}\)
D. Find sine or cosine values given another trig ratio and the quadrant the angle is in
Exercise \(\PageIndex{D}\)
\( \bigstar \) Find \( \cos \theta \) given the following information.
|
41. \({\rm sin}\left(\theta \right)=\dfrac{3}{8}\) and \(\theta\) is in the 2\({}^{nd}\) quadrant. 42. \({\rm sin}\left(\theta \right)=-\dfrac{1}{4}\) and \(\theta\) is in the 3\({}^{rd}\) quadrant. 43. \( \sin \theta = -\dfrac{1}{3}\) and \( \dfrac{3\pi}{2} < \theta < 2\pi \) |
44. \( \sin \theta = -\dfrac{3}{4}\) and \( \pi < \theta < \dfrac{3\pi}{2} \) 45. \( \sin \theta = \dfrac{5}{7}\) and \( \cos \theta < 0 \) 46. \( \sin \theta = \dfrac{1}{3}\) and \( \cos \theta > 0 \) |
\( \bigstar \) Find \( \sin \theta \) given the following information.
|
51.\({\rm cos}\left(\theta \right)=\dfrac{1}{7}\) and \(\theta\) is in the 4\({}^{th}\) quadrant. 52. \({\rm cos}\left(\theta \right)=\dfrac{2}{9}\) and \(\theta\) is in the 1\({}^{st}\) quadrant. 53. \( \cos \theta = -\dfrac{3}{5}\) and \( \dfrac{\pi}{2} < \theta < \pi \) |
54. \( \cos \theta = -\dfrac{2}{3}\) and \(\pi< \theta < \dfrac{3\pi}{2} \) 55. \( \cos \theta = -\dfrac{1}{5}\) and \( \sin \theta < 0 \) 56. \( \cos \theta = \dfrac{5}{6}\) and \( \sin \theta < 0 \) |
- Answers to Odd Problems:
-
41. \(-\dfrac{\sqrt{55}}{8}\) \(\qquad\) 43. \(\dfrac{2\sqrt{2}}{3}\) \(\qquad\) 45. \(-\dfrac{2\sqrt{6}}{7}\) \(\qquad\) 51. \(-\dfrac{4\sqrt{3}}{7}\) \(\qquad\) 53. \(\dfrac{4}{5}\) \(\qquad\) 55. \(-\dfrac{2\sqrt{6}}{5}\)
E. Reference angles
Exercise \(\PageIndex{E}\)
\( \bigstar \) State the reference angle for the given angle.
|
71. \(135°\) 72. \(240°\) 73. \(100°\) |
74. \(−315°\) 75. \(−170°\) 76. \( −47°\) |
77. \(\dfrac{2π}{3}\) 78. \(\dfrac{5π}{4}\) |
79. \(\dfrac{11π}{6}\) 80. \(−\dfrac{11π}{3}\) |
81. \(\dfrac{29π}{6}\) 82. \(\dfrac{10π}{7}\) |
83. \(\dfrac{−3π}{8}\) 84. \(\dfrac{7π}{5}\) |
85. \( 1.33 \) 86. \( 1.98 \) 87. \( 4.19 \) |
88. \( -1.07 \) 89. \( 15.20 \) 90. \( -19.50 \) |
- Answers to Odd Problems:
-
71. \(45°\) \(\quad\) 73. \(80°\) \(\quad\) 75. \(10 °\) \(\quad\) 77. \(\dfrac{π}{3}\) \(\quad\) 79. \(\dfrac{π}{6}\) \(\quad\) 81. \(\dfrac{π}{6}\) \(\quad\) 83. \(\dfrac{3π}{8}\) \(\quad\) 85. \( 1.33\) \(\quad\) 87. \( 1.05\) \(\quad\) 89. \( 0.51\)
\( \bigstar \) Find an angle \( \theta \) with \(0^{\circ} <\theta <360^{\circ} \) or \(0<\theta <2\pi\) that has the same sine value as the following angles.
|
91. \(\dfrac{\pi }{3} \) |
92. \(\dfrac{\pi }{4}\) |
93. \(\dfrac{4\pi }{3}\) |
94. \(\dfrac{7\pi }{6}\) |
95. 80\(\mathrm{{}^\circ}\) 96. 15\(\mathrm{{}^\circ}\) |
97. 140\(\mathrm{{}^\circ}\) 98. 160\(\mathrm{{}^\circ}\) |
99. 305\(\mathrm{{}^\circ}\) 100. 340\(\mathrm{{}^\circ}\) |
\( \bigstar \) Find an angle \( \theta \) with \(0^{\circ} <\theta <360^{\circ} \) or \(0<\theta <2\pi\) that has the same cosine value as the following angles.
|
101. \(\dfrac{\pi }{3}\) |
102. \(\dfrac{\pi }{4}\) |
103. \(\dfrac{4\pi }{3}\) |
104. \(\dfrac{7\pi }{6}\) |
105. 80\(\mathrm{{}^\circ}\) 106. 15\(\mathrm{{}^\circ}\) |
107. 140\(\mathrm{{}^\circ}\) 108. 160\(\mathrm{{}^\circ}\) |
109. 305\(\mathrm{{}^\circ}\) 110. 340\(\mathrm{{}^\circ}\) |
- Answers to Odd Problems:
-
91. \(\dfrac{2\pi}{3} \) \(\qquad\) 93. \(\dfrac{5\pi}{3}\) \(\qquad\) 95. \(100^{\circ} \) \(\qquad\) 97. \(40^{\circ}\) \(\qquad\) 99. \(235^{\circ}\)
101. \(\dfrac{5\pi}{3}\) \(\qquad\) 103. \(\dfrac{2\pi}{3}\) \(\qquad\) 105. \(280^{\circ}\) \(\qquad\) 107. \(220^{\circ}\) \(\qquad\) 109. \(55^{\circ}\)
\( \bigstar \) Find the reference angle, the quadrant of the terminal side, and the sine and cosine of each angle.
|
111. \(300° \\[4pt] \) 112. \(320°\) |
113. \(135°\\[4pt] \) 114. \(225°\) |
115. \(120°\\[4pt] \) 116. \(250°\) |
117. \(150°\\[4pt] \) 118. \(210°\) |
119. \(\dfrac{7π}{6}\) 120. \(\dfrac{5π}{3}\) |
121. \(\dfrac{3π}{4}\) 122. \(\dfrac{5π}{4}\) |
123. \(\dfrac{2π}{3}\) 124. \(\dfrac{5π}{6}\) |
125. \(\dfrac{7π}{4}\) 126. \(\dfrac{4π}{3}\) |
- Answers to Odd Problems:
-
111. \(60°\), QIV, \( \sin (300°)=−\dfrac{\sqrt{3}}{2},\; \cos (300°)=\dfrac{1}{2}\)
113. \(45°\), QII, \( \sin (135°)=\dfrac{\sqrt{2}}{2},\; \cos (135°)=−\dfrac{\sqrt{2}}{2}\)
115. \(60°\), QII, \(\sin (120°)=\dfrac{\sqrt{3}}{2}\), \(\cos (120°)=−\dfrac{1}{2}\)
117. \(30°\), QII, \( \sin (150°)=\frac{1}{2}\), \(\cos(150°)=−\dfrac{\sqrt{3}}{2}\)119. \(\dfrac{π}{6}\), QIII, \(\sin \left( \dfrac{7π}{6}\right )=−\dfrac{1}{2}\), \(\cos \left (\dfrac{7π}{6} \right)=−\dfrac{\sqrt{3}}{2}\)
121. \(\dfrac{π}{4}\), QII, \(\sin \left(\dfrac{3π}{4}\right)=\dfrac{\sqrt{2}}{2}\), \(\cos\left(\dfrac{4π}{3}\right)=−\dfrac{\sqrt{2}}{2}\)
123. \(\dfrac{π}{3}\), QII, \( \sin \left(\dfrac{2π}{3}\right)=\dfrac{\sqrt{3}}{2}\), \( \cos \left(\dfrac{2π}{3}\right)=−\dfrac{1}{2}\)
125. \(\dfrac{π}{4}\), QIV, \( \sin \left(\dfrac{7π}{4}\right)=−\dfrac{\sqrt{2}}{2}\), \( \cos \left(\dfrac{7π}{4}\right)=\dfrac{\sqrt{2}}{2}\)
F. Find sine or cosine for special angles
Exercise \(\PageIndex{F}\)
\( \bigstar \) Find the exact value of each trigonometric function.
|
131. \(\sin \dfrac{π}{3}\) 132. \( \sin \dfrac{π}{4}\) |
133. \( \sin \dfrac{π}{6}\) 134. \(\sin \dfrac{π}{2}\) |
135. \( \sin π\) 136. \( \sin \dfrac{3π}{2}\) |
137. \( \cos \dfrac{π}{3}\) 138. \( \cos \dfrac{π}{6}\) |
139. \( \cos \dfrac{π}{4}\) 140. \( \cos 0\) |
141. \( \cos π\) 142. \( \cos \dfrac{π}{2}\) |
- Answers to Odd Problems:
-
131. \(\dfrac{\sqrt{3}}{2}\) \(\qquad\) 133. \(\dfrac{1}{2}\) \(\qquad\) 135. \(0\) \(\qquad\) 137. \(\dfrac{1}{2}\) \(\qquad\) 139. \(\dfrac{\sqrt{2}}{2}\) \(\qquad\) 141. \(−1\)
\( \bigstar \) Evaluate. Give an exact answer. Do not use a calculator.
|
143. \( \sin \left(\dfrac{11π}{3}\right) \) 144. \( \sin \left(− \dfrac{4π}{3}\right) \) 145. \( \sin \left(\dfrac{−11π}{4}\right) \) |
146, \( \sin \left(\dfrac{−5π}{4}\right) \) 147. \( \sin \left(\dfrac{π}{6}\right) \) 148. \( \sin \left(\dfrac{11π}{6}\right)\) |
149. \( \cos \left(\dfrac{3π}{4}\right) \) 150. \( \cos \left(\dfrac{-π}{4}\right)\) 151. \( \cos \left(\dfrac{−2π}{3}\right) \) |
152. \( \cos \left(\dfrac{−4π}{3}\right) \) 153. \( \cos \left(\dfrac{−5π}{6}\right)\) 154. \( \cos \left(\dfrac{−π}{6}\right)\) |
155. \( \cos \left(\dfrac{-11π}{2}\right) \) 156. \( \sin 7\pi \) |
\( \bigstar \) Give exact values for \({\rm sin}\left(\theta \right)\) and \({\rm cos}\left(\theta \right)\) for each of these angles.
| 157. \(-\dfrac{3\pi }{4}\) | 158. \(\dfrac{23\pi }{6}\) | 159. \(-\dfrac{\pi }{2}\) | 150. \(5\pi\) | 161. 315\(\mathrm{{}^\circ}\) |
- Answers to Odd Problems:
-
143. \(-\frac{\sqrt{3}}{2}\) \(\qquad\) 145. \(−\frac{\sqrt{2}}{2}\) \(\qquad\) 147. \(\frac{1}{2}\) \(\qquad\) 149. \(−\frac{\sqrt{2}}{2}\) \(\qquad\) 151. \(-\frac{1}{2}\) \(\qquad\) 153. \(-\frac{\sqrt{3}}{2}\) \(\qquad\) 155. \(0\)
157. sin(\(-\frac{3\pi}{4}\)) = \(-\frac{\sqrt{2}}{2},\) cos(\(-\frac{3\pi}{4}\)) = \(-\frac{\sqrt{2}}{2}\) \( \qquad \) 159. sin(\(-\frac{\pi}{2}\)) = -1, cos(\(-\frac{\pi}{2}\)) = 0
161. sin( \( 315^{\circ} \) ) = \(-\frac{\sqrt{2}}{2},\) cos(\( 315^{\circ} \)) = \(\frac{\sqrt{2}}{2}\)
G. Find sine or cosine values using a calculator
Exercise \(\PageIndex{G}\)
\( \bigstar \) Use a calculator to evaluate.
|
171. \( \cos \dfrac{5π}{9}\) |
172. \( \sin \dfrac{5π}{9}\) |
173. \( \sin \dfrac{π}{10}\) |
174. \( \cos \dfrac{π}{10}\) |
175. \( \cos \dfrac{3π}{4}\) |
176. \(\sin \dfrac{3π}{4}\) |
| 177. \( \sin 310° \) | 178. \( \cos 310° \) | 179. \( \cos 98° \) | 180. \( \sin 98° \) |
- Answers to Odd Problems:
-
171. \(−0.1736\) \(\qquad\) 173. \(0.3090\) \(\qquad\) 175. \(−0.7071\) \(\qquad\) 177. \(−0.7660\) \(\qquad\) 179. \(−0.1392\)
H. Find points on a circle intersected by given angle
Exercise \(\PageIndex{H}\)
\( \bigstar \) Find exact values if possible, otherwise give answers to three decimal places.
182. Find the coordinates of the point on a circle with radius \(15\) corresponding to an angle of \(220°\).
183. Find the coordinates of the point on a circle with radius \(20\) corresponding to an angle of \(120°\).
184. Find the coordinates of the point on a circle with radius 20 corresponding to an angle of 280\(\mathrm{{}^\circ}\).
185. Find the coordinates of the point on a circle with radius \(16\) corresponding to an angle of \(\dfrac{5π}{9}\).
186. Find the coordinates of the point on a circle with radius \(8\) corresponding to an angle of \(\dfrac{7π}{4}\).
187. The point \(P\) is on the unit circle. If the \(y\)-coordinate of \(P\) is \(\dfrac{3}{5}\), and \(P\) is in quadrant II, find the \(x\) coordinate.
188. The point \(P\) is on the unit circle. If the \(x\)-coordinate of \(P\) is \(\dfrac{1}{5}\), and \(P\) is in quadrant IV, find the \(y\) coordinate.
- Answers to Odd Problems:
-
183. \((−10,10\sqrt{3})\) \(\qquad\) 185. \((–2.778,15.757)\) \(\qquad\) 187. \(-\dfrac{4}{5}\)
I: Applications
Exercise \(\PageIndex{I}\)
\( \bigstar \) For the exercises below, use this scenario: A child enters a carousel that takes one minute to revolve once around. The child enters at the point \((0,1)\), that is, on the due north position. Assume the carousel revolves counter clockwise.
190. What are the coordinates of the child after \(45\) seconds?
191. What are the coordinates of the child after \(90\) seconds?
192. What is the coordinates of the child after \(125\) seconds?
193. When will the child have coordinates \((0.707,–0.707)\) if the ride lasts \(6\) minutes? (There are multiple answers.)
194. When will the child have coordinates \((−0.866,−0.5)\) if the ride last \(6\) minutes?
196. Marla is running clockwise around a circular track. She runs at a constant speed of 3 meters per second. She takes 46 seconds to complete one lap of the track. From her starting point, it takes her 12 seconds to reach the northernmost point of the track. Impose a coordinate system with the center of the track at the origin, and the northernmost point on the positive \(y\)-axis.
a. Give Marla’s coordinates at her starting point.
b. Give Marla’s coordinates when she has been running for 10 seconds.
c. Give Marla’s coordinates when she has been running for 901.3 seconds.
- Answers to Odd Problems:
-
191. \((0,–1)\) \(\qquad\) 193. \(37.5\) seconds, \(97.5\) seconds, \(157.5\) seconds, \(217.5\) seconds, \(277.5\) seconds, \(337.5\) seconds
J: Using the Unit Circle
Exercise \(\PageIndex{J}\)
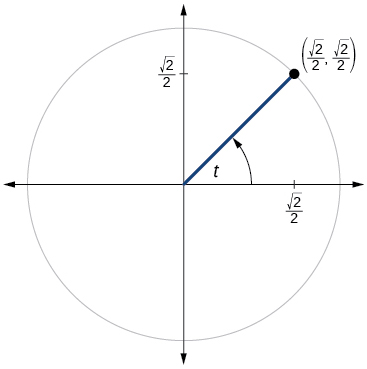
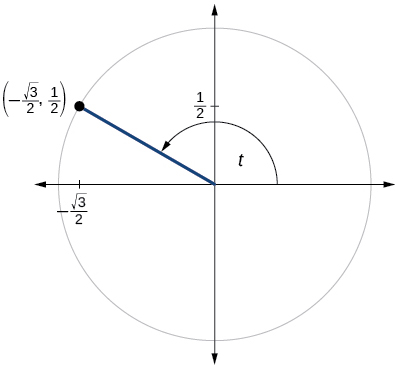
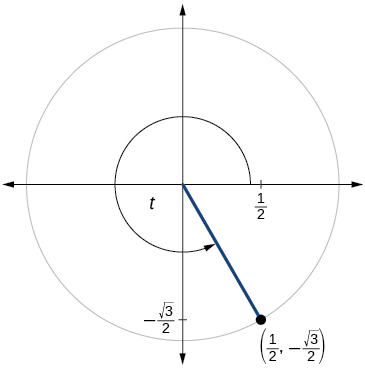
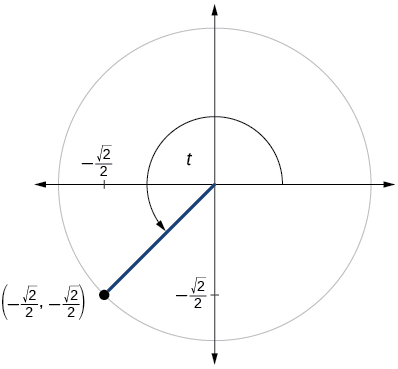
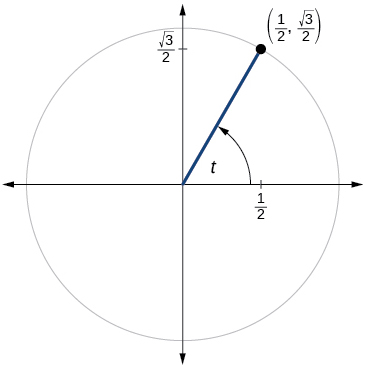
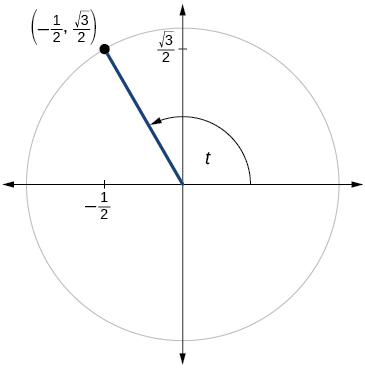
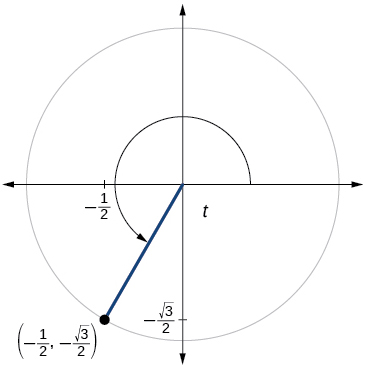
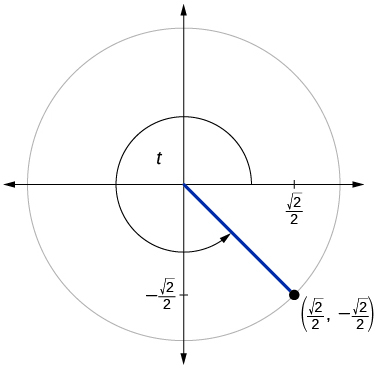
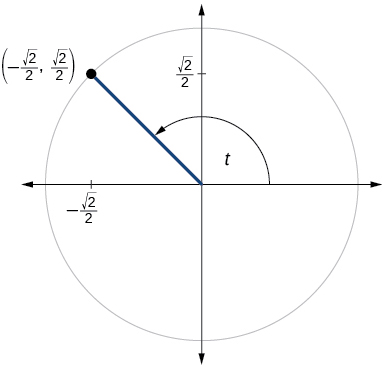
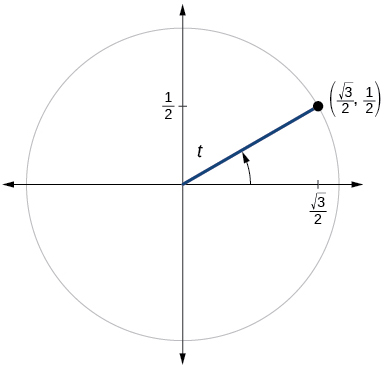
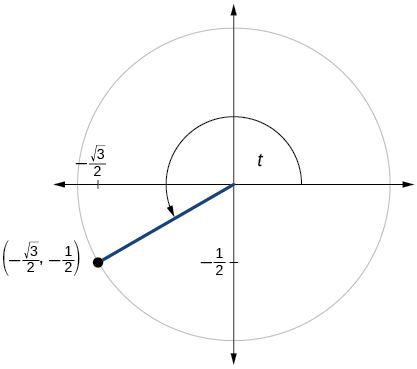
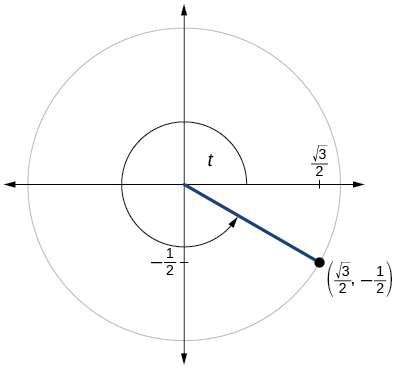
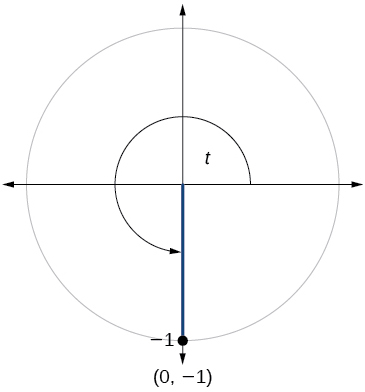
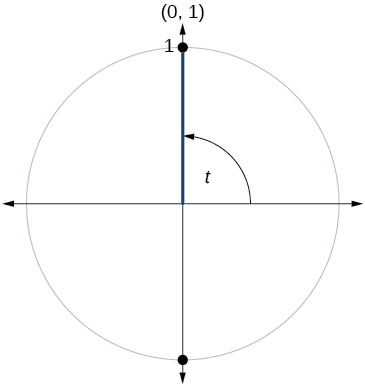
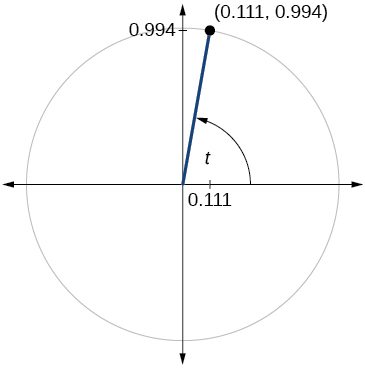
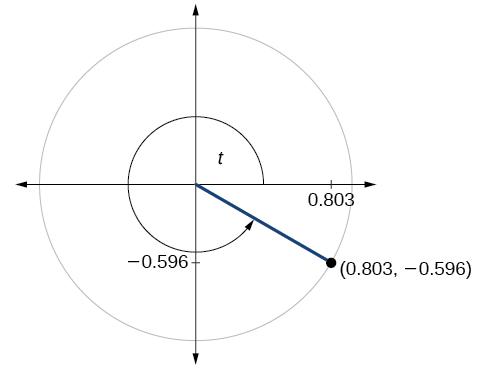
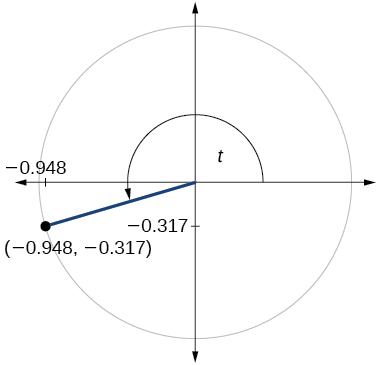
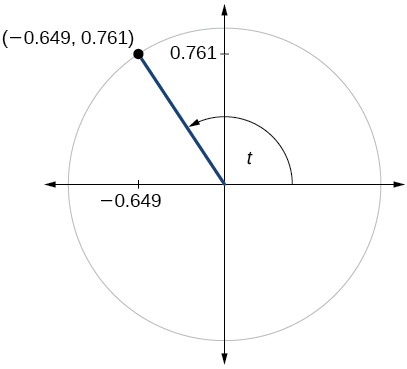
\( \bigstar \) For the exercises below, use the given point on the unit circle to find the value of the sine and cosine of \(t\).
|
200)
|
201)
|
202)
|
|
203)
|
204)
|
205)
|
|
206)
|
207)
|
208)
|
|
209)
|
210)
|
211)
|
|
212)
|
213)
|
214)
|
|
215)
|
216)
|
217)
|
|
218)
|
219)
|
|
- Answers to Odd Problems:
-
201. \( \sin t=\dfrac{1}{2}, \cos t=−\dfrac{\sqrt{3}}{2}\)
203. \( \sin t=− \dfrac{\sqrt{2}}{2}, \cos t=−\dfrac{\sqrt{2}}{2}\)
205. \( \sin t=\dfrac{\sqrt{3}}{2},\cos t=−\dfrac{1}{2}\)207. \( \sin t=− \dfrac{\sqrt{2}}{2}, \cos t=\dfrac{\sqrt{2}}{2}\)
209. \( \sin t=0, \cos t=−1\)
211. \(\sin t=\dfrac{1}{2}, \cos t= \dfrac{\sqrt{3}}{2}\)213. \( \sin t=−\dfrac{1}{2}, \cos t= \dfrac{\sqrt{3}}{2} \)
215. \( \sin t=1, \cos t=0\)
217. \( \sin t=−0.596, \cos t=0.803\)
219. \( \sin t=0.761, \cos t=−0.649 \)
\( \star \)