6.5e: Exercises: Double Angle, Half Angle and Reductions Formulas

Last updated
Save as PDF

Page ID: 74636

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

A: Concepts.

Exercise $\PageIndex{A}$

1) Explain how to determine the reduction identities from the double-angle identity $\cos(2x)=\cos^2x-\sin^2x$

2) Explain how to determine the double-angle formula for $\tan(2x)$ using the double-angle formulas for $\cos(2x)$ and $\sin (2x)$.

3) We can determine the half-angle formula for $\tan \left ( \dfrac{x}{2} \right )=\dfrac{\sqrt{1-\cos x}}{\sqrt{1+\cos x}}$ by dividing the formula for $\sin \left ( \dfrac{x}{2} \right )$ by $\cos \left ( \dfrac{x}{2} \right )$. Explain how to determine two formulas for $\tan \left ( \dfrac{x}{2} \right )$ that do not involve any square roots.

4) For the half-angle formula given in the previous exercise for $\tan \left ( \dfrac{x}{2} \right )$ , explain why dividing by $0$ is not a concern. (Hint: examine the values of $\cos x$ necessary for the denominator to be $0$.)

Answers to odd exercises.

1. Use the Pythagorean identities and isolate the squared term.

3. $\dfrac{1-\cos x}{\sin x}$, $\dfrac{\sin x}{1+\cos x}$, multiplying the top and bottom by $\sqrt{1-\cos x}$ and $\sqrt{1+\cos x}$, respectively.

B: Evaluate Double Angle Trigonometric Expressions

Exercise $\PageIndex{B}$

5. If $\sin x =\dfrac{1}{8}$ and $x$ is in quadrant $\mathrm{I} \\[4pt]$.

6. If $\sin x =\dfrac{2}{3}$, and $x$ is in quadrant $\mathrm{II} \\[4pt] $.

7. If $\cos x =-\dfrac{1}{2}$, and $x$ is in quadrant $\mathrm{III} $.

8. If $\cos x = \dfrac{5}{12} $, and $x$ is in quadrant $\mathrm{I}$.

9. If $\tan x = \dfrac{12}{5}$, and $x$ is in quadrant $\mathrm{I} \\[4pt] $.

10. If $\tan x =-8$, and $x$ is in quadrant $\mathrm{IV} \\[4pt] $.

$ \bigstar $ Find the values of the six trigonometric functions for angle $\theta$ if the conditions provided hold.

11. $\cos(2\theta )=\dfrac{3}{5}$ and $ \frac{\pi}{2} \leq \theta \leq \pi$

12. $\cos(2\theta )=\dfrac{1}{\sqrt{2}}$ and $ \pi \leq \theta \leq \frac{3\pi}{2} $

Answers to odd exercises.

5a. $\dfrac{3\sqrt{7}}{32}$ 5b. $\dfrac{31}{32}$ 5c. $\dfrac{3\sqrt{7}}{31}$ 7a. $\dfrac{\sqrt{3}}{2}$ 7b. $-\dfrac{1}{2}$ 7c. $-\sqrt{3}$ 9a. $\dfrac{120}{169},$ 9b. $ -\dfrac{119}{169}, $ 9c. $-\dfrac{120}{119}$

11. $\cos \theta =-\dfrac{2\sqrt{5}}{5},\sin \theta =\dfrac{\sqrt{5}}{5},\tan \theta =-\dfrac{1}{2},\csc \theta =\sqrt{5},\sec \theta =-\dfrac{\sqrt{5}}{2},\cot \theta =-2$

C: Use Double Angle Formulas to Solve Equations

Exercise $\PageIndex{C}$

$ \bigstar $ Use double angle formulas to solve exactly (where possible) on the interval $[0,2\pi )$.

20. $\sin(2t)=\cos t \\[2pt]$

21. $ \sin(2t)+ \sin t=0 \\[2pt]$

22. $\sin(2x)-\sin x=0 \\[2pt] $

23. $ \sin (2t) +3\cos (t) =0 \\[2pt]$

24. $\sin (4x)-\sin (2x)=0 $

25. $\dfrac{\sin (2x)}{\sec ^2 x}=0 \\[4pt] $

26. $\dfrac{\sin (2x)}{2\csc ^2 x}=0 \\[4pt] $

27. $\cos(2t)=\sin t \\[2pt]$

28. $\cos(6x)-\cos(3x)=0 $

29. $9\cos(2\theta )=9\cos^2\theta -4 \\[2pt]$

30. $3\cos (2\alpha )=2\cos ^{2} (\alpha ) $

31. $\cos(2x)-\cos x=0 $

32. $4\sin^2 x+\sin(2x)\sec x-3=0 $

33. $\sin^2 x-1+2\cos(2x)-\cos^2 x=1 $

34. $8\cos \left(2\alpha \right)=8\cos ^{2} \left(\alpha \right)-1$

35. $6\sin \left(2t\right)+9\sin \left(t\right)=0$

Answers to odd exercises.: 21. $ 0, \dfrac{2\pi }{3}, \pi , \dfrac{4\pi }{3} $ 23. $ \dfrac{\pi }{2}, \dfrac{3\pi }{2}$ 25. $0, \pi $ 27. $\dfrac{3\pi }{2}, \dfrac{\pi }{6}, \dfrac{5\pi }{6}$
29. $ 0.7297, \; 2.4119, \; 3.8713, \; 5.5535 $ 31. $0, \dfrac{2\pi }{3}, \dfrac{4\pi }{3}$ 33. No solution. 35. $ 0, \; \pi, \; 2.4189, \; 3.8643 $

D: Recognize patterns

Exercise $\PageIndex{D}$

$ \bigstar $ Simplify to one trigonometric expression. Do not evaluate.

41. $2\sin \left ( \dfrac{\pi }{4} \right )2\cos \left ( \dfrac{\pi }{4} \right )\\[4pt]$

42. $4\sin \left ( \dfrac{\pi }{8} \right )\cos \left ( \dfrac{\pi }{8} \right )\\[4pt]$

43. $6\sin (5x)\cos (5x) \\[4pt]$

44. $4\sin (8x)\cos (8x) \\[4pt]$

45. $\cos ^{2} \left(6x\right)-\sin ^{2} (6x)$

46. $\cos ^2(28^{\circ})-\sin ^2(28^{\circ}) \\[4pt]$

47. $2\cos ^2(37^{\circ})-1 \\[4pt]$

48. $1-2\sin ^2(17^{\circ})$

49. $\cos ^2(9x)-\sin ^2(9x) \\[4pt]$

50. $\cos ^{2} \left(37{}^\circ \right)-\sin ^{2} (37{}^\circ ) \\[4pt]$

Answers to odd exercises.: 41. $2\sin \left ( \dfrac{\pi }{2} \right )$ 43. $3\sin (10x)$ 45. $\cos ( 12x )$ 47. $\cos (74^{\circ})$ 49. $\cos (18x)$

E: Verify identities

Exercise $\PageIndex{E}$

$ \bigstar $ Prove the identity.

51. $(\sin^2x-1)^2=\cos(2x)+\sin^4x \\[4pt]$

52. $(\sin t-\cos t)^2=1-\sin(2t) \\[4pt]$

53. $\sin(2x)=-2 \sin(-x) \cos(-x) \\[4pt]$

54. $\cot x-\tan x=2 \cot(2x) \\[4pt]$

55. $\dfrac{1+\cos (2\theta )}{\sin (2\theta )}\tan ^2\theta =\tan \theta \\[4pt]$

56. $\dfrac{1+\cos (2t)}{\sin (2t)-\cos t}=\dfrac{2\cos t}{2\sin t-1} $

57. $\sin (2x)=\dfrac{2\tan x}{1+\tan ^2x} \\[4pt]$

58. $\cos (2\alpha )=\dfrac{1-\tan ^2\alpha }{1+\tan ^2\alpha } \\[4pt] \\[4pt]$

59. $\tan (2x)=\dfrac{2\sin x \cos x }{2\cos ^2 x-1}$

60. $\dfrac{\sin \left(2\theta \right)}{1+\cos \left(2\theta \right)} =\tan \left(\theta \right)$

61. $\cos(16x) = \Big( \cos^2(4x)-\sin^2(4x)-\sin(8x) \Big) \\ $
$ \cdot \; \Big( \cos^2(4x)-\sin^2(4x) + \sin(8x) \Big) $

62. $\sin(16x)=16 \sin x \cos x \cos(2x)\cos(4x)\cos(8x) \\[4pt]$

Answers to odd exercises.

51. $(\sin^2x-1)^2 = \sin^4 x - 2 \sin^2 x + 1 = \cos(2x)+\sin^4x $

53. $-2 \sin(-x)\cos(-x)=-2(-\sin(x)\cos(x))=\sin(2x)$

55. $\dfrac{\sin (2\theta )}{1+\cos (2\theta )}\tan ^2\theta =\dfrac{2\sin (\theta )\cos (\theta )}{1+\cos ^2\theta -\sin ^2\theta }\tan ^2\theta=\dfrac{2\sin (\theta )\cos (\theta )}{2\cos ^2\theta }\tan ^2\theta=\dfrac{\sin (\theta )}{\cos (\theta )}\tan ^2\theta \\
=\cot (\theta )\tan ^2\theta=\tan \theta$

57. $\dfrac{2\tan x}{1+\tan ^2x}=\dfrac{\tfrac{2\sin x}{\cos x}}{1+\tfrac{\sin ^2x}{\cos ^2x}}=\dfrac{\tfrac{2\sin x}{\cos x}}{\tfrac{\cos ^2x+\sin ^2x}{\cos ^2x}}=\dfrac{2\sin x}{\cos x}\cdot \dfrac{\cos ^2x}{1}=2\sin x \cos x=\sin (2x)$

59. $\dfrac{2\sin x \cos x }{2\cos ^2 x-1}=\dfrac{\sin (2x)}{ \cos (2x)}=\tan (2x)$

61. $ (\cos^2(4x)-\sin^2(4x)-\sin(8x))(\cos^2(4x)-\sin^2(4x)+\sin(8x)) \\
= (\cos(8x)-\sin(8x))(\cos(8x)+\sin(8x)) = \cos ^2 (8x)-\sin ^2 (8x)= \cos(16x) $

F: Use Power Reduction Formulas

Exercise $\PageIndex{F}$

$ \bigstar $ Rewrite the expression with an exponent no higher than 1.

70. $\cos ^2 (5x) \\[4pt]$

71. $\cos ^2 (6x) \\[4pt]$

72. $\sin ^4 (8x) \\[4pt]$

73. $\sin ^4 (3x)$

74. $\sin^2(2x) \\[4pt]$

75. $\sin^2x \cos^2x \\[4pt]$

76. $\tan^2x \sin^2x \\[4pt]$

77. $\tan^4x$

78. $\cos^2x \sin (2x) \\[4pt]$

79. $\tan^4x \cos^2 x \\[4pt] $

80. $\tan ^2\left ( \dfrac{x}{2} \right )\sin x \\[4pt]$

81. $\cos^2(2x) \sin x $

82. $\tan^2x \sin x \\[4pt]$

83. $\cos^4x \sin^2x \\[4pt]$

84. $\cos^2x \sin^4x \\[4pt]$

$ \bigstar $ Algebraically find an equivalent function, in terms of only $\sin x$ and/or $\cos x$

85. $\sin (4x)$

86. $\cos (4x)$

Answers to odd exercises.: 71. $\dfrac{1+\cos (12x)}{2}$ 73. $\dfrac{3+\cos(12x)-4\cos(6x)}{8}$ 75. $\dfrac{1-\cos(4x)}{8}$
77. $\dfrac{3+\cos(4x)-4\cos(2x)}{3+\cos(4x)+4\cos(2x)}$ 79. $\dfrac{3+\cos(4x)-4\cos(2x)}{4(\cos(2x)+1)}$ 81. $\dfrac{(1+\cos(4x))\sin x}{2}$
83. $\dfrac{2+\cos(2x)-2\cos(4x)-\cos(6x)}{32}$ 85. $4\sin x\cos x(\cos^2x-\sin^2x)$

G: Use Half Angle Formulas

Exercise $\PageIndex{G}$

$ \bigstar $ Find the exact value using half-angle formulas.

91. $\sin \left ( \dfrac{\pi }{8} \right ) \\[4pt]$

92. $\cos \left ( -\dfrac{11\pi }{12} \right )$

93. $\sin \left ( \dfrac{11\pi }{12} \right ) \\[4pt]$

94. $\cos \left ( \dfrac{7\pi }{8} \right )$

95. $\tan \left ( \dfrac{5\pi }{12} \right ) \\[4pt]$

96. $\tan \left ( -\dfrac{3\pi }{12} \right )$

97. $\tan \left ( -\dfrac{3\pi }{8} \right ) \\[4pt]$

$ \bigstar $ Find the exact values of a) $\sin \left ( \dfrac{x}{2} \right )$ b) $\cos \left ( \dfrac{x}{2} \right )$ and c) $\tan \left ( \dfrac{x}{2} \right )$ when $0 \leq \theta \leq 2\pi $

101. If $\sin x =-\dfrac{12}{13}$, and $x$ is in quadrant $\mathrm{III} \\[4pt] $.

102. If $\tan x =-\dfrac{4}{3}$, and $x$ is in quadrant $\mathrm{IV} $.

103. If $\sec x =-4$, and $x$ is in quadrant $\mathrm{II} \\[4pt] $.

104. If $\csc x =7$, and $x$ is in quadrant $\mathrm{II} $.

$ \bigstar $ Use the figure below to find the requested half angle trigonometric expressions.

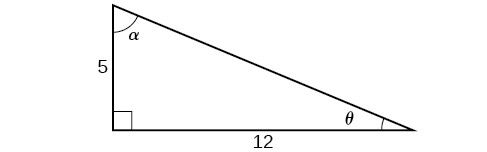
$CNX_Precalc_Figure_07_03_201.jpg$

107. Find $\sin \left (\dfrac{\alpha }{2} \right )$, $\cos \left (\dfrac{\alpha }{2} \right )$, and $\tan \left (\dfrac{\alpha }{2} \right )$.

108. Find $\sin \left (\dfrac{\theta }{2} \right )$, $\cos \left (\dfrac{\theta }{2} \right )$, and $\tan \left (\dfrac{\theta }{2} \right )\\[4pt]$.

Answers to odd exercises.

91. $\dfrac{\sqrt{2-\sqrt{2}}}{2}$ 93. $\dfrac{\sqrt{2-\sqrt{3}}}{2}$ 95. $2+\sqrt{3}$ 97. $-1-\sqrt{2}$

101a. $\dfrac{3\sqrt{13}}{13}$ 101b. $-\dfrac{2\sqrt{13}}{13}$ 101c. $-\dfrac{3}{2}$ 103a. $\dfrac{\sqrt{10}}{4}$ 103b. $\dfrac{\sqrt{6}}{4}$ 103c. $\dfrac{\sqrt{15}}{3}$

107. $\dfrac{2\sqrt{13}}{13}, \dfrac{3\sqrt{13}}{13}, \dfrac{2}{3}$

$ \bigstar $