2.7E: Precise Definition of Limit EXERCISES
- Page ID
- 10231
2.7: The Precise Definition of a Limit
In the following exercises, write the appropriate \(ε−δ\) definition for each of the given statements.
176) \(\displaystyle \lim_{x→a}\,f(x)=N\)
177) \(\displaystyle \lim_{t→b}\,g(t)=M\)
- Answer:
- For every \(ε>0\), there exists a \(δ>0\), so that if \(0<|t−b|<δ\), then \(|g(t)−M|<ε\)
178) \(\displaystyle \lim_{x→c}\,h(x)=L\)
179) \(\displaystyle \lim_{x→a}\,φ(x)=A\)
- Answer:
- For every \(ε>0\), there exists a \(δ>0\), so that if \(0<|x−a|<δ\), then \(|φ(x)−A|<ε\)
The following graph of the function f satisfies \(\displaystyle \lim_{x→2}f(x)=2\). In the following exercises, determine a value of \(δ>0\) that satisfies each statement.
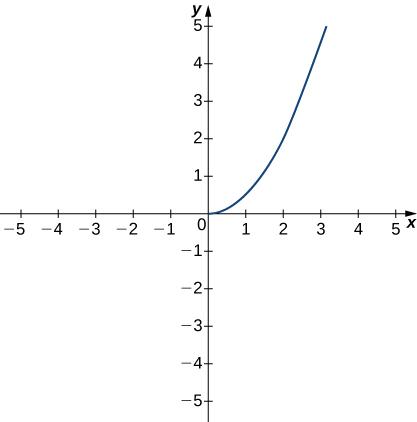
180) If \(0<|x−2|<δ\), then \(|f(x)−2|<1\).
181) If \(0<|x−2|<δ\), then \(|f(x)−2|<0.5\).
- Answer:
- \(δ≤0.25\)
The following graph of the function f satisfies \(\displaystyle \lim_{x→3}\,f(x)=−1\). In the following exercises, determine a value of \(δ>0\) that satisfies each statement.
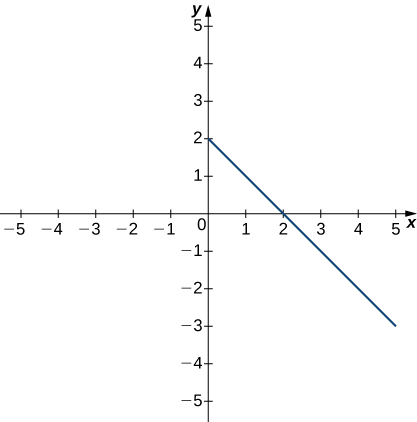
182) If \(0<|x−3|<δ\), then \(|f(x)+1|<1\).
183) If \(0<|x−3|<δ\), then \(|f(x)+1|<2\).
- Answer:
- \(δ≤2\)
In the following exercises, use the precise definition of limit to prove the given limits.
J3.7.1) \(\displaystyle \lim_{x→5}\,(2x - 1)=9\)
- Answer:
-
Let ε\(>0\); choose \(δ=\frac{ε}{2}\); assume \(0<|x−5|<δ\).
In other words:
\(0<|x - 5|<\frac{ε}{2}\),
so \(-\frac{ε}{2}<x - 5<\frac{ε}{2}\),
then \(-ε<2x - 10<ε\)
then |\(2x - 10|<ε\),
then |(\(2x - 1)−9\)|<ε
Thus, if \(0<|x−5|<δ\), then |(\(2x - 1)−9\)|<ε.
Therefore, by the definition of limit, \(\displaystyle \lim_{x→5}\,(2x - 1)=9\).
J3.7.2) \(\displaystyle \lim_{x→-3}\,(5x+2)=-13\)
J3.7.3) \(\displaystyle \lim_{x→-7^-}\,\frac{1}{x+7}= −∞ \)
- Answer:
-
Let \(M>0\); since this is a limit from the left, we need \(-δ<x+7<0\) to lead \(\frac{1}{x+7}<-M\) (since the limit is \(−∞ \))
Note: since \(x<-7, x+7<0\)Proof:
Let \(M>0\). Choose \(δ=\frac{1}{M}\).
If \(-δ<x+7<0\), in other words \(-\frac{1}{M}<x+7<0\)
then \(\frac{1}{M}>-(x+7)>0\) (both \(\frac{1}{M}\) and \(-(x+7)\) are positive)
then \(M<-\frac{1}{x+7}\)
then \(-M>\frac{1}{x+7}\)
so \(\frac{1}{x+7}<-M\)
Thus, if \(-\frac{1}{M}<x+7<0\) then\(\frac{1}{x+7}<-M\)
Therefore, by the definition of (infinite, from the left) limit, \(\displaystyle \lim_{x→-7^-}\,\frac{1}{x+7}= −∞ \).
J3.7.4) \(\displaystyle \lim_{x→2^+}\,\frac{1}{x-2}= ∞ \)
188) \(\displaystyle \lim_{x→2}\,(5x+8)=18\)
189) \(\displaystyle \lim_{x→3}\,\frac{x^2−9}{x−3}=6\)
- Answer:
- \(\frac{x^2−9}{x−3}\) is equivalent to \(x + 3\) by factoring, as long as \(x\) is not \(3\). Since we are looking at the limit as \(x→3\), we do not consider \(x=3\).
Let \(ε>0\), choose \(δ=ε\). If \(0<|x−3|<ε\), then \(|x+3−6|=|x−3|<ε\). Thus, by the definition of limit, \(\displaystyle \lim_{x→3}\,\frac{x^2−9}{x−3}=6\).
190) \(\displaystyle \lim_{x→2}\,\frac{2x^2−3x−2}{x−2}=5\)
191) \(\displaystyle \lim_{x→0}\,x^4=0\)
- Answer:
- Let \(ε>0\), choose\(δ=\sqrt[4]{ε}\) If \(0<|x|<\sqrt[4]{ε}\), then \(∣x^4∣=x^4<ε\). Thus, by the definition of limit, \(\displaystyle\lim_{x→0},x^4=0\).
192) \(\displaystyle \lim_{x→2}\,(x^2+2x)=8\)
Chapter Review Exercises
True or False. In the following exercises, justify your answer with a proof or a counterexample.
208) A function has to be continuous at \(x=a\) if the \(\displaystyle \lim_{x→a}\,f(x)\) exists.
209) Evaluate \(\displaystyle \lim_{x→0}\,\frac{sinx}{x}\) = ?
- Answer:
- 1
210) If there is a vertical asymptote at \(x=a\) for the function \(f(x)\), then f is undefined at the point \(x=a\).
211) If \(\displaystyle \lim_{x→a}\,f(x)\) does not exist, then f is undefined at the point \(x=a\).
- Answer:
- False. A removable discontinuity is possible.
212) Using the graph, find each limit or explain why the limit does not exist.
a. \(\displaystyle \lim_{x→−1}\,f(x)\)
b. \(\displaystyle \lim_{x→1}\,f(x)\)
c. \(\displaystyle \lim_{x→0^+}\,f(x)\)
d. \(\displaystyle \lim_{x→2}\,f(x)\)
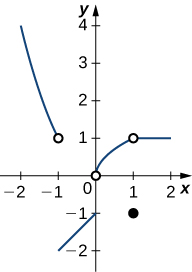
In the following exercises, evaluate the limit algebraically or explain why the limit does not exist.
213) \(\displaystyle \lim_{x→2}\,\frac{2x^2−3x−2}{x−2}\)
- Answer:
- 5
214) \(\displaystyle \lim_{x→0}\,3x^2−2x+4\)
215) \(\displaystyle \lim_{x→3}\,\frac{x^3−2x^2−1}{3x−2}\)
- Answer:
- 8/7
216) \(\displaystyle \lim_{x→π/2}\,\frac{cotx}{cosx}\)
217) \(\displaystyle \lim_{x→−5}\,\frac{x^2+25}{x+5}\)
- Answer:
- DNE
218) \(\displaystyle \lim_{x→2}\,\frac{3x^2−2x−8}{x^2−4}\)
219) \(\displaystyle \lim_{x→1}\,\frac{x^2−1}{x^3−1}\)
- Answer:
- 2/3
220) \(\displaystyle \lim_{x→1}\,\frac{x^2−1}{\sqrt{x}−1}\)
221) \(\displaystyle \lim_{x→4}\,\frac{4−x}{\sqrt{x}−2}\)
- Answer:
- −4
222) \(\displaystyle \lim_{x→4}\,\frac{1}{\sqrt{x}−2}\)
In the following exercises, use the squeeze theorem to prove the limit.
223) \(\displaystyle \lim_{x→0}\,x^2cos(2πx)=0\)
- Answer:
- Since \(−1≤cos(2πx)≤1\), then \(−x^2≤x^2cos(2πx)≤x^2\). Since \(lim_{x→0}\,x^2=0=lim_{x→0}\,−x^2\), it follows that \(lim_{x→0}\,x^2cos(2πx)=0\).
224) \(\displaystyle \lim_{x→0}\,x^3sin(\frac{π}{x})=0\)
225) Determine the domain such that the function \(f(x)=\sqrt{x−2}+xe^x\) is continuous over its domain.
- Answer:
- \([2,∞]\)
In the following exercises, determine the value of c such that the function remains continuous. Draw your resulting function to ensure it is continuous.
226) \(f(x)=\begin{cases}x^2+1 & x>c\\2^x & x≤c\end{cases}\)
227) \(f(x)=\begin{cases}\sqrt{x+1} & x>−1\\x^2+c & x≤−1\end{cases}\)
- Answer:
- \(c=-1\)
In the following exercises, use the precise definition of limit to prove the limit.
228) \(\displaystyle \lim_{x→1}\,(8x+16)=24\)
229) \(\displaystyle \lim_{x→0}\,x^3=0\)
- Answer:
- \(δ=\sqrt[3]{ε}\) [This is just a piece for constructing the proof.]
230) A ball is thrown into the air and the vertical position is given by \(x(t)=−4.9t^2+25t+5\). Use the Intermediate Value Theorem to show that the ball must land on the ground sometime between 5 sec and 6 sec after the throw.
231) A particle moving along a line has a displacement according to the function \(x(t)=t^2−2t+4\), where x is measured in meters and t is measured in seconds. Find the average velocity over the time period \(t=[0,2]\).
- Answer:
- \(0\) m/sec
232) From the previous exercises, estimate the instantaneous velocity at \(t=2\) by checking the average velocity within \(t=0.01\) sec.

