5.7E: Exercises for Integrals Resulting in Inverse Trigonometric Functions
- Page ID
- 17622
In exercises 1 - 6, evaluate each integral in terms of an inverse trigonometric function.
1) \(\displaystyle ∫^{\sqrt{3}/2}_0\frac{dx}{\sqrt{1−x^2}}\)
- Answer:
- \(\displaystyle ∫^{\sqrt{3}/2}_0\frac{dx}{\sqrt{1−x^2}} \quad = \quad \arcsin x\bigg|^{\sqrt{3}/2}_0=\dfrac{π}{3}\)
2) \(\displaystyle ∫^{1/2}_{−1/2}\frac{dx}{\sqrt{1−x^2}}\)
3) \(\displaystyle ∫^1_{\sqrt{3}}\frac{dx}{1+x^2}\)
- Answer:
- \(\displaystyle ∫^1_{\sqrt{3}}\frac{dx}{1+x^2} \quad = \quad \arctan x\bigg|^1_{\sqrt{3}}=−\dfrac{π}{12}\)
4) \(\displaystyle ∫^{\sqrt{3}}_{\frac{1}{\sqrt{3}}}\frac{dx}{1+x^2}\)
5) \(\displaystyle ∫^{\sqrt{2}}_1\frac{dx}{|x|\sqrt{x^2−1}}\)
- Answer:
- \(\displaystyle ∫^{\sqrt{2}}_1\frac{dx}{|x|\sqrt{x^2−1}} \quad = \quad \text{arcsec}\, x\bigg|^{\sqrt{2}}_1=\dfrac{π}{4}\)
6) \(\displaystyle ∫^{\frac{2}{\sqrt{3}}}_1\frac{dx}{|x|\sqrt{x^2−1}}\)
In exercises 7 - 12, find each indefinite integral, using appropriate substitutions.
7) \(\displaystyle ∫\frac{dx}{\sqrt{9−x^2}}\)
- Answer:
- \(\displaystyle ∫\frac{dx}{\sqrt{9−x^2}} \quad = \quad \arcsin \left(\frac{x}{3}\right)+C\)
8) \(\displaystyle ∫\frac{dx}{\sqrt{1−16x^2}}\)
- Answer:
- \(\displaystyle ∫\frac{dx}{\sqrt{1−16x^2}} = \frac{1}{4}∫\frac{4\,dx}{\sqrt{1−(4x)^2}} \quad = \quad \frac{1}{4}\arcsin \left(4x\right)+C\)
9) \(\displaystyle ∫\frac{dx}{9+x^2}\)
- Answer:
- \(\displaystyle ∫\frac{dx}{9+x^2} \quad = \quad \frac{1}{3}\arctan \left(\frac{x}{3}\right)+C\)
10) \(\displaystyle ∫\frac{dx}{25+16x^2}\)
- Answer:
- \(\displaystyle ∫\frac{dx}{25+16x^2} = ∫\frac{dx}{5^2+(4x)^2} = \frac{1}{4}∫\frac{4\,dx}{5^2+(4x)^2} = \frac{1}{4}\cdot\frac{1}{5}\arctan \left(\frac{4x}{5}\right)+C\quad = \quad \frac{1}{20}\arctan \left(\frac{4x}{5}\right)+C\)
11) \(\displaystyle ∫\frac{dx}{x\sqrt{x^2−9}}\)
- Answer:
- \(\displaystyle ∫\frac{dx}{x\sqrt{x^2−9}} \quad = \quad \frac{1}{3}\text{arcsec} \left(\frac{|x|}{3}\right)+C\)
12) \(\displaystyle ∫\frac{dx}{x\sqrt{4x^2−16}}\)
- Answer:
- \(\displaystyle ∫\frac{dx}{x\sqrt{4x^2−16}} = ∫\frac{2\,dx}{2x\sqrt{(2x)^2−4^2}} = ∫\frac{du}{u\sqrt{u^2−4^2}} = \frac{1}{4}\text{arcsec} \left(\frac{|u|}{4}\right)+C \quad = \quad \frac{1}{4}\text{arcsec} \left(\frac{|x|}{2}\right)+C\)
13) Explain the relationship \(\displaystyle −\arccos t+C=∫\frac{dt}{\sqrt{1−t^2}}=\arcsin t+C.\) Is it true, in general, that \(\arccos t=−\arcsin t\)?
- Answer:
- \(\cos(\frac{π}{2}−θ)=\sin θ.\) So, \(\arcsin t=\dfrac{π}{2}−\arccos t.\) They differ by a constant.
14) Explain the relationship \(\displaystyle \text{arcsec}\, t+C=∫\frac{dt}{|t|\sqrt{t^2−1}}=−\text{arccsc}\, t+C.\) Is it true, in general, that \(\text{arcsec}\, t=−\text{arccsc}\, t\)?
15) Explain what is wrong with the following integral: \(\displaystyle ∫^2_1\frac{dt}{\sqrt{1−t^2}}\).
- Answer:
- \(\sqrt{1−t^2}\) is not defined as a real number when \(t>1\).
16) Explain what is wrong with the following integral: \(\displaystyle ∫^1_{−1}\frac{dt}{|t|\sqrt{t^2−1}}\).
- Answer:
- \(\sqrt{t^2−1}\) is not defined as a real number when \(-1 \lt t \lt 1\), and the integrand is undefined when \(t = -1\) or \(t = 1\).
In exercises 17 - 20, solve for the antiderivative of \(f\) with \(C=0\), then use a calculator to graph \(f\) and the antiderivative over the given interval \([a,b]\). Identify a value of \(C\) such that adding \(C\) to the antiderivative recovers the definite integral \(\displaystyle F(x)=∫^x_af(t)\,dt\).
17) [T] \(\displaystyle ∫\frac{1}{\sqrt{9−x^2}}\,dx\) over \([−3,3]\)
- Answer:
-
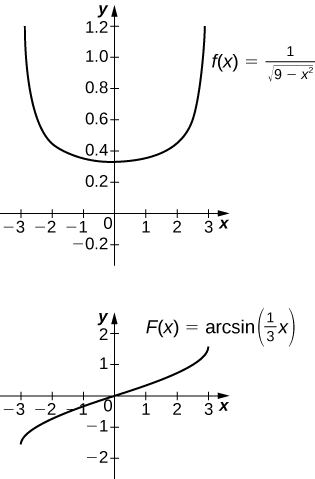
The antiderivative is \( \arcsin (\frac{x}{3})+C\). Taking \(C=\frac{π}{2}\) recovers the definite integral.
18) [T] \(\displaystyle ∫\frac{9}{9+x^2}\,dx\) over \([−6,6]\)
19) [T] \(\displaystyle ∫\frac{\cos x}{4+\sin^2x}\,dx\) over \([−6,6]\)
- Answer:
-
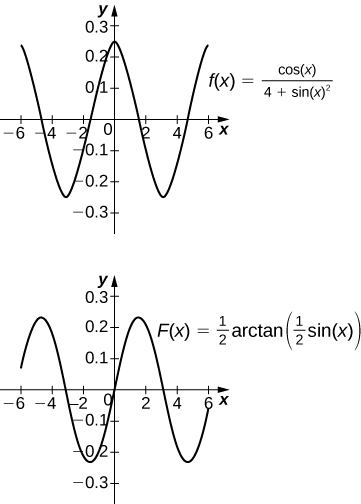
The antiderivative is \(\frac{1}{2}\arctan (\frac{\sin x}{2})+C\). Taking \(C=\frac{1}{2}\arctan (\frac{\sin(6)}{2})\) recovers the definite integral.
20) [T] \(\displaystyle ∫\frac{e^x}{1+e^{2x}}\,dx\) over \([−6,6]\)
In exercises 21 - 26, compute the antiderivative using appropriate substitutions.
21) \(\displaystyle ∫\frac{\arcsin t}{\sqrt{1−t^2}}\,dt\)
- Answer:
- \(\displaystyle ∫\frac{\arcsin t\,dt}{\sqrt{1−t^2}} \quad = \quad \tfrac{1}{2}(\arcsin t)^2+C\)
22) \(\displaystyle ∫\frac{dt}{\arcsin t\sqrt{1−t^2}}\)
- Answer:
- \(\displaystyle ∫\frac{dt}{\arcsin t\sqrt{1−t^2}} \quad = \quad \ln\left|\arcsin t\right|+C\)
23) \(\displaystyle ∫\frac{\arctan (2t)}{1+4t^2}\,dt\)
- Answer:
- \(\displaystyle ∫\frac{\arctan (2t)}{1+4t^2}\,dt \quad = \quad \frac{1}{4}(\arctan (2t))^2+C\)
24) \(\displaystyle ∫\frac{t\arctan (t^2)}{1+t^4}\,dt\)
- Answer:
- \(\displaystyle ∫\frac{t\arctan (t^2)}{1+t^4}\,dt = \frac{1}{2}∫u\,du = \frac{1}{2}\cdot\frac{u^2}{2}+C\quad = \quad \frac{\left(\arctan \left(t^2\right)\right)^2}{4}+C\)
25) \(\displaystyle ∫\frac{\text{arcsec} \left(\tfrac{t}{2}\right)}{|t|\sqrt{t^2−4}}\,dt\)
- Answer:
- \(\displaystyle ∫\frac{\text{arcsec} \left(\tfrac{t}{2}\right)}{|t|\sqrt{t^2−4}}\,dt \quad = \quad \tfrac{1}{4}(\text{arcsec} \left(\tfrac{t}{2}\right))^2+C\)
26) \(\displaystyle ∫\frac{t\,\text{arcsec} (t^2)}{t^2\sqrt{t^4−1}}\,dt\)
In exercises 27 - 32, use a calculator to graph the antiderivative of \(f\) with \(C=0\) over the given interval \([a,b].\) Approximate a value of \(C\), if possible, such that adding \(C\) to the antiderivative gives the same value as the definite integral \(\displaystyle F(x)=∫^x_af(t)\,dt.\)
27) [T] \(\displaystyle ∫\frac{1}{x\sqrt{x^2−4}}\,dx\) over \([2,6]\)
- Answer:
-
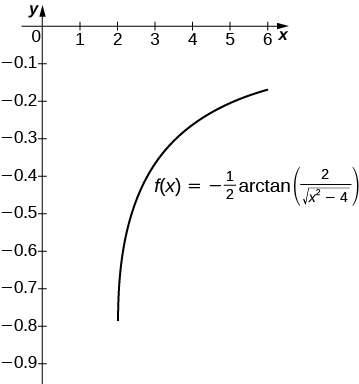
The antiderivative is \(\frac{1}{2}\text{arcsec} (\frac{x}{2})+C\). Taking \(C=0\) recovers the definite integral over \( [2,6]\).
28) [T] \(\displaystyle ∫\frac{1}{(2x+2)\sqrt{x}}\,dx\) over \([0,6]\)
29) [T] \(\displaystyle ∫\frac{(\sin x+x\cos x)}{1+x^2\sin^2x\,dx}\) over \( [−6,6]\)
- Answer:
-
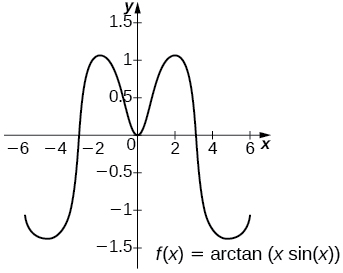
The general antiderivative is \(\arctan (x\sin x)+C\). Taking \(C=−\arctan (6\sin(6))\) recovers the definite integral.
30) [T] \(\displaystyle ∫\frac{2e^{−2x}}{\sqrt{1−e^{−4x}}}\,dx\) over \([0,2]\)
31) [T] \(\displaystyle ∫\frac{1}{x+x\ln 2x}\) over \([0,2]\)
- Answer:
-
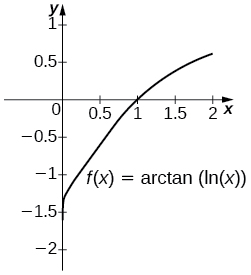
The general antiderivative is \(\arctan (\ln x)+C\). Taking \(\displaystyle C=\tfrac{π}{2}=\lim_{t \to ∞}\arctan t\) recovers the definite integral.
32) [T] \(\displaystyle ∫\frac{\arcsin x}{\sqrt{1−x^2}}\) over \([−1,1]\)
In exercises 33 - 38, compute each integral using appropriate substitutions.
33) \(\displaystyle ∫\frac{e^t}{\sqrt{1−e^{2t}}}\,dt\)
- Answer:
- \(\displaystyle ∫\frac{e^t}{\sqrt{1−e^{2t}}}\,dt \quad = \quad \arcsin (e^t)+C\)
34) \(\displaystyle ∫\frac{e^t}{1+e^{2t}}\,dt\)
- Answer:
- \(\displaystyle ∫\frac{e^t}{1+e^{2t}}\,dt = ∫\frac{e^t}{1+(e^t)^2}\,dt = ∫\frac{du}{1+u^2} \quad = \quad \arctan (e^t)+C\)
35) \(\displaystyle ∫\frac{dt}{t\sqrt{1−\ln^2t}}\)
- Answer:
- \(\displaystyle ∫\frac{dt}{t\sqrt{1−\ln^2t}} \quad = \quad \arcsin (\ln t)+C\)
36) \(\displaystyle ∫\frac{dt}{t(1+\ln^2t)}\)
- Answer:
- \(\displaystyle ∫\frac{dt}{t(1+\ln^2t)} \quad = \quad \arctan (\ln t)+C\)
37) \(\displaystyle ∫\frac{\arccos (2t)}{\sqrt{1−4t^2}}\,dt\)
- Answer:
- \(\displaystyle ∫\frac{\arccos (2t)}{\sqrt{1−4t^2}}\,dt \quad = \quad −\frac{1}{2}(\arccos (2t))^2+C\)
38) \(\displaystyle ∫\frac{e^t\arccos (e^t)}{\sqrt{1−e^{2t}}}\,dt\)
- Answer:
- \(\displaystyle ∫\frac{e^t\arccos (e^t)}{\sqrt{1−e^{2t}}}\,dt \quad = \quad \frac{\left(\arccos (e^t)\right)^2}{2}+C\)
In exercises 39 - 42, compute each definite integral.
39) \(\displaystyle ∫^{1/2}_0\frac{\tan(\arcsin t)}{\sqrt{1−t^2}}\,dt\)
- Answer:
- \(\displaystyle ∫^{1/2}_0\frac{\tan(\arcsin t)}{\sqrt{1−t^2}}\,dt \quad = \quad \frac{1}{2}\ln\left(\frac{4}{3}\right)\)
40) \(\displaystyle ∫^{1/2}_{1/4}\frac{\tan(\arccos t)}{\sqrt{1−t^2}}\,dt\)
41) \(\displaystyle ∫^{1/2}_0\frac{\sin(\arctan t)}{1+t^2}\,dt\)
- Answer:
- \(\displaystyle ∫^{1/2}_0\frac{\sin(\arctan t)}{1+t^2}\,dt \quad = \quad 1−\frac{2}{\sqrt{5}}\)
42) \(\displaystyle ∫^{1/2}_0\frac{\cos(\arctan t)}{1+t^2}\,dt\)
In exercises 43 - 50, compute each integral using appropriate substitutions and additional techniques.
43) \(\displaystyle ∫\frac{5}{x^2 + 10x + 34}\,dx\)
- Answer:
- \(\displaystyle ∫\frac{5}{x^2 + 10x + 34}\,dx = 5∫\frac{1}{(x^2 + 10x + 25) + 9}\,dx = 5∫\frac{1}{(x+5)^2 + 3^2}\,dx \quad = \quad \frac{5}{3}\arctan\left( \frac{x+5}{3}\right) +C\)
44) \(\displaystyle ∫\frac{7}{x^2 - 2x + 5}\,dx\)
45) \(\displaystyle ∫\frac{2}{\sqrt{-x^2 + 8x + 3}}\,dx\)
- Answer:
- \(\displaystyle ∫\frac{2}{\sqrt{-x^2 + 8x + 3}}\,dx = ∫\frac{2}{\sqrt{(\sqrt{19})^2-(x-4)^2}}\,dx \quad = \quad 2\arcsin \left( \frac{x-4}{\sqrt{19}} \right) + C\)
46) \(\displaystyle ∫\frac{dx}{\sqrt{-x^2 - 16x}}\)
47) \(\displaystyle ∫\frac{5x}{x^4 - 16x^2 + 100}\,dx\)
- Answer:
- \(\displaystyle ∫\frac{5x}{x^4 - 16x^2 + 100}\,dx = \frac{5}{2}∫\frac{2x}{(x^2-8)^2 + 36}\,dx \quad = \quad \frac{5}{12}\arctan\left( \frac{x^2-8}{6} \right) + C\)
48) \(\displaystyle ∫\frac{x}{\sqrt{1-x^4}}\,dx\)
49) \(\displaystyle ∫\frac{8}{x \sqrt{x^4-9}}\,dx\)
- Answer:
- \(\displaystyle ∫\frac{8}{x \sqrt{x^4-9}}\,dx = \frac{8}{2}∫\frac{2x}{x^2\sqrt{(x^2)^2 - 3^2}}\,dx \quad = \quad \frac{4}{3}\text{arcsec}\left( \frac{x^2}{3} \right) + C\)
50) \(\displaystyle ∫\frac{5}{x \sqrt{x^4-16x^2}}\,dx\)
- Answer:
- \(\displaystyle ∫\frac{5}{x \sqrt{x^4-16x^2}}\,dx = ∫\frac{5}{|x|\sqrt{x^2 - 16}}\,dx \quad = \quad \frac{5}{4}\text{arcsec}\left( \frac{|x|}{4} \right) + C\)
51) \(\displaystyle ∫\frac{7x^3+5x}{x^4 +9}\,dx\)
- Answer:
- \(\displaystyle ∫\frac{7x^3+5x}{x^4 +9}\,dx = \frac{7}{4}∫\frac{4x^3}{x^4 +9}\,dx+\frac{5}{2}∫\frac{2x}{(x^2)^2 +3^2}\,dx\quad = \quad \frac{7}{4}\ln|x^4 + 9| + \frac{5}{6}\arctan\left( \frac{x^2}{3} \right) + C\)
52) \(\displaystyle ∫\frac{2x+5}{x^2 +49}\,dx\)
53) \(\displaystyle ∫\frac{2x-1}{\sqrt{36-25x^2}}\,dx\)
- Answer:
- \(\displaystyle ∫\frac{2x-1}{\sqrt{36-25x^2}}\,dx = \frac{2}{-50}∫\frac{-50x}{\sqrt{36-25x^2}}\,dx-\frac{1}{5}∫\frac{5}{\sqrt{6^2-(5x)^2}}\,dx\quad = \quad -\frac{2}{25}\sqrt{36-25x^2} - \frac{1}{5}\arcsin\left( \frac{5x}{6} \right) + C\)
54) \(\displaystyle\int \frac{3x^3+4x^2+2x-22}{x^2+3x+5}\,dx\)
55) \(\displaystyle\int \frac{-x^3+14x^2-46x-7}{x^2-7x+1}\,dx\)
- Answer:
- Use long division first, since the degree of the numerator is not less than the degree of the denominator.
\(\displaystyle \int \frac{-x^3+14x^2-46x-7}{x^2-7x+1}\,dx = \int \left( -x + 7 + \frac{4x-14}{x^2-7x+1} \right) \,dx \quad = \quad -\frac{x^2}{2} + 7x +2\ln| x^2 - 7x + 1 | + C\)
56) \(\displaystyle\int \frac{x^3-x}{x^2+4x+9}\,dx\)
57) \(\displaystyle\int \frac{x^2+5x-2}{x^2-10x+32}\,dx\)
- Answer:
- Use long division first, since the degree of the numerator is not less than the degree of the denominator.
\(\displaystyle \int \frac{x^2+5x-2}{x^2-10x+32}\,dx = \int \left( 1 + \frac{15x-34}{x^2-10x+32} \right) \,dx =\int \,dx+\frac{15}{2}\int \frac{2x-10}{x^2-10x+32} \,dx +41\int\frac{1}{(x-5)^2 + (\sqrt{7})^2}\,dx \quad = \quad x + \frac{15}{2} \ln| x^2-10x+32 | + \frac{41}{\sqrt{7}}\arctan\left( \frac{x-5}{\sqrt{7}} \right) + C\)
58) \(\displaystyle\int \frac{x^3}{x^2+9}\,dx\)
- Answer:
- Use long division first, since the degree of the numerator is not less than the degree of the denominator. Fill in missing terms with zero-terms.
\(\displaystyle \int \frac{x^3}{x^2+9}\,dx \quad = \quad \frac{x^2}{2} -\frac{9}{2}\ln(x^2 +9) + C\)
59) \(\displaystyle\int \frac{\cos (x)}{\sin^2 (x)+1}\,dx\)
- Answer:
- \(\displaystyle \int \frac{\cos (x)}{\sin^2 (x)+1}\,dx \quad = \quad \arctan(\sin x) + C\)
60) \(\displaystyle\int \frac{\cos (x)}{1-\sin^2 (x)}\,dx\)
- Answer:
- \( \begin{align*} \displaystyle \int \frac{\cos (x)}{1-\sin^2 (x)}\,dx &= \int\frac{\cos x}{\cos^2 x}\,dx \\[5pt]
&= \int \sec x\,dx = ∫\sec x\cdot\frac{\sec x + \tan x}{\sec x + \tan x}\,dx \\[5pt]
&= ∫\frac{(\sec^2 x + \sec x\tan x)}{\tan x + \sec x}\,dx \\[5pt]
&= \ln|\tan x + \sec x | + C \end{align*} \)
61) \(\displaystyle\int \frac{3x-3}{\sqrt{x^2-2x-6}}\,dx\)
- Answer:
- \(\displaystyle \int \frac{3x-3}{\sqrt{x^2-2x-6}}\,dx \quad = \quad 3\sqrt{x^2-2x-6} + C\)
62) \(\displaystyle\int \frac{x-3}{\sqrt{x^2-6x+8}}\,dx\)
63) For \(A>0\), compute \(\displaystyle I(A)=∫^{A}_{−A}\frac{dt}{1+t^2}\) and evaluate \(\displaystyle \lim_{a→∞}I(A)\), the area under the graph of \(\dfrac{1}{1+t^2}\) on \([−∞,∞]\).
- Answer:
- \(2\arctan (A)→π\) as \(A→∞\)
64) For \(1<B<∞\), compute \(\displaystyle I(B)=∫^B_1\frac{dt}{t\sqrt{t^2−1}}\) and evaluate \(\displaystyle \lim_{B→∞}I(B)\), the area under the graph of \(\frac{1}{t\sqrt{t^2−1}}\) over \([1,∞)\).
65) Use the substitution \(u=\sqrt{2}\cot x\) and the identity \(1+\cot^2x=\csc^2x\) to evaluate \(\displaystyle ∫\frac{dx}{1+\cos^2x}\). (Hint: Multiply the top and bottom of the integrand by \(\csc^2x\).)
- Answer:
- Using the hint, one has \(\displaystyle ∫\frac{\csc^2x}{\csc^2x+\cot^2x}\,dx=∫\frac{\csc^2x}{1+2\cot^2x}\,dx.\) Set \(u=\sqrt{2}\cot x.\) Then, \(du=−\sqrt{2}\csc^2x\) and the integral is \(\displaystyle −\tfrac{1}{\sqrt{2}}∫\frac{du}{1+u^2}=−\tfrac{\sqrt{2}}{2}\arctan u+C=\tfrac{\sqrt{2}}{2}\arctan (\sqrt{2}\cot x)+C\). If one uses the identity \(\arctan s+\arctan (\frac{1}{s})=\frac{π}{2}\), then this can also be written \(\tfrac{\sqrt{2}}{2}\arctan (\frac{\tan x}{\sqrt{2}})+C.\)
66) [T] Approximate the points at which the graphs of \(f(x)=2x^2−1\) and \(g(x)=(1+4x^2)^{−3/2}\) intersect, and approximate the area between their graphs accurate to three decimal places.
67) [T] Approximate the points at which the graphs of \(f(x)=x^2−1\) and \(f(x)=x^2−1\) intersect, and approximate the area between their graphs accurate to three decimal places.
- Answer:
- \(x≈±1.13525.\) The left endpoint estimate with \(N=100\) is 2.796 and these decimals persist for \(N=500\).
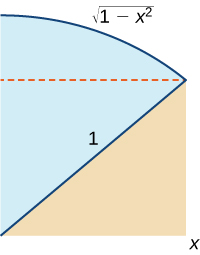
68) Use the following graph to prove that \(\displaystyle ∫^x_0\sqrt{1−t^2}\,dt=\frac{1}{2}x\sqrt{1−x^2}+\frac{1}{2}\arcsin x.\)
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.
- Paul Seeburger (Monroe Community College) edited this set to use alternate notation for all inverse trig functions and to add solutions for many even problems and to add new problems 43 - 53, except 48 and 50.
- Problems 48, 50, & 54 - 62 are from Apex Calculus.

