9.2E: Exercises for Infinite Series
- Last updated
- Save as PDF
- Page ID
- 18875
In exercises 1 - 4, use sigma notation to write each expressions as an infinite series.
1) \(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+⋯\)
- Answer
- \(\displaystyle \sum_{n=1}^∞\frac{1}{n}\)
2) \( 1−1+1−1+⋯\)
3) \( 1−\frac{1}{2}+\frac{1}{3}−\frac{1}{4}+...\)
- Answer
- \(\displaystyle \sum_{n=1}^∞\frac{(−1)^{n−1}}{n}\)
4) \( \sin 1+\sin \frac{1}{2}+\sin \frac{1}{3}+\sin \frac{1}{4}+⋯\)
In exercises 5 - 8, compute the first four partial sums \( S_1,…,S_4\) for the series having \( n^{\text{th}}\) term \( a_n\) starting with \( n=1\) as follows.
5) \( a_n=n\)
- Answer
- \( 1,3,6,10\)
6) \( a_n=1/n\)
7) \( a_n=\sin \frac{nπ}{2}\)
- Answer
- \( 1,1,0,0\)
8) \( a_n=(−1)^n\)
In exercises 9 - 12, compute the general term \( a_n\) of the series with the given partial sum \( S_n\). If the sequence of partial sums converges, find its limit \( S\).
9) \( S_n=1−\frac{1}{n}, \quad n≥2\)
- Answer
- \( a_n=S_n−S_{n−1}=\dfrac{1}{n−1}−\dfrac{1}{n}.\) Since \(\displaystyle S = \lim_{n\to\infty} S_n = \lim_{n\to\infty} \left(1−\frac{1}{n}\right) = 1,\) the series converges to \( S=1.\)
10) \( S_n=\dfrac{n(n+1)}{2}, \quad n≥1\)
11) \( S_n=\sqrt{n},\quad n≥2\)
- Answer
- \( a_n=S_n−S_{n−1}=\sqrt{n}−\sqrt{n−1}=\dfrac{1}{\sqrt{n−1}+\sqrt{n}}.\)
The series diverges because the partial sums are unbounded.
That is, \(\displaystyle \lim_{n\to\infty} S_n = \lim_{n\to\infty} \sqrt{n} = \infty.\)
12) \( S_n=2−\dfrac{n+2}{2^n},\quad n≥1\)
For each series in exercises 13 - 16, use the sequence of partial sums to determine whether the series converges or diverges.
13) \(\displaystyle \sum_{n=1}^∞\frac{n}{n+2}\)
- Answer
- \( S_1=1/3,\)
\( S_2=1/3+2/4>1/3+1/3=2/3,\)
\(S_3=1/3+2/4+3/5>3⋅(1/3)=1.\)
In general \( S_k>k/3,\) so the series diverges.
Note that the \(n^{\text{th}}\) Term Test for Divergence could also be used to prove that this series diverges.
14) \(\displaystyle \sum_{n=1}^∞(1−(−1)^n))\)
15) \(\displaystyle \sum_{n=1}^∞\frac{1}{(n+1)(n+2)}\) \(\quad\Big(\)Hint: Use a partial fraction decomposition like that for \(\displaystyle \sum_{n=1}^∞\frac{1}{n(n+1)}.\Big)\)
- Answer
-
\( S_1=1/(2\cdot 3)=1/6=2/3−1/2,\)
\( S_2=1/(2\cdot 3)+1/(3\cdot 4)=2/12+1/12=1/4=3/4−1/2,\)
\( S_3=1/(2\cdot 3)+1/(3\cdot 4)+1/(4\cdot 5)=10/60+5/60+3/60=3/10=4/5−1/2,\)
\( S_4=1/(2\cdot 3)+1/(3\cdot 4)+1/(4\cdot 5)+1/(5\cdot 6)=10/60+5/60+3/60+2/60=1/3=5/6−1/2.\)
The pattern is \( S_k=\dfrac{k+1}{k+2}−\dfrac{1}{2}.\)
Then \(\displaystyle \lim_{n\to\infty} S_n = \lim_{n\to\infty} \left( \dfrac{k+1}{k+2}−\dfrac{1}{2} \right) = \dfrac{1}{2},\) so the series converges to \( 1/2.\)
16) \(\displaystyle \sum_{n=1}^∞\frac{1}{2n+1}\) \(\quad\Big(\)Hint: Follow the reasoning for \(\displaystyle \sum_{n=1}^∞\frac{1}{n}.\Big)\)
Suppose that \(\displaystyle \sum_{n=1}^∞a_n=1\), that \(\displaystyle \sum_{n=1}^∞b_n=−1\), that \( a_1=2\), and \( b_1=−3\). Use this information to find the sum of the indicated series in exercises 17 - 20.
17) \(\displaystyle \sum_{n=1}^∞(a_n+b_n)\)
- Answer
- \( \displaystyle \sum_{n=1}^∞(a_n+b_n) \quad = \quad \sum_{n=1}^∞ a_n + \sum_{n=1}^∞ b_n \quad = \quad 1 + (-1) \quad = \quad 0\)
18) \(\displaystyle \sum_{n=1}^∞(a_n−2b_n)\)
19) \(\displaystyle \sum_{n=2}^∞(a_n−b_n)\)
- Answer
- \(\displaystyle \sum_{n=2}^∞(a_n−b_n) \quad = \quad \sum_{n=2}^∞ a_n - \sum_{n=2}^∞ b_n \quad = \quad \left(\sum_{n=1}^∞ a_n - a_1\right) - \left(\sum_{n=1}^∞ b_n -b_1\right) \quad = \quad (1 - 2) - (-1 - (-3)) = -1 - 2 \quad = \quad -3\)
20) \(\displaystyle \sum_{n=1}^∞(3a_{n+1}−4b_{n+1})\)
In exercises 21 - 26, state whether the given series converges or diverges and explain why.
21) \(\displaystyle \sum_{n=1}^∞\frac{1}{n+1000}\) (Hint: Rewrite using a change of index.)
- Answer
- The series diverges, \(\displaystyle \sum_{n=1001}^∞\frac{1}{n}\)
22) \(\displaystyle \sum_{n=1}^∞\frac{1}{n+10^{80}}\) (Hint: Rewrite using a change of index.)
23) \( 1+\frac{1}{10}+\frac{1}{100}+\frac{1}{1000}+⋯\)
- Answer
- This is a convergent geometric series, since \( r=\frac{1}{10}<1\)
24) \( 1+\frac{e}{π}+\frac{e^2}{π^2}+\frac{e^3}{π^3}+⋯\)
25) \( 1+\frac{π}{e^2}+\frac{π^2}{e^4}+\frac{π^3}{e^6}+\frac{π^4}{e^8}+⋯\)
- Answer
- This is a convergent geometric series, since \( r=π/e^2<1\)
26) \( 1−\sqrt{\frac{π}{3}}+\sqrt{\frac{π^2}{9}}−\sqrt{\frac{π^3}{27}}+⋯\)
For each \( a_n\) in exercises 27 - 30, write its sum as a geometric series of the form \(\displaystyle \sum_{n=1}^∞ar^n\). State whether the series converges and if it does, find the exact value of its sum.
27) \( a_1=−1\) and \( \dfrac{a_n}{a_{n+1}}=−5\) for \( n≥1.\)
- Answer
- \(\displaystyle \sum_{n=1}^∞5⋅(−1/5)^n\), converges to \( −5/6\)
28) \( a_1=2\) and \( \dfrac{a_n}{a_{n+1}}=1/2\) for \( n≥1.\)
29) \( a_1=10\) and \( \dfrac{a_n}{a_{n+1}}=10\) for \( n≥1\).
- Answer
- \(\displaystyle \sum_{n=1}^∞100⋅(1/10)^n,\) converges to \(\frac{100}{9}\)
30) \( a_1=\frac{1}{10}\) and \( a_n/a_{n+1}=−10\) for \( n≥1\).
In exercises 31 - 34, use the identity \(\displaystyle \frac{1}{1−y}=\sum_{n=0}^∞y^n\) (which is true for \(|y| < 1\)) to express each function as a geometric series in the indicated term.
31) \( \dfrac{x}{1+x}\) in \( x\)
- Answer
- \(\displaystyle x\sum_{n=0}^∞(−x)^n=\sum_{n=1}^∞(−1)^{n−1}x^n\)
32) \( \dfrac{\sqrt{x}}{1−x^{3/2}}\) in \( \sqrt{x}\)
33) \( \dfrac{1}{1+\sin^2x}\) in \(\sin x\)
- Answer
- \(\displaystyle \sum_{n=0}^∞(−1)^n\sin^{2n}(x)\)
34) \( \sec^2 x\) in \(\sin x\)
In exercises 35 - 38, evaluate the telescoping series or state whether the series diverges.
35) \(\displaystyle \sum_{n=1}^∞2^{1/n}−2^{1/(n+1)}\)
- Answer
- \( S_k=2−2^{1/(k+1)}→1\) as \( k→∞.\)
36) \(\displaystyle \sum_{n=1}^∞\frac{1}{n^{13}}−\frac{1}{(n+1)^{13}}\)
37) \(\displaystyle \sum_{n=1}^∞(\sqrt{n}−\sqrt{n+1})\)
- Answer
- \( S_k=1−\sqrt{k+1}\) diverges
38) \(\displaystyle \sum_{n=1}^∞(\sin n−\sin(n+1))\)
Express each series in exercises 39 - 42 as a telescoping sum and evaluate its \(n^{\text{th}}\) partial sum.
39) \(\displaystyle \sum_{n=1}^∞\ln\left(\frac{n}{n+1}\right)\)
- Answer
- \(\displaystyle \sum_{n=1}^∞[\ln n−\ln(n+1)],\)
\(S_k=−\ln(k+1)\)
40) \(\displaystyle \sum_{n=1}^∞\frac{2n+1}{(n^2+n)^2}\) (Hint: Factor denominator and use partial fractions.)
41) \(\displaystyle \sum_{n=2}^∞\frac{\ln\left(1+\frac{1}{n}\right)}{(\ln n)\ln(n+1)}\)
- Answer
- \( a_n=\frac{1}{\ln n}−\frac{1}{\ln(n+1)}\) and \( S_k=\frac{1}{\ln(2)}−\frac{1}{\ln(k+1)}→\frac{1}{\ln(2)}\)
42) \(\displaystyle \sum_{n=1}^∞\frac{(n+2)}{n(n+1)2^{n+1}}\) (Hint: Look at \( 1/(n2^n)\).
A general telescoping series is one in which all but the first few terms cancel out after summing a given number of successive terms.
43) Let \( a_n=f(n)−2f(n+1)+f(n+2),\) in which \( f(n)→0\) as \( n→∞.\) Find \(\displaystyle \sum_{n=1}^∞a_n\).
- Answer
- \(\displaystyle \sum_{n=1}^∞a_n=f(1)−f(2)\)
44) \( a_n=f(n)−f(n+1)−f(n+2)+f(n+3),\) in which \( f(n)→0\) as \( n→∞\). Find \(\displaystyle \sum_{n=1}^∞a_n\).
45) Suppose that \( a_n=c_0f(n)+c_1f(n+1)+c_2f(n+2)+c_3f(n+3)+c_4f(n+4),\) where \( f(n)→0\) as \( n→∞\). Find a condition on the coefficients \( c_0,…,c_4\) that make this a general telescoping series.
- Answer
- \( c_0+c_1+c_2+c_3+c_4=0\)
46) Evaluate \(\displaystyle \sum_{n=1}^∞\frac{1}{n(n+1)(n+2)}\) (Hint: \(\displaystyle \frac{1}{n(n+1)(n+2)}=\frac{1}{2n}−\frac{1}{n+1}+\frac{1}{2(n+2)}\))
47) Evaluate \(\displaystyle \sum_{n=2}^∞\frac{2}{n^3−n}.\)
- Answer
- \(\displaystyle \frac{2}{n^3−1}=\frac{1}{n−1}−\frac{2}{n}+\frac{1}{n+1},\)
\(S_n=(1−1+1/3)+(1/2−2/3+1/4) +(1/3−2/4+1/5)+(1/4−2/5+1/6)+⋯=1/2\)
48) Find a formula for \(\displaystyle \sum_{n=1}^∞\frac{1}{n(n+N)}\) where \( N\) is a positive integer.
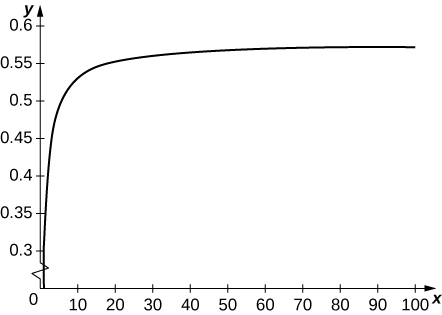
49) [T] Define a sequence \(\displaystyle t_k=\sum_{n=1}^{k−1}(1/k)−\ln k\). Use the graph of \( 1/x\) to verify that \( t_k\) is increasing. Plot \( t_k\) for \( k=1…100\) and state whether it appears that the sequence converges.
- Answer
-
\( t_k\) converges to \( 0.57721…t_k\) is a sum of rectangles of height \( 1/k\) over the interval \( [k,k+1]\) which lie above the graph of \( 1/x\).
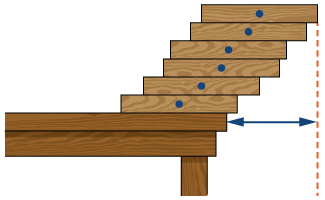
50) [T] Suppose that \( N\) equal uniform rectangular blocks are stacked one on top of the other, allowing for some overhang. Archimedes’ law of the lever implies that the stack of \( N\) blocks is stable as long as the center of mass of the top \( (N−1)\) blocks lies at the edge of the bottom block. Let \( x\) denote the position of the edge of the bottom block, and think of its position as relative to the center of the next-to-bottom block. This implies that \( (N−1)x=\left(\frac{1}{2}−x\right)\) or \( x=1/(2N)\). Use this expression to compute the maximum overhang (the position of the edge of the top block over the edge of the bottom block.) See the following figure.
Each of the following infinite series converges to the given multiple of \( π\) or \( 1/π\).
In each case, find the minimum value of \( N\) such that the \( N^{\text{th}}\) partial sum of the series accurately approximates the left-hand side to the given number of decimal places, and give the desired approximate value. Up to 15 decimals place, \( π=3.141592653589793....\)
51) [T] \(\displaystyle π=−3+\sum_{n=1}^∞\frac{n2^nn!^2}{(2n)!},\) error \( <0.0001\)
- Answer
- \(N=22,\)
\(S_N=6.1415\)
52) [T] \(\displaystyle \frac{π}{2}=\sum_{k=0}^∞\frac{k!}{(2k+1)!!}=\sum_{k=0}^∞\frac{2^kk!^2}{(2k+1)!},\) error \( <10^{−4}\)
53) [T] \(\displaystyle \frac{9801}{2π}=\frac{4}{9801}\sum_{k=0}^∞\frac{(4k)!(1103+26390k)}{(k!)^4396^{4k}},\) error \( <10^{−12}\)
- Answer
- \( N=3,\)
\(S_N=1.559877597243667...\)
54) [T] \(\displaystyle \frac{1}{12π}=\sum_{k=0}^∞\frac{(−1)^k(6k)!(13591409+545140134k)}{(3k)!(k!)^3640320^{3k+3/2}}\), error \( <10^{−15}\)
55) [T] A fair coin is one that has probability \( 1/2\) of coming up heads when flipped.
a. What is the probability that a fair coin will come up tails \( n\) times in a row?
b. Find the probability that a coin comes up heads for the first time after an even number of coin flips.
- Answer
- a. The probability of any given ordered sequence of outcomes for \( n\) coin flips is \( 1/2^n\).
b. The probability of coming up heads for the first time on the \( n\) th flip is the probability of the sequence \( TT…TH\) which is \( 1/2^n\). The probability of coming up heads for the first time on an even flip is \(\displaystyle \sum_{n=1}^∞1/2^{2n}\) or \( 1/3\).
56) [T] Find the probability that a fair coin is flipped a multiple of three times before coming up heads.
57) [T] Find the probability that a fair coin will come up heads for the second time after an even number of flips.
- Answer
- \(5/9\)
58) [T] Find a series that expresses the probability that a fair coin will come up heads for the second time on a multiple of three flips.
59) [T] The expected number of times that a fair coin will come up heads is defined as the sum over \( n=1,2,…\) of \( n\) times the probability that the coin will come up heads exactly \( n\) times in a row, or \( \dfrac{n}{2^{n+1}}\). Compute the expected number of consecutive times that a fair coin will come up heads.
- Answer
- \(\displaystyle E=\sum_{n=1}^∞\frac{n}{2^{n+1}}=1,\) as can be shown using summation by parts
60) [T] A person deposits \( $10\) at the beginning of each quarter into a bank account that earns \( 4%\) annual interest compounded quarterly (four times a year).
a. Show that the interest accumulated after \( n\) quarters is \( $10(\frac{1.01^{n+1}−1}{0.01}−n).\)
b. Find the first eight terms of the sequence.
c. How much interest has accumulated after \( 2\) years?
61) [T] Suppose that the amount of a drug in a patient’s system diminishes by a multiplicative factor \( r<1\) each hour. Suppose that a new dose is administered every \( N\) hours. Find an expression that gives the amount \( A(n)\) in the patient’s system after \( n\) hours for each \( n\) in terms of the dosage \( d\) and the ratio \( r\). (Hint: Write \( n=mN+k\), where \( 0≤k<N\), and sum over values from the different doses administered.)
- Answer
- The part of the first dose after \( n\) hours is \( dr^n\), the part of the second dose is \( dr^{n−N}\), and, in general, the part remaining of the \( m^{\text{th}}\) dose is \( dr^{n−mN}\), so \(\displaystyle A(n)=\sum_{l=0}^mdr^{n−lN}=\sum_{l=0}^mdr^{k+(m−l)N}=\sum_{q=0}^mdr^{k+qN}=dr^k\sum_{q=0}^mr^{Nq}=dr^k\frac{1−r^{(m+1)N}}{1−r^N},\;\text{where}\,n=k+mN.\)
62) [T] A certain drug is effective for an average patient only if there is at least \( 1\) mg per kg in the patient’s system, while it is safe only if there is at most \( 2\) mg per kg in an average patient’s system. Suppose that the amount in a patient’s system diminishes by a multiplicative factor of \( 0.9\) each hour after a dose is administered. Find the maximum interval \( N\) of hours between doses, and corresponding dose range \( d\) (in mg/kg) for this \( N\) that will enable use of the drug to be both safe and effective in the long term.
63) Suppose that \( a_n≥0\) is a sequence of numbers. Explain why the sequence of partial sums of \( a_n\) is increasing.
- Answer
- \( S_{N+1}=a_{N+1}+S_N≥S_N\)
64) [T] Suppose that \( a_n\) is a sequence of positive numbers and the sequence \( S_n\) of partial sums of \( a_n\) is bounded above. Explain why \(\displaystyle \sum_{n=1}^∞a_n\) converges. Does the conclusion remain true if we remove the hypothesis \( a_n≥0\)?
65) [T] Suppose that \( a_1=S_1=1\) and that, for given numbers \( S>1\) and \( 0<k<1\), one defines \( a_{n+1}=k(S−S_n)\) and \( S_{n+1}=a_{n+1}+S_n\). Does \( S_n\) converge? If so, to what? (Hint: First argue that \( S_n<S\) for all \( n\) and \( S_n\) is increasing.)
- Answer
- Since \( S>1, a_2>0,\) and since \( k<1, S_2=1+a_2<1+(S−1)=S\). If \( S_n>S\) for some \( n\), then there is a smallest \( n\). For this \( n, S>S_{n−1}\), so \( S_n=S_{n−1}+k(S−S_{n−1})=kS+(1−k)S_{n−1}<S\), a contradiction. Thus \( S_n<S\) and \( a_{n+1}>0\) for all \( n\), so \( S_n\) is increasing and bounded by \( S\). Let \(\displaystyle S_∗=\lim S_n\). If \( S_∗<S\), then \( δ=k(S−S_∗)>0\), but we can find n such that \( S_∗−S_n<δ/2\), which implies that \( S_{n+1}=S_n+k(S−S_n) >S_∗+δ/2\), contradicting that Sn is increasing to \( S_∗\). Thus \( S_n→S.\)
66) [T] A version of von Bertalanffy growth can be used to estimate the age of an individual in a homogeneous species from its length if the annual increase in year \( n+1\) satisfies \( a_{n+1}=k(S−S_n)\), with \( S_n\) as the length at year \( n, S\) as a limiting length, and \( k\) as a relative growth constant. If \( S_1=3, S=9,\) and \( k=1/2,\) numerically estimate the smallest value of n such that \( S_n≥8\). Note that \( S_{n+1}=S_n+a_{n+1}.\) Find the corresponding \( n\) when \( k=1/4.\)
67) [T] Suppose that \(\displaystyle \sum_{n=1}^∞a_n\) is a convergent series of positive terms. Explain why \(\displaystyle \lim_{N→∞}\sum_{n=N+1}^∞a_n=0.\)
- Answer
- Let \(\displaystyle S_k=\sum_{n=1}^ka_n\) and \( S_k→L\). Then \( S_k\) eventually becomes arbitrarily close to \( L\), which means that \(\displaystyle L−S_N=\sum_{n=N+1}^∞a_n\) becomes arbitrarily small as \( N→∞.\)
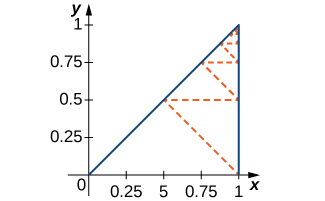
68) [T] Find the length of the dashed zig-zag path in the following figure.
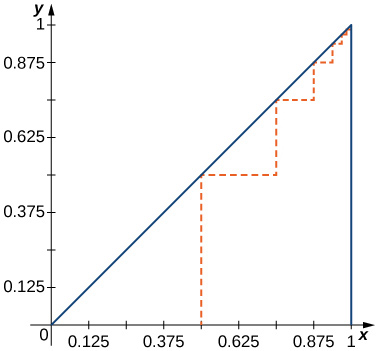
69) [T] Find the total length of the dashed path in the following figure.
- Answer
- \(\displaystyle L=\left(1+\frac{1}{2}\right)\sum_{n=1}^∞\frac{1}{2^n}=\frac{3}{2}\).
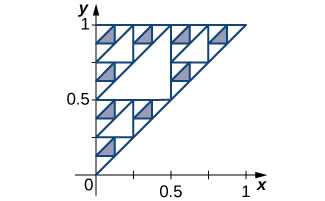
70) [T] The Sierpinski triangle is obtained from a triangle by deleting the middle fourth as indicated in the first step, by deleting the middle fourths of the remaining three congruent triangles in the second step, and in general deleting the middle fourths of the remaining triangles in each successive step. Assuming that the original triangle is shown in the figure, find the areas of the remaining parts of the original triangle after \( N\) steps and find the total length of all of the boundary triangles after \( N\) steps.
71) [T] The Sierpinski gasket is obtained by dividing the unit square into nine equal sub-squares, removing the middle square, then doing the same at each stage to the remaining sub-squares. The figure shows the remaining set after four iterations. Compute the total area removed after \( N\) stages, and compute the length the total perimeter of the remaining set after \( N\) stages.

- Answer
- At stage one a square of area \( 1/9\) is removed, at stage \( 2\) one removes \( 8\) squares of area \( 1/9^2\), at stage three one removes \( 8^2\) squares of area \( 1/9^3\), and so on. The total removed area after \( N\) stages is \(\displaystyle \sum_{n=0}^{N−1}\frac{8^N}{9^{N+1}}=\frac{1}{8}\cdot\frac{1−(8/9)^N}{1−8/9}→1\) as \(N→∞.\) The total perimeter is \(\displaystyle 4+4\sum_{n=0}^∞\frac{8^N}{3^{N+1}}→∞.\)


