12.5E: Exercises for Section 12.5
- Page ID
- 10582
Finding Components of Acceleration & Kepler's Laws
1) Find the tangential and normal components of acceleration for \(\vecs r(t)=t^2\,\hat{\mathbf{i}}+2t \,\hat{\mathbf{j}}\) when \(t=1\).
- Answer:
- \(a_\vecs{T}=\sqrt{2}, \quad a_\vecs{N}=\sqrt{2}\)
In questions 2 - 8, find the tangential and normal components of acceleration.
2) \(\vecs r(t)=⟨\cos(2t),\,\sin(2t),1⟩\)
3) \(\vecs r(t)=⟨e^t \cos t,\,e^t\sin t,\,e^t⟩\). The graph is shown here:
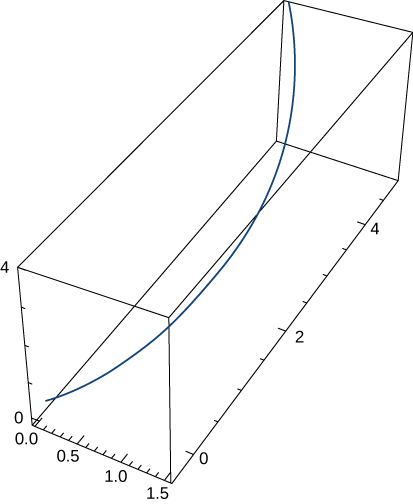
- Answer:
- \(a_\vecs{T}=\sqrt{3}e^t, \quad a_\vecs{N}=\sqrt{2}e^t\)
4) \(\vecs r(t)=⟨\frac{2}{3}(1+t)^{3/2}, \,\frac{2}{3}(1-t)^{3/2},\,\sqrt{2}t⟩\)
5) \(\vecs r(t)=\left\langle 2t,\,t^2,\,\dfrac{t^3}{3}\right\rangle\)
- Answer:
- \(a_\vecs{T}=2t, \quad a_\vecs{N}=2\)
6) \(\vecs r(t)=t^2\,\hat{\mathbf{i}}+t^2\,\hat{\mathbf{j}}+t^3\,\hat{\mathbf{k}}\)
7) \(\vecs r(t)=⟨6t,\,3t^2,\,2t^3⟩\)
- Answer:
- \(a_\vecs{T}=\dfrac{6t +12t^3}{\sqrt{1+t^2+t^4}}, \quad a_\vecs{N}=6\sqrt{\dfrac{1+4t^2+t^4}{1+t^2+t^4}}\)
8) \(\vecs r(t)=3\cos(2πt)\,\hat{\mathbf{i}}+3\sin(2πt)\,\hat{\mathbf{j}}\)
- Answer:
- \(a_\vecs{T}=0, \quad a_\vecs{N}=12\pi^2\)
9) Find the tangential and normal components of acceleration for \(\vecs r(t)=a\cos(ωt)\,\hat{\mathbf{i}}+b\sin(ωt)\,\hat{\mathbf{j}}\) at \(t=0\).
- Answer:
- \(a_\vecs{T}=0, \quad a_\vecs{N}=aω^2\)
10) Suppose that the position function for an object in three dimensions is given by the equation \(\vecs r(t)=t\cos(t)\,\hat{\mathbf{i}}+t\sin(t)\,\hat{\mathbf{j}}+3t\,\hat{\mathbf{k}}\).
a. Show that the particle moves on a circular cone.
b. Find the angle between the velocity and acceleration vectors when \(t=1.5\).
c. Find the tangential and normal components of acceleration when \(t=1.5\).
- Answer:
- c. \(a_\vecs{T}=0.43\,\text{m/sec}^2, \quad a_\vecs{N}=2.46\,\text{m/sec}^2\)
11) The force on a particle is given by \(\vecs f(t)=(\cos t)\,\hat{\mathbf{i}}+(\sin t)\,\hat{\mathbf{j}}\). The particle is located at point \((c,0)\) at \(t=0\). The initial velocity of the particle is given by \(\vecs v(0)=v_0\,\hat{\mathbf{j}}\). Find the path of the particle of mass \(m\). (Recall, \(\vecs F=m\vecs a\).)
- Answer:
- \(\vecs r(t)=\left(\dfrac{-\cos t}{m}+c+\frac{1}{m}\right)\,\hat{\mathbf{i}}+\left(\dfrac{−\sin t}{m}+\left(v_0+\frac{1}{m}\right)t\right)\,\hat{\mathbf{j}}\)
12) An automobile that weighs \(2700\) lb makes a turn on a flat road while traveling at \(56\) ft/sec. If the radius of the turn is \(70\) ft, what is the required frictional force to keep the car from skidding?
13) Using Kepler’s laws, it can be shown that \(v_0=\sqrt{\dfrac{2GM}{r_0}}\) is the minimum speed needed when \(\theta=0\) so that an object will escape from the pull of a central force resulting from mass \(M\). Use this result to find the minimum speed when \(\theta=0\) for a space capsule to escape from the gravitational pull of Earth if the probe is at an altitude of \(300\) km above Earth’s surface.
- Answer:
- \(10.94\) km/sec
14) Find the time in years it takes the dwarf planet Pluto to make one orbit about the Sun given that \(a=39.5\) A.U.
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.


