15E: Vector Calculus (Exercises)
- Page ID
- 10941
1. The domain of vector field \(\vecs{F}=\vecs{F}(x,y)\) is a set of points \((x,y)\) in a plane, and the range of \(\vecs F\) is a set of what in the plane?
- Answer:
- Vectors
For exercises 2 - 4, determine whether the statement is true or false.
2. Vector field \(\vecs{F}(x,y)=⟨3x^2,1⟩\) is a gradient field for both \(ϕ_1(x,y)=x^3+y\) and \(ϕ_2(x,y)=y+x^3+100.\)
3. Vector field \(\vecs{F}(x,y)=\dfrac{⟨y,x⟩}{\sqrt{x^2+y^2}}\) is constant in direction and magnitude on a unit circle.
- Answer:
- False
4. Vector field \(\vecs{F}=\dfrac{⟨y,x⟩}{\sqrt{x^2+y^2}}\) is neither a radial field nor a rotation field.
For exercises 5 - 13, describe each vector field by drawing some of its vectors.
5. [T] \(\vecs{F}(x,y)=x\,\hat{\mathbf i}+y\,\hat{\mathbf j}\)
- Answer:
-
6. [T] \(\vecs{F}(x,y)=−y\,\hat{\mathbf i}+x\,\hat{\mathbf j}\)
7. [T] \(\vecs{F}(x,y)=x\,\hat{\mathbf i}−y\,\hat{\mathbf j}\)
- Answer:
-
8. [T] \(\vecs{F}(x,y)=\,\hat{\mathbf i}+\,\hat{\mathbf j}\)
9. [T] \(\vecs{F}(x,y)=2x\,\hat{\mathbf i}+3y\,\hat{\mathbf j}\)
- Answer:
-
10. [T] \(\vecs{F}(x,y)=3\,\hat{\mathbf i}+x\,\hat{\mathbf j}\)
11. [T] \(\vecs{F}(x,y)=y\,\hat{\mathbf i}+\sin x\,\hat{\mathbf j}\)
- Answer:
-
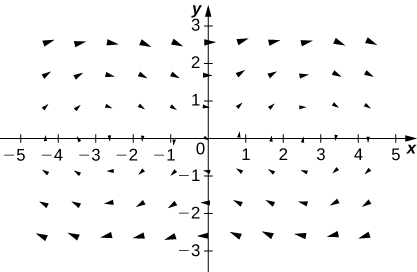
12. [T] \(\vecs F(x,y,z)=x\,\hat{\mathbf i}+y\,\hat{\mathbf j}+z\,\hat{\mathbf k}\)
13. [T] \(\vecs F(x,y,z)=2x\,\hat{\mathbf i}−2y\,\hat{\mathbf j}−2z\,\hat{\mathbf k}\)
- Answer:
-
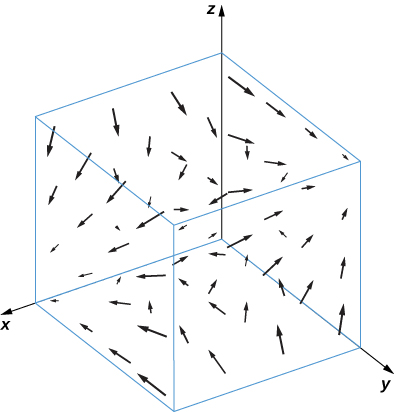
14. [T] \(\vecs F(x,y,z)=yz\,\hat{\mathbf i}−xz\,\hat{\mathbf j}\)
For exercises 15 - 20, find the gradient vector field of each function \(f\).
15. \(f(x,y)=x\sin y+\cos y\)
- Answer:
- \(\vecs{F}(x,y)=\sin(y)\,\hat{\mathbf i}+(x\cos y−\sin y)\,\hat{\mathbf j}\)
16. \(f(x,y,z)=ze^{−xy}\)
17. \(f(x,y,z)=x^2y+xy+y^2z\)
- Answer:
- \(\vecs F(x,y,z)=(2xy+y)\,\hat{\mathbf i}+(x^2+x+2yz)\,\hat{\mathbf j}+y^2\,\hat{\mathbf k}\)
18. \(f(x,y)=x^2\sin(5y)\)
19. \(f(x,y)=\ln(1+x^2+2y^2)\)
- Answer:
- \(\vecs{F}(x,y)=\dfrac{2x}{1+x^2+2y^2}\,\hat{\mathbf i}+\dfrac{4y}{1+x^2+2y^2}\,\hat{\mathbf j}\)
20. \(f(x,y,z)=x\cos\left(\frac{y}{z}\right)\)
21. What is vector field \(\vecs{F}(x,y)\) with a value at \((x,y)\) that is of unit length and points toward \((1,0)\)?
- Answer:
- \(\vecs{F}(x,y)=\dfrac{(1−x)\,\hat{\mathbf i}−y\,\hat{\mathbf j}}{\sqrt{(1−x)^2+y^2}}\)
For exercises 22 - 24, write formulas for the vector fields with the given properties.
22. All vectors are parallel to the \(x\)-axis and all vectors on a vertical line have the same magnitude.
23. All vectors point toward the origin and have constant length.
- Answer:
- \(\vecs{F}(x,y)=\dfrac{(y\,\hat{\mathbf i}−x\,\hat{\mathbf j})}{\sqrt{x^2+y^2}}\)
24. All vectors are of unit length and are perpendicular to the position vector at that point.
25. Give a formula \(\vecs{F}(x,y)=M(x,y)\,\hat{\mathbf i}+N(x,y)\,\hat{\mathbf j}\) for the vector field in a plane that has the properties that \(\vecs{F}=\vecs 0\) at \((0,0)\) and that at any other point \((a,b), \vecs F\) is tangent to circle \(x^2+y^2=a^2+b^2\) and points in the clockwise direction with magnitude \(\|\vecs F\|=\sqrt{a^2+b^2}\).
- Answer:
- \(\vecs{F}(x,y)=y\,\hat{\mathbf i}−x\,\hat{\mathbf j}\)
26. Is vector field \(\vecs{F}(x,y)=(P(x,y),Q(x,y))=(\sin x+y)\,\hat{\mathbf i}+(\cos y+x)\,\hat{\mathbf j}\) a gradient field?
27. Find a formula for vector field \(\vecs{F}(x,y)=M(x,y)\,\hat{\mathbf i}+N(x,y)\,\hat{\mathbf j}\) given the fact that for all points \((x,y)\), \(\vecs F\) points toward the origin and \(\|\vecs F\|=\dfrac{10}{x^2+y^2}\).
- Answer:
- \(\vecs{F}(x,y)=\dfrac{−10}{(x^2+y^2)^{3/2}}(x\,\hat{\mathbf i}+y\,\hat{\mathbf j})\)
For exercises 28 - 29, assume that an electric field in the \(xy\)-plane caused by an infinite line of charge along the \(x\)-axis is a gradient field with potential function \(V(x,y)=c\ln\left(\frac{r_0}{\sqrt{x^2+y^2}}\right)\), where \(c>0\) is a constant and \(r_0\) is a reference distance at which the potential is assumed to be zero.
28. Find the components of the electric field in the \(x\)- and \(y\)-directions, where \(\vecs E(x,y)=−\vecs ∇V(x,y).\)
29. Show that the electric field at a point in the \(xy\)-plane is directed outward from the origin and has magnitude \(\|\vecs E\|=\dfrac{c}{r}\), where \(r=\sqrt{x^2+y^2}\).
- Answer:
- \(\|\vecs E\|=\dfrac{c}{|r|^2}r=\dfrac{c}{|r|}\dfrac{r}{|r|}\)
A flow line (or streamline) of a vector field \(\vecs F\) is a curve \(\vecs r(t)\) such that \(d\vecs{r}/dt=\vecs F(\vecs r(t))\). If \(\vecs F\) represents the velocity field of a moving particle, then the flow lines are paths taken by the particle. Therefore, flow lines are tangent to the vector field.
For exercises 30 and 31, show that the given curve \(\vecs c(t)\) is a flow line of the given velocity vector field \(\vecs F(x,y,z)\).
30. \(\vecs c(t)=⟨ e^{2t},\ln|t|,\frac{1}{t} ⟩,\,t≠0;\quad \vecs F(x,y,z)=⟨2x,z,−z^2⟩\)
31. \(\vecs c(t)=⟨ \sin t,\cos t,e^t⟩;\quad \vecs F(x,y,z) =〈y,−x,z〉\)
- Answer:
- \(\vecs c′(t)=⟨ \cos t,−\sin t,e^{−t}⟩=\vecs F(\vecs c(t))\)
For exercises 32 - 34, let \(\vecs{F}=x\,\hat{\mathbf i}+y\,\hat{\mathbf j}\), \(\vecs G=−y\,\hat{\mathbf i}+x\,\hat{\mathbf j}\), and \(\vecs H=x\,\hat{\mathbf i}−y\,\hat{\mathbf j}\). Match \(\vecs F\), \(\vecs G\), and \(\vecs H\) with their graphs.
32.
33.
- Answer:
- \(\vecs H\)
34.
For exercises 35 - 38, let \(\vecs{F}=x\,\hat{\mathbf i}+y\,\hat{\mathbf j}\), \(\vecs G=−y\,\hat{\mathbf i}+x\,\hat{\mathbf j}\), and \(\vecs H=−x\,\hat{\mathbf i}+y\,\hat{\mathbf j}\). Match the vector fields with their graphs in (I)−(IV).
- \(\vecs F+\vecs G\)
- \(\vecs F+\vecs H\)
- \(\vecs G+\vecs H\)
- \(−\vecs F+\vecs G\)
35.
- Answer:
- d. \(−\vecs F+\vecs G\)
36.
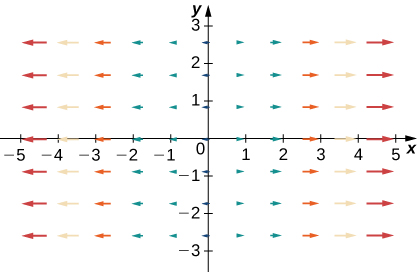
37.
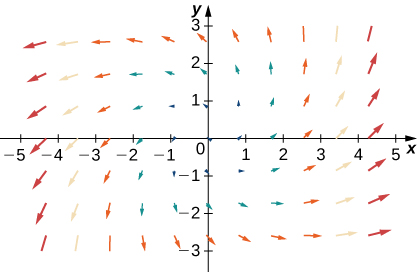
- Answer:
- a. \(\vecs F+\vecs G\)
38.
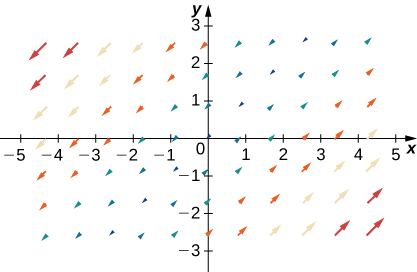
16.2: Line Integrals
1. True or False? Line integral \(\displaystyle\int _C f(x,y)\,ds\) is equal to a definite integral if \(C\) is a smooth curve defined on \([a,b]\) and if function \(f\) is continuous on some region that contains curve \(C\).
- Answer:
- True
2. True or False? Vector functions \(\vecs r_1=t\,\hat{\mathbf i}+t^2\,\hat{\mathbf j}, \quad 0≤t≤1,\) and \(\vecs r_2=(1−t)\,\hat{\mathbf i}+(1−t)^2\,\hat{\mathbf j}, \quad 0≤t≤1\), define the same oriented curve.
3. True or False? \(\displaystyle\int _{−C}(P\,dx+Q\,dy)=\int _C(P\,dx−Q\,dy)\)
- Answer:
- False
4. True or False? A piecewise smooth curve \(C\) consists of a finite number of smooth curves that are joined together end to end.
5. True or False? If \(C\) is given by \(x(t)=t,\quad y(t)=t, \quad 0≤t≤1\), then \(\displaystyle\int _Cxy\,ds=\int ^1_0t^2\,dt.\)
- Answer:
- False
For the following exercises, use a computer algebra system (CAS) to evaluate the line integrals over the indicated path.
6. [T] \(\displaystyle\int _C(x+y)\,ds\)
\(C:x=t,y=(1−t),z=0\) from \((0, 1, 0)\) to \((1, 0, 0)\)
7. [T] \(\displaystyle \int _C(x−y)ds\)
\(C:\vecs r(t)=4t\,\hat{\mathbf i}+3t\,\hat{\mathbf j}\) when \(0≤t≤2\)
- Answer:
- \(\displaystyle\int _C(x−y)\,ds=10\)
8. [T] \(\displaystyle\int _C(x^2+y^2+z^2)\,ds\)
\(C:\vecs r(t)=\sin t\,\hat{\mathbf i}+\cos t\,\hat{\mathbf j}+8t\,\hat{\mathbf k}\) when \(0≤t≤\dfrac{π}{2}\)
9. [T] Evaluate \(\displaystyle\int _Cxy^4\,ds\), where \(C\) is the right half of circle \(x^2+y^2=16\) and is traversed in the clockwise direction.
- Answer:
- \(\displaystyle\int _Cxy^4\,ds=\frac{8192}{5}\)
10. [T] Evaluate \(\displaystyle\int _C4x^3ds\), where C is the line segment from \((−2,−1)\) to \((1, 2)\).
For the following exercises, find the work done.
11. Find the work done by vector field \(\vecs F(x,y,z)=x\,\hat{\mathbf i}+3xy\,\hat{\mathbf j}−(x+z)\,\hat{\mathbf k}\) on a particle moving along a line segment that goes from \((1,4,2)\) to \((0,5,1)\).
- Answer:
- \(W=8\) units of work
12. Find the work done by a person weighing 150 lb walking exactly one revolution up a circular, spiral staircase of radius 3 ft if the person rises 10 ft.
13. Find the work done by force field \(\vecs F(x,y,z)=−\dfrac{1}{2}x\,\hat{\mathbf i}−\dfrac{1}{2}y\,\hat{\mathbf j}+\dfrac{1}{4}\,\hat{\mathbf k}\) on a particle as it moves along the helix \(\vecs r(t)=\cos t\,\hat{\mathbf i}+\sin t\,\hat{\mathbf j}+t\,\hat{\mathbf k}\) from point \((1,0,0)\) to point \((−1,0,3π)\).
- Answer:
- \(W=\frac{3π}{4}\) units of work
14. Find the work done by vector field \(\vecs{F}(x,y)=y\,\hat{\mathbf i}+2x\,\hat{\mathbf j}\) in moving an object along path \(C\), which joins points \((1, 0)\) and \((0, 1)\).
15. Find the work done by force \(\vecs{F}(x,y)=2y\,\hat{\mathbf i}+3x\,\hat{\mathbf j}+(x+y)\,\hat{\mathbf k}\) in moving an object along curve \(\vecs r(t)=\cos(t)\,\hat{\mathbf i}+\sin(t)\,\hat{\mathbf j}+16\,\hat{\mathbf k}\), where \(0≤t≤2π\).
- Answer:
- \(W=π\) units of work
16. Find the mass of a wire in the shape of a circle of radius 2 centered at (3, 4) with linear mass density \(ρ(x,y)=y^2\).
For the following exercises, evaluate the line integrals.
17. Evaluate \(\displaystyle\int_C\vecs F·d\vecs{r}\), where \(\vecs{F}(x,y)=−1\,\hat{\mathbf j}\), and \(C\) is the part of the graph of \(y=12x^3−x\) from \((2,2)\) to \((−2,−2)\).
- Answer:
- \(\displaystyle\int _C\vecs F·d\vecs{r}=4\)
18. Evaluate \(\displaystyle\int _γ(x^2+y^2+z^2)^{−1}ds\), where \(γ\) is the helix \(x=\cos t,y=\sin t,z=t,\) with \(0≤t≤T.\)
19. Evaluate \(\displaystyle\int _Cyz\,dx+xz\,dy+xy\,dz\) over the line segment from \((1,1,1) \) to \((3,2,0).\)
- Answer:
- \(\displaystyle\int _Cyz\,dx+xz\,dy+xy\,dz=−1\)
20. Let \(C\) be the line segment from point (0, 1, 1) to point (2, 2, 3). Evaluate line integral \(\displaystyle\int _Cy\,ds.\)
21. [T] Use a computer algebra system to evaluate the line integral \(\displaystyle\int _Cy^2\,dx+x\,dy\), where \(C\) is the arc of the parabola \(x=4−y^2\) from \((−5, −3)\) to \((0, 2)\).
- Answer:
- \(\displaystyle\int _C(y^2)\,dx+(x)\,dy=\dfrac{245}{6}\)
22. [T] Use a computer algebra system to evaluate the line integral \(\displaystyle\int _C (x+3y^2)\,dy\) over the path \(C\) given by \(x=2t,y=10t,\) where \(0≤t≤1.\)
23. [T] Use a CAS to evaluate line integral \(\displaystyle\int _C xy\,dx+y\,dy\) over path \(C\) given by \(x=2t,y=10t\), where \(0≤t≤1\).
- Answer:
- \(\displaystyle\int _Cxy\,dx+y\,dy=\dfrac{190}{3}\)
24. Evaluate line integral \(\displaystyle\int _C(2x−y)\,dx+(x+3y)\,dy\), where \(C\) lies along the \(x\)-axis from \(x=0\) to \(x=5\).
26. [T] Use a CAS to evaluate \(\displaystyle\int _C\dfrac{y}{2x^2−y^2}\,ds\), where \(C\) is defined by the parametric equations \(x=t,y=t\), for \(1≤t≤5.\)
- Answer:
- \(\displaystyle\int _C\frac{y}{2x^2−y^2}\,ds=\sqrt{2}\ln 5\)
27. [T] Use a CAS to evaluate \(\displaystyle\int _Cxy\,ds\), where \(C\) is defined by the parametric equations \(x=t^2,y=4t\), for \(0≤t≤1.\)
In the following exercises, find the work done by force field \(\vecs F\) on an object moving along the indicated path.
28. \(\vecs{F}(x,y)=−x \,\hat{\mathbf i}−2y\,\hat{\mathbf j}\)
\(C:y=x^3\) from \((0, 0)\) to \((2, 8)\)
- Answer:
- \(W=−66\) units of work
29. \(\vecs{F}(x,y)=2x\,\hat{\mathbf i}+y\,\hat{\mathbf j}\)
<\(C\): counterclockwise around the triangle with vertices \((0, 0), (1, 0), \) and \((1, 1)\)
30. \(\vecs F(x,y,z)=x\,\hat{\mathbf i}+y\,\hat{\mathbf j}−5z\,\hat{\mathbf k}\)
\(C:\vecs r(t)=2\cos t\,\hat{\mathbf i}+2\sin t\,\hat{\mathbf j}+t\,\hat{\mathbf k},0≤t≤2π\)
- Answer:
- \(W=−10π^2\) units of work
31. Let \(\vecs F\) be vector field \(\vecs{F}(x,y)=(y^2+2xe^y+1)\,\hat{\mathbf i}+(2xy+x^2e^y+2y)\,\hat{\mathbf j}\). Compute the work of integral \(\displaystyle\int _C\vecs F·d\vecs{r}\), where \(C\) is the path \(\vecs r(t)=\sin t\,\hat{\mathbf i}+\cos t\,\hat{\mathbf j},\quad 0≤t≤\dfrac{π}{2}\).
32. Compute the work done by force \(\vecs F(x,y,z)=2x\,\hat{\mathbf i}+3y\,\hat{\mathbf j}−z\,\hat{\mathbf k}\) along path \(\vecs r(t)=t\,\hat{\mathbf i}+t^2\,\hat{\mathbf j}+t^3\,\hat{\mathbf k}\),where \(0≤t≤1\).
- Answer:
- \(W=2\) units of work
33. Evaluate \(\displaystyle\int _C\vecs F·d\vecs{r}\), where \(\vecs{F}(x,y)=\dfrac{1}{x+y}\,\hat{\mathbf i}+\dfrac{1}{x+y}\,\hat{\mathbf j}\) and \(C\) is the segment of the unit circle going counterclockwise from \((1,0)\) to \((0, 1)\).
34. Force \(\vecs F(x,y,z)=zy\,\hat{\mathbf i}+x\,\hat{\mathbf j}+z^2x\,\hat{\mathbf k}\) acts on a particle that travels from the origin to point \((1, 2, 3)\). Calculate the work done if the particle travels:
- along the path \((0,0,0)→(1,0,0)→(1,2,0)→(1,2,3)\) along straight-line segments joining each pair of endpoints;
- along the straight line joining the initial and final points.
- Is the work the same along the two paths?
- Answer:
- a. \(W=11\) units of work;
b. \(W=11\) units of work;
c. Yes
35. Find the work done by vector field \(\vecs F(x,y,z)=x\,\hat{\mathbf i}+3xy\,\hat{\mathbf j}−(x+z)\,\hat{\mathbf k}\) on a particle moving along a line segment that goes from \((1, 4, 2)\) to \((0, 5, 1).\)
36. How much work is required to move an object in vector field \(\vecs{F}(x,y)=y\,\hat{\mathbf i}+3x\,\hat{\mathbf j}\) along the upper part of ellipse \(\dfrac{x^2}{4}+y^2=1\) from \((2, 0)\) to \((−2,0)\)?
- Answer:
- \(W=2π\) units of work
37. A vector field is given by \(\vecs{F}(x,y)=(2x+3y)\,\hat{\mathbf i}+(3x+2y)\,\hat{\mathbf j}\). Evaluate the line integral of the field around a circle of unit radius traversed in a clockwise fashion.
38. Evaluate the line integral of scalar function \(xy\) along parabolic path \(y=x^2\) connecting the origin to point \((1, 1)\).
- Answer:
- \(\displaystyle\int _C f\,ds=\dfrac{25\sqrt{5}+1}{120}\)
39. Find \(\displaystyle\int _Cy^2\,dx+(xy−x^2)\,dy\) along \(C: y=3x\) from \((0, 0)\) to \((1, 3).\)
40. Find \(\displaystyle\int _Cy^2\,dx+(xy−x^2)\,dy\) along \(C: y^2=9x\) from \((0, 0)\) to \((1, 3).\)
- Answer:
- \(\displaystyle\int _Cy^2\,dx+(xy−x^2)\,dy=6.15\)
For the following exercises, use a CAS to evaluate the given line integrals.
41. [T] Evaluate \(\vecs F(x,y,z)=x^2z\,\hat{\mathbf i}+6y\,\hat{\mathbf j}+yz^2\,\hat{\mathbf k}\), where \(C\) is represented by \(\vecs r(t)=t\,\hat{\mathbf i}+t^2\,\hat{\mathbf j}+\ln t \,\hat{\mathbf k},1≤t≤3\).
42. [T] Evaluate line integral \(\displaystyle\int _γxe^y\,ds\) where, \(γ\) is the arc of curve \(x=e^y\) from \((1,0)\) to \((e,1)\).
- Answer:
- \(\displaystyle\int _γxe^y\,ds≈7.157\)
43. [T] Evaluate the integral \(\displaystyle\int _γxy^2\,ds\), where \(γ\) is a triangle with vertices \((0, 1, 2), (1, 0, 3)\), and \((0,−1,0)\).
44. [T] Evaluate line integral \(\displaystyle\int _γ(y^2−xy)\,dx\), where \(γ\) is curve \(y=\ln x\) from \((1, 0)\) toward \((e,1)\).
- Answer:
- \(\displaystyle\int _γ(y^2−xy)\,dx≈−1.379\)
45. [T] Evaluate line integral \(\displaystyle\int_γ xy^4\,ds\), where \(γ\) is the right half of circle \(x^2+y^2=16\).
46. [T] Evaluate \(\int C \vecs F⋅d\vecs{r},\int C \vecs F·d\vecs{r},\) where \(\vecs F(x,y,z)=x^2y\,\mathbf{\hat i}+(x−z)\,\mathbf{\hat j}+xyz\,\mathbf{\hat k}\) and
\(C: \vecs r(t)=t\,\mathbf{\hat i}+t^2\,\mathbf{\hat j}+2\,\mathbf{\hat k},0≤t≤1\).
- Answer:
- \(\displaystyle\int _C \vecs F⋅d\vecs{r}≈−1.133\) units of work
47. Evaluate \(\displaystyle\int _C \vecs F⋅d\vecs{r}\), where \(\vecs{F}(x,y)=2x\sin y\,\mathbf{\hat i}+(x^2\cos y−3y^2)\,\mathbf{\hat j}\) and
\(C\) is any path from \((−1,0)\) to \((5, 1)\).
48. Find the line integral of \(\vecs F(x,y,z)=12x^2\,\mathbf{\hat i}−5xy\,\mathbf{\hat j}+xz\,\mathbf{\hat k}\) over path \(C\) defined by \(y=x^2, z=x^3\) from point \((0, 0, 0)\) to point \((2, 4, 8)\).
- Answer:
- \(\displaystyle\int _C \vecs F⋅d\vecs{r}≈22.857\) units of work
49. Find the line integral of \(\displaystyle\int _C(1+x^2y)\,ds\), where \(C\) is ellipse \(\vecs r(t)=2\cos t\,\mathbf{\hat i}+3\sin t\,\mathbf{\hat j}\) from \(0≤t≤π.\)
For the following exercises, find the flux.
50. Compute the flux of \(\vecs{F}=x^2\,\mathbf{\hat i}+y\,\mathbf{\hat j}\) across a line segment from \((0, 0)\) to \((1, 2).\)
- Answer:
- \(\text{flux}=−\frac{1}{3}\)
51. Let \(\vecs{F}=5\,\mathbf{\hat i}\) and let \(C\) be curve \(y=0,\) with \(0≤x≤4\). Find the flux across \(C\).
52. Let \(\vecs{F}=5\,\mathbf{\hat j}\) and let \(C\) be curve \(y=0,\) with \(0≤x≤4\). Find the flux across \(C\).
- Answer:
- \(\text{flux}=-20\)
53. Let \(\vecs{F}=−y\,\mathbf{\hat i}+x\,\mathbf{\hat j}\) and let \(C: \vecs r(t)=\cos t\,\mathbf{\hat i}+\sin t\,\mathbf{\hat j}\) for \(0≤t≤2π\). Calculate the flux across \(C\).
54. Let \(\vecs{F}=(x^2+y^3)\,\mathbf{\hat i}+(2xy)\,\mathbf{\hat j}\). Calculate flux \(\vecs F\) orientated counterclockwise across the curve \(C: x^2+y^2=9.\)
- Answer:
- \(\text{flux}=0\)
Complete the rest of the exercises as stated.
55. Find the line integral of \(\displaystyle\int _C z^2\,dx+y\,dy+2y\,dz,\) where \(C\) consists of two parts: \(C_1\) and \(C_2.\) \(C_1\) is the intersection of cylinder \(x^2+y^2=16\) and plane \(z=3\) from \((0, 4, 3)\) to \((−4,0,3).\) \(C_2\) is a line segment from \((−4,0,3)\) to \((0, 1, 5)\).
56. A spring is made of a thin wire twisted into the shape of a circular helix \(x=2\cos t,\;y=2\sin t,\;z=t.\) Find the mass of two turns of the spring if the wire has a constant mass density of \(ρ\) grams per cm.
- Answer:
- \(m=4πρ\sqrt{5}\) grams
57. A thin wire is bent into the shape of a semicircle of radius \(a\). If the linear mass density at point \(P\) is directly proportional to its distance from the line through the endpoints, find the mass of the wire.
58. An object moves in force field \(\vecs F(x,y,z)=y^2\,\mathbf{\hat i}+2(x+1)y\,\mathbf{\hat j}\) counterclockwise from point \((2, 0)\) along elliptical path \(x^2+4y^2=4\) to \((−2,0)\), and back to point \((2, 0)\) along the \(x\)-axis. How much work is done by the force field on the object?
- Answer:
- \(W=0\) units of work
59. Find the work done when an object moves in force field \(\vecs F(x,y,z)=2x\,\mathbf{\hat i}−(x+z)\,\mathbf{\hat j}+(y−x)\,\mathbf{\hat k}\) along the path given by \(\vecs r(t)=t^2\,\mathbf{\hat i}+(t^2−t)\,\mathbf{\hat j}+3\,\mathbf{\hat k}, \; 0≤t≤1.\)
60. If an inverse force field \(\vecs F\) is given by \(\vecs F(x,y,z)=\dfrac{k}{‖r‖^3}r\), where \(k\) is a constant, find the work done by \(\vecs F\) as its point of application moves along the \(x\)-axis from \(A(1,0,0)\) to \(B(2,0,0)\).
- Answer:
- \(W=\frac{k}{2}\) units of work
61. David and Sandra plan to evaluate line integral \(\displaystyle\int _C\vecs F·d\vecs{r}\) along a path in the \(xy\)-plane from \((0, 0)\) to \((1, 1)\). The force field is \(\vecs{F}(x,y)=(x+2y)\,\mathbf{\hat i}+(−x+y^2)\,\mathbf{\hat j}\). David chooses the path that runs along the \(x\)-axis from \((0, 0)\) to \((1, 0)\) and then runs along the vertical line \(x=1\) from \((1, 0)\) to the final point \((1, 1)\). Sandra chooses the direct path along the diagonal line \(y=x\) from \((0, 0)\) to \((1, 1)\). Whose line integral is larger and by how much?
16.3: Conservative Vector Fields
1. True or False? If vector field \(\vecs F\) is conservative on the open and connected region \(D\), then line integrals of \(\vecs F\) are path independent on \(D\), regardless of the shape of \(D\).
- Answer:
- True
2. True or False? Function \(\vecs r(t)=\vecs a+t(\vecs b−\vecs a)\), where \(0≤t≤1\), parameterizes the straight-line segment from \(\vecs a\) to \(\vecs b\).
3. True or False? Vector field \(\vecs F(x,y,z)=(y\sin z)\,\mathbf{\hat i}+(x\sin z)\,\mathbf{\hat j}+(xy\cos z)\,\mathbf{\hat k}\) is conservative.
- Answer:
- True
4. True or False? Vector field \(\vecs F(x,y,z)=y\,\mathbf{\hat i}+(x+z)\,\mathbf{\hat j}−y\,\mathbf{\hat k}\) is conservative.
5. Justify the Fundamental Theorem of Line Integrals for \(\displaystyle \int _C\vecs F·d\vecs r\) in the case when \(\vecs{F}(x,y)=(2x+2y)\,\mathbf{\hat i}+(2x+2y)\,\mathbf{\hat j}\) and \(C\) is a portion of the positively oriented circle \(x^2+y^2=25\) from \((5, 0)\) to \((3, 4).\)
- Answer:
- \(\displaystyle \int _C \vecs F·d\vecs r=24\)
6. [T] Find \(\displaystyle \int _C\vecs F·d\vecs r,\) where \(\vecs{F}(x,y)=(ye^{xy}+\cos x)\,\mathbf{\hat i}+\left(xe^{xy}+\frac{1}{y^2+1}\right)\,\mathbf{\hat j}\) and \(C\) is a portion of curve \(y=\sin x\) from \(x=0\) to \(x=\frac{π}{2}\).
7. [T] Evaluate line integral \(\displaystyle \int _C\vecs F·d\vecs r\), where \(\vecs{F}(x,y)=(e^x\sin y−y)\,\mathbf{\hat i}+(e^x\cos y−x−2)\,\mathbf{\hat j}\), and \(C\) is the path given by \(\vecs r(t)=(t^3\sin\frac{πt}{2})\,\mathbf{\hat i}−(\frac{π}{2}\cos(\frac{πt}{2}+\frac{π}{2}))\,\mathbf{\hat j}\) for \(0≤t≤1\).
- Answer:
- \(\displaystyle \int _C\vecs F·d\vecs r=e−\dfrac{3π}{2}\)
For the following exercises, determine whether the vector field is conservative and, if it is, find the potential function.
8. \(\vecs{F}(x,y)=2xy^3\,\mathbf{\hat i}+3y^2x^2\,\mathbf{\hat j}\)
9. \(\vecs{F}(x,y)=(−y+e^x\sin y)\,\mathbf{\hat i}+((x+2)e^x\cos y)\,\mathbf{\hat j}\)
- Answer:
- Not conservative
10. \(\vecs{F}(x,y)=(e^{2x}\sin y)\,\mathbf{\hat i}+(e^{2x}\cos y)\,\mathbf{\hat j}\)
11. \(\vecs{F}(x,y)=(6x+5y)\,\mathbf{\hat i}+(5x+4y)\,\mathbf{\hat j}\)
- Answer:
- Conservative, \(f(x,y)=3x^2+5xy+2y^2\)
12. \(\vecs{F}(x,y)=(2x\cos(y)−y\cos(x))\,\mathbf{\hat i}+(−x^2\sin(y)−\sin(x))\,\mathbf{\hat j}\)
13. \(\vecs{F}(x,y)=(ye^x+\sin(y))\,\mathbf{\hat i}+(e^x+x\cos(y))\,\mathbf{\hat j}\)
- Answer:
- Conservative, \(f(x,y)=ye^x+x\sin(y)\)
For the following exercises, evaluate the line integrals using the Fundamental Theorem of Line Integrals.
14. \(\displaystyle ∮_C(y\,\mathbf{\hat i}+x\,\mathbf{\hat j})·d\vecs r,\) where \(C\) is any path from \((0, 0)\) to \((2, 4)\)
15. \(\displaystyle ∮_C(2y\,dx+2x\,dy),\) where \(C\) is the line segment from \((0, 0)\) to \((4, 4)\)
- Answer:
- \(\displaystyle ∮_C(2y\,dx+2x\,dy)=32\)
16. [T] \(∮_C\left[\arctan\dfrac{y}{x}−\dfrac{xy}{x^2+y^2}\right]\,dx+\left[\dfrac{x^2}{x^2+y^2}+e^{−y}(1−y)\right]\,dy\), where \(C\) is any smooth curve from \((1, 1)\) to \((−1,2).\)
17. Find the conservative vector field for the potential function \(\vecs{F}(x,y)=5x^2+3xy+10y^2.\)
- Answer:
- \(\vecs{F}(x,y)=(10x+3y)\,\mathbf{\hat i}+(3x+10y)\,\mathbf{\hat j}\)
For the following exercises, determine whether the vector field is conservative and, if so, find a potential function.
18. \(\vecs{F}(x,y)=(12xy)\,\mathbf{\hat i}+6(x^2+y^2)\,\mathbf{\hat j}\)
19. \(\vecs{F}(x,y)=(e^x\cos y)\,\mathbf{\hat i}+6(e^x\sin y)\,\mathbf{\hat j}\)
- Answer:
- \(\vecs F\) is not conservative.
20. \(\vecs{F}(x,y)=(2xye^{x^2y})\,\mathbf{\hat i}+6(x^2e^{x^2y})\,\mathbf{\hat j}\)
21. \(\vecs F(x,y,z)=(ye^z)\,\mathbf{\hat i}+(xe^z)\,\mathbf{\hat j}+(xye^z)\,\mathbf{\hat k}\)
- Answer:
- \(\vecs F\) is conservative and a potential function is \(f(x,y,z)=xye^z\).
22. \(\vecs F(x,y,z)=(\sin y)\,\mathbf{\hat i}−(x\cos y)\,\mathbf{\hat j}+\,\mathbf{\hat k}\)
23. \(\vecs F(x,y,z)=\left(\frac{1}{y}\right)\,\mathbf{\hat i}+(\frac{x}{y^2})\,\mathbf{\hat j}+(2z−1)\,\mathbf{\hat k}\)
- Answer:
- \(\vecs F\) is conservative and a potential function is \(f(x,y,z)=z.\)
24. \(\vecs F(x,y,z)=3z^2\,\mathbf{\hat i}−\cos y\,\mathbf{\hat j}+2xz\,\mathbf{\hat k}\)
25. \(\vecs F(x,y,z)=(2xy)\,\mathbf{\hat i}+(x^2+2yz)\,\mathbf{\hat j}+y^2\,\mathbf{\hat k}\)
- Answer:
- \(\vecs F\) is conservative and a potential function is \(f(x,y,z)=x^2y+y^2z.\)
For the following exercises, determine whether the given vector field is conservative and find a potential function.
26. \(\vecs{F}(x,y)=(e^x\cos y)\,\mathbf{\hat i}+6(e^x\sin y)\,\mathbf{\hat j}\)
27. \(\vecs{F}(x,y)=(2xye^{x^2y})\,\mathbf{\hat i}+6(x^2e^{x^2y})\,\mathbf{\hat j}\)
- Answer:
- \(\vecs F\) is conservative and a potential function is \(\vecs{F}(x,y)=e^{x^2y}\)
For the following exercises, evaluate the integral using the Fundamental Theorem of Line Integrals.
28. Evaluate \(\displaystyle \int _C\vecs ∇f·d\vecs r\), where \(f(x,y,z)=\cos(πx)+\sin(πy)−xyz\) and \(C\) is any path that starts at \((1,12,2)\) and ends at \((2,1,−1)\).
29. [T] Evaluate \(\displaystyle \int _C\vecs ∇f·d\vecs r\), where \(\vecs{F}(x,y)=xy+e^x\) and \(C\) is a straight line from \((0,0)\) to \((2,1)\).
- Answer:
- \(\displaystyle \int _C\vecs F·d\vecs r=e^2+1\)
30. [T] Evaluate \(\displaystyle \int _C\vecs ∇f·d\vecs r,\) where \(\vecs{F}(x,y)=x^2y−x\) and \(C\) is any path in a plane from (1, 2) to (3, 2).
31. Evaluate \(\displaystyle \int _C\vecs ∇f·d\vecs r,\) where \(f(x,y,z)=xyz^2−yz\) and \(C\) has initial point (1, 2) and terminal point (3, 5).
- Answer:
- \(\displaystyle \int _C\vecs F·d\vecs r=41\)
For the following exercises, let \(\vecs{F}(x,y)=2xy^2\,\mathbf{\hat i}+(2yx^2+2y)\,\mathbf{\hat j}\) and \(G(x,y)=(y+x)\,\mathbf{\hat i}+(y−x)\,\mathbf{\hat j}\), and let \(C_1\) be the curve consisting of the circle of radius 2, centered at the origin and oriented counterclockwise, and\(C_2\) be the curve consisting of a line segment from \((0, 0)\) to \((1, 1)\) followed by a line segment from \((1, 1)\) to \((3, 1).\)
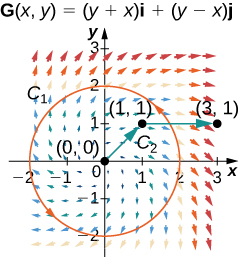
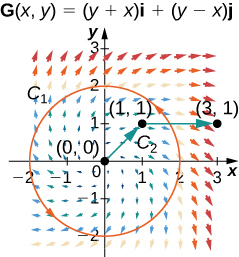
32. Calculate the line integral of \(\vecs F\) over \(C_1\).
33. Calculate the line integral of \(\vecs G\) over \(C_1\).
- Answer:
- \(\displaystyle ∮_{C_1}\vecs G·d\vecs r=−8π\)
34. Calculate the line integral of \(\vecs F\) over \(C_2\).
35. Calculate the line integral of \(\vecs G\) over \(C_2\).
- Answer:
- \(\displaystyle ∮_{C_2}\vecs F·d\vecs r=7\)
36. [T] Let \(\vecs F(x,y,z)=x^2\,\mathbf{\hat i}+z\sin(yz)\,\mathbf{\hat j}+y\sin(yz)\,\mathbf{\hat k}\). Calculate \(\displaystyle ∮_C\vecs F·d\vecs{r}\), where \(C\) is a path from \(A=(0,0,1)\) to \(B=(3,1,2)\).
37. [T] Find line integral \(\displaystyle ∮_C\vecs F·dr\) of vector field \(\vecs F(x,y,z)=3x^2z\,\mathbf{\hat i}+z^2\,\mathbf{\hat j}+(x^3+2yz)\,\mathbf{\hat k}\) along curve \(C\) parameterized by \(\vecs r(t)=(\frac{\ln t}{\ln 2})\,\mathbf{\hat i}+t^{3/2}\,\mathbf{\hat j}+tcos(πt),1≤t≤4.\)
- Answer:
- \(\displaystyle \int _C\vecs F·d\vecs r=150\)
For the following exercises, show that the following vector fields are conservative by using a computer. Calculate \(\displaystyle \int _C\vecs F·d\vecs r\) for the given curve.
38. \(\vecs{F}(x,y)=(xy^2+3x^2y)\,\mathbf{\hat i}+(x+y)x^2\,\mathbf{\hat j}\); \(C\) is the curve consisting of line segments from \((1,1)\) to \((0,2)\) to \((3,0).\)
39. \(\vecs{F}(x,y)=\dfrac{2x}{y^2+1}\,\mathbf{\hat i}−\dfrac{2y(x^2+1)}{(y^2+1)^2}\,\mathbf{\hat j}\); \(C\) is parameterized by ](x=t^3−1,y=t^6−t,0≤t≤1.\)
- Answer:
- \(\displaystyle \int _C\vecs F·d\vecs r=−1\)
40. [T] \(\vecs{F}=[\cos(xy^2)−xy^2\sin(xy^2)]\,\mathbf{\hat i}−2x^2y\sin(xy^2)\,\mathbf{\hat j}\); \(C\) is curve \(\langle e^t,e^{t+1}\rangle,−1≤t≤0\).
41. The mass of Earth is approximately \(6×10^{27}g\) and that of the Sun is 330,000 times as much. The gravitational constant is \(6.7×10^{−8}cm^3/s^2·g\). The distance of Earth from the Sun is about \(1.5×10^{12}cm\). Compute, approximately, the work necessary to increase the distance of Earth from the Sun by 1cm.
- Answer:
- \(4×10^{31}\) erg
42. [T] Let \(\vecs{F}(x,y,z)=(e^x\sin y)\,\mathbf{\hat i}+(e^x\cos y)\,\mathbf{\hat j}+z^2\,\mathbf{\hat k}\). Evaluate the integral \(\displaystyle \int _C\vecs F·ds\), where \(\vecs c(t)=(\sqrt{t},t^3,e^{\sqrt{t}}),\;0≤t≤1.\)
43. [T] Let \(\vecs c:[1,2]→ℝ^2\) be given by \(x=e^{t−1},y=\sin\left(\frac{π}{t}\right)\). Use a computer to compute the integral \(\displaystyle \int _C\vecs F·d\vecs s=\int _C 2x\cos y\,dx−x^2\sin y\,dy\), where \(\vecs{F}(x,y)=(2x\cos y)\,\mathbf{\hat i}−(x^2\sin y)\,\mathbf{\hat j}.\)
- Answer:
- \(\displaystyle \int _C\vecs F·d\vecs s=0.4687\)
44. [T] Use a computer algebra system to find the mass of a wire that lies along curve \(\vecs r(t)=(t^2−1)\,\mathbf{\hat j}+2t\,\mathbf{\hat k},\;0≤t≤1\), if the density is \(\dfrac{3}{2}t\).
45. Find the circulation and flux of field \(\vecs{F}(x,y)=−y\,\mathbf{\hat i}+x\,\mathbf{\hat j}\) around and across the closed semicircular path that consists of semicircular arch \(\vecs r_1(t)=(a\cos t)\,\mathbf{\hat i}+(a\sin t)\,\mathbf{\hat j},\quad 0≤t≤π\), followed by line segment \(\vecs r_2(t)=t\,\mathbf{\hat i},\quad −a≤t≤a.\)
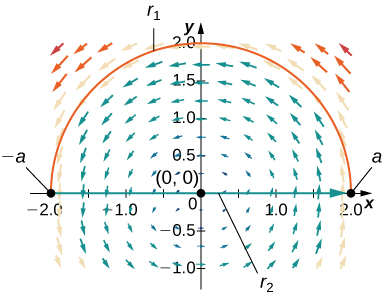
- Answer:
- \(\text{circulation}=πa^2\) and \(\text{flux}=0\)
46. Compute \(\displaystyle \int _C\cos x\cos y\,dx−\sin x\sin y\,dy,\) where \(\vecs c(t)=\langle t,t^2 \rangle, \quad 0≤t≤1.\)
47. Complete the proof of the theorem titled THE PATH INDEPENDENCE TEST FOR CONSERVATIVE FIELDS by showing that \(f_y=Q(x,y).\)
16.4: Green’s Theorem
For the following exercises, evaluate the line integrals by applying Green’s theorem.
1. \(\displaystyle \int_C 2xy\,dx+(x+y)\,dy\), where \(C\) is the path from \((0, 0)\) to \((1, 1)\) along the graph of \(y=x^3\) and from \((1, 1)\) to \((0, 0)\) along the graph of \(y=x\) oriented in the counterclockwise direction
2. \(\displaystyle \int_C 2xy\,dx+(x+y)\,dy\), where \(C\) is the boundary of the region lying between the graphs of \(y=0\) and \(y=4−x^2\) oriented in the counterclockwise direction
- Answer:
- \(\displaystyle \int_C2xy\,dx+(x+y)\,dy=\frac{32}{3}\)
3. \(\displaystyle \int_C 2\arctan\left(\frac{y}{x}\right)\,dx+\ln(x^2+y^2)\,dy\), where \(C\) is defined by \(x=4+2\cos θ,\;y=4\sin θ\) oriented in the counterclockwise direction
4. \(\displaystyle \int_C \sin x\cos y\,dx+(xy+\cos x\sin y)\,dy\), where \(C\) is the boundary of the region lying between the graphs of \(y=x\) and \(y=\sqrt{x}\) oriented in the counterclockwise direction
- Answer:
- \(\displaystyle \int_C\sin x\cos y\,dx+(xy+\cos x\sin y)\,dy=\frac{1}{12}\)
5. \(\displaystyle \int_C xy\,dx+(x+y)\,dy\), where \(C\) is the boundary of the region lying between the graphs of \(x^2+y^2=1\) and \(x^2+y^2=9\) oriented in the counterclockwise direction
6. \(\displaystyle ∮_C (−y\,dx+x\,dy)\), where \(C\) consists of line segment \(C_1\) from \((−1,0)\) to \((1, 0)\), followed by the semicircular arc \(C_2\) from \((1, 0)\) back to \((1, 0)\)
- Answer:
- \(\displaystyle ∮_C (−y\,\,dx+x\,\,dy)=π\)
For the following exercises, use Green’s theorem.
7. Let \(C\) be the curve consisting of line segments from \((0, 0)\) to \((1, 1)\) to \((0, 1)\) and back to \((0, 0)\). Find the value of \(\displaystyle \int_C xy\,dx+\sqrt{y^2+1}\,dy\).
8. Evaluate line integral \(\displaystyle \int_C xe^{−2x}\,dx+(x^4+2x^2y^2)\,dy\), where \(C\) is the boundary of the region between circles \(x^2+y^2=1\) and \(x^2+y^2=4\), and is a positively oriented curve.
- Answer:
- \(\displaystyle \int_C xe^{−2x}\,dx+(x^4+2x^2y^2)\,dy=0\)
9. Find the counterclockwise circulation of field \(\vecs F(x,y)=xy\,\mathbf{\hat i}+y^2\,\mathbf{\hat j}\) around and over the boundary of the region enclosed by curves \(y=x^2\) and \(y=x\) in the first quadrant and oriented in the counterclockwise direction.
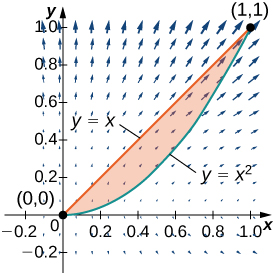
10. Evaluate \(\displaystyle ∮_C y^3\,dx−x^3y^2\,dy\), where \(C\) is the positively oriented circle of radius \(2\) centered at the origin.
- Answer:
- \(\displaystyle ∮_C y^3\,dx−x^3y^2\,dy=−24π\)
11. Evaluate \(\displaystyle ∮_C y^3\,dx−x^3\,dy\), where \(C\) includes the two circles of radius \(2\) and radius \(1\) centered at the origin, both with positive orientation.
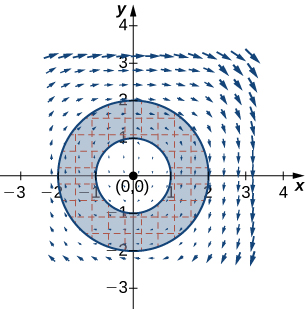
12. Calculate \(\displaystyle ∮_C −x^2y\,dx+xy^2\,dy\), where \(C\) is a circle of radius \(2\) centered at the origin and oriented in the counterclockwise direction.
- Answer:
- \(\displaystyle ∮_C −x^2y\,dx+xy^2\,dy=8π\)
13. Calculate integral \(\displaystyle ∮_C 2[y+x\sin(y)]\,dx+[x^2\cos(y)−3y^2]\,dy\) along triangle \(C\) with vertices \((0, 0), \,(1, 0)\) and \((1, 1)\), oriented counterclockwise, using Green’s theorem.
14. Evaluate integral \(\displaystyle ∮_C (x^2+y^2)\,dx+2xy\,dy\), where \(C\) is the curve that follows parabola \(y=x^2\) from \((0,0), \,(2,4),\) then the line from \((2, 4)\) to \((2, 0)\), and finally the line from \((2, 0)\) to \((0, 0)\).
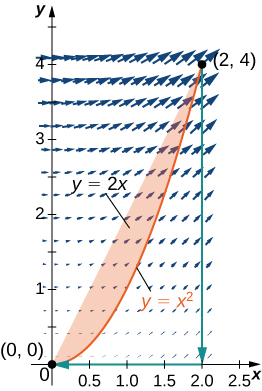
- Answer:
- \(\displaystyle ∮_C (x^2+y^2)\,dx+2xy\,dy=0\)
15. Evaluate line integral \(\displaystyle ∮_C (y−\sin(y)\cos(y))\,dx+2x\sin^2(y)\,dy\), where \(C\) is oriented in a counterclockwise path around the region bounded by \(x=−1, \,x=2, \,y=4−x^2\), and \(y=x−2.\)
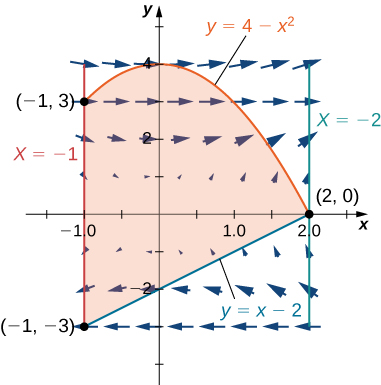
For the following exercises, use Green’s theorem to find the area.
16. Find the area between ellipse \(\frac{x^2}{9}+\frac{y^2}{4}=1\) and circle \(x^2+y^2=25\).
- Answer:
- \(A=19π\;\text{units}^2\)
17. Find the area of the region enclosed by parametric equation
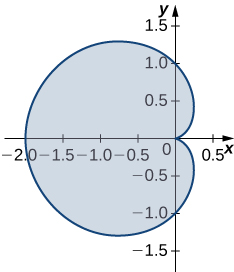
\(\vecs p(θ)=(\cos(θ)−\cos^2(θ))\,\mathbf{\hat i}+(\sin(θ)−\cos(θ)\sin(θ))\,\mathbf{\hat j}\) for \(0≤θ≤2π.\)
18. Find the area of the region bounded by hypocycloid \(\vecs r(t)=\cos^3(t)\,\mathbf{\hat i}+\sin^3(t)\,\mathbf{\hat j}\). The curve is parameterized by \(t∈[0,2π].\)
- Answer:
- \(A=\frac{3}{8π}\;\text{units}^2\)
19. Find the area of a pentagon with vertices \((0,4), \,(4,1), \,(3,0), \,(−1,−1),\) and \((−2,2)\).
20. Use Green’s theorem to evaluate \(\displaystyle \int_{C^+}(y^2+x^3)\,dx+x^4\,dy\), where \(C^+\) is the perimeter of square \([0,1]×[0,1]\) oriented counterclockwise.
- Answer:
- \(\displaystyle \int_{C^+} (y^2+x^3)\,dx+x^4\,dy=0\)
21. Use Green’s theorem to prove the area of a disk with radius \(a\) is \(A=πa^2\;\text{units}^2\).
22. Use Green’s theorem to find the area of one loop of a four-leaf rose \(r=3\sin 2θ\). (Hint: \(x\,dy−y\,dx=r^2\,dθ\)).
- Answer:
- \(A=\frac{9π}{8}\;\text{units}^2\)
23. Use Green’s theorem to find the area under one arch of the cycloid given by the parametric equations: \(x=t−\sin t,\;y=1−\cos t,\;t≥0.\)
24. Use Green’s theorem to find the area of the region enclosed by curve
\(\vecs r(t)=t^2\,\mathbf{\hat i}+\left(\frac{t^3}{3}−t\right)\,\mathbf{\hat j},\) for \(−\sqrt{3}≤t≤\sqrt{3}\).
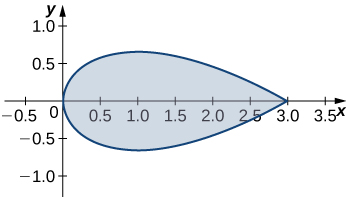
- Answer:
- \(A=\frac{8\sqrt{3}}{5}\;\text{units}^2\)
25. [T] Evaluate Green’s theorem using a computer algebra system to evaluate the integral \(\displaystyle \int_C xe^y\,dx+e^x\,dy\), where \(C\) is the circle given by \(x^2+y^2=4\) and is oriented in the counterclockwise direction.
26. Evaluate \(\displaystyle \int_C(x^2y−2xy+y^2)\,ds\), where \(C\) is the boundary of the unit square \(0≤x≤1,\;0≤y≤1\), traversed counterclockwise.
- Answer:
- \(\displaystyle \int_C (x^2y−2xy+y^2)\,ds=3\)
27. Evaluate \(\displaystyle \int_C \frac{−(y+2)\,dx+(x−1)\,dy}{(x−1)^2+(y+2)^2}\), where \(C\) is any simple closed curve with an interior that does not contain point \((1,−2)\) traversed counterclockwise.
28. Evaluate \(\displaystyle \int_C \frac{x\,dx+y\,dy}{x^2+y^2}\), where \(C\) is any piecewise, smooth simple closed curve enclosing the origin, traversed counterclockwise.
- Answer:
- \(\displaystyle \int_C \frac{x\,dx+y\,dy}{x^2+y^2}=2π\)
For the following exercises, use Green’s theorem to calculate the work done by force \(\vecs F\) on a particle that is moving counterclockwise around closed path \(C\).
29. \(\vecs F(x,y)=xy\,\mathbf{\hat i}+(x+y)\,\mathbf{\hat j}, \quad C:x^2+y^2=4\)
30. \(\vecs F(x,y)=(x^{3/2}−3y)\,\mathbf{\hat i}+(6x+5\sqrt{y})\,\mathbf{\hat j}, \quad C\): boundary of a triangle with vertices \((0, 0), \,(5, 0),\) and \((0, 5)\)
- Answer:
- \(W=\frac{225}{2}\) units of work
31. Evaluate \(\displaystyle \int_C (2x^3−y^3)\,dx+(x^3+y^3)\,dy\), where \(C\) is a unit circle oriented in the counterclockwise direction.
32. A particle starts at point \((−2,0)\), moves along the \(x\)-axis to \((2, 0)\), and then travels along semicircle \(y=\sqrt{4−x^2}\) to the starting point. Use Green’s theorem to find the work done on this particle by force field \(\vecs F(x,y)=x\,\mathbf{\hat i}+(x^3+3xy^2)\,\mathbf{\hat j}\).
- Answer:
- \(W=12π\) units of work
33. David and Sandra are skating on a frictionless pond in the wind. David skates on the inside, going along a circle of radius \(2\) in a counterclockwise direction. Sandra skates once around a circle of radius \(3\), also in the counterclockwise direction. Suppose the force of the wind at point \((x,y)\) is \(\vecs F(x,y)=(x^2y+10y)\,\mathbf{\hat i}+(x^3+2xy^2)\,\mathbf{\hat j}\). Use Green’s theorem to determine who does more work.
34. Use Green’s theorem to find the work done by force field \(\vecs F(x,y)=(3y−4x)\,\mathbf{\hat i}+(4x−y)\,\mathbf{\hat j}\) when an object moves once counterclockwise around ellipse \(4x^2+y^2=4.\)
- Answer:
- \(W=2π\) units of work
35. Use Green’s theorem to evaluate line integral \(\displaystyle ∮_C e^{2x}\sin 2y\,dx+e^{2x}\cos 2y\,dy\), where \(C\) is ellipse \(9(x−1)^2+4(y−3)^2=36\) oriented counterclockwise.
36. Evaluate line integral \(\displaystyle ∮_C y^2\,dx+x^2\,dy\), where \(C\) is the boundary of a triangle with vertices \((0,0), \,(1,1)\), and \((1,0)\), with the counterclockwise orientation.
- Answer:
- \(\displaystyle ∮_C y^2\,dx+x^2\,dy=\frac{1}{3}\)
37. Use Green’s theorem to evaluate line integral \(\displaystyle \int_C \vecs h·d\vecs r\) if \(\vecs h(x,y)=e^y\,\mathbf{\hat i}−\sin πx\,\mathbf{\hat j}\), where \(C\) is a triangle with vertices \((1, 0), \,(0, 1),\) and \((−1,0),\) traversed counterclockwise.
38. Use Green’s theorem to evaluate line integral \(\displaystyle \int_C\sqrt{1+x^3}\,dx+2xy\,dy\) where \(C\) is a triangle with vertices \((0, 0), \,(1, 0),\) and \((1, 3)\) oriented clockwise.
- Answer:
- \(\displaystyle \int_C \sqrt{1+x^3}\,dx+2xy\,dy=3\)
39. Use Green’s theorem to evaluate line integral \(\displaystyle \int_C x^2y\,dx−xy^2\,dy\) where \(C\) is a circle \(x^2+y^2=4\) oriented counterclockwise.
40. Use Green’s theorem to evaluate line integral \(\displaystyle \int_C \left(3y−e^{\sin x}\right)\,dx+\left(7x+\sqrt{y^4+1}\right)\,dy\) where \(C\) is circle \(x^2+y^2=9\) oriented in the counterclockwise direction.
- Answer:
- \(\displaystyle \int_C \left(3y−e^{\sin x}\right)\,dx+\left(7x+\sqrt{y^4+1}\right)\,dy=36π\)
41. Use Green’s theorem to evaluate line integral \(\displaystyle \int_C (3x−5y)\,dx+(x−6y)\,dy\), where \(C\) is ellipse \(\frac{x^2}{4}+y^2=1\) and is oriented in the counterclockwise direction.

42. Let \(C\) be a triangular closed curve from \((0, 0)\) to \((1, 0)\) to \((1, 1)\) and finally back to \((0, 0).\) Let \(\vecs F(x,y)=4y\,\mathbf{\hat i}+6x^2\,\mathbf{\hat j}.\) Use Green’s theorem to evaluate \(\displaystyle ∮_C\vecs F·d\vecs r.\)
- Answer:
- \(\displaystyle ∮_C\vecs F·d\vecs r=2\)
43. Use Green’s theorem to evaluate line integral \(\displaystyle ∮_C y\,dx−x\,dy\), where \(C\) is circle \(x^2+y^2=a^2\) oriented in the clockwise direction.
44. Use Green’s theorem to evaluate line integral \(\displaystyle ∮_C (y+x)\,dx+(x+\sin y)\,dy,\) where \(C\) is any smooth simple closed curve joining the origin to itself oriented in the counterclockwise direction.
- Answer:
- \(\displaystyle ∮_C (y+x)\,dx+(x+\sin y)\,dy=0\)
45. Use Green’s theorem to evaluate line integral \(\displaystyle ∮_C \left(y−\ln(x^2+y^2)\right)\,dx+\left(2\arctan \frac{y}{x}\right)\,dy,\) where \(C\) is the positively oriented circle \((x−2)^2+(y−3)^2=1.\)
46. Use Green’s theorem to evaluate \(\displaystyle ∮_C xy\,dx+x^3y^3\,dy,\) where \(C\) is a triangle with vertices \((0, 0), \,(1, 0),\) and \((1, 2)\) with positive orientation.
- Answer:
- \(\displaystyle ∮_C xy\,dx+x^3y^3\,dy=2221\)
47. Use Green’s theorem to evaluate line integral \(\displaystyle \int_C \sin y\,dx+x\cos y\,dy,\) where \(C\) is ellipse \(x^2+xy+y^2=1\) oriented in the counterclockwise direction.
48. Let \(\vecs F(x,y)=\left(\cos(x^5)−13y^3\right)\,\mathbf{\hat i}+13x^3\,\mathbf{\hat j}.\) Find the counterclockwise circulation \(\displaystyle ∮_C\vecs F·d\vecs r,\) where \(C\) is a curve consisting of the line segment joining \((−2,0)\) and \((−1,0),\) half circle \(y=\sqrt{1−x^2},\) the line segment joining \((1, 0)\) and \((2, 0),\) and half circle \(y=\sqrt{4−x^2}.\)
- Answer:
- \(\displaystyle ∮_C\vecs F·d\vecs r=15π^4\)
49. Use Green’s theorem to evaluate line integral \(\displaystyle ∫_C \sin(x^3)\,dx+2ye^{x^2}\,dy,\) where \(C\) is a triangular closed curve that connects the points \((0, 0), \,(2, 2),\) and \((0, 2)\) counterclockwise.
50. Let \(C\) be the boundary of square \(0≤x≤π,\;0≤y≤π,\) traversed counterclockwise. Use Green’s theorem to find \(\displaystyle ∫_C \sin(x+y)\,dx+\cos(x+y)\,dy.\)
- Answer:
- \(\displaystyle \int_C\sin(x+y)\,dx+\cos(x+y)\,dy=4\)
51. Use Green’s theorem to evaluate line integral \(\displaystyle ∫_C \vecs F·d\vecs r,\) where \(\vecs F(x,y)=(y^2−x^2)\,\mathbf{\hat i}+(x^2+y^2)\,\mathbf{\hat j},\) and \(C\) is a triangle bounded by \(y=0,\;x=3,\) and \(y=x,\) oriented counterclockwise.
52. Use Green’s Theorem to evaluate integral \(\displaystyle ∫_C \vecs F·d\vecs r,\) where \(\vecs F(x,y)=(xy^2)\,\mathbf{\hat i}+x\,\mathbf{\hat j},\) and \(C\) is a unit circle oriented in the counterclockwise direction.
- Answer:
- \(\displaystyle ∫_C \vecs F·d\vecs r=π\)
53. Use Green’s theorem in a plane to evaluate line integral \(\displaystyle ∮_C (xy+y^2)\,dx+x^2\,dy,\) where \(C\) is a closed curve of a region bounded by \(y=x\) and \(y=x^2\) oriented in the counterclockwise direction.
54. Calculate the outward flux of \(\vecs F(x,y)=−x\,\mathbf{\hat i}+2y\,\mathbf{\hat j}\) over a square with corners \((±1,\,±1),\) where the unit normal is outward pointing and oriented in the counterclockwise direction.
- Answer:
- \(\displaystyle ∮_C\vecs F·\vecs N \,ds=4\)
55. [T] Let \(C\) be circle \(x^2+y^2=4\) oriented in the counterclockwise direction. Evaluate \(\displaystyle ∮_C \left[\left(3y−e^{\arctan x})\,dx+(7x+\sqrt{y^4+1}\right)\,dy\right]\) using a computer algebra system.
56. Find the flux of field \(\vecs F(x,y)=−x\,\mathbf{\hat i}+y\,\mathbf{\hat j}\) across \(x^2+y^2=16\) oriented in the counterclockwise direction.
- Answer:
- \(\displaystyle ∮_C \vecs F·\vecs N\,ds=32π\)
57. Let \(\vecs F=(y^2−x^2)\,\mathbf{\hat i}+(x^2+y^2)\,\mathbf{\hat j},\) and let \(C\) be a triangle bounded by \(y=0, \,x=3,\) and \(y=x\) oriented in the counterclockwise direction. Find the outward flux of \(\vecs F\) through \(C\).
58. [T] Let \(C\) be unit circle \(x^2+y^2=1\) traversed once counterclockwise. Evaluate \(\displaystyle ∫_C \left[−y^3+\sin(xy)+xy\cos(xy)\right]\,dx+\left[x^3+x^2\cos(xy)\right]\,dy\) by using a computer algebra system.
- Answer:
- \(\displaystyle ∫_C \left[−y^3+\sin(xy)+xy\cos(xy)\right]\,dx+\left[x^3+x^2\cos(xy)\right]\,dy=4.7124\)
59. [T] Find the outward flux of vector field \(\vecs F(x,y)=xy^2\,\mathbf{\hat i}+x^2y\,\mathbf{\hat j}\) across the boundary of annulus \(R=\big\{(x,y):1≤x^2+y^2≤4\big\}=\big\{(r,θ):1≤r≤2,\,0≤θ≤2π\big\}\) using a computer algebra system.
60. Consider region \(R\) bounded by parabolas \(y=x^2\) and \(x=y^2.\) Let \(C\) be the boundary of \(R\) oriented counterclockwise. Use Green’s theorem to evaluate \(\displaystyle ∮_C \left(y+e^{\sqrt{x}}\right)\,dx+\left(2x+\cos(y^2)\right)\,dy.\)
- Answer:
- \(\displaystyle ∮_C \left(y+e^{\sqrt{x}}\right)\,dx+\left(2x+\cos(y^2)\right)\,dy=13\)
16.5: Divergence and Curl
For the following exercises, determine whether the statement is true or false.
If the coordinate functions of \(F : \mathbb{R}^3 \rightarrow \mathbb{R}^3\) have continuous second partial derivatives, then \(curl \, (div (F))\) equals zero.
\(\nabla \cdot (xi + yj + zk) = 1\).
[Hide Solution]
False
All vector fields of the form
\(F(x,y,z) = f(x)i + g(y)j + h(z)k\) are conservative.
If \(curl \, F = 0\), then F is conservative.
[Hide Solution]
True
If F is a constant vector field then \(div \, F = 0\).
If F is a constant vector field then \(curl \, F = 0\).
[Hide Solution]
True
For the following exercises, find the curl of F.
\(F(x,y,z) = xy^2z^4 i + (2x^2y + z)j + y^3 z^2 k\)
\(F(x,y,z) = x^2 zi + y^2 xj + (y + 2z) k\)
[Hide Solution]
\(curl \, F = i + x^2 j + y^2 k\)
\(F(x,y,z) = 3xyz^2i + y^2 \sin z j + xe^{2z} k\)
\(F(x,y,z) = x^2 yzi + xy^2 zj + xyz^2 k\)
[Hide Solution]
\(curl \, F = (xz^2 - xy^2)i + (x^2 y - yz^2)j + (y^2z - x^2z) k\)
\(F(x,y,z) = (x \, \cos y)i + xy^2j\)
\(F(x,y,z) = (x - y)i + (y - z)j + (z - x) k\)
[Hide Solution]
\(curl \, F = i + j + k\)
\(F(x,y,z) = xyzi + x^2y^2z^2j + y^2z^3k\)
\(F(x,y,z) = xyi + yzj + xz k\)
[Hide Solution]
\(curl \, F = - yi - zj - xk\)
\(F(x,y,z) = x^2 i + y^2 j + z^2 k\)
\(F(x,y,z) = axi + byj + c k\) for constants a, b, c
[Hide Solution]
\(curl \, F = 0\)
For the following exercises, find the divergence of F.
\(F(x,y,z) = x^2 z i + y^2 x j + (y + 2z) k\)
\(F(x,y,z) = 3xyz^2 i + y^2 \sin z j + xe^2 k\)
[Hide Solution]
\(div F = 3yz^2 + 2y \, \sin z + 2xe^{2z}\)
\(\vecs{F}(x,y) = (\sin x) i + (\cos y) j\)
\(F(x,y,z) = x^2 i + y^2 j + z^2 k\)
[Hide Solution]
\(div \, F = 2(x + y + z)\)
\(F(x,y,z) = (x - y) i + (y - z) j + (z - x) k\)
\(\vecs{F}(x,y) = \dfrac{x}{\sqrt{x^2+y^2}}i + \dfrac{y}{\sqrt{x^2+y^2}}j\)
[Hide Solution]
\(div \, F = \dfrac{1}{\sqrt{x^2+y^2}}\)
\(\vecs{F}(x,y) = xi - yj\)
\(F(x,y,z) = axi + byj + ck\) for constants a, b, c
[ Hide Solution]
\(div \, F = a + b\)
\(F(x,y,z) = xyzi + x^2y^2z^2j + y^2z^3k\)
\(F(x,y,z) = xyi + yzj + xzk\)
[Hide Solution]
\(div \, F = x + y + z\)
For the following exercises, determine whether each of the given scalar functions is harmonic.
\(u(x,y,z) = e^{-x} (\cos y - \sin y)\)
\(w(x,y,z) = (x^2 + y^2 + z^2)^{-1/2}\)
[Hide Solution]
Harmonic
If \(F(x,y,z) = 2 i + 2x j + 3y k\) and
\(G(x,y,z) = x i - y j + z k\), find \(curl \, (F \times G)\).
If \(F(x,y,z) = 2 i + 2x j + 3y k\) and
\(G(x,y,z) = x i - y j + z k\), find \(div \, (F \times G)\).
[Hide Solution]
\(div \, (F \times G) = 2z + 3x\)
Find \(div \, F\), given that \(F = \nabla f\), where \(f(x,y,z) = xy^3z^2\).
Find the divergence of F for vector field
\(F(x,y,z) = (y^2 + z^2) (x + y) i + (z^2 + x^2)(y + z) j + (x^2 + y^2)(z + x) k\).
[Hide Solution]
\(div \, F = 2r^2\)
Find the divergence of F for vector field
\(F(x,y,z) = f_1(y,z) i + f_2 (x,z) j + f_3 (x,y) k\).
For the following exercises, use \(r = |r|\) and \(r = (x,y,z)\).
Find the \(curl \, r\)
[Hide Solution]
\(curl \, r = 0\)
Find the \(curl \, \dfrac{r}{r}\).
Find the \(curl \, \dfrac{r}{r^3}\).
[Hide Solution]
\(curl \, \dfrac{r}{r^3} = 0\)
Let \(\vecs{F}(x,y) = \dfrac{-yi+xj}{x^2+y^2}\), where F is defined on \(\{(x,y) \in \mathbb{R} | (x,y) \neq (0,0) \}\). Find \(curl \, F\).
For the following exercises, use a computer algebra system to find the curl of the given vector fields.
[T] \(F(x,y,z) = arctan \left(\dfrac{x}{y}\right) i + \ln \sqrt{x^2 + y^2} j + k\)
[Hide Solution]
\(curl \, F = \dfrac{2x}{x^2+y^2} k\)
[T]
\(F(x,y,z) = \sin (x - y) i + \sin (y - z) j + \sin (z - x) k\)
For the following exercises, find the divergence of F at the given point.
\(F(x,y,z) = i + j + k\) at \((2, -1, 3)\)
[Hide Solution]
\(div \, F = 0\)
\(F(x,y,z) = xyz i + y j + zk\) at \((1, 2, 3)\)
\(F(x,y,z) = e^{-xy}i + e^{xz}j + e^{yz}k\) at \((3, 2, 0)\)
[Hide Solution]
\(div \, F = 2 - 2e^{-6}\)
\(F(x,y,z) = xyz i + y j + zk\) at \((1, 2, 1)\)
\(F(x,y,z) = e^x \sin y i - e^x \cos y j \) at \((0, 0, 3)\)
\(div \, F = 0\)
For the following exercises, find the curl of F at the given point.
\(F(x,y,z) = i + j + k\) at \((2, -1, 3)\)
\(F(x,y,z) = xyz i + y j + zk\) at \((1, 2, 3)\)
[Hide Solution]
\(curl \, F = j - 3k\)
\(F(x,y,z) = e^{-xy}i + e^{xz}j + e^{yz}k\) at \((3, 2, 0)\)
\(F(x,y,z) = xyz i + y j + zk\) at \((1, 2, 1)\)
[Hide Solution]
\(curl \, F = 2j - k\)
\(F(x,y,z) = e^x \sin y i - e^x \cos y j \) at \((0, 0, 3)\)
Let \(F(x,y,z) = (3x^2 y + az) i + x^3 j + (3x + 3z^2) k\).
For what value of a is F conservative?
[Hide Solution]
\(a = 3\)
Given vector field \(\vecs{F}(x,y) = \dfrac{1}{x^2+y^2} (-y,x)\) on domain \(D = \dfrac{\mathbb{R}^2}{\{(0,0)\}} = \{(x,y) \in \mathbb{R}^2 |(x,y) \neq (0,0) \}\), is F conservative?
Given vector field \(\vecs{F}(x,y) = \dfrac{1}{x^2+y^2} (x,y)\) on domain \(D = \dfrac{\mathbb{R}^2}{\{(0,0)\}}\), is F conservative?
[Hide Solution]
F is conservative.
Find the work done by force field \(\vecs{F}(x,y) = e^{-y}i - xe^{-y}j\) in moving an object from P(0, 1) to Q(2, 0). Is the force field conservative?
Compute divergence \(F = (\sinh x) i + (\cosh y) j - xyz k\).
[Hide Solution]
\(div \, F = \cosh x + \sinh y - xy\)
Compute \(curl \, F = (\sinh x) i + (\cosh y) j - xyz k\).
For the following exercises, consider a rigid body that is rotating about the x-axis counterclockwise with constant angular velocity \(\omega = \langle a,b,c \rangle\). If P is a point in the body located at \(r = xi + yj + zk\), the velocity at P is given by vector field \(F = \omega \times r\).

Express F in terms of i, j, and k vectors.
[Hide Solution]
\((bz - cy)i(cx - az)j + (ay - bx)k\)
Find \(div \, F\).
Find \(curl \, F\)
[Hide Solution]
\(curl \, F = 2\omega\)
In the following exercises, suppose that \(\nabla \cdot F = 0\) and \(\nabla \cdot G = 0\).
Does \(F + G\) necessarily have zero divergence?
Does \(F \times G\) necessarily have zero divergence?
[Hide Solution]
\(F \times G\) does not have zero divergence.
In the following exercises, suppose a solid object in \(\mathbb{R}^3\) has a temperature distribution given by \(T(x,y,z)\). The heat flow vector field in the object is \(F = - k \nabla T\), where \(k > 0\) is a property of the material. The heat flow vector points in the direction opposite to that of the gradient, which is the direction of greatest temperature decrease. The divergence of the heat flow vector is \(\nabla \cdot F = -k \nabla \cdot \nabla T = - k \nabla^2 T\).
Compute the heat flow vector field.
Compute the divergence.
[Hide Solution]
\(\nabla \cdot F = -200 k [1 + 2(x^2 + y^2 + z^2)] e^{-x^2+y^2+z^2}\)
[T] Consider rotational velocity field \(v = \langle 0,10z, -10y \rangle\). If a paddlewheel is placed in plane \(x + y + z = 1\) with its axis normal to this plane, using a computer algebra system, calculate how fast the paddlewheel spins in revolutions per unit time.

Glossary
curl
the curl of vector field \(F = \langle P,Q,R \rangle\), denoted \(\nabla \times F\), is the “determinant” of the matrix \(\begin{vmatrix} i & j & k \nonumber \\ \dfrac{\partial}{\partial x} & \dfrac{\partial}{\partial y} & \dfrac{\partial}{\partial z} \nonumber \\ P & Q & R \end{vmatrix}\) and is given by the expression \((R_y - Q_z)i + (P_z - R_x ) j + (Q_x - P_y) k\); it measures the tendency of particles at a point to rotate about the axis that points in the direction of the curl at the point
divergence
the divergence of a vector field \(F = \langle P,Q,R\rangle \), denoted \(\nabla \times F\), is \(P_x + Q_y + R_z\); it measures the “outflowing-ness” of a vector field
16.6: Surface Integrals
For the following exercises, determine whether the statements are true or false.
If surface S is given by \(\{(x,y,z) : \, 0 \leq x \leq 1, \, 0 \leq y \leq 1, \, z = 10 \}\), then \[\iint_S f(x,y,z) \, dS = \int_0^1 \int_0^1 f (x,y,10) \, dx dy.\nonumber \]
[Hide Solution]
True
If surface S is given by \(\{(x,y,z) : \, 0 \leq x \leq 1, \, 0 \leq y \leq 1, \, z = x \}\), then \[\iint_S f(x,y,z) \, dS = \int_0^1 \int_0^1 f (x,y,x) \, dx dy.\nonumber \]
Surface
\(r = \langle v \, \cos u, \, v \, \sin u, \, v^2 \rangle, \, fpr \, 0 \leq u \leq \pi, \, 0 \leq v \leq 2\) is the same surface \(r = \langle \sqrt{v} \, \cos 2u, \, \sqrt{v} \, \sin 2u, \, v \rangle, \, for \, 0 \leq u \leq \dfrac{\pi}{2}, \, 0 \leq v \leq 4\).
[Hide Solution]
True
Given the standard parameterization of a sphere, normal vectors \(t_u \times t_v\) are outward normal vectors.
For the following exercises, find parametric descriptions for the following surfaces.
Plane \(3x - 2y + z = 2\)
[Hide Solution]
\(r(u,v) = \langle u, \, v, \, 2 - 3u + 2v \rangle \) for \(-\infty \leq u < \infty\) and \( - \infty \leq v < \infty\).
Paraboloid \(z = x^2 + y^2\), for \(0 \leq z \leq 9\).
Plane \(2x - 4y + 3z = 16\)
[Hide Solution]
\(r(u,v) = \langle u, \, v, \, \dfrac{1}{3} (16 - 2u + 4v) \rangle \) for \(|u| < \infty\) and \(|v| < \infty\).
The frustum of cone \(z^2 = x^2 + y^2\), for \(2 \leq z \leq 8\)
The portion of cylinder \(x^2 + y^2 = 9\) in the first octant, for \(0 \leq z \leq 3\)

[Hide Solution]
\(r(u,v) = \langle 3 \, \cos u, \, 3 \, \sin u, \, v \rangle \) for \(0 \leq u \leq \dfrac{\pi}{2}, \, 0 \leq v \leq 3\)
A cone with base radius r and height h, where r and h are positive constants
For the following exercises, use a computer algebra system to approximate the area of the following surfaces using a parametric description of the surface.
[T] Half cylinder \(\{ (r, \theta, z) : \, r = 4, \, 0 \leq \theta \leq \pi, \, 0 \leq z \leq 7 \}\)
[Hide Solution]
\(A = 87.9646\)
[T] Plane \(z = 10 - z - y\) above square \(|x| \leq 2, \, |y| \leq 2\)
For the following exercises, let S be the hemisphere \(x^2 + y^2 + z^2 = 4\), with \(z \geq 0\), and evaluate each surface integral, in the counterclockwise direction.
\[\iint_S z\, dS\nonumber \]
[Hide Solution]
\[\iint_S z \, dS = 8\pi\nonumber \]
\[\iint_S (x - 2y) \, dS\nonumber \]
\[\iint_S (x^2 + y^2) \, dS\nonumber \]
[Hide Solution]
\[\iint_S (x^2 + y^2) \, dS = 16 \pi\nonumber \]
For the following exercises, evaluate \[\int \int_S F \cdot N \, ds\nonumber \]for vector field F, where N is an outward normal vector to surface S.
\(F(x,y,z) = xi + 2yj = 3zk\), and S is that part of plane \(15x - 12y + 3z = 6\) that lies above unit square \(0 \leq x \leq 1, \, 0 \leq y \leq 1\).
\(\vecs{F}(x,y) = xi + yj\), and S is hemisphere \(z = \sqrt{1 - x^2 - y^2}\).
[Hide Solution]
\[\iint_S F \cdot N \, dS = \dfrac{4\pi}{3}\nonumber \]
\(F(x,y,z) = x^2 i + y^2 j + z^2 k\), and S is the portion of plane \(z = y + 1\) that lies inside cylinder \(x^2 + y^2 = 1\).

For the following exercises, approximate the mass of the homogeneous lamina that has the shape of given surface S. Round to four decimal places.
[T] S is surface \(z = 4 - x - 2y\), with \(z \geq 0, \, x \geq 0, \, y \geq 0; \, \xi = x.\)
[Hide Solution]
\(m \approx 13.0639\)
[T] S is surface \(z = x^2 + y^2\), with \(z \leq 1; \, \xi = z\).
[T] S is surface \(x^2 + y^2 + x^2 = 5\), with \(z \geq 1; \, \xi = \theta^2\).
[Hide Solution]
\(m \approx 228.5313\)
Evaluate \[\iint_S (y^2 zi + y^3j + xzk) \cdot dS,\nonumber \] where S is the surface of cube \(-1 \leq x \leq 1, \, -1 \leq y \leq 1\), and \(0 \leq z \leq 2\) in a counterclockwise direction.
Evaluate surface integral \[\iint_S gdS,\nonumber \] where \(g(x,y,z) = xz + 2x^2 - 3xy\) and S is the portion of plane \(2x - 3y + z = 6\) that lies over unit square R: \(0 \leq x \leq 1, \, 0 \leq y \leq 1\).
[Hide Solution]
\[\iint_S gdS = 3 \sqrt{4}\nonumber \]
Evaluate \[\iint_S (x + y + z)dS,\nonumber \] where S is the surface defined parametrically by \(R(u,v) = (2u + v)i + (u - 2v)j + (u + 3v)k\) for \(0 \leq u \leq 1\), and \(0 \leq v \leq 2\).

[T] Evaluate \[\iint_S (x - y^2 + z)dS,\nonumber \] where S is the surface defined parametrically by \(R(u,v) = u^2i + vj + uk\) for \(0 \leq u \leq 1, \, 0 \leq v \leq 1\).

[Hide Solution]
\[\iint_S (x^2 + y - z) \, dS \approx 0.9617\nonumber \]
[T] Evaluate where S is the surface defined by \(R(u,v) = ui - u^2j + vk, \, 0 \leq u \leq 2, \, 0 \leq v \leq 1\) for \(0 \leq u \leq 1, \, 0 \leq v \leq 2\).
Evaluate \[ \iint_S (x^2 + y^2) \, dS,\nonumber \] where S is the surface bounded above hemisphere \(z = \sqrt{1 - x^2 - y^2}\), and below by plane \(z = 0\).
[Hide Solution]
\[\iint_S (x^2 + y^2) \, dS = \dfrac{4\pi}{3}\nonumber \]
Evaluate \[ \iint_S (x^2 + y^2 + z^2) \, dS,\nonumber \] where S is the portion of plane that lies inside cylinder \(x^2 + y^2 = 1\).
[T] Evaluate \[\iint_S x^2 z dS,\nonumber \] where S is the portion of cone \(z^2 = x^2 + y^2\) that lies between planes \(z = 1\) and \(z = 4\).

[Hide Solution]
\[\iint_S x^2 zdS = \dfrac{1023\sqrt{2\pi}}{5}\nonumber \]
[T] Evaluate \[\iint_S (xz/y) \, dS,\nonumber \] where S is the portion of cylinder \(x = y^2\) that lies in the first octant between planes \(z = 0, \, z = 5\), and \(y = 4\).

[T] Evaluate \[\iint_S (z + y) \, dS,\nonumber \] where S is the part of the graph of \( z = \sqrt{1 - x^2}\) in the first octant between the xz-plane and plane \(y = 3\).

[Hide Solution]
\[\iint_S (z + y) \, dS \approx 10.1\nonumber \]
Evaluate \[\iint_S xyz\, dS\nonumber \] if S is the part of plane \(z = x + y\) that lies over the triangular region in the xy-plane with vertices (0, 0, 0), (1, 0, 0), and (0, 2, 0).
Find the mass of a lamina of density \(\xi (x,y,z) = z\) in the shape of hemisphere \(z = (a^2 - x^2 - y^2)^{1/2}\).
[Hide Solution]
\(m = \pi a^3\)
Compute \[\int \int_S F \cdot N \, dS,\nonumber \] where \(F(x,y,z) = xi - 5yj + 4zk\) and N is an outward normal vector S, where S is the union of two squares \(S_1\) : \(x = 0, \, 0 \leq y \leq 1, \, 0 \leq z \leq 1\) and \(S_2 \, : \, x = 0, \, 0 \leq x \leq 1, \, 0 \leq y \leq 1\).

Compute \[\int \int_S F \cdot N \, dS,\nonumber \] where \(F(x,y,z) = xyi + zj + (x + y)k\) and N is an outward normal vector S, where S is the triangular region cut off from plane \(x + y + z = 1\) by the positive coordinate axes.
[Hide Solution]
\[\iint_S F \cdot N \, dS = \dfrac{13}{24}\nonumber \]
Compute \[\int \int_S F \cdot N \, dS,\nonumber \] where \(F(x,y,z) = 2yzi + (tan^{-1}xz)j + e^{xy}k\) and N is an outward normal vector S, where S is the surface of sphere \(x^2 + y^2 + z^2 = 1\).
Compute \[\int \int_S F \cdot N \, dS,\nonumber \] where \(F(x,y,z) = xyzi + xyzj + xyzk\) and N is an outward normal vector S, where S is the surface of the five faces of the unit cube \(0 \leq x \leq 1, \, 0 \leq y \leq 1, \, 0 \leq z \leq 1\) missing \(z = 0\).
[Hide Solution]
\[\iint_S F \cdot N \, dS = \dfrac{3}{4}\nonumber \]
For the following exercises, express the surface integral as an iterated double integral by using a projection on S on the yz-plane.
\[\iint_S xy^2 z^3 \, dS;\nonumber \] S is the first-octant portion of plane \(2x + 3y + 4z = 12\).
\[\iint_S (x^2 - 2y + z \, dS;\nonumber \] S is the portion of the graph of \(4x + y = 8\) bounded by the coordinate planes and plane \(z = 6\).
[Hide Solution]
\[\int_0^8 \int_0^6 \left( 4 - 3y + \dfrac{1}{16} y^2 + z \right) \left(\dfrac{1}{4} \sqrt{17} \right) \, dz dy\nonumber \]
For the following exercises, express the surface integral as an iterated double integral by using a projection on S on the xz-plane
\[\iint_S xy^2z^3 \, dS;\nonumber \] S is the first-octant portion of plane \(2x + 3y + 4z = 12\).
\[\iint_S (x^2 - 2y + z) \, dS;\nonumber \] is the portion of the graph of \(4x + y = 8\) bounded by the coordinate planes and plane \(z = 6\).
[Hide Solution]
\[\int_0^2 \int_0^6 [x^2 - 2 (8 - 4x) + z] \sqrt{17} \, dz dx\nonumber \]
Evaluate surface integral \[\iint_S yz \, dS,\nonumber \] where S is the first-octant part of plane \(x + y + z = \lambda\), where \(\lambda\) is a positive constant.
Evaluate surface integral \[\iint_S (x^2 z + y^2 z) \, dS,\nonumber \] where S is hemisphere \(x^2 + y^2 + z^2 = a^2, \, z \geq 0.\)
[Hide Solution]
\[\iint_S (x^2 z + y^2 z) \, dS = \dfrac{\pi a^5}{2}\nonumber \]
Evaluate surface integral \[\iint_S zdA,\nonumber \] where S is surface \(z = \sqrt{x^2 + y^2}, \, 0 \leq z \leq 2\).
Evaluate surface integral \[\iint_S x^2 yz \, dS,\nonumber \] where S is the part of plane \(z = 1 + 2x + 3y\) that lies above rectangle \(0 \leq x \leq 3\) and \(0 \leq y \leq 2\).
[Hide Solution]
\[\iint_S x^2 yz \, dS = 171 \sqrt{14}\nonumber \]
Evaluate surface integral \[\iint_S yz \, dS,\nonumber \] where S is plane \(x + y + z = 1\) that lies in the first octant.
Evaluate surface integral \[\iint_S yz \, dS,\nonumber \] where S is the part of plane \(z = y + 3\) that lies inside cylinder \(x^2 + y^2 = 1\).
[Hide Solution]
\[\iint_S yz \, dS = \dfrac{\sqrt{2}\pi}{4}\nonumber \]
For the following exercises, use geometric reasoning to evaluate the given surface integrals.
\[\iint_S \sqrt{x^2 + y^2 + z^2} \, dS,\nonumber \] where S is surface \(x^2 + y^2 + z^2 = 4, \, z \geq 0\)
\[\iint_S (xi + yj) \cdot dS,\nonumber \] where S is surface \(x^2 + y^2 = 4, \, 1 \leq z \leq 3\), oriented with unit normal vectors pointing outward
[Hide Solution]
\[\iint_S (xi + yj) \cdot dS = 16 \pi\nonumber \]
\[\iint_S (zk) \cdot dS,\nonumber \] where S is disc \(x^2 + y^2 \leq 9\) on plane \(z = 4\) oriented with unit normal vectors pointing upward
A lamina has the shape of a portion of sphere \(x^2 + y^2 + z^2 = a^2\) that lies within cone \(z = \sqrt{x^2 + y^2}\). Let S be the spherical shell centered at the origin with radius a, and let C be the right circular cone with a vertex at the origin and an axis of symmetry that coincides with the z-axis. Determine the mass of the lamina if \(\delta(x,y,z) = x^2 y^2 z\).

[Hide Solution]
\(m = \dfrac{\pi a^7}{192}\)
A lamina has the shape of a portion of sphere \(x^2 + y^2 + z^2 = a^2\) that lies within cone \(z = \sqrt{x^2 + y^2}\). Let S be the spherical shell centered at the origin with radius a, and let C be the right circular cone with a vertex at the origin and an axis of symmetry that coincides with the z-axis. Suppose the vertex angle of the cone is \(\phi_0\), with \(0 \leq \phi_0 < \dfrac{\pi}{2}\). Determine the mass of that portion of the shape enclosed in the intersection of S and C. Assume \(\delta(x,y,z) = x^2y^2z.\)

A paper cup has the shape of an inverted right circular cone of height 6 in. and radius of top 3 in. If the cup is full of water weighing \(62.5 \, lb/ft^3\), find the total force exerted by the water on the inside surface of the cup.
[Hide Solution]
\(F \approx 4.57 \, lb\)
For the following exercises, the heat flow vector field for conducting objects i \(F = - k\nabla T\), where \(T(x,y,z)\) is the temperature in the object and \(k > 0\) is a constant that depends on the material. Find the outward flux of F across the following surfaces S for the given temperature distributions and assume \(k = 1\).
\(T(x,y,z) = 100 e^{-x-y}\); S consists of the faces of cube \(|x| \leq 1, \, |y| \leq 1, \, |z| \leq 1\).
\(T(x,y,z) = - \ln (x^2 + y^2 + z^2)\); S is sphere \(x^2 + y^2 + z^2 = a^2\).
[Hide Solution]
\(8\pi a\)
For the following exercises, consider the radial fields \(F = \dfrac{\langle x,y,z \rangle}{(x^2+y^2+z^2)^{\dfrac{p}{2}}} = \dfrac{r}{|r|^p}\), where p is a real number. Let S consist of spheres A and B centered at the origin with radii \(0 < a < b\). The total outward flux across S consists of the outward flux across the outer sphere B less the flux into S across inner sphere A.

Find the total flux across S with \(p = 0\).
Show that for \(p = 3\) the flux across S is independent of a and b.
[Hide Solution]
The net flux is zero.
16.7: Stokes’ Theorem
For the following exercises, without using Stokes’ theorem, calculate directly both the flux of \(curl \, F \cdot N\) over the given surface and the circulation integral around its boundary, assuming all are oriented clockwise.
\(F(x,y,z) = y^2i + z^2j + x^2k\); S is the first-octant portion of plane \(x + y + z = 1\).
\(F(x,y,z) = zi + xj + yk\); S is hemisphere \(z = (a^2 - x^2 - y^2)^{1/2}\).
[Hide Solution]
\[\iint_S (curl \, F \cdot N) \, dS = \pi a^2\nonumber \]
\(F(x,y,z) = y^2i + 2xj + 5k\); S is hemisphere \(z = (4 - x^2 - y^2)^{1/2}\).
\(F(x,y,z) = zi + 2xj + 3yk\); S is upper hemisphere \(z = \sqrt{9 - x^2 - y^2}\).
[Hide Solution]
\[\iint_S (curl \, F \cdot N) \, dS = 18 \pi\nonumber \]
\(F(x,y,z) = (x + 2z)i + (y - x)j + (z - y)k\); S is a triangular region with vertices (3, 0, 0), (0, 3/2, 0), and (0, 0, 3).
\(F(x,y,z) = 2yi + 6zj + 3xk\); S is a portion of paraboloid \(z = 4 - x^2 - y^2\) and is above the xy-plane.
[Hide Solution]
\[\iint_S (curl \, F \cdot N) \, dS = -8 \pi\nonumber \]
For the following exercises, use Stokes’ theorem to evaluate
\[\iint_S (curl \, F \cdot N) \, dS\nonumber \] for the vector fields and surface.
\(F(x,y,z) = xyi - zj\) and S is the surface of the cube \(0 \leq x \leq 1, \, 0 \leq y \leq 1, \, 0 \leq z \leq 1\), except for the face where \(z = 0\) and using the outward unit normal vector.
\(F(x,y,z) = xyi + x^2 j + z^2 k\); and C is the intersection of paraboloid \(z = x^2 + y^2\) and plane \(z = y\), and using the outward normal vector.
\[\iint_S (curl \, F \cdot N) \, dS = 0\nonumber \]
\(F(x,y,z) = 4yi + z j + 2y k\); and C is the intersection of sphere \(x^2 + y^2 + z^2 = 4\) with plane \(z = 0\), and using the outward normal vector.
Use Stokes’ theorem to evaluate \[\int_C [2xy^2z \, dx + 2x^2yz \, dy + (x^2y^2 - 2z) \, dz],\nonumber \] where C is the curve given by \(x = \cos t, \, y = \sin t, \, 0 \leq t \leq 2\pi\), traversed in the direction of increasing t.

[Hide Solution]
\[\int_C F \cdot dS = 0\nonumber \]
[T] Use a computer algebraic system (CAS) and Stokes’ theorem to approximate line integral \[\int_C (y \, dx + z \, dy + x \, dz),\nonumber \] where C is the intersection of plane \(x + y = 2\) and surface \(x^2 + y^2 + z^2 = 2(x + y)\), traversed counterclockwise viewed from the origin.
[T] Use a CAS and Stokes’ theorem to approximate line integral \[\int_C (3y\, dx + 2z \, dy - 5x \, dz),\nonumber \] where C is the intersection of the xy-plane and hemisphere \(z = \sqrt{1 - x^2 - y^2}\), traversed counterclockwise viewed from the top—that is, from the positive z-axis toward the xy-plane.
[Hide Solution]
\[\int_C F \cdot dS = - 9.4248\nonumber \]
[T] Use a CAS and Stokes’ theorem to approximate line integral \[ \int_C [(1 + y) \, z dx + (1 + z) x dy + (1 + x) y dz],\nonumber \] where C is a triangle with vertices \((1,0,0), \, (0,1,0)\), and \((0,0,1)\) oriented counterclockwise.
Use Stokes’ theorem to evaluate \[\iint_S curl \, F \cdot dS,\nonumber \] where \(F(x,y,z) = e^{xy} cos \, zi + x^2 zj + xyk\), and S is half of sphere \(x = \sqrt{1 - y^2 - z^2}\), oriented out toward the positive x-axis.
[Hide Solution]
\[\iint_S F \cdot dS = 0\nonumber \]
[T] Use a CAS and Stokes’ theorem to evaluate \[\iint_S (curl \, F \cdot N) \, dS,\nonumber \] where \(F(x,y,z) = x^2 yi + xy^2 j + z^3 k\) and C is the curve of the intersection of plane \(3x + 2y + z = 6\) and cylinder \(x^2 + y^2 = 4\), oriented clockwise when viewed from above.
[T] Use a CAS and Stokes’ theorem to evaluate \[\iint_S curl \, F \cdot dS,\nonumber \] where \(F(x,y,z) = \left( \sin(y + z) - yx^2 - \dfrac{y^3}{3}\right)i + x \, \cos (y + z) j + \cos (2y) \, k\) and S consists of the top and the four sides but not the bottom of the cube with vertices \((\pm 1, \, \pm1, \, \pm1)\), oriented outward.
[Hide Solution]
\[\iint_S curl \, F \cdot dS = 2.6667\nonumber \]
[T] Use a CAS and Stokes’ theorem to evaluate \[\iint_S curl \, F \cdot dS,\nonumber \] where \(F(x,y,z) = z^2i + 3xyj + x^3y^3k\) and S is the top part of \(z = 5 - x^2 - y^2\) above plane \(z = 1\) and S is oriented upward.
Use Stokes’ theorem to evaluate \[\iint_S (curl \, F \cdot N) dS,\nonumber \] where \(F(x,y,z) = z^2i + y^2j + xk\) and S is a triangle with vertices (1, 0, 0), (0, 1, 0) and (0, 0, 1) with counterclockwise orientation.
[Hide Solution]
\[\iint_S (curl \, F \cdot N)dS = -\dfrac{1}{6}\nonumber \]
Use Stokes’ theorem to evaluate line integral \[\int_C (z \, dx + x \, dy + y \, dz),\nonumber \] where C is a triangle with vertices (3, 0, 0), (0, 0, 2), and (0, 6, 0) traversed in the given order.
Use Stokes’ theorem to evaluate \[\int_C \left(\dfrac{1}{2} y^2 \, dx + z \, dy + x \, dz \right),\nonumber \] where C is the curve of intersection of plane \(x + z = 1\) and ellipsoid \(x^2 + 2y^2 + z^2 = 1\), oriented clockwise from the origin.

[Hide Solution]
\[\int_C \left(\dfrac{1}{2} y^2 \, dx + z \, dy + x \, dz \right) = - \dfrac{\pi}{4}\nonumber \]
Use Stokes’ theorem to evaluate \[\iint_S (curl \, F \cdot N) dS,\nonumber \] where \(F(x,y,z) = xi + y^2j + ze^{xy}k\) and S is the part of surface \(z = 1 - x^2 - 2y^2\) with \(z \geq 0\), oriented counterclockwise.
Use Stokes’ theorem for vector field \(F(x,y,z) = zi + 3xj + 2zk\) where S is surface \(z = 1 - x^2 - 2y^2, \, z \geq 0\), C is boundary circle \(x^2 + y^2 = 1\), and S is oriented in the positive z-direction.
[Hide Solution]
\[\iint_S (curl \, F \cdot N)dS = -3\pi]
Use Stokes’ theorem for vector field \(F(x,y,z) = - \dfrac{3}{2} y^2 i - 2 xyj + yzk\), where S is that part of the surface of plane \(x + y + z = 1\) contained within triangle C with vertices (1, 0, 0), (0, 1, 0), and (0, 0, 1), traversed counterclockwise as viewed from above.
A certain closed path C in plane \(2x + 2y + z = 1\) is known to project onto unit circle \(x^2 + y^2 = 1\) in the xy-plane. Let c be a constant and let \(R(x,y,z) = xi + yj + zk\). Use Stokes’ theorem to evaluate \[\int_C(ck \times R) \cdot dS.\nonumber \]
[Hide Solution]
\[\int_C (ck \times R) \cdot dS = 2\pi c\nonumber \]
Use Stokes’ theorem and let C be the boundary of surface \(z = x^2 + y^2\) with \(0 \leq x \leq 2\) and \(0 \leq y \leq 1\) oriented with upward facing normal. Define
\(F(x,y,z) = [\sin (x^3) + xz] i + (x - yz)j + \cos (z^4) k\) and evaluate \(\int_C F \cdot dS\).
Let S be hemisphere \(x^2 + y^2 + z^2 = 4\) with \(z \geq 0\), oriented upward. Let \(F(x,y,z) = x^2 e^{yz}i + y^2 e^{xz} j + z^2 e^{xy}k\) be a vector field. Use Stokes’ theorem to evaluate \[\iint_S curl \, F \cdot dS.\nonumber \]
[Hide Solution]
\[\iint_S curl \, F \cdot dS = 0\nonumber \]
Let \(F(x,y,z) = xyi + (e^{z^2} + y)j + (x + y)k\) and let S be the graph of function \(y = \dfrac{x^2}{9} + \dfrac{z^2}{9} - 1\) with \(z \leq 0\) oriented so that the normal vector S has a positive y component. Use Stokes’ theorem to compute integral \[\iint_S curl \, F \cdot dS.\nonumber \]
Use Stokes’ theorem to evaluate \[ \oint F \cdot dS,\nonumber \] where \(F(x,y,z) = yi + zj + xk\) and C is a triangle with vertices (0, 0, 0), (2, 0, 0) and \(0,-2,2)\) oriented counterclockwise when viewed from above.
[Hide Solution]
\[ \oint F \cdot dS = -4\nonumber \]
Use the surface integral in Stokes’ theorem to calculate the circulation of field F, \(F(x,y,z) = x^2y^3 i + j + zk\) around C, which is the intersection of cylinder \(x^2 + y^2 = 4\) and hemisphere \(x^2 + y^2 + z^2 = 16, \, z \geq 0\), oriented counterclockwise when viewed from above.

Use Stokes’ theorem to compute \[\iint_S curl \, F \cdot dS.\nonumber \] where \(F(x,y,z) = i + xy^2j + xy^2 k\) and S is a part of plane \(y + z = 2\) inside cylinder \(x^2 + y^2 = 1\) and oriented counterclockwise.

[Hide Solution]
\[\iint_S curl \, F \cdot dS = 0\nonumber \]
Use Stokes’ theorem to evaluate \[\iint_S curl \, F \cdot dS,\nonumber \] where \(F(x,y,z) = -y^2 i + xj + z^2k\) and S is the part of plane \(x + y + z = 1\) in the positive octant and oriented counterclockwise \(x \geq 0, \, y \geq 0, \, z \geq 0\).
Let \(F(x,y,z) = xyi + 2zj - 2yk\) and let C be the intersection of plane \(x + z = 5\) and cylinder \(x^2 + y^2 = 9\), which is oriented counterclockwise when viewed from the top. Compute the line integral of F over C using Stokes’ theorem.
[Hide Solution]
\[\iint_S curl \, F \cdot dS = -36 \pi\nonumber \]
[T] Use a CAS and let \(F(x,y,z) = xy^2i + (yz - x)j + e^{yxz}k\). Use Stokes’ theorem to compute the surface integral of curl F over surface S with inward orientation consisting of cube \([0,1] \times [0,1] \times [0,1]\) with the right side missing.
Let S be ellipsoid \(\dfrac{x^2}{4} + \dfrac{y^2}{9} + z^2 = 1\) oriented counterclockwise and let F be a vector field with component functions that have continuous partial derivatives.
[Hide Solution]
\[\iint_S curl \, F \cdot N = 0\nonumber \]
Let S be the part of paraboloid \(z = 9 - x^2 - y^2\) with \(z \geq 0\). Verify Stokes’ theorem for vector field \(F(x,y,z) = 3zi + 4xj + 2yk\).
[T] Use a CAS and Stokes’ theorem to evaluate \[\oint F \cdot dS,\nonumber \] if \(F(x,y,z) = (3z - \sin x) i + (x^2 + e^y) j + (y^3 - \cos z) k\), where C is the curve given by \(x = \cos t, \, y = \sin t, \, z = 1; \, 0 \leq t \leq 2\pi\).
[Hide Solution]
\[\oint_C F \cdot dr = 0\nonumber \]
[T] Use a CAS and Stokes’ theorem to evaluate \(F(x,y,z) = 2yi + e^zj - arctan \, xk\) with S as a portion of paraboloid \(z = 4 - x^2 - y^2\) cut off by the xy-plane oriented counterclockwise.
[T] Use a CAS to evaluate \[\iint_S curl (F) \cdot dS,\nonumber \] where \(F(x,y,z) = 2zi + 3xj + 5yk\) and S is the surface parametrically by \(r(r,\theta) = r \, \cos \theta i + r \, \sin \theta j + (4 - r^2) k \, (0 \leq \theta \leq 2\pi, \, 0 \leq r \leq 3)\).
[Hide Solution]
\[\iint_S curl (F) \cdot dS = 84.8230\nonumber \]
Let S be paraboloid \(z = a (1 - x^2 - y^2)\), for \(z \geq 0\), where \(a > 0\) is a real number. Let \(F(x,y,z) = \langle x - y, \, y + z, \, z - x \rangle\). For what value(s) of a (if any) does \[\iint_S (\nabla \times F) \cdot n \, dS\nonumber \] have its maximum value?
For the following application exercises, the goal is to evaluate \[A = \iint_S (\nabla \times F) \cdot n \, dS,\nonumber \] where \(F = \langle xz, \, -xz, \, xy \rangle\) and S is the upper half of ellipsoid \(x^2 + y^2 + 8z^2 = 1\), where \(z \geq 0\).
Evaluate a surface integral over a more convenient surface to find the value of A.
[Hide Solution]
\[A = \iint_S (\nabla \times F) \cdot n \, dS = 0\nonumber \]
Evaluate A using a line integral.
Take paraboloid \(z = x^2 + y^2\), for \(0 \leq z \leq 4\), and slice it with plane \(y = 0\). Let S be the surface that remains for \(y \geq 0\), including the planar surface in the xz-plane. Let C be the semicircle and line segment that bounded the cap of S in plane \(z = 4\) with counterclockwise orientation. Let \(F = \langle 2z + y, \, 2x + z, \, 2y + x \rangle\). Evaluate \[\iint_S (\nabla \times F) \cdot n \, dS.\nonumber \]

[Hide Solution]
\[\iint_S (\nabla \times F) \cdot n \, dS = 2\pi\nonumber \]
For the following exercises, let S be the disk enclosed by curve \(C \, : \, r(t) = \langle \cos \varphi \, \cos t, \, \sin t, \, \sin \varphi \, \cos t \rangle\), for \(0 \leq t \leq 2\pi\), where \(0 \leq \varphi \leq \dfrac{\pi}{2}\) is a fixed angle.
What is the length of C in terms of \(\varphi\)?
What is the circulation of C of vector field \(F = \langle -y, \, -z, \, x \rangle\) as a function of \(\varphi\)?
[Hide Solution]
\(C = \pi (\cos \varphi - \sin \varphi)\)
For what value of \(\varphi\) is the circulation a maximum?
Circle C in plane \(x + y + z = 8\) has radius 4 and center (2, 3, 3). Evaluate \[\oint_C F \cdot dr\nonumber \] for \(F = \langle 0, \, -z, \, 2y \rangle\), where C has a counterclockwise orientation when viewed from above.
[Hide Solution]
\[\oint_C F \cdot dr = 48 \pi\nonumber \]
Velocity field \(v = \langle 0, \, 1 -x^2, \, 0 \rangle \), for \(|x| \leq 1\) and \(|z| \leq 1\), represents a horizontal flow in the y-direction. Compute the curl of v in a clockwise rotation.
Evaluate integral \[ \iint_S (\nabla \times F) \cdot n \, dS,\nonumber \] where \(F = - xzi + yzj + xye^z k\) and S is the cap of paraboloid \(z = 5 - x^2 - y^2\) above plane \(z = 3\), and n points in the positive z-direction on S.
[Hide Solution]
\[ \iint_S (\nabla \times F) \cdot n = 0\nonumber \]
For the following exercises, use Stokes’ theorem to find the circulation of the following vector fields around any smooth, simple closed curve C.
\(F = \nabla (x \, \sin ye^z)\)
\(F = \langle y^2z^3, \, z2xyz^3, 3xy^2z^2 \rangle \)
[Hide Solution]
0
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.


